Similar presentations:
Аналитическая геометрия
1. Аналитическая геометрия
Занятие №13Фролов Игорь Владимирович
IVFrolov@mephi.ru
2. Матрицы
Матрицей порядка m n называют прямоугольную таблицучисел (вещественных или комплексных), содержащую m
строк и n столбцов.
Если число строк матрицы равно числу столбцов, то матрица
называется квадратной, а число ее строк - порядком матрицы.
3. Перестановки
Всякое расположение чисел 1, 2,..., n в некотором определенномпорядке называется перестановкой из n чисел
Обозначим N(i1,i2,... in) число беспорядков (инверсий) в
перестановке (i1,i2,... in) т.е. таких пар чисел в ней, в которых большее
число стоит впереди.
Например, в перестановке (4, 2,1,3) беспорядки образуют пары:
(4,2), (4,1), (4,3), (2,1) и N (4, 2, 1, 3) =4.
Перестановка является четной.
4. Определители
Пусть А - квадратная матрица порядка n. Определителем этойматрицы называется алгебраическая сумма всевозможных
произведений из n элементов, взятых по одному из каждого столбца и
каждой строки матрицы А.
Во всяком таком произведении множители располагают в порядке
следования столбцов.
Со знаком плюс берутся те произведения, у которых перестановка
первых индексов четная,
со знаком минус — те, у которых перестановка нечетная.
5. Свойства определителя
I. Если все элементы какой-либо строки (столбца) определителя равнынулю, то он равен нулю.
II. Если переставить две строки (два столбца) определителя, то он
изменит знак.
III. Если две строки (два столбца) определителя одинаковы, то он равен
нулю.
IV. Если две строки (два столбца) определителя пропорциональны, то он
равен нулю.
V. Если все элементы какой-либо строки (столбца) определителя
умножить на некоторое число K, то сам определитель умножится на K.
VI. Если все элементы i-й строки определителя представлены в виде
aij=bj+cj то определитель равен сумме двух определителей, у которых все
строки, кроме i-й, прежние, а в i-й строке в первом определителе стоят
элементы bj во втором — элементы cj.
Аналогичное свойство справедливо и для столбцов.
VII. Определитель не изменится, если к элементам одной его строки
(столбца) прибавить соответствующие элементы другой строки (столбца),
умноженные на одно и то же число.
6. Вычисление определителя Рекуррентная формула 1
a11a
A 21
...
an1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
Минором Мij элемента аij матрицы A порядка n называется
определитель матрицы (n — 1)-го порядка, получающийся из А
вычеркиванием i-й строки и j-го столбца.
формула разложения
определителя по i-й строке
формула разложения
определителя по j-му столбцу
7. Вычисление определителя Рекуррентная формула 2
a11a
A 21
...
an1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
Метод элементарных преобразований столбцов
Выделяем строку i, в котором мы хотим получить (n —1) нулей.
Выделяем элемент aij , который мы хотим оставить ненулевым.
Из каждого столбца k≠j вычитаем линейную комбинацию
оставшихся столбцов так чтобы коэффициент в позиции ik
обращался в 0
Определитель будет равен (-1)i+jaij Mij
Аналогичная процедура может быть сформулирована для строк
8.
9.
10.
11.
33 5
8
3
3 5
8
3
3 5
14
3
2
4
6
3
2
4
6
3
2
12
2
5 7
5
2
5 7
5
2
5 7
9
4
3
6
1
0
0
2
1
0
0
0 2
1
4
5
3 5
14
2
12 2
4
5 7
9
3 1
0
4
5 3 21
3 21
2
4
0
1 4
0 9
18
12. Операции над матрицами. Линейные операции
•Операция сложения - возможна только для матриц одинаковойразмерности
Складываются элементы матрицы с одинаковыми индексами
•Операция умножения на число – для любых матриц.
Все элементы матрицы умножаются на одно число
13. Операции над матрицами. Транспонирование матриц
При транспонировании строки и столбцы матрицыменяются местами
Меняется размерность неквадратной матрицы:
m n→ n m
14. Операции над матрицами. Умножение матриц
Умножение матриц – возможно, если число столбцов матрицы Аравно числу строк матрицы В.
Размерность матрицы: m n ∙ n p → m p
В общем случае коммутативность нарушается AB ≠ BA
15.
Умножается каждая строка матрицы слева на каждый столбец матрицысправа
Обозначим:
r1 r2 – строки матрицы слева
с1 с2 – столбцы матрицы справа
(r1c1) : c11 a b a b
(r 2c1) : c21 c d c d
a b
C
c d
c1 c 2
r1 a
b
r2 c
d
(r1c2) : c12 a b a b
(r 2c 2) : c22 c d c d
a b
c d
16.
с11 5 3 8 4 4 9 11с21 6 3 9 4 5 9 9
с31 4 3 7 4 3 9 13
с12 5 2 8 1 4 6 22
с22 6 2 9 1 5 6 27
с32 4 2 7 1 3 6 17
с13 5 5 8 3 4 5 29
с23 6 5 9 3 5 5 32
с33 4 5 7 3 3 5 26
11 22 29
С 9 27 32
13 17 26
17.
4 3 28 7 93 2 28 3 93 17 5 38 7 126 2 38 3 126 1
4 3 10 9
7 5 14 12
4 10 3 14 4 9 3 12 2 0
7
10
5
14
7
9
5
12
0
3
18.
7991 2 1 2 1 1 2 3 2 1 2 4 5 6
3
4
3
4
3
1
4
3
2
3
4
4
9 10
1 2 5 6 1 5 2 9 1 6 2 10 13 14
3
4
9
10
3
5
4
9
3
6
4
10
21 22
cos
sin
sin cos
cos sin
sin cos 2
cos sin 2
sin 2
cos 2
802
cos k
sin k
sin k cos
cos k sin
sin cos(k 1)
cos sin(k 1)
sin(k 1)
cos(k 1)
19.
( A AT )B
2
( A AT )
C
2
20. Операции над матрицами. Единичная матрица. Обратная матрица
Диагональная матрица (квадратная), у которой вседиагональные элементы равны 1, называется единичной
где δij - символ Кронекера
AE=EA=A
Пусть А — квадратная матрица. Матрица В той же размерности
называется обратной к А и обозначается В = А-1, если
21. Операции над матрицами. Обращение матриц
a11a
A 21
...
an1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
Минором Мij элемента аij матрицы A порядка n называется
определитель матрицы (n — 1)-го порядка, получающийся из А
вычеркиванием i-й строки и j-го столбца.
Алгебраическим дополнением Аij элемента аij называется
число
Если выполнено условие det(A)≠0 матрица A имеет обратную
B=A-1 и ее элементы рассчитываются по формуле
22. Операции над матрицами. Обращение матрицы
Процедура нахождения обратной матрицы: .1. Составляем матрицу А* = (а *ij) ‚ элементами
которой являются алгебраические дополнения
элементов исходной матрицы
2. Транспонируем ее: А*T
3. Умножаем на (detA)-1
В результате получаем обратную матрицу:
A-1=A*T/det(A)
23.
det A 21 20 1A11 7
A21 4
A12 5
A22 3
7 5
A*
4 3
7 4
A*T
5 3
1 7 4 7 4
A 1
1 5 3 5 3
7 4 3 4 1 0
1
A A
E
5
3
5
7
0
1
24.
A113
3
5 1
2
1 1
5
3 5
2 1
2 3
3 5
7
1
3 5
2 3
det( A) a11 A11 a12 A12 a13 A13 3 8 4 5 5 1 1
5
18
3 4
3 4
29
11
3
3 1
A23
A33
5
3 1
A32
A13
4
4 5
A12
A22
8
5 1
A21
A31
1
3
1
8
A* 29
11
8
A*T 5
1
8
A 1 5
1
1
18 3
7 1
29 11
18 7
3 1
29 11
18 7
3 1
5
25.
AXB CX A 1CB 1
2 1
A
5
3
1 8 6
B 1
2 7 5
1
26.
AX B1
X A B
det(A)=4
1 0 1
A 2 1 0
1 1 1
1 2 3
A* 1 2 1
1 2 1
1 1 1
A*T 2 2 2
3 1 1
1 1 1
1
A 1 2 2 2
4
3 1 1
10
1
X 26
4
4
1
B 3
6
27.
Операции над матрицами.2-й способ нахождения обратной матрицы.
Составляем матрицу n 2n :
(A E)
В нашем распоряжении элементарные операции со строками
1) перестановка строк;
2) умножение (деление) всей строки на одно и то же число не
равное 0
3) прибавление к одной из строк любой другой, умноженной на.
произвольное число.
Наша цель — получить единичную матрицу на месте А,
28.
3 4 5 1 0 0 3 4 5 1 0 0 1 1 4 1 1 0( A | E ) 2 3 1 0 1 0 ~ 2 3 1 0 1 0 ~ 2 3 1 4 0 1 0
3 5 1 0 0 1 0 1 6 1 0 1 0 1 6 1 0 1
1 1 4 1 1 0 1 1 4 1 1 0
~ 0 1 7 2 3 0 ~ 0 1 7 2 3 0
0 1 6 1 0 1 0 0 1 1 3 1
1 1 0 3 11 4 1 0 0 8 29 11 1 0 0 8 29 11
~ 0 1 0 5 18 7 ~ 0 1 0 5 18 7 ~ 0 1 0 5 18 7
0 0 1 1 3 1 0 0 1 1 3
1 0 0 1 1 3 1
29.
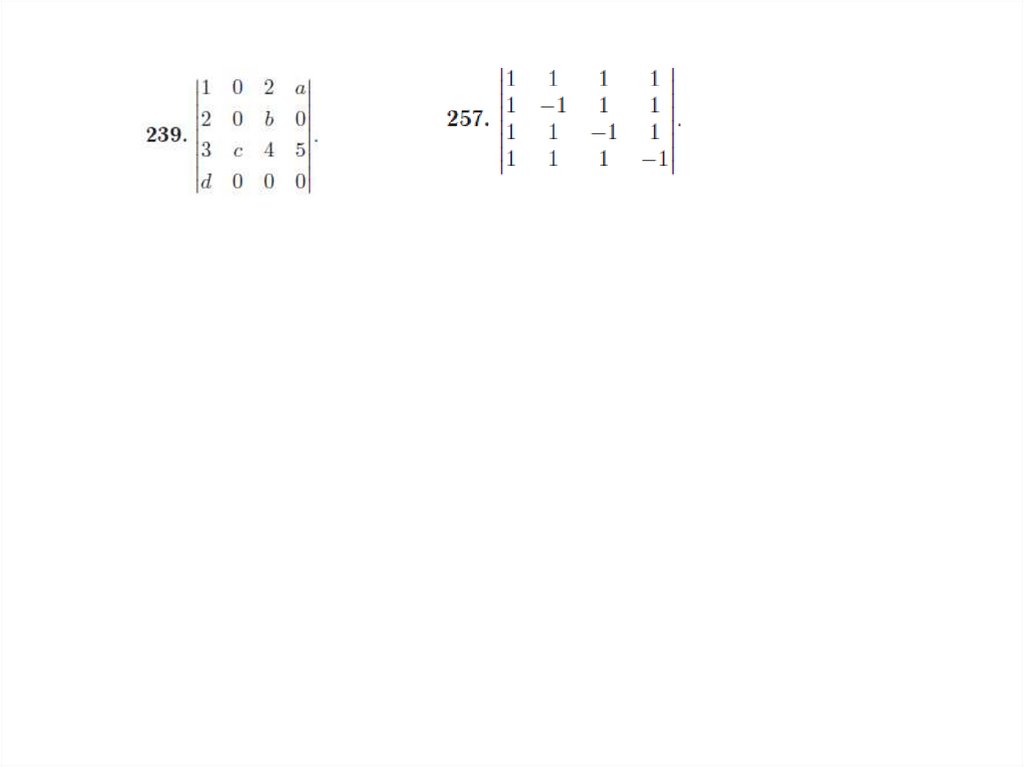
На дом:П. 788,790,792,797,800,804,808,828,836,838,840,862














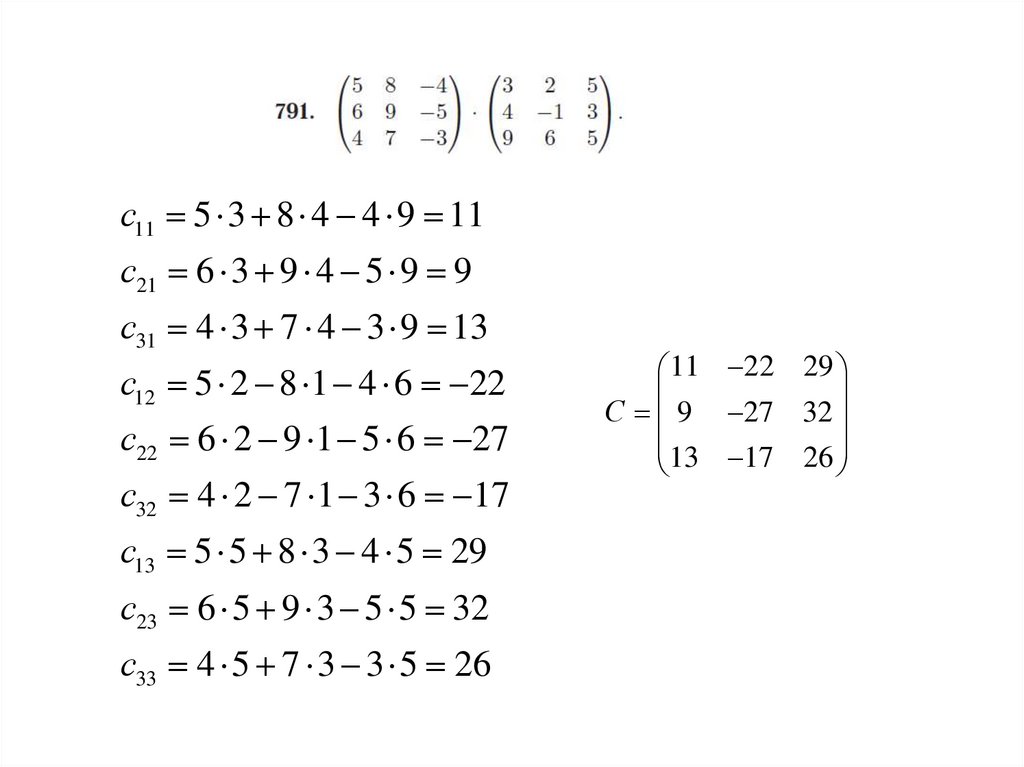








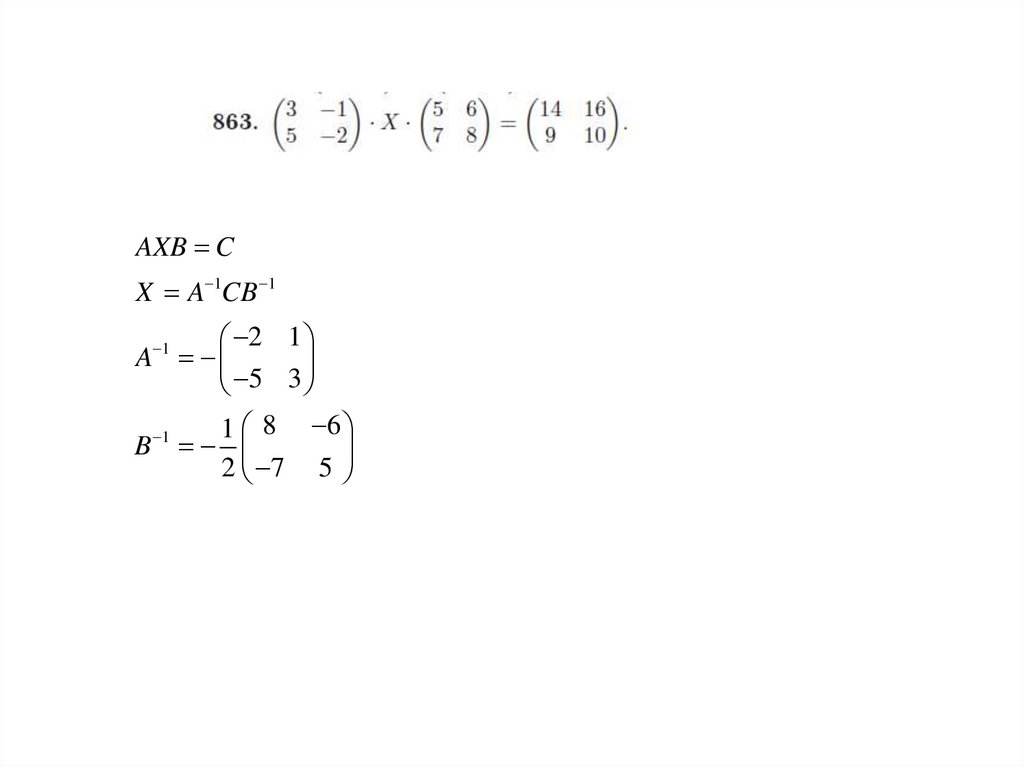
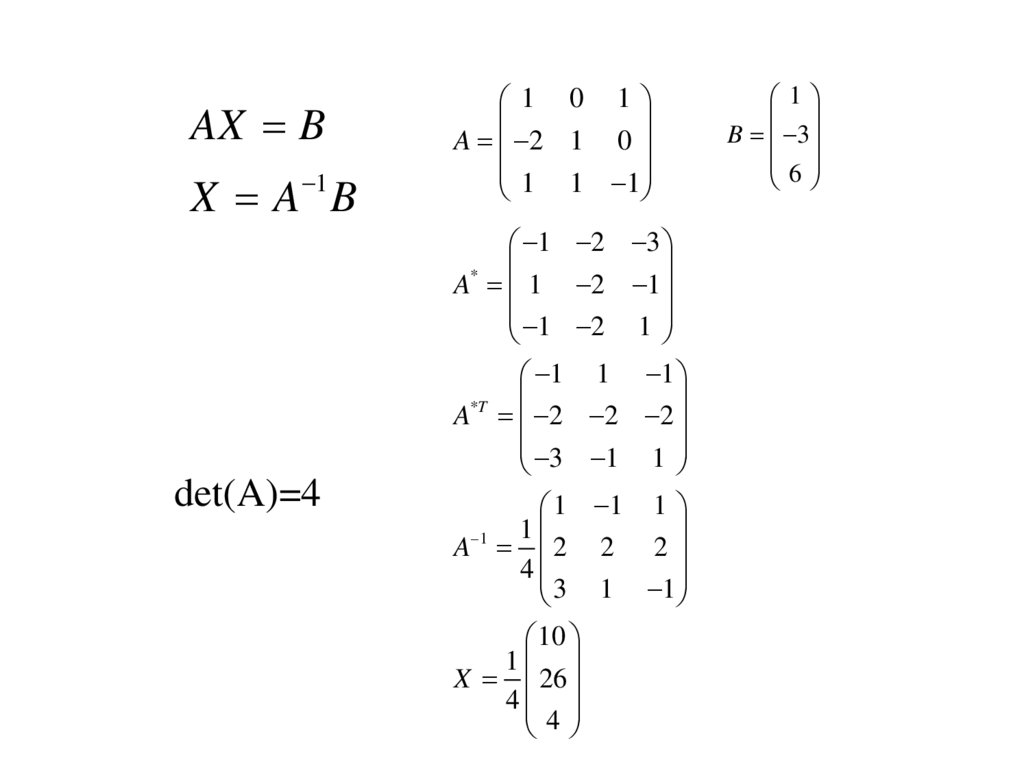



 mathematics
mathematics








