Similar presentations:
Понятие логарифма
1.
Определение• Логарифмом (обыкновенным)
положительного числа в по положительному
и отличному от 1 основанию а называют
показатель степени, в которую нужно
возвести число а, чтобы получить число в.
• Например: (логариф 8 по основанию 2 равен 3)
log
3
2
8
28
3
1
1
3
log
3
3
3
27
27
2.
3.
4.
5.
Свойства логарифмов1.aloga b b,
(
a
0
,a
1
,b
0
)
a
0
,a
1
,b
0
,c
0
)
2
.
log
b
log
c
log
(
b
c
),(
a
a
a
b
3
.
log
b
log
c
log
(),
a
a
a
c
(
a
0
,a
1
,b
0
,c
0
)
p
4
.log
b
p
log
,
a
ab
(
a
0
,a
1
,b
0
)
1
5
.log
log
,
pb
ab
a
p
(
a
0
,a
1
,b
0
)
1
6
.log
,
ab
log
ba
(
a
0
,a
1
,
b
0
,
b
1
)
6.
Вычислить:1.log216
1
6.log2
8
1
11.log
3
3
2.log
2 64
7.log
1 16
12
.log
381
2
3.log2 2
8.log
1 32
2
13
.log
1 27
3
4.log2 1
1
9.log
1
2 64
1
14.log
1
39
1
5.log2
2
1
10
.log
1
24
15.log1 1
3
7.
,log a b
logcb =
log a c
8.
Свойства логарифмовloga b
a
Например:
,a
1
,b
0
)
b, (a 0
3log3 5 5.
Вычислить:
log
0,57
1
2
2
0
,25
log
327
log
4
0
,25
9.
Свойства логарифмов0
,a
1
,b
0
,c
0
)
log
b
log
c
log
(
b
c
),(a
a
a
a
Например:
log
18
log
2
log
(
18
2
)
log
36
2
6
6
6
6
Вычислить:
1
log
log
550
5
2
1
1
(log
log
125
)
1
1
4 525 5
log
2
log
9
5
18
18
log
20
log
3
,2
3
2
2
10.
Свойства логарифмовb
a
0
,a
1
,b
0
,c
0
)
log
b
log
c
log
(),(
a
a
a
c
Например:
48
log
48
log
4
log
(
)
log
12
1
.
12
12 12
12
4
Вычислить:
1
.log
162
log
6
3
3
2
.log
108
log
3
6
6
3
.log
250
log
10
5
5
11.
Свойства логарифмов,a
1
,b
0
)
log
p
log
, (a 0
ab
ab
p
Например:
1
7
3
Вычислить:
1
1 1
log
3
log
3
1
.
3
7
7 7
1
log
3
log
3
32
4
log
100
log
10
3
log
2
5
5
5
1
log
2
log
14
7
7
28
12.
Свойства логарифмов1
log
log
, (a
0
,a
1
,b
0
)
pb
ab
a
p
Например:
log
4
log
4
2
log
4
2
2
4
1
2
2
2
2
Вычислить:
1.log3 27
2.log
1
8 2
3
.5 log
3
81
13.
Свойства логарифмов1
log
,(
a
0
,a
1
,b
0
,b
1
)
ab
log
ba
Например:
log
3
log
5
4
1
4
3
5
3
Вычислить:
log
log
325
581
log
6 log
7
49
36
log
log
8
5
26
36






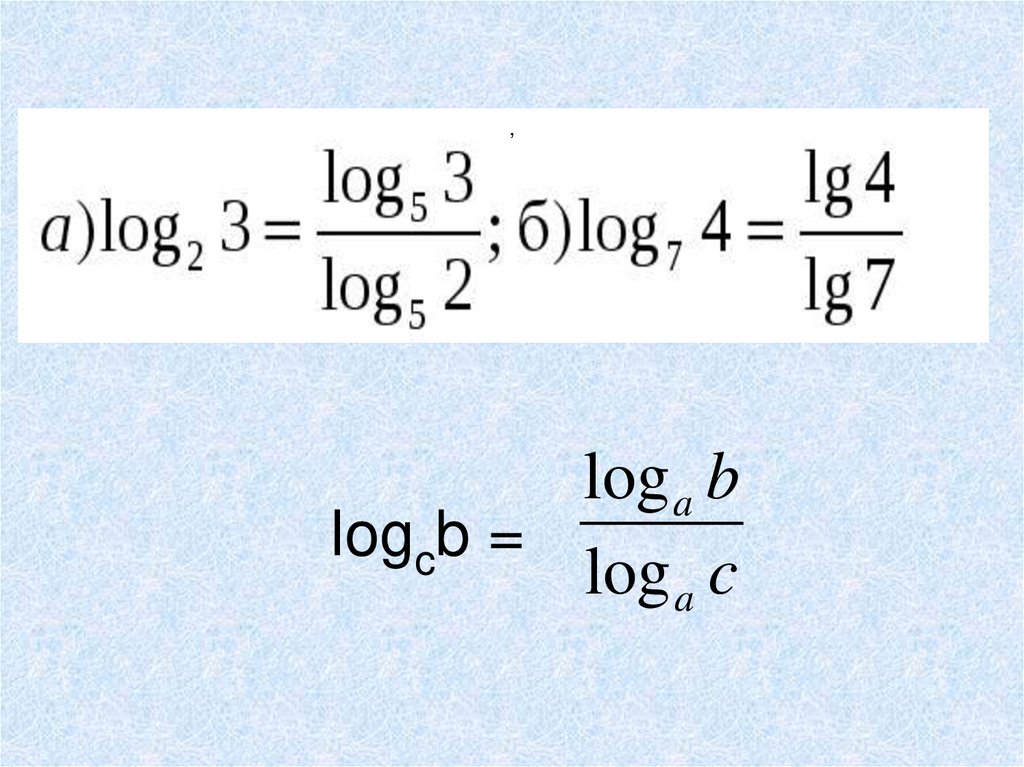







 mathematics
mathematics








