Similar presentations:
Критерии надежности невосстанавливаемых систем. (Лекция 2)
1. Лекция 2
Критерии надежности2. Критерии надежности невосстанавливаемых систем
Интервал времени от моментавключения до отказа – случайная
величина ξ.
Функция распределения
времени безотказной работы:
F(t) =P{ξ < t }
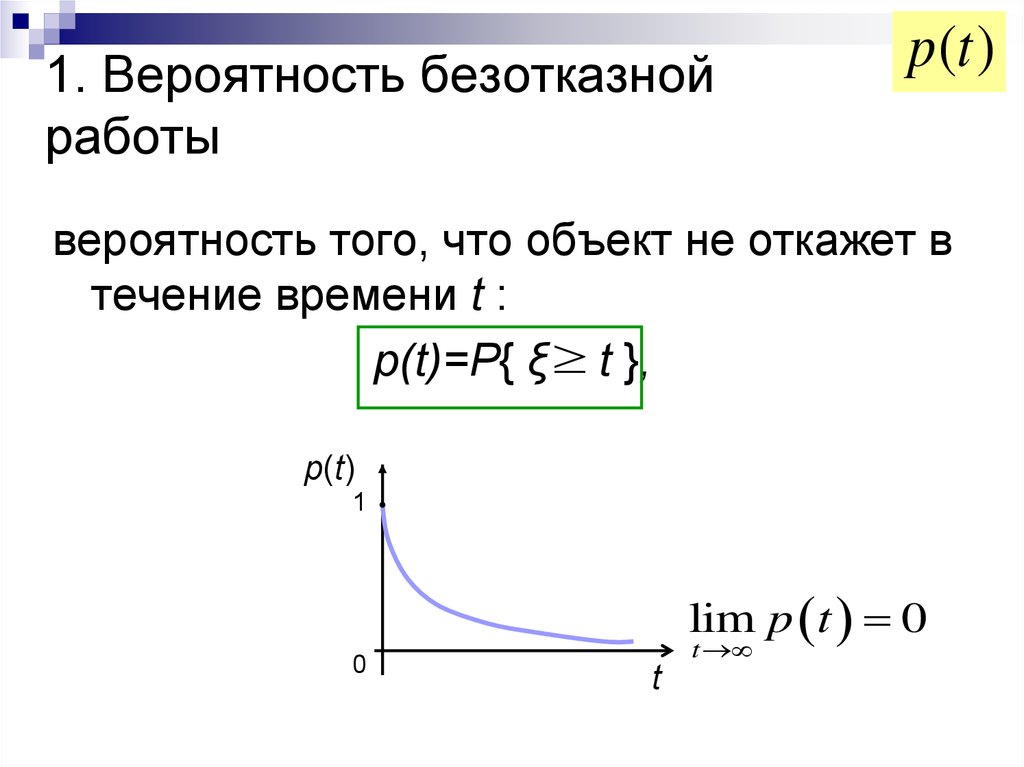
3. 1. Вероятность безотказной работы
p (t )вероятность того, что объект не откажет в
течение времени t :
р(t)=P{ ξ t },
p(t)
1
lim p t 0
0
t
t
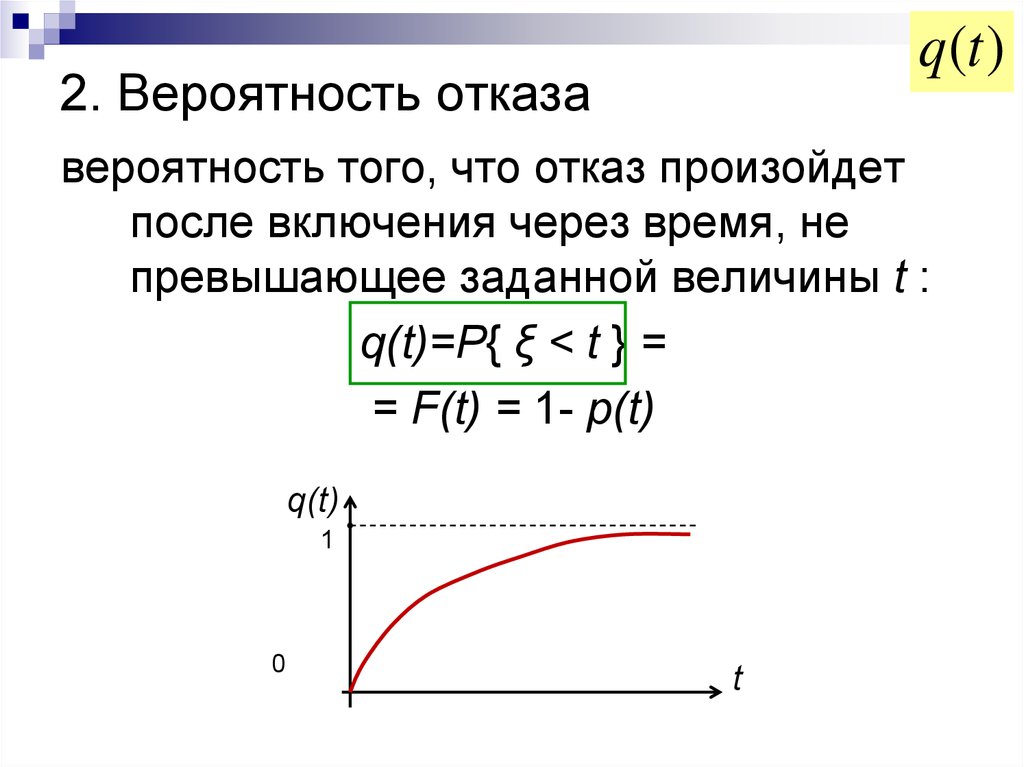
4. 2. Вероятность отказа
q(t )2. Вероятность отказа
вероятность того, что отказ произойдет
после включения через время, не
превышающее заданной величины t :
q(t)=P{ ξ < t } =
= F(t) = 1- р(t)
q(t)
1
0
t
5. 3. Плотность распределения времени безотказной работы
dF tf t
dt
dq t
dp t
f t
dt
dt
f(t)dt – характеризует безусловную
вероятность отказа за dt.
t
q(t )
0
f ( x)dx
t
0
t
p(t ) 1 f ( x)dx
f ( x)dx
f (t )
6. 4. Среднее время безотказной работы (математическое ожидание)
TT m1 tf (t )dt
0
Интегрируя по частям, получим
T t q' (t )dt t p' (t ) dt tp(t ) | ( p(t )) dt
0
0
0
0
полагая, что lim tp(t ) 0
t
T p(t )dt
0
7.
или так:dq (t )
T tf (t ) dt t
dt
dt
0
0
1
0
0
t dq p (t )dt
q(t)
S
1
p(t*)
dq
q(t*)
0
t
t*
8. Дисперсия времени безотказной работы:
2 m2 T 2 ,где m2 t f t dt 2ой начальный момент,
2
0
2 2 tp t dt T 2
0
9. 5. Вероятность безотказной работы на интервале
а) условная вероятность того, что время безотказнойработы будет больше t2, при условии, что в момент t1
объект был работоспособен:
p t 2 | t1 P{ t 2 | t1}
0
t1
t2
t
p t 2 1 F t 2
p t1 1 F t1
б) вероятность попадания времени отказа в интервал
(t1, t2):
p t1 , t 2 P{t1 t 2 }
p t1 p t 2
10. 6. Интенсивность отказов
tдифференциальная вероятность отказа в
момент t при условии, что после включения до t
устройство работало безотказно.
0
t
t+
t lim
0
q
11.
p tq 1 p 1
p t
p t p t
p t
p t p t
t lim
0
p t
p ' t
f t
, t
p t
p t
12. Выразим p(t):
p ' tt
p t
t
t dt ln p t
0
t
p t e
x dx
0
t2
Аналогично : p t1 , t2 e
t dt
t1
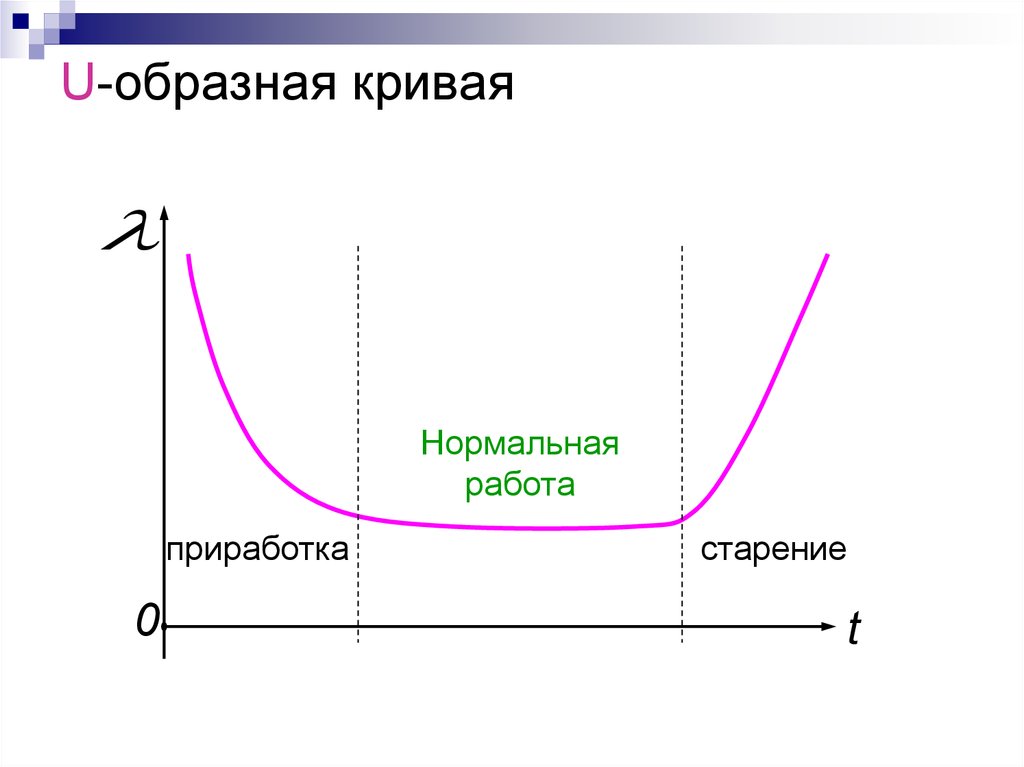
13. U-образная кривая
Нормальнаяработа
приработка
0
старение
t
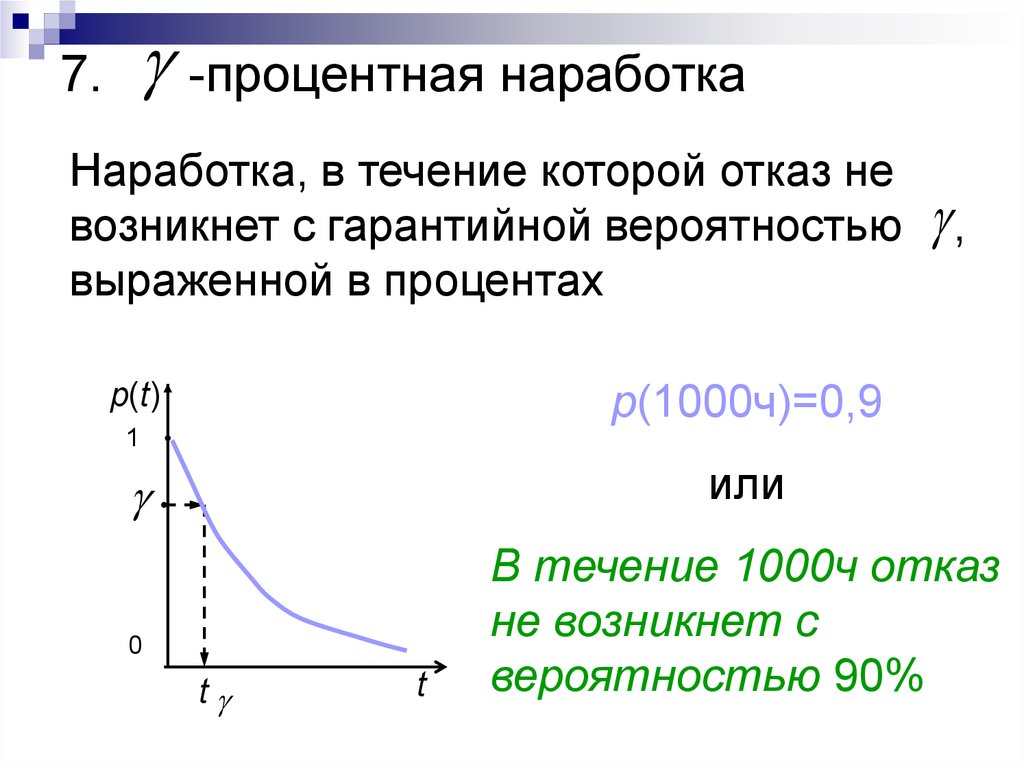
14. 7. -процентная наработка
Наработка, в течение которой отказ невозникнет с гарантийной вероятностью
выраженной в процентах
p(t)
,
p(1000ч)=0,9
1
или
0
t
t
В течение 1000ч отказ
не возникнет с
вероятностью 90%
15. Критерии надежности восстанавливаемых систем
S1S0
1
1 2
2
3
3 …
…
S1 – отказ (восстановление)
S0 – работа
Предположим, что все i независимые случайные
величины с одинаковым распределение Fв(t).
Восстановление – случайное событие,
интервал времени от момента отказа до
восстановления
16. 1. Вероятность восстановления за время t
рв(t) – вероятность того, что после отказаобъект будет восстановлен за время, не
превышающее заданную величину t :
рв(t) =P{ < t} = Fв(t)
qв(t) – вероятность невосстановления, т.е.
вероятность того, что ≥t :
qв(t) = 1- рв(t)
17. 2. Плотность вероятности момента восстановления:
dpB (t )f B (t )
dt
3. Среднее время восстановления:
0
0
Tв qв (t )dt 1 pв t dt
Дисперсия времени восстановления:
в 2 t 1 pв t dt Tв
2
0
2
18. 4. Интенсивность восстановления
f в tt
1 pв t
t
pв t 1 e
x dx
0
Замечание: в общем случае вероятностные
характеристики безотказности и
восстанавливаемости независимы
19. Вероятностные характеристики потока отказов
Было:интервал от включения до 1-го отказа;
интервал одного восстановления.
Интересна последовательность:
Работа отказ_восстановление работа … поток отказов
Предположим:
потоки отказов и восстановлений (каждый в
отдельности и совместно) - последовательности
независимых случайных событий;
на интервале восстановления отказы не возникают;
на малом интервале времени может появиться
только один отказ – ординарность.
20. Интервалы между отказами
работавосстановление
1 0
2
1
2 3 3
1 1 0
0
1
1 1 0
2
…
n
2 2 2
2
t
1 , , n CВ, моменты отказов
n
k k k 1 k k
n k
интервалы между отказами ,
k 1 n, 0 0
k 1
21. Функция распределения числа отказов Fn(t)
вероятность того, что момент n-го отказапредшествует t :
Fn t P n t P k t
k 1
n
Определение Fn(t) – задача о распределении
суммы конечного числа независимых СВ
решение: метод характеристических функций
результат: зависимость Fn(t) от характеристик
безотказности и восстанавливаемости
22. Число отказов
t - дискретная СВ, число отказов на (0,t)Fn(t) – вероятность того, что момент n отказа
предшествует t = вероятности того, что на
(0,t) произошло по крайней мере n отказов
Fn t P t n
Вероятность появления на (0,t) точно n
отказов:
P t n P t n P t n 1
Fn t Fn 1 t
23. Среднее число отказов на (0,t)
H t m1 t n P t nn 0
n 0
n 0
n Fn t n Fn 1 t см. *
Fn t
n 1
0 1F1 t 2F2 t 3F3 t nFn t 1F2 t 2F3 t n 1 Fn t *
24. Параметр потока отказов
производная (скорость изменения) среднегочисла отказов в момент t
dH t
t
dt
Асимптотическое значение:
lim t
t
1
T Tв
Свойства (при мгновенном восстановлении: Tв=0):
для экспоненциального распределения времени
безотказной работы с параметром : t ;
связь с плотностью распределения времени до
отказа (интегральное уравнение Вольтерра):
t
t f t f t d
0
25. Функция готовности
Вероятность того, что восстанавливаемаясистема исправна в момент t:
t
G t p t p t d
0
Коэффициент готовности:
K г lim G t
t
Коэффициент простоя:
T
Kг
T Tв
,
Kп 1 Kг
Tв
Kп
T Tв
.





















 mathematics
mathematics physics
physics








