Магнитный момент электронной оболочки атома

1. Кислицын А.А. Физика атома, атомного ядра и элементарных частиц

23 (2). Магнитный момент
электронной оболочки атома.

2.

Выше (в презентации 15) были рассмотрены орбитальный μl и собственный μs моменты электрона.
Сумма этих моментов определяет полный магнитный момент электронной оболочки атома.
Найдем этот момент с помощью векторной диаграммы. Изображая на векторной диаграмме
магнитные моменты необходимо учесть, что гиромагнитное отношение для собственных моментов электрона вдвое больше отношения для
орбитальных моментов Вследствие этого направление вектора полного магнитного момента
атома μ не совпадает с направлением полного
механического момента J.

3.

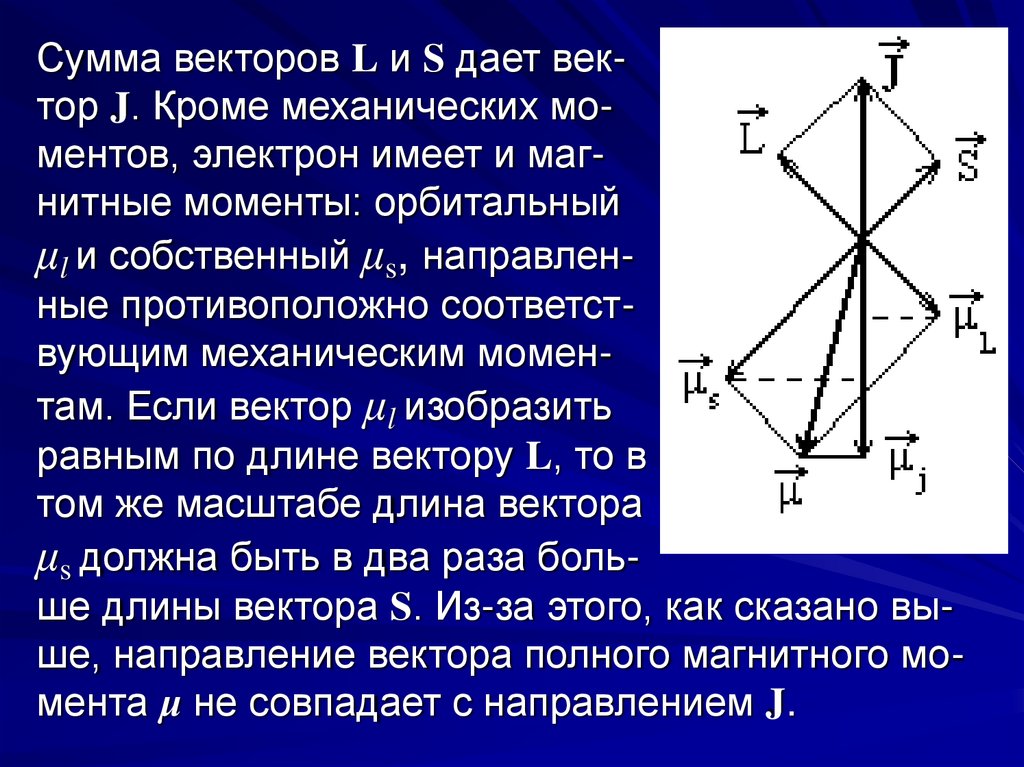
Сумма векторов L и S дает вектор J. Кроме механических моментов, электрон имеет и магнитные моменты: орбитальный
μl и собственный μs, направленные противоположно соответствующим механическим моментам. Если вектор μl изобразить
равным по длине вектору L, то в
том же масштабе длина вектора
μs должна быть в два раза больше длины вектора S. Из-за этого, как сказано выше, направление вектора полного магнитного момента μ не совпадает с направлением J.

4.

На полуклассическом языке можно сказать,
что векторы L и S, а вместе с ними векторы μl и μs, прецессируют (вращаются) вокруг вектора J. Поэтому средние значения
проекций, перпендикулярных к J, равны
нулю (точнее говоря, эти проекции неопределенны), а определенное значение
имеет только одна проекция вектора μ проекция μj на направление вектора J. Эта
величина называется эффективным
полным магнитным моментом электронной оболочки атома.

5.

Найдем эту величину, для чего
сложим проекции векторов μl и μs
на направление J:
j l cos L, J s cos S, J
Для определения косинусов воспользуемся теоремой косинусов
из элементарной геометрии
L J S 2 J S cos S, J
2
2
2
cos S, J
J S L
2
2
2J S
2
2
j( j 1) s(s 1) l (l 1)
2
j ( j 1)
s(s 1)

6.

Аналогично
S J L 2 L J cos L, J
2
2
2
cos L, J
Поэтому
j 0
2 0
J L S
2
2
2J L
2
h 2 j ( j 1) l (l 1) s ( s 1)
2
j ( j 1)
l (l 1)
j ( j 1) l (l 1) s ( s 1)
l (l 1)
2 j ( j 1) l (l 1)
j ( j 1) s ( s 1) l (l 1)
s ( s 1)
2 j ( j 1) s ( s 1)
3 j ( j 1) s ( s 1) l (l 1)
0
2 j ( j 1)
.

7.

Умножим числитель и знаменатель последней дроби на
j ( j 1) :
j 0
j ( j 1) s( s 1) l (l 1)
j ( j 1) 1
2 j ( j 1)
Обозначим выражение, стоящее в фигурных скобках:
j ( j 1) s( s 1) l (l 1) (23.1)
g 1
2 j ( j 1)
Эта величина называется множителем (фактором)
Ланде (Lande A.) и определяет гиромагнитное отношение для эффективного полного момента электронной оболочки атома.

8.

Итак, эффективный магнитный момент
электронной оболочки атома равен:
j 0 g j ( j 1)
(23.2)
а гиромагнитное отношение для μj :
j
J
0 g j ( j 1)
j ( j 1)
0
e
g
g
2m0
(23.3)

9.

Если поместить атом в магнитное поле то он будет
вести себя как диполь с моментом μj, причем ориентация этого момента будет определяться проекциями вектора J на направление магнитного поля:
jB j cos J, B
Чтобы найти cos J, B воспользуемся формулами
(19.5) и (19.6). Согласно формуле (19.5), проекция
момента J на направление B равна
J m ,
B
j
где магнитное внутреннее квантовое число принимает значения:
m j j , j 1, j 2, ..., j

10.

С другой стороны, ту же проекцию можно выразить с помощью косинуса угла между векторами J и B:
JB
отсюда
j ( j 1) cos J, B
cos J, B
mj
j ( j 1)
Таким образом, проекция эффективного магнитного момента атома на направление внешнего
магнитного поля равна:
jB j cos J, B j
0 g j ( j 1)
mj
j ( j 1)
mj
j ( j 1)
0 gm j
(23.4)

11.

Отсюда можно найти потенциальную энергию взаимодействия магнитного момента
атома с внешним магнитным полем:
E j B jB B 0 gBm j (23.5)
Эта энергия зависит от величины фактора
Ланде g, определяемого формулой (23.1),
и принимает ряд дискретных значений,
определяемых магнитным внутренним
квантовым числом mj.

12.

Полученный результат легко обобщить на
магнитный момент многоэлектронного
атома. Как было отмечено выше, для
большинства атомов имеет место нормальная (LS) связь между электронами,
поэтому магнитный момент электронной
оболочки многоэлектронного атома равен
сумме орбитальных и спиновых моментов
электронов:
l l l ... s s s ...
1
2
3
1
2
3

13.

При помощи векторной диаграммы аналогично тому, как это было сделано для одного электрона,
можно показать, что эффективный магнитный
момент электронной оболочки многоэлектронного атома равен
J 0 g J ( J 1)
где множитель Ланде
J ( J 1) S ( S 1) L( L 1)
g 1
2 J ( J 1)
а внутреннее квантовое число J принимает значения
J L S , L S 1, ..., L S

14.

Во внешнем магнитном поле B вектор μJ может ориентироваться относительно этого поля только так, что его проекция на направление B равна
JB J cos J, B
0 g J ( J 1)
MJ
J ( J 1)
(23.6)
0 gM J
где MJ (аналог числа mj) принимает значения:
M J J , J 1, ..., J
(всего 2J+1 значений)

15.

Следствием принципа Паули является то, что у
любой полностью заполненной (замкнутой) оболочки суммарные орбитальный, спиновый и полный моменты импульса равны нулю:
L 0, S 0, J 0
Действительно, т.к. ms = ±1/2, m = 0, ±1, ±2, …, ±l, то
для замкнутой оболочки ∑ml = 0 и ∑ms = 0, т.к.
суммирование ведется по всем электронам.
Отсюда следует, что и магнитный момент замкнутой оболочки равен нулю. Поэтому и механический, и магнитный моменты электронной оболочки атома определяются лишь электронами, находящимися в незаполненных оболочках (валентными электронами).