Similar presentations:
Приложение: водородоподобный атом; вывод формул
1. Кислицын А.А. Физика атома, атомного ядра и элементарных частиц
14 (2). Приложение: водородоподобныйатом; вывод формул.
2.
Уравнение Шредингера для водородоподобного атома имеет вид:2m
Ze2
(14.1)
2 E
0
4 0 r
где оператор Лапласа:
2 2
1
1
2
2
2
sin
2 2
r
r r r sin
r sin 2
(14.2)
Решение этого уравнения впервые получил Шредингер в 1926 году. Решение можно найти теми же методами, которыми были решены предыдущие задачи, но в данном случае процедура решения оказывается довольно сложной, а преобразования
громоздкими. Применение операторов позволяет
сделать выкладки более компактными.
3.
Запишем оператор Лапласа в виде1 2 1 ˆ
2 r
2
r r
r r
(14.3)
где ̂ - оператор Лежандра (13.20). Решение уравнения Шредингера ищем в виде произведения:
(14.4)
r , , R r Y ,
где R(r) и Y(θ,φ) - неизвестные пока функции, зависящие только от r и от θ,φ соответственно. Обозначим для краткости:
2m
Ze2 m
E ,
2
2
(14.5)
Подставляя в уравнение (14.1) и разделяя переменные, получаем:
1 d 2 dR 2
2 1 ˆ
r
r
Y
(14.6)
R dr r
r Y
4.
Левая часть уравнения (14.6) зависит только от r,правая часть только от θ, φ, поэтому для того, чтобы равенство (14.6) удовлетворялось для любых r,
θ, φ, необходимо, чтобы левая и правая части равнялись некоторой константе λ:
1 d 2 dR 2
2
(14.7)
r
r
R dr
и
1 ˆ
Y
Y
r
или
r
ˆ Y Y
(14.8)
В уравнение (14.7) входит потенциальная энергия
кулоновского взаимодействия электрона с ядром
(член 2α/r), поэтому вид функций R(r) и собственные значения энергии определяются этим конкретным видом взаимодействия.
5.
Уравнение (14.8) более универсально: оно одинаково для всех сферически - симметричных полей, поэтому займемся сначала этим уравнением. Запишем его в раскрытом виде:1
Y
1 Y
Y 0
sin
2
2
sin
sin
2
(14.9)
Это уравнение допускает дальнейшее разделение
переменных. Будем искать функции Y(θ,φ) в виде:
Y , P ( )
(14.10)
Подставляем (14.10) в (14.9), и разделяем переменные:
sin
P
1
2
sin
sin
P
2 (14.11)
2
6.
Левая часть уравнения (14.11) зависит только от θ,правая часть только от φ, поэтому для того, чтобы
равенство (14.11) удовлетворялось для любых θ, φ,
необходимо, чтобы левая и правая части равнялись некоторой константе, которую обозначим в
2
виде m2:
d
2
m
0
(14.12)
2
d
2
1 d
dP
m
sin
2
sin d
d
sin
P 0 (14.13)
Сначала займемся уравнением (14.12). Его решение
хорошо известно:
( ) Aeim Be im
где A и B - некоторые константы.
(14.14)
7.
Очевидно, что решение (14.14) удовлетворяет условию ограниченности. Но т.к. φ - циклическая переменная, а область ее изменения 0 ≤ φ ≤ 2π, то, независимо от значений констант А и В, для выполнения условия однозначности решения необходимо, чтобыe
im
e
im ( 2 )
e
im
e
i 2 m
Отсюда видно, что решение будет однозначным, если
i 2 m
e
1
а это возможно только если m - целое число, включая отрицательные значения и нуль:
m = 0, ±1, ±2, …
(15)
8.
Теперь рассмотрим уравнение (14.13). Введем вместо θ новую переменную ξ:ξ = cosθ,
-1 ≤ ξ ≤ +1,
dξ = - sinθdθ, (14.16)
и будем рассматривать P как функцию ξ. Тогда уравнение (14.13) принимает вид:
2
dP
dP
m
2
1 d 2 d 1 2 P 0
(14.17)
Решение уравнения (14.17) ищется в виде степенного ряда, подобно тому, как это было сделано при
решении уравнения (12.6). Функция P(cosθ) должна
быть непрерывной и конечной при всех углах θ.
Чтобы удовлетворить этому условию, параметр λ
должен быть равен:
λ = l(l + 1),
(14.18)
где l - неотрицательное целое число.
9.
Функции P(ξ) называются "присоединенными полиномами Лежандра", их общий вид был найден еще в18-м веке французским математиком А.М.Лежандром (A.M.Legendre):
1
Pl l 1
2 l!
m
2 m/2
d
l m
l m
2
1
l
(14.19)
Т.к. уравнение (14.17) содержит 2 целочисленных
параметра m и λ = l(l + 1), то формула для полинома P также содержит 2 параметра, которые называются "квантовыми числами" m и l. Например:
P00 1,
P10 cos ,
P11 sin
и т.д. То, что указанные функции действительно являются решениями уравнения (14.17), проще всего
проверить прямой подстановкой.
10.
Определив константу λ = l(l+1), подставим ее в уравнение (14.7) 1 d dR2
2
2
r
r
l l 1 (14.20)
R dr r
r
Решение этого уравнения также давно известно. Оно
ищется в виде степенного ряда аналогично тому,
как это было сделано при решении предыдущих
задач. Функция R(r) называется радиальной волновой функцией (т.к. зависит только от одной координаты r), и выражается через полиномы, которые
называются полиномами Лагерра. Кроме квантового числа l, в эти полиномы входит еще одно квантовое число n, которое определяет энергию взаимодействия электрона с ядром.
11.
Наиболее простые из полиномов Лагерра имеют вид:(14.21)
r
r / 2
r / 2
R
e
,
R
2
r
e
,
R
re
(собственные
Итак, волновые
20
-функции
функции
10
21
уравнения (14.1)) содержат три целочисленных параметра (квантовые числа n, l и m):
(14.22)
r
,
,
R
r
P
e
nlm
nl
l
Например:
m
211 Are
r / 2
sin e
im
i
Общая теория этих функций описана, например, в
учебнике: В.И.Смирнов. Курс высшей математики,
том III, часть 2.
12.
Подведем итоги. Энергия электрона определяетсяформулой, в точности совпадающей с результатом, полученным в рамках теории Бора:
2
1 Z me e
En = - 2
2 2
n 8h ε0
4
(14.23)
где n = 1, 2, 3, ... - "главное квантовое число". Часто
применяются следующие условные обозначения
и термины: K-слой, L-слой и т.д.:
n
1
2
3
4
5
6
...
Условное
обозначение
K
L
M
N
O
P
...
13. Схематическое изо- бражение уровней энергии и переходов между ними в атоме водорода
Схематическое изображение уровнейэнергии и переходов
между ними в атоме
водорода
14.
Уровни энергииатома водорода.
Толщина линии
соответствует
вероятности
перехода.
15.
Момент импульса электрона в атоме определяется орбитальным квантовым числом l:L=
l (l +1)
(14.24)
где орбитальное квантовое число l может принимать значения l = 0, 1, 2, ..., (n-1). Часто применяются следующие условные обозначения и термины: s-оболочка, p-оболочка и т.д.:
l
0
1
2
3
4
5
...
Условное
обозначение
s
p
d
f
g
h
...
16.
Проекция момента импульса на выделенное направление (например, на направление внешнего магнитного поля) определяется магнитнымквантовым числом m:
(14.25)
LZ = m
Магнитное квантовое число может принимать значения:
m = 0, ±1, ±2, …, ± l,
или:
m = -l, -l+1, -l+2,..., 0, 1, 2, ..., l
всего (2l + 1) значений.
17.
Для наглядности пространственное квантование вектора момента импульса часто изображают графически на векторных диаграммах:l=1
l=2
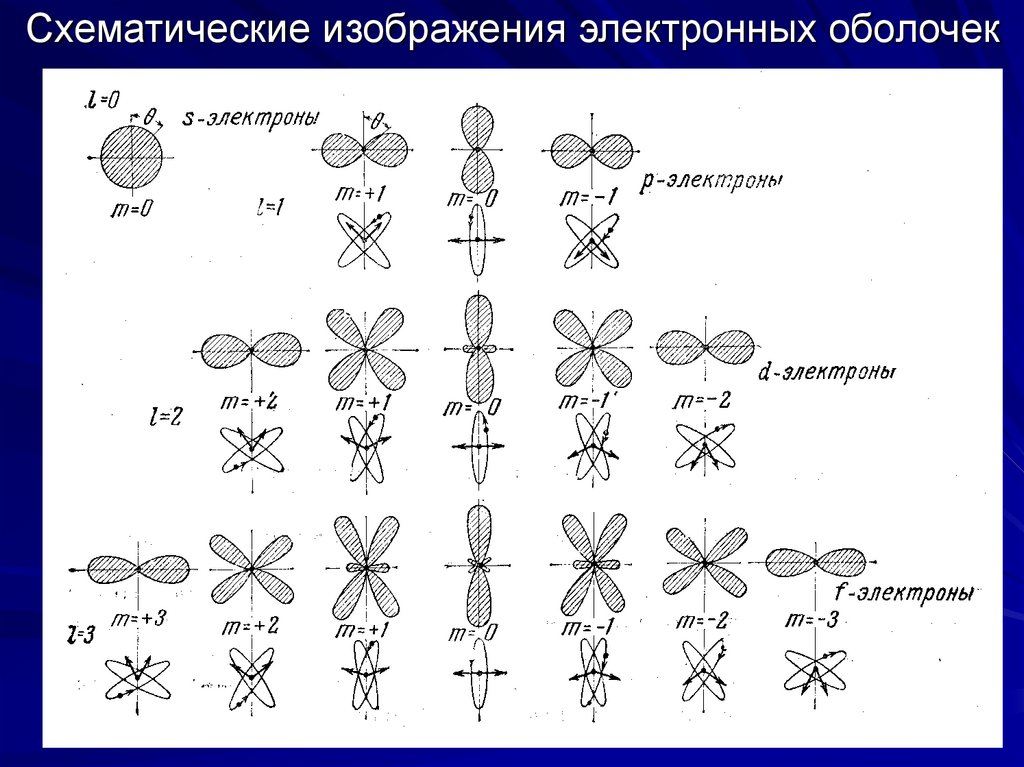
18. Графические изображения электронных s-, p- и d-оболочек
Графическиеизображения
электронных
s-, p- и dоболочек




















 physics
physics








