Фазовая и групповая скорость волн де-Бройля. Волновой пакет

1. Кислицын А.А. Физика атома, атомного ядра и элементарных частиц

6. (1). Фазовая и групповая скорость
волн де-Бройля. Волновой пакет.

2.

ФАЗОВАЯ СКОРОСТЬ
Плоская монохроматическая волна с амплитудой А,
частотой и волновым вектором k может быть
представлена в комплексной форме в виде:
r, t Ae
i t k r
Ae
i
Et p r
(6.1)
Фазовой скоростью волны называется скорость, с
которой движутся точки волны с постоянной фазой. Если ось x направлена по вектору p, то условие постоянства фазы
Et - px = const.
(6.2)
Чтобы вычислить фазовую скорость, надо продифференцировать это уравнение по времени.

3.

dx
Продифференцируем (6.2) по времени: E p
0
dt
dx E
dx
, где
vф - фазовая скорость.
откуда
dt p
dt
E
По формулам (5.2) и (5.3) находим:
p
k k
2
2
E mc
c
С другой стороны:
p mv
v
где v - скорость частицы.
Итак, фазовая скорость:
2
c
vф
k
v
(6.3)

4. Суперпозиция волн

Рассмотренная выше плоская монохроматическая
волна представляет собой строго периодический
процесс, бесконечно протяженный в пространстве
и во времени. Это абстракция: ни в природе, ни в
технике такие волны не существуют. Любой реальный процесс имеет начало и конец, он ограничен
как во времени, так и в пространстве и не является строго гармоническим. Его можно рассматривать как результат суперпозиции (наложения)
некоторого количества монохроматических волн,
которые вследствие интерференции в одних частях пространства усиливают друг друга, а в других
- гасят друг друга.

5. Образование волновой группы

Рассмотрим простейший случай: суперпозицию двух
волн
u1 a cos 1t k1 x , u2 a cos 2t k2 x
распространяющихся вдоль оси x. Будем считать,
что частоты 1 и 2, а также абсолютные значения
волнового вектора k1 и k2 очень мало отличаются
друг от друга. Складывая u1 и u2, находим:
u u1 u2 a cos 1t k1 x a cos 2t k2 x
k1 k2
1 2
2a cos
t
2
2
Обозначим:
1 2
2
k1 k2
1 2
x cos
t
2
2
x
k1 k2
1 2 k1 k2 k
,
k,
,
2
2
2
2
2

6.

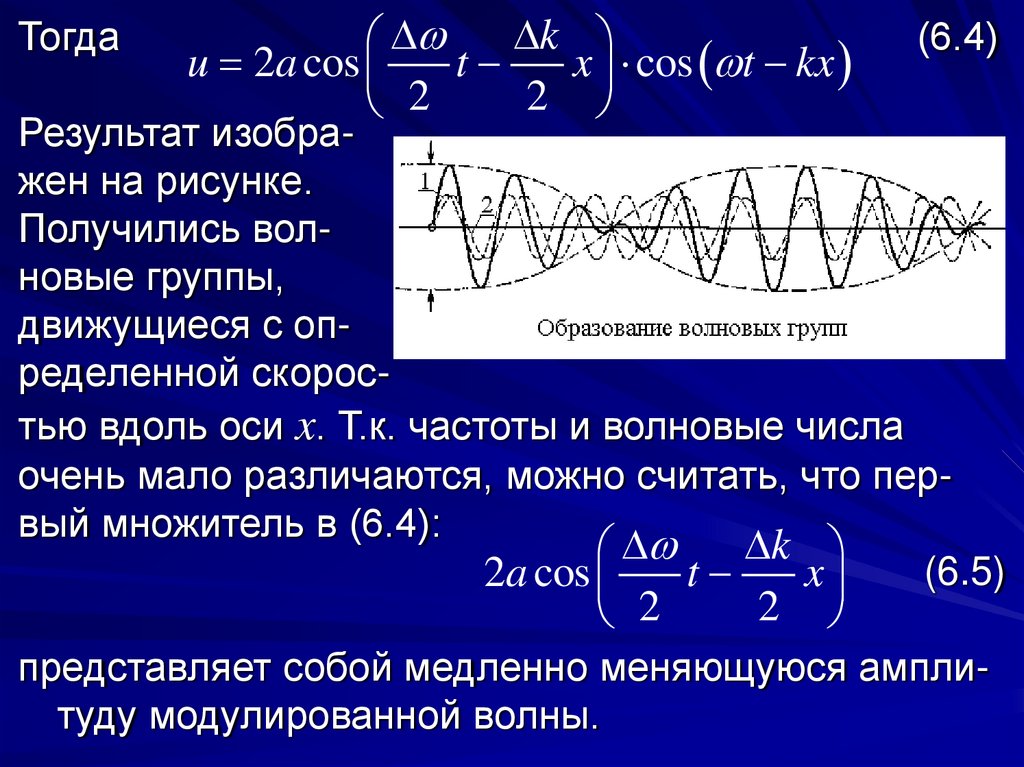
Тогда
k
u 2a cos
t
2
2
x cos t kx
(6.4)
Результат изображен на рисунке.
Получились волновые группы,
движущиеся с определенной скоростью вдоль оси x. Т.к. частоты и волновые числа
очень мало различаются, можно считать, что первый множитель в (6.4):
k
(6.5)
2a cos
t
x
2
2
представляет собой медленно меняющуюся амплитуду модулированной волны.

7. ГРУППОВАЯ СКОРОСТЬ

Скорость перемещения волновой группы - это скорость перемещения определенной амплитуды.
Для ее определения запишем условие постоянства амплитуды:
k
t
x const
(6.6)
2
2
Дифференцируя (6.6) по t, получаем скорость перемещения волновой группы:
dx
vгр
В пределе
k 0
повой скорости:
dt
k
получаем формулу для груп-
d
vгр
dk
(6.7)

8. ГРУППОВАЯ СКОРОСТЬ ВОЛН ДЕ-БРОЙЛЯ

Для волн де-Бройля:
d d dE
vгр
dk d k dp
cp
2
d c p 2 m02 c 2
dp
2
(6.8)
c p c mv
v
2
2
2 2
E
mc
p m0 c
Таким образом, "обычная", т.е. измеряемая в
эксперименте скорость частицы v равна
групповой скорости волн де-Бройля vгр

9.

СООТНОШЕНИЕ МЕЖДУ ФАЗОВОЙ И ГРУППОВОЙ
СКОРОСТЬЮ ВОЛН ДЕ-БРОЙЛЯ
Вернемся к формуле (6.3) и запишем ее в виде
c2
c
vф c
v
v
или
vф v c2
(6.9)
Из этой формулы следует, что фазовая скорость
волн де-Бройля всегда больше скорости света (т.к.
скорость частицы v всегда меньше скорости света). Это, однако, не противоречит теории относительности, т.к. фазовая скорость не характеризует
ни скорость перемещения массы, ни скорость перемещения энергии.

10. ВОЛНОВОЙ ПАКЕТ

Путем наложения (суперпозиции) плоских волн с
непрерывно меняющимися волновыми числами
можно осуществить такой
волновой процесс, при котором амплитуда волны будет заметно отличаться от нуля только в небольшой части
пространства, а в остальном пространстве будет почти равна нулю. Такой волновой процесс называется волновым пакетом.

11. ВОЛНОВОЙ ПАКЕТ

Вследствие непрерывного изменения волнового числа k сложение волн представляется интегралом
u
k0 k
a cos t kx dk
(6.10)
k0 k
где амплитуду a складываемых волн будем считать
постоянной во всем интервале от -Δk до +Δk.
Какова бы ни была зависимость частоты ω от волно-вого
числа k, ее можно представить в виде ряда
2
d
1
d
2
k k0 k k0
k k0 2 ...
dk k k0 2
dk k k
0
(6.11)

12. ВОЛНОВОЙ ПАКЕТ

Для малого интервала Δk в формуле (6.11) мо-жно
ограничиться первыми двумя членами
разложения. Подставляя в (6.10), получаем
k0 k
d
u a cos 0t k k0
t kx dk
dk 0
k0 k
где для краткости обозначено:
d d
0 k0 ,
dk
dk
0
k k0
(6.12)

13. ВОЛНОВОЙ ПАКЕТ

Интеграл (6.12) легко вычисляется с помощью за-мены
переменной. Обозначим
тогда
d
0t k k0
t kx z
dk 0
dz
dk
d
t x
dk 0
и интеграл (6.10) принимает вид:
k0 k
a
u
cos z dz
d
k0 k
t
x
dk 0

14.

Подставляя пределы и умножая числитель и знаменатель на Δk, получаем:
d
sin k
t x
dk 0
u 2a k
cos 0t k0 x
d
k
t x
dk 0
(6.13)
Этот результат можно интерпретировать так же, как
формулу (6.4): cos 0t k0 x представляет собой
рассматриваемый волновой процесс, а стоящий
перед ним множитель - переменную (модулированную) амплитуду:
d
sin k
t x
dk 0
A 2a k
d
k
t x
dk 0
(6.14)

15. Групповая скорость волнового пакета

d
k
t x
dk 0
Тогда формулу (6.14) можно записать в виде:
Обозначим:
A 2a k
(6.15)
sin
(6.16)
Таким образом, характер изменения амплитуды определяется множителем sin / , который при 0
равен 1 (точнее, имеет предел, равный 1 при 0 ).
При увеличении он убывает, и при , 2 ,...
обращается в нуль. В промежутках между этими
значениями он имеет второстепенные максимумы,
но с точностью 5% можно считать, что весь ход функции sin / сосредоточен на интервале , а за
пределами этого интервала он равен нулю.

16. Групповая скорость волнового пакета

Итак, множитель sin / при 0 имеет максимум,
равный 1. Скорость перемещения этого максимума можно считать скоростью перемещения всего
волнового пакета. Для ее определения запишем
условие 0 :
d
x
t 0
dk 0
Дифференцируя по t, находим:
dx d
vгр
dt dk 0
(6.17)
Сравнивая с формулой (6.7), видим, что скорость
перемещения волнового пакета равна групповой
скорости волн де-Бройля.

17. Волновой пакет

Итак, в результате суперпозиции
волн получился волновой пакет с
амплитудой
d
sin k
t x
dk 0
A 2a k
d
k
t
x
dk
0
примерный вид которой изображен на рисунке. Волновой пакет движется со скоростью, равной групповой скорости волн де-Бройля, которая, в свою очередь, равна скорости частицы. Ширина пакета Δx обратно пропорциональна интервалу Δk волновых чисел волн, образующих пакет:
1
(7.8)
x
k

18. Неустойчивость волнового пакета

Фазовая скорость
h
E
v
k
hk
p
p c m c
2
2
2
0
p
4
m0 c
c 1
p
2
зависит от импульса, и, значит, от волнового числа k
= p/h. Поэтому каждая из монохроматических
волн, входящих в пакет, распространяется со своей фазовой скоростью, и пакет "расплывается" за
m0
время
2
t
k
x
Для электрона это примерно 10-26 секунды, т.е. практически мгновенно.