Similar presentations:
1 лекция. Переходные процессы, законы коммутации. Классический метод расчета
1. 1 лекция
Переходные процессы,законы коммутации,
Классический метод расчета
2. Переходные процессы и законы коммутации
23.
Переходные процессывозникают при включении
или отключении источников,
элементов цепи, при коротких
замыканиях и обрывах проводов,
а также при различных импульсных
воздействиях на цепь, например,
при грозовых разрядах
3
4.
Переходный процесс илипереходный режим цепи – это
изменение во времени
напряжений и токов от одних
установившихся значений
к другим установившимся
значениям
4
5.
Установившиеся значениянапряжений и токов
характеризуют установившийся
режим цепи и могут оставаться
неизменными бесконечно долго,
причем эти значения
задаются источниками
электрической энергии
5
6.
При анализе и расчетепереходных процессов будем
считать, что
•переходные процессы возникают
при включении или отключении
элементов цепи посредством
ключей, причем эта коммутация
происходит мгновенно быстро
в момент времени t=0
6
7. Ключ замыкается:
78. Ключ замыкается:
89. Ключ замыкается:
910. Ключ размыкается:
1011. Ключ размыкается:
1112. Ключ размыкается:
1213. Ключ размыкается:
1314.
• при времени t=переходный
процесс теоретически заканчивается
и наступает новый установившийся
режим
•время t<0 характеризует режим
цепи до коммутации
• момент времени t=0- соответствует
последнему моменту перед
коммутацией
14
15.
• момент времени t=0+ соответствуетпервому моменту времени после
коммутации
• скачок – это мгновенное изменение
напряжения или тока при t=0+
15
16.
f(t)скачок
f (0 )
f (0 )
t
0
Установившийся
режим до
коммутации
tп
Переходный режим
Установившийся
режим после
коммутации
16
17. Законы коммутации
1718.
1. Первый закон коммутацииL
iL
+
uL
i L (0 ) i L (0 )
18
19.
Ток виндуктивности не
может измениться
скачком
19
20.
Это объясняется тем, что энергиямагнитного поля индуктивного
элемента WL=LiL2/2 , Дж
не может измениться мгновенно,
для чего потребовалась бы
бесконечно большая мощность
PL=dWL/dt=
, Вт
и бесконечно большое напряжение
uL=d(LiL)/dt= , В
а это не реально
20
21.
d iLuL L
dt
- напряжение может
измениться скачком
21
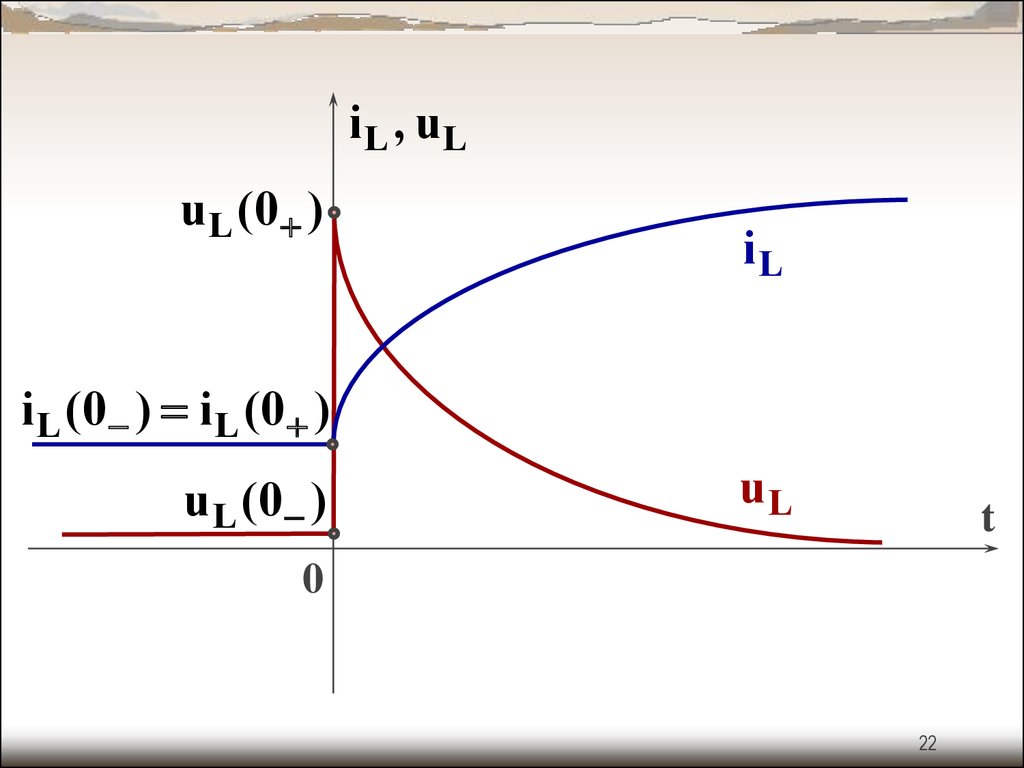
22.
i L , uLu L (0 )
iL
i L (0 ) i L (0 )
u L (0 )
uL
t
0
22
23.
2. Второй закон коммутацииС
iС
+
uС
uC ( 0 ) uC ( 0 )
23
24.
Напряжение наемкости не может
измениться скачком
24
25.
Это объясняется тем, что энергияэлектрического поля емкостного
элемента WC=CuC2/2 , Дж
не может измениться мгновенно,
для чего потребовалась бы
бесконечно большая мощность
PC=dWC/dt=
, Вт
и бесконечно большой ток
iC=d(CuC)/dt= , А
а это не реально
25
26.
d uCiС C
dt
- ток может
измениться скачком
26
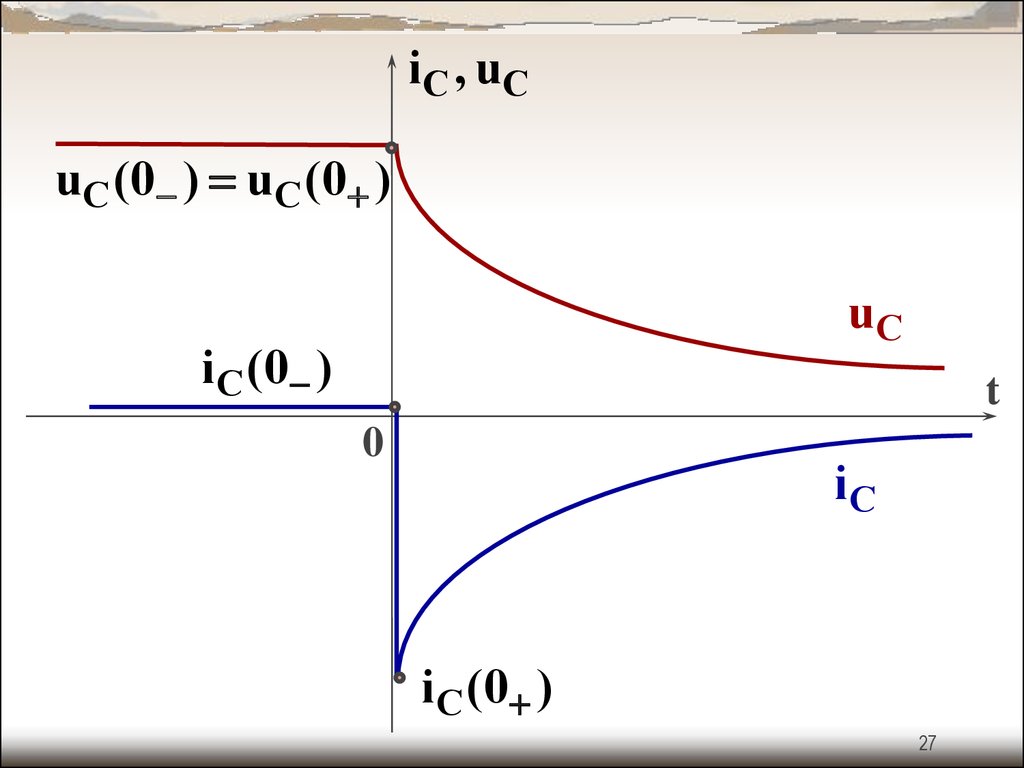
27.
i С , uСuC ( 0 ) uC ( 0 )
uС
i C ( 0 )
t
0
iС
i С ( 0 )
27
28.
Переходныйпроцесс обусловлен
наличием в цепи L
иC
28
29. К л а с с и ч е с к и й метод расчета переходных процессов
Классическийметод расчета
переходных
процессов
29
30.
Используется для линейныхцепей, которые
характеризуются линейными
дифференциальными
уравнениями, составляемыми
при помощи законов Кирхгофа
для цепи после коммутации
30
31.
nn 1
d f (t )
d f (t )
аn
а
...
n
1
n
n 1
dt
dt
df (t )
а1
а 0 f ( t ) F( t )
dt
- уравнение 1
31
32.
- это линейное неоднородноедифференциальное уравнение
n- порядка для тока или
напряжения f(t) переходного
процесса при t>0
(схема после коммутации)
32
33.
Где:an , an 1 , ... , a1 , a0
постоянные коэффициенты,
определяемые параметрами
(R, L, C) и структурой цепи
после коммутации
33
34.
Где:F(t )
функция, определяемая
(независимыми)
источниками цепи после
коммутации
34
35.
Решение уравнения 1:f (t ) fпр (t ) fсв (t )
2
35
36.
Где:fпр (t )
принужденная составляющая
– это частное решение
уравнения 1, зависящее от F(t)
36
37.
Где:fсв (t )
свободная составляющая
– это общее решение
однородного уравнения 1
при F(t) = 0
37
38.
При постоянных игармонических источниках
fпр (t )
это установившееся
значение после коммутации
38
39.
fсв (t )зависит от корней
характеристического
уравнения и начальных
условий
39
40.
Характеристическоеуравнение 3:
n
аnp аn 1p
n 1
... а1p а0 0
40
41.
а) если корниp1 , p 2 , ... , pn
уравнения 3 вещественные,
отрицательные и разные
41
42.
То тогдаfсв (t ) A1e
p1t
A 2e
p 2t
... Ane
pn t
42
43.
б) если корни уравнения 3вещественные,
отрицательные и
одинаковые, т.е.
p1 p 2 ... pn p
43
44.
То тогдаfсв (t ) ( A1 A 2t ... Ant
n 1
) e
pt
44
45.
в) если корни уравнения 3комплексные и попарно
сопряженные, т.е.
p1, 2 2 j св2
. . . . . . . . . . .
pn 1,n n j свn
45
46.
То тогдаfсв (t ) A 2e
A ne
2t
n t
сos( св2 t 2 ) ...
сos( свn t n )
46
47.
Где:A1 , A 2 , ... , An , 2 , ... , n
постоянные интегрирования,
определяемые начальными
условиями
47
48.
Где:2 , ... , n
коэффициенты затухания
свободных колебаний 1 с
48
49.
Где:св 2 , ... , свn
угловые частоты
свободных колебаний
рад
с
49
50.
Различают:а) независимые начальные
условия
i L (0 ) i L (0 )
и
uC ( 0 ) uC ( 0 )
50
51.
б) зависимые начальныеусловия
iС (0 ), uL (0 )
и другие величины
51
52.
в) принужденные значения,определяемые из расчета
установившегося режима
после коммутации
52
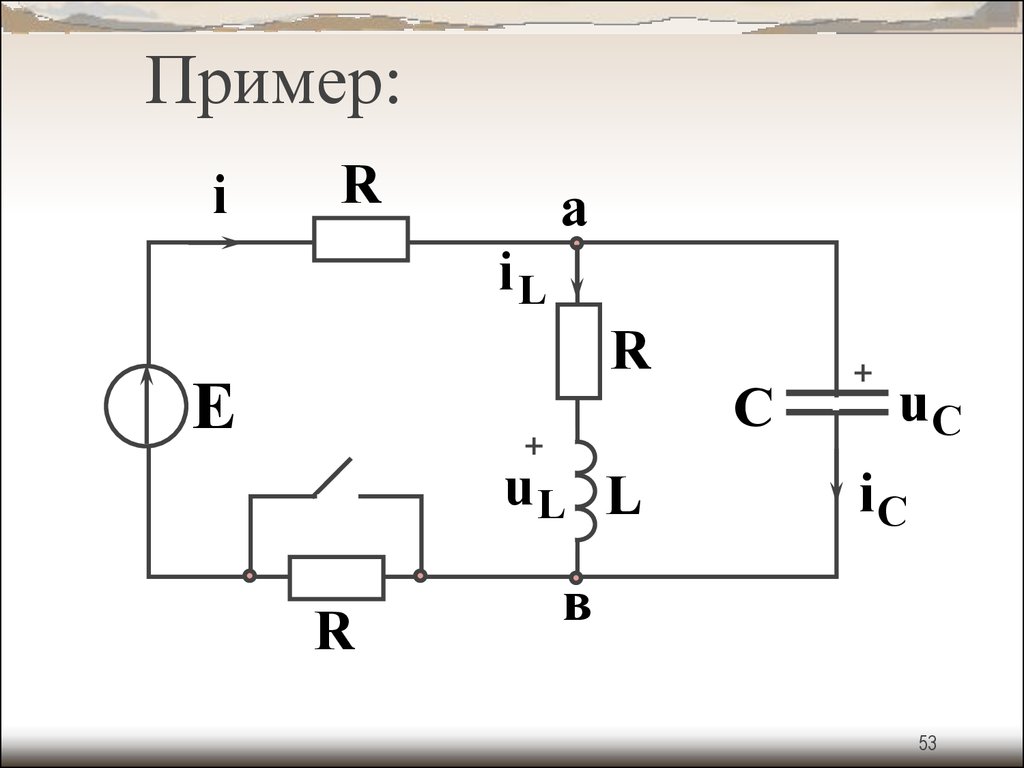
53.
Пример:i
R
а
iL
R
E
+
uL L
R
С
+
uC
iC
в
53
54.
Дано:E 300 В
R 100 Ом
Определить:
начальные условия и
принужденные составляющие
54
55.
а) независимые начальныеусловия
(схема до коммутации)
E
i L (0 )
1A
3R
uC (0 ) i L (0 )R 100 B
55
56.
б) зависимые начальныеусловия
(схема после
коммутации при
t 0 )
56
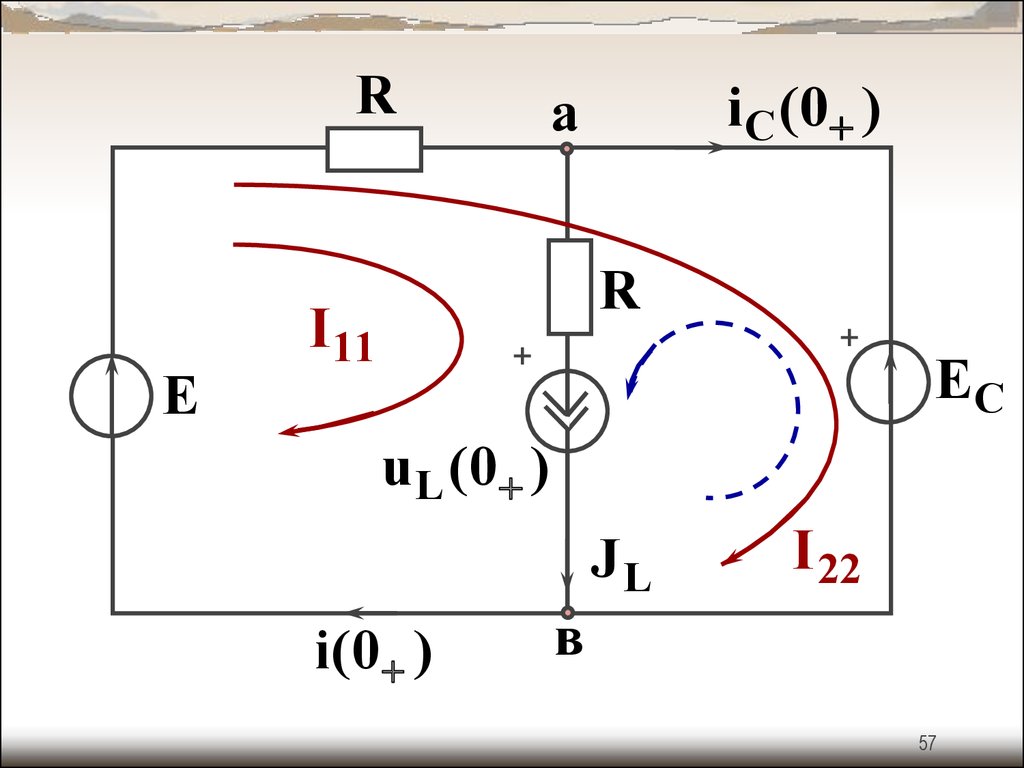
57.
RЕ
i C ( 0 )
а
R
I11
+
+
EC
u L (0 )
JL
i( 0 )
I 22
в
57
58.
J L i L (0 ) i L (0 ) 1 AEC uC (0 ) uC (0 ) 100 B
I11 J L 1 A
I 22R I11R E EC
58
59.
I 22E EC I11R
1A
R
i(0 ) I11 I 22 2 A
iC (0 ) I 22 1 A
59
60.
EC uL (0 ) R i L (0 )uL (0 ) EC R i L (0 ) 0
60
61.
в) принужденныесоставляющие
(схема после коммутации
при t = )
При постоянных
источниках: L – закоротка,
С – разрыв.
61
62.
i пр i LпрE
1.5 A
2R
uCпр R i Lпр 150 В
i Cпр 0
uLпр 0
62




















































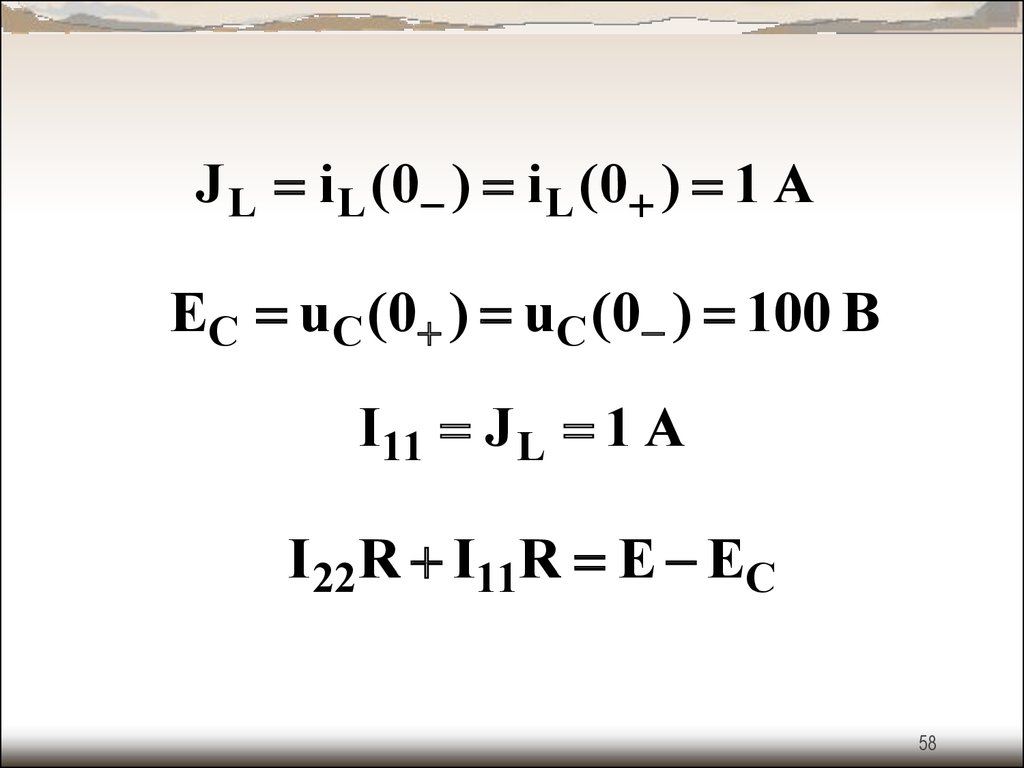
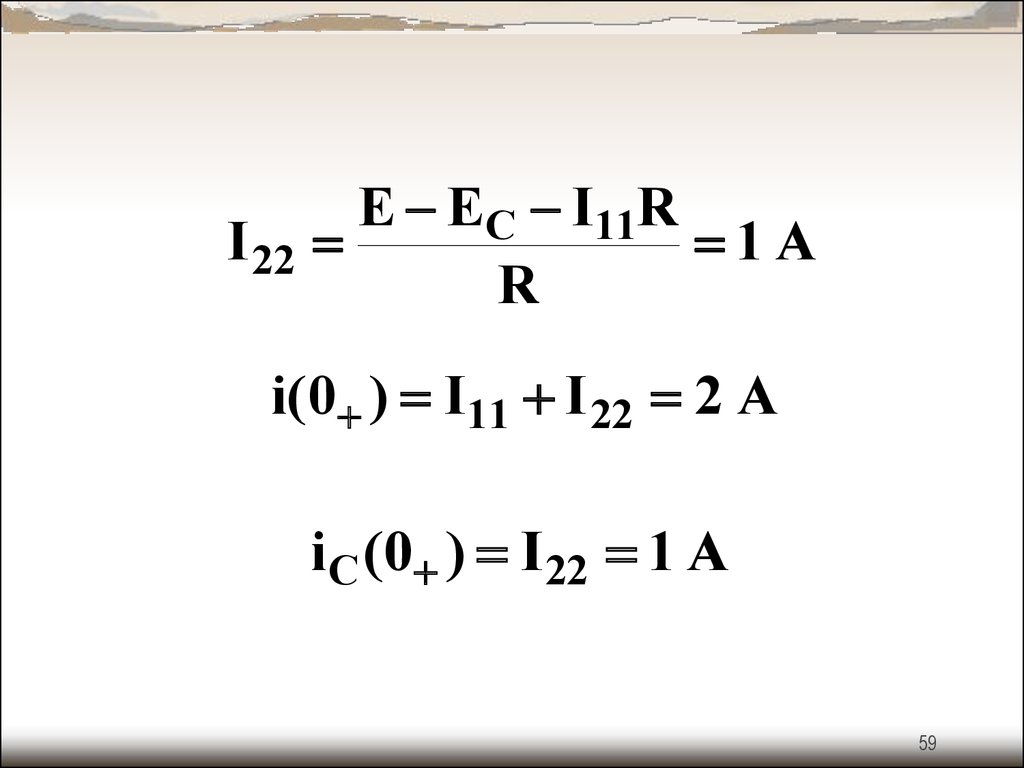



 electronics
electronics








