Similar presentations:
Задание № 15 - это несложная планиметрическая задача с практическим содержанием
1.
Задание № 15 - этонесложная
планиметрическая задача с
практическим
содержанием
2.
Рассмотрим какие темы используются в задачах №15 ОГЭ1 Вычисление длин и площадей
2 Подобие треугольников
3 Теорема Пифагора
4 Углы
5 Разные задачи
3.
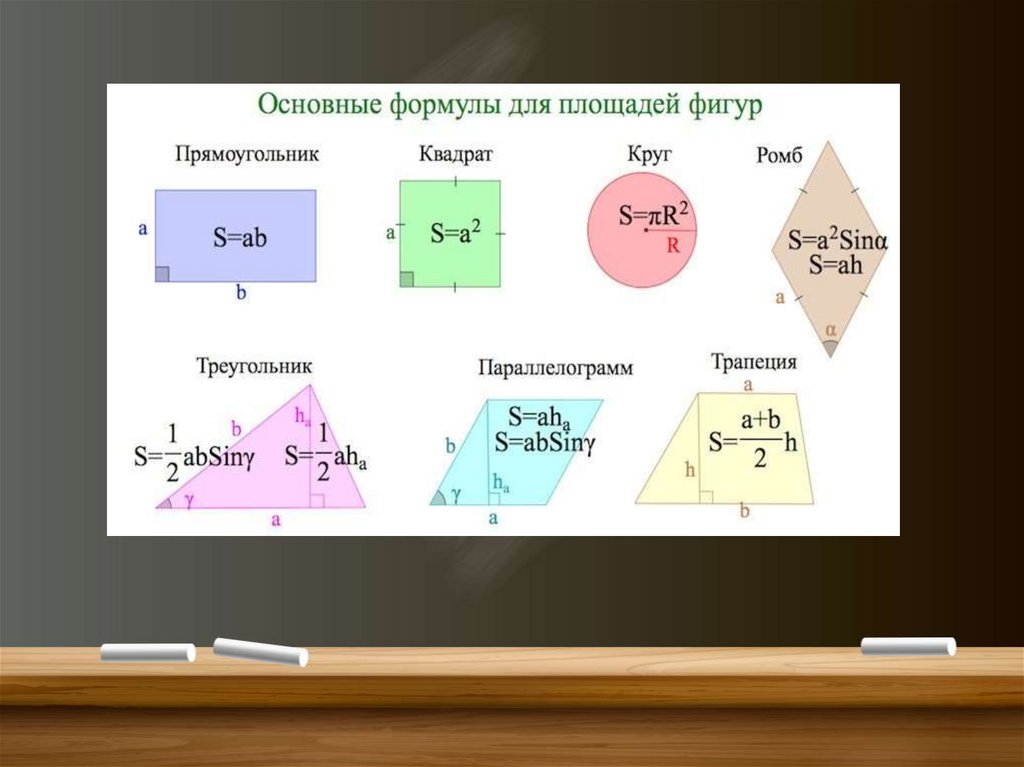
Тест на тему площади многоугольниковВыберите верные утверждения:
а) площадь прямоугольника равна произведению его
соседних сторон;
б) площадь прямоугольника равна квадрату его стороны;
в) площадь прямоугольника равна удвоенному
произведению двух его соседних сторон.
Закончите фразу: Площадь ромба равна половине
произведения…
а) его сторон;
б) его стороны и высоты, проведённой к этой стороне;
в) его диагоналей.
По формуле S=ah можно вычислить площадь:
а) параллелограмма;
б) треугольника;
в) прямоугольника.
Выберите верное утверждение:
Площадь прямоугольного треугольника равна:
а) половине произведения его стороны на какую-либо
высоту;
б) половине произведения его катетов;
в) произведению его стороны на проведённую к ней
высоту.
В треугольниках ABC и MNK . Отношение площадей
треугольников ABC и MNK равно:
а) AB*BC; б) AB*AC ; в) BC*AC
MN*NK
MN*MK
NK*MK
В треугольниках MNK и DOS высоты NE
и OT равны. Тогда
а) MN : PO; б) MK : PS; в) NK : OS.
Площадь трапеции ABCD с основаниями AB и CD и
высотой BH вычисляется по формуле:
а) S= AB:2*СD*ВН ;
б) S= (AB+BC):2*BH;
в) S=(AB+CD):2*BH
4.
5.
1.Найдите периметрпрямоугольного участка
земли, площадь которого
равна 800 м 2 и одна сторона
в 2 раза больше другой.
Ответ дайте в метрах.
Решение.
Пусть x м — ширина
участка, тогда длина —
2 x м. Так как площадь
прямоугольника равна
произведению его смежных
сторон,
то откуда х=20.
Р=(20+40)*2=120
Периметр прямоугольника
Ответ: 120.
2.Площадь прямоугольного земельного
участка равна 9 га, ширина участка равна
150 м. Найдите длину этого участка в
метрах.
Решение.
Переведем площадь участка в
квадратные метры: 9 га = 90 000 м2.
Площадь прямоугольника равна
произведению его смежных сторон.
Поэтому, длина участка равна:
90 000 : 150 = 600 м.
Ответ: 600.
2
Х
2х
90 000м
150 м
6.
3.Периметр квадрата равен160. Найдите площадь этого
квадрата.
Решение
Р=4а, а=40,
S=40*40=1600
4 . Дерево имеет в обхвате 120
см. Найдите примерную
площадь
поперечного сечения (в см2),
имеющего форму круга.
(Примите π≈ 3.)
Решение
2
С= 2 π r; r=20 см; S= πr
2
2
S=2*3*20 =1200 см
a
7.
Задачи из решу огэ8.
9.
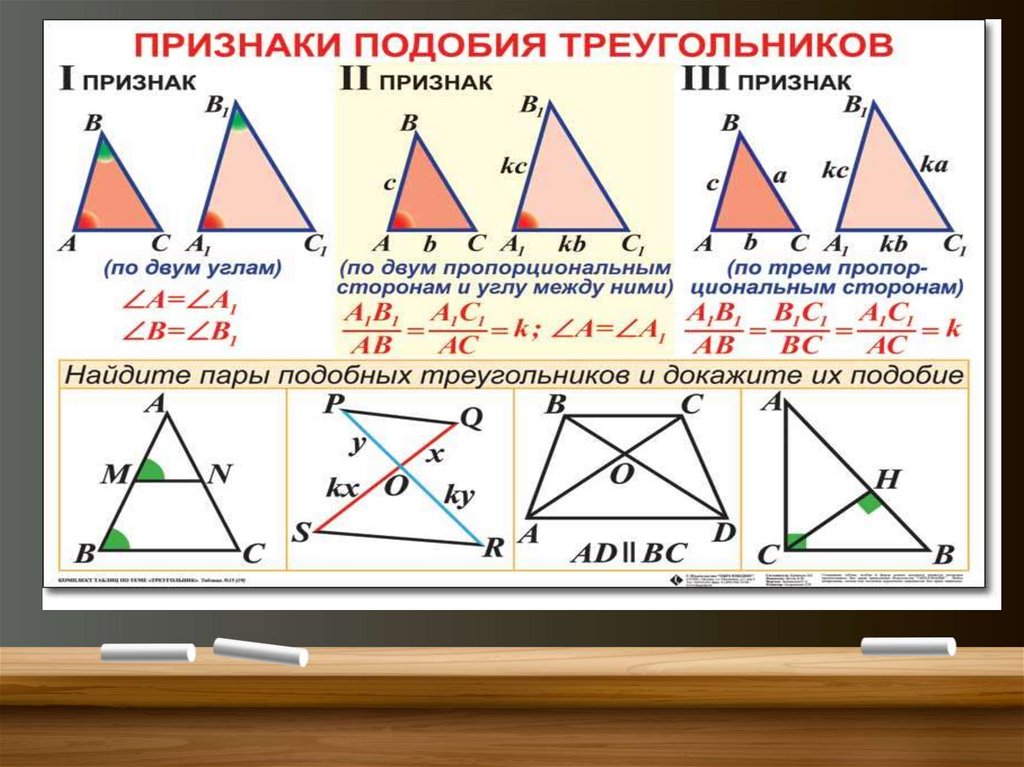
Тест «Подобные треугольники»Вариант
Отношением отрезков АВ и СD называется ____________________.
В треугольниках сходственными сторонами называются те стороны, которые ___________________.
Коэффициентом подобия треугольников называется отношение ______________.
Если АD – биссектриса угла АВС, то какая из указанных пропорций не удовлетворяет свойству
биссектрисы угла АВС
BD = DC
BD = АВ
BD = DC
а) AB AC
б) DC АС
в) AC AB
АВС А1В1С1. Сходственные стороны ВС и В1С1 соответственно равны 1,4 м и 56 см. Найдите
отношение периметров АВС и А1В1С1.
1
а) 2,5
б)40
в) 4
Какой должна быть прямая, проведенная через стороны треугольника, чтобы отсечь от него
треугольник, подобный данному?
а) перпендикулярной к какой-либо стороне
б) параллельной какой-либо стороне
в) проведенной произвольным образом
Отношение высот, проведенных к сходственным сторонам подобных треугольников, равно
_________________.
Квадрат коэффициента подобия 2х подобных треугольников равен..
а) отношению их сходственных сторон
б) отношению их площадей
в) отношению их периметров
10.
11.
Проектор полностью освещает экран A высотой 80 см,расположенный на расстоянии 250 см от проектора. На
каком наименьшем расстоянии (в сантиметрах) от
проектора нужно расположить экран B высотой 160 см,
чтобы он был полностью освещён, если настройки
проектора остаются неизменными?
Решение.
Заметим, что высота экрана, расположенного на
расстоянии 250 см, в 2 раза меньше высоты экрана,
расположенного на искомом расстоянии, значит, по
теореме о средней линии, искомое расстояние в два
раза больше первоначального экрана: 250·2 = 500.
12.
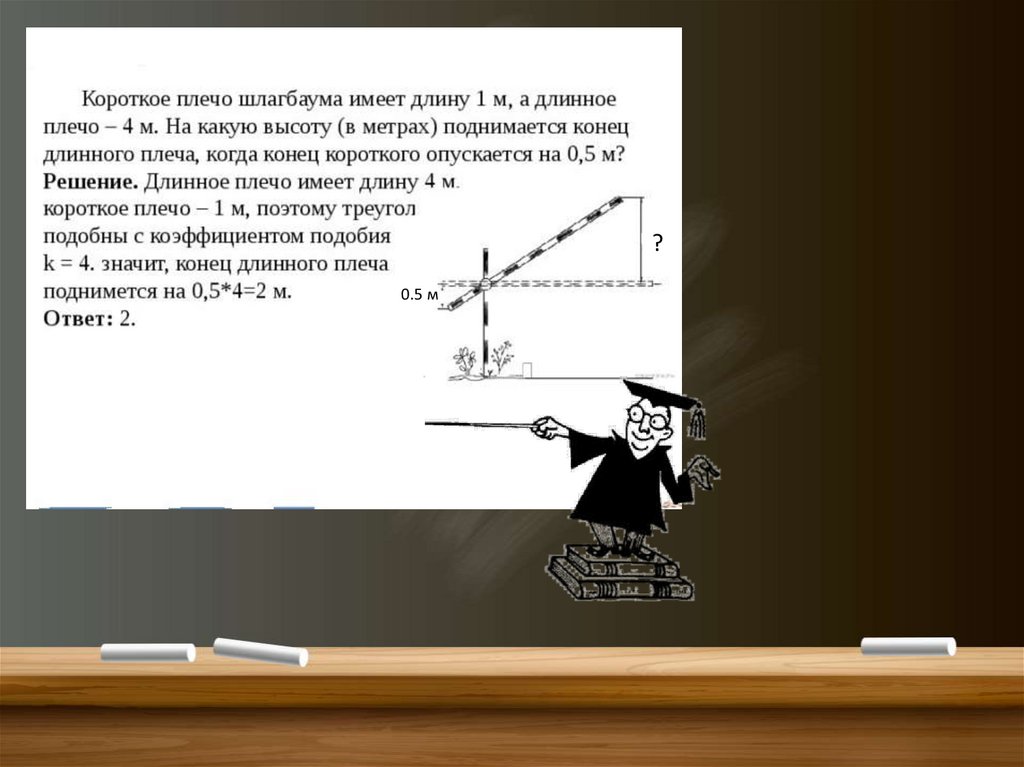
?0.5 м
13.
4 шага8 шагов
14.
Самостоятельная работа по теме подобные треугольники1.Треугольник АВС и MNP подобны.
Известно, что АВ = 3см, АС = 7см,
МР = 21см.
Найдите сторону MN.
2.Подобны ли треугольники, если стороны одного равны 2см, 4см,и 5см,а стороны
другого – 10дм, 15дм,и 20дм ?
3.На рисунке АО = 3см, ВО = 4см,
DO = 12см, ОС = 9см.Докажите, что треугольник АОВ и СОD подобны.
4.Отрезки АВ и СD пересекаются в точке О.
∠ АСО = ∠ ODB, АС = 5см, АО = 6см,
OD = 8см, DB = 10см.
Найдите СО и ОВ.
5.Найдите АС, если ВС =12см, NM = 6см,
CN = 4см, ВМ = NC.
15.
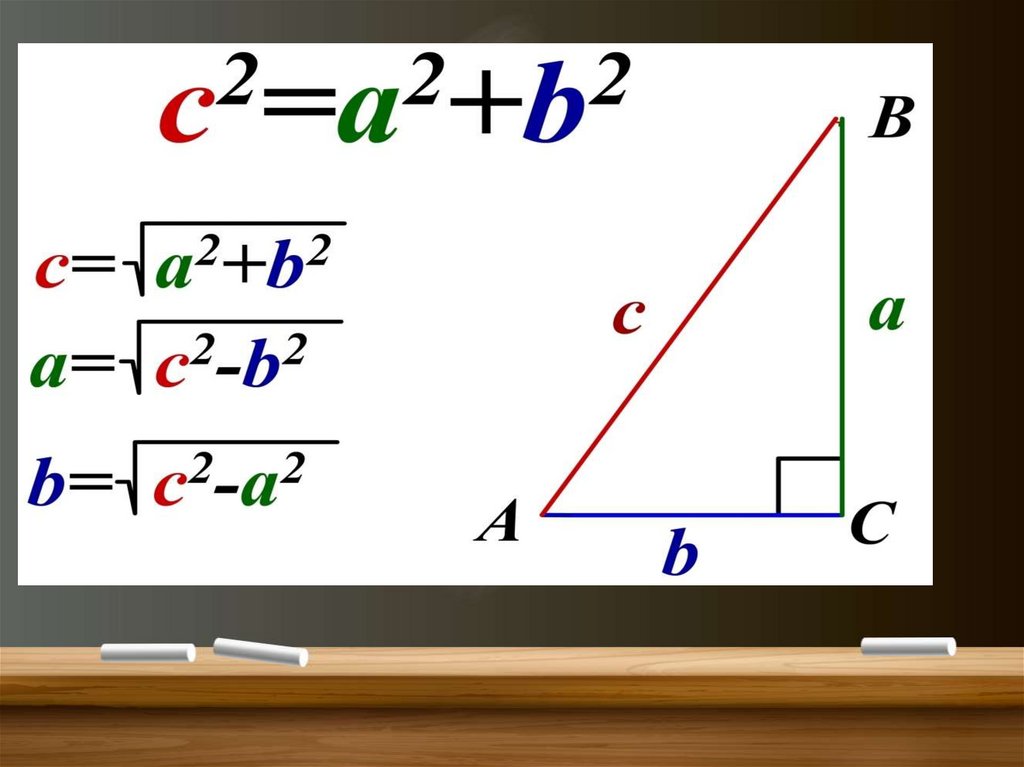
Тест по теме теорема ПифагораА1. Найдите гипотенузу
прямоугольного треугольника,
если его катеты равны 3см и
4см.
Варианты ответов:
1) 5
2) 6
3) 7
4) 8
Ответ: ___
А2. Найдите меньшую сторону
прямоугольника МКРД, если его смежные
стороны относятся как 3:2, а диагональ равна
5см.
Варианты ответов:
1) 2.5
2)
1.25
3) 3.125
4) 1.25
А3 Гипотенуза АВ прямоугольного треугольника АВС равна 4 см ,а
один из внешних углов А равен 150 градусам .Найти ВС.
Варианты ответов:
1)27
2) 2
3)3
4)40
Ответ ________
А4. Найдите сторону ромба АВСД, если ВД= 8см и
АС= 6см.
Варианты ответов:
1) 5
2) 8
3) 9
4) 25
Ответ: ___
16.
17.
Точка крепления троса, удерживающего флагшток ввертикальном положении, находится на высоте 3,2 метра от
земли. Длина троса равна 4 метра. Найдите расстояние от
основания флагштока до места крепления троса на
земле. Ответ дайте в метрах.
Решение:
Так как на чертеже - прямоугольный
треугольник,
применяем
теорему
Пифагора:
4² = 3,2² + x²
16 = 10,24 + x²
x² = 16 - 10,24
x² = 5,76
x = √5,76
x = 2,4 метра
Ответ: 2,4 метра
18.
3 Используя данные, приведенные на рисунке, найдите расстояние в метрах между пунктами A и B, расположенными на разныхберегах озера.
Решение.
По т Пифагора АВ=500 м
4 В 60м одна от другой растут две
сосны. Высота одной 31м,
а другой —6м. Найдите расстояние
между их верхушками.
Решение .
31-6=25 (м)
2
2
По т Пифагора 36 +25 =4225
4225
Ответ 65м
19.
Лестницу длиной 3 м прислонили к дереву.На какой высоте (в метрах) находится
верхний её конец, если нижний конец
отстоит от ствола дерева на 1,8 м?
Решение.
Задача сводится к нахождению катета прямоугольного
треугольника, по теореме Пифагора он равен:
Ответ: 2,4.
20.
Глубина крепостного рва равна 8 м, ширина5 м, а высота крепостной стены от ее
основания 20 м. Длина лестницы, по
которой можно взобраться на стену, на 2 м
больше, чем расстояние от края рва до
верхней точки стены (см. рис.). Найдите
длину лестницы.
Решение.
Расстояние AB — гипотенуза
прямоугольного треугольника с катетами
5 м и 20 − 8 = 12 м. Тем самым,
длина AB равна 13 м, а длина лестницы
равна 15 м.
Ответ: 15.
21.
Самостоятельная работа по теме «Теорема Пифагора»Вариант 1
1.Найдите гипотенузу, если катеты равны 2см и 5 см
2.Найдите катет, если гипотенуза равна 8см, а второй катет равен 3см
3.Найдите сторону ромба, если его диагонали равны 6см и 8см
4.Найдите диагональ прямоугольника со сторонами 5см и 4см
5.Найдите площадь равнобедренного треугольника, если боковая сторона
равна 7см, а основание – 4см
6.Найдите высоту равнобокой трапеции с основаниями 6см и 14см, если
боковая сторона равна 5см
22.
К сожалению не все девятиклассники умеютработать с круговым циферблатом
23.
Приходится иногда знакомится заново счасами..
1)На какой угол (в градусах) поворачивается
минутная стрелка пока часовая проходит
30
градуса
?
Решение.
Минутная стрелка движется в 12 раз быстрее
часовой, поэтому она пройдёт 360°.
Примечание.
Существенно, что циферблат предполагается 12часовым.
2) Какой угол (в градусах)
образуют минутная и часовая
стрелки часов в 18:00?
Найдите угол, который образуют
минутная и часовая стрелки часов
в 17:00. Ответ дайте в градусах.
24.
3)Сколько спиц в колесе, в котором угол между любымисоседними спицами равен 18°?
Решение.
Колесо представляет собой круг. Количество спиц
совпадает с количеством секторов на которые ими оно
делится. Так как полный угол равен 360°, а угол между
спицами равен 18°, имеем:
Поэтому спиц в
колесе 20 штук.
Ответ: 20.
4) На сколько градусов повернется Земля
вокруг своей оси за 7 часов?
Решение.
За сутки Земля совершает полный оборот, то
есть поворачивается на 360°.
Следовательно, за один час Земля
поворачивается на 360° : 24 = 15°. Получаем,
что за 7 часов Земля поворачивается на 7 ·
15° = 105
25.
Разные задачи являются прототипами других задач №15(задачи на т.Пифагора, углы и т.д.)
Встречаются также задачи такого типа:
1) Сколько всего осей
симметрии имеет фигура,
изображённая на рисунке
Решение.
Ось симметрии данной
фигуры — биссектриса ,
проходящая через
вершину звезды. Данная
фигура имеет 5 осей
симметрии.
Ответ: 5.
2)Обхват ствола секвойи
равен 4,8 м. Чему равен
его диаметр (в метрах)?
Ответ округлите до
десятых.
Решение.
Длина окружности
выражается формулой С=2ПD
D
1.5 м
26.
ВыводыЗадача №15 несложная планиметрическая
задача с практическим содержанием. Решая
и отрабатывая её на уроках мы охватываем
многие темы и задачи ,которые представлены
в ОГЭ.
27.
Интернет ресурсы и литература:https://egemaximum.ru/podobnye-treugolniki/
https://nsportal.ru/shkola/geometriya/library/2017/
08/11/test-ploshchadi-mnogougolnikov-8-klass
https://урок.рф/library/test_po_geometrii_teorema_
pifagora8_klass_154532.html
https://math-oge.sdamgia.ru
http://www.fipi.ru/content/otkrytyy-bank-zadaniyoge
http://emmom.ru/books/prakt.pdf
И.В.Ященко ОГЭ 2019 математика
36 вариантов
























 mathematics
mathematics








