Электрические цепи постоянного тока. Лекция 1

1.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
1

2.

centennialbulb.org
2

3.

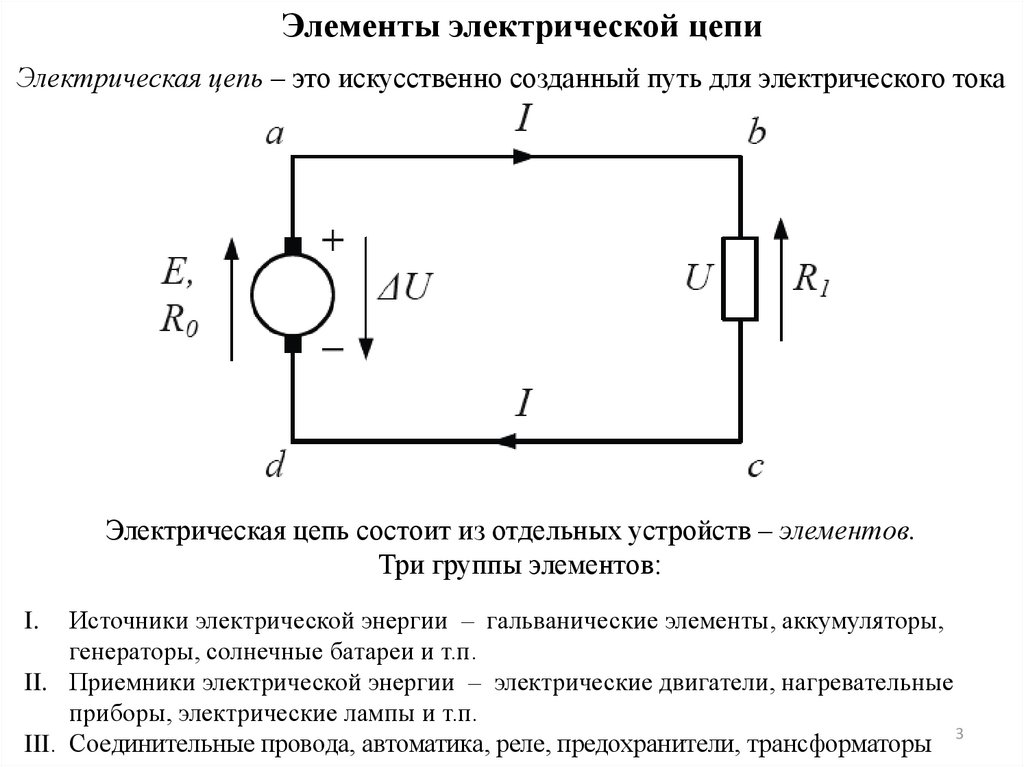
Элементы электрической цепи
Электрическая цепь – это искусственно созданный путь для электрического тока
Электрическая цепь состоит из отдельных устройств – элементов.
Три группы элементов:
Источники электрической энергии – гальванические элементы, аккумуляторы,
генераторы, солнечные батареи и т.п.
II. Приемники электрической энергии – электрические двигатели, нагревательные
приборы, электрические лампы и т.п.
III. Соединительные провода, автоматика, реле, предохранители, трансформаторы 3
I.

4.

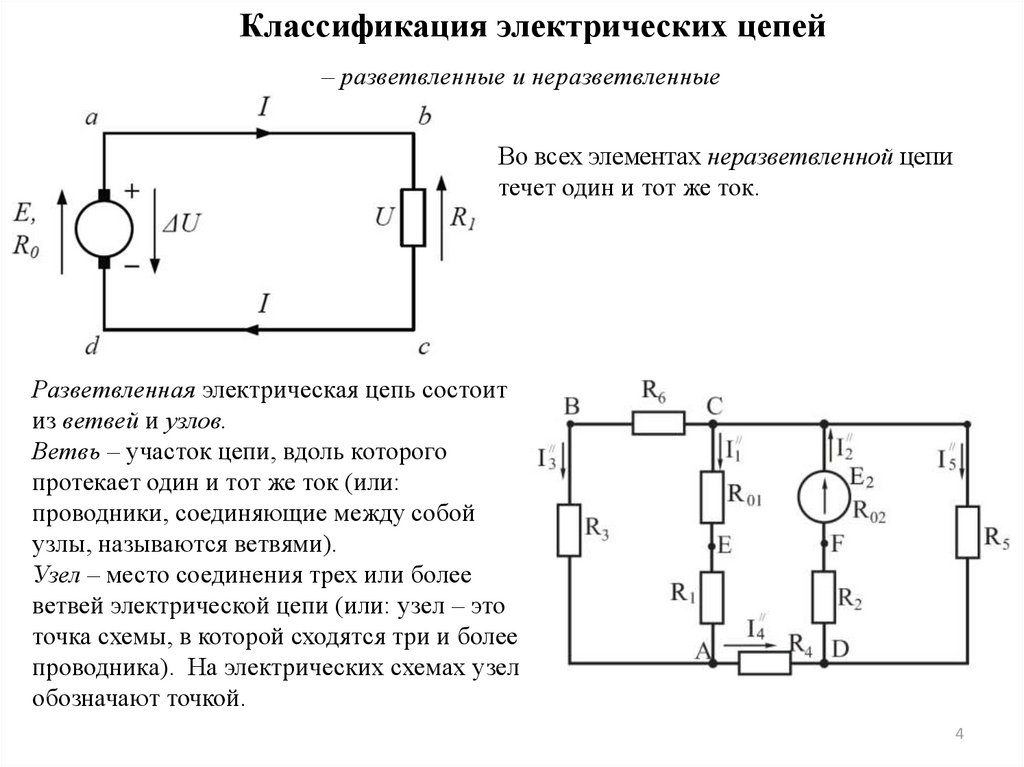
Классификация электрических цепей
– разветвленные и неразветвленные
Во всех элементах неразветвленной цепи
течет один и тот же ток.
Разветвленная электрическая цепь состоит
из ветвей и узлов.
Ветвь – участок цепи, вдоль которого
протекает один и тот же ток (или:
проводники, соединяющие между собой
узлы, называются ветвями).
Узел – место соединения трех или более
ветвей электрической цепи (или: узел – это
точка схемы, в которой сходятся три и более
проводника). На электрических схемах узел
обозначают точкой.
4

5.

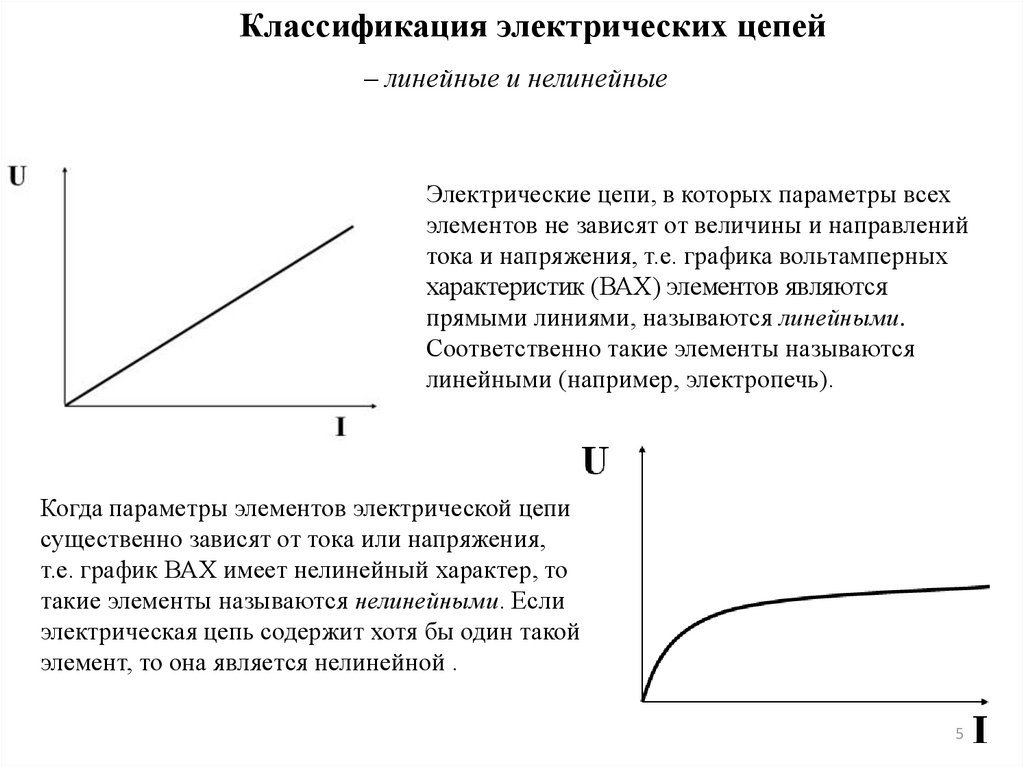
Классификация электрических цепей
– линейные и нелинейные
Электрические цепи, в которых параметры всех
элементов не зависят от величины и направлений
тока и напряжения, т.е. графика вольтамперных
характеристик (ВАХ) элементов являются
прямыми линиями, называются линейными.
Соответственно такие элементы называются
линейными (например, электропечь).
Когда параметры элементов электрической цепи
существенно зависят от тока или напряжения,
т.е. график ВАХ имеет нелинейный характер, то
такие элементы называются нелинейными. Если
электрическая цепь содержит хотя бы один такой
элемент, то она является нелинейной .
5

6.

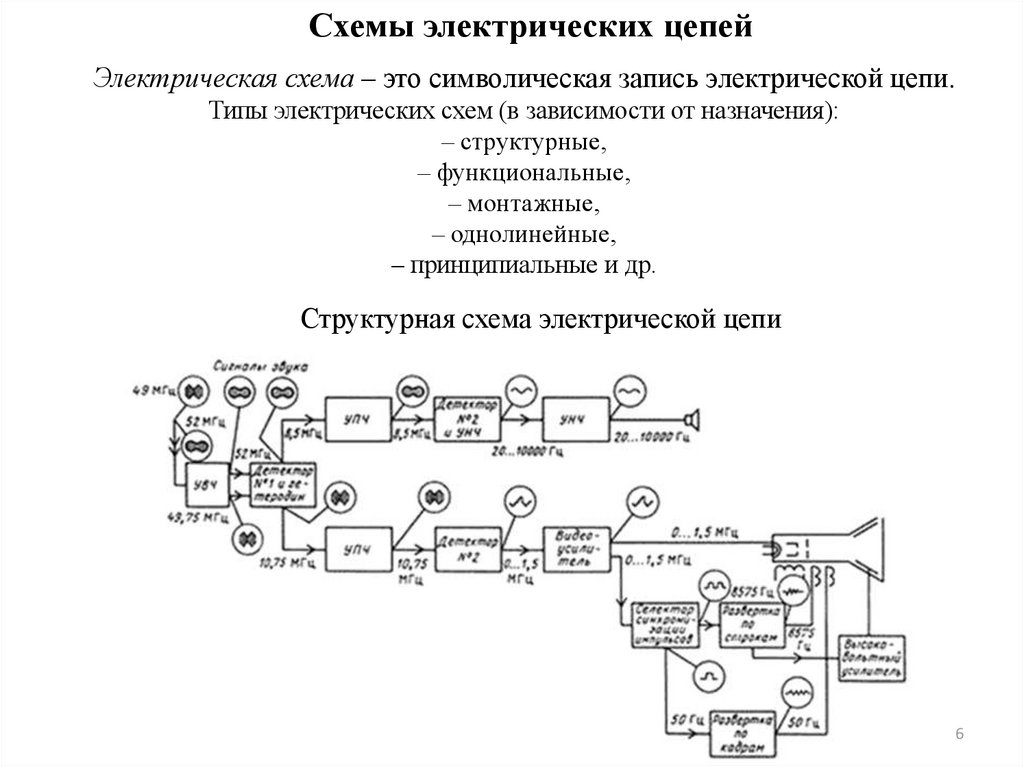
Схемы электрических цепей
Электрическая схема – это символическая запись электрической цепи.
Типы электрических схем (в зависимости от назначения):
– структурные,
– функциональные,
– монтажные,
– однолинейные,
– принципиальные и др.
Структурная схема электрической цепи
6

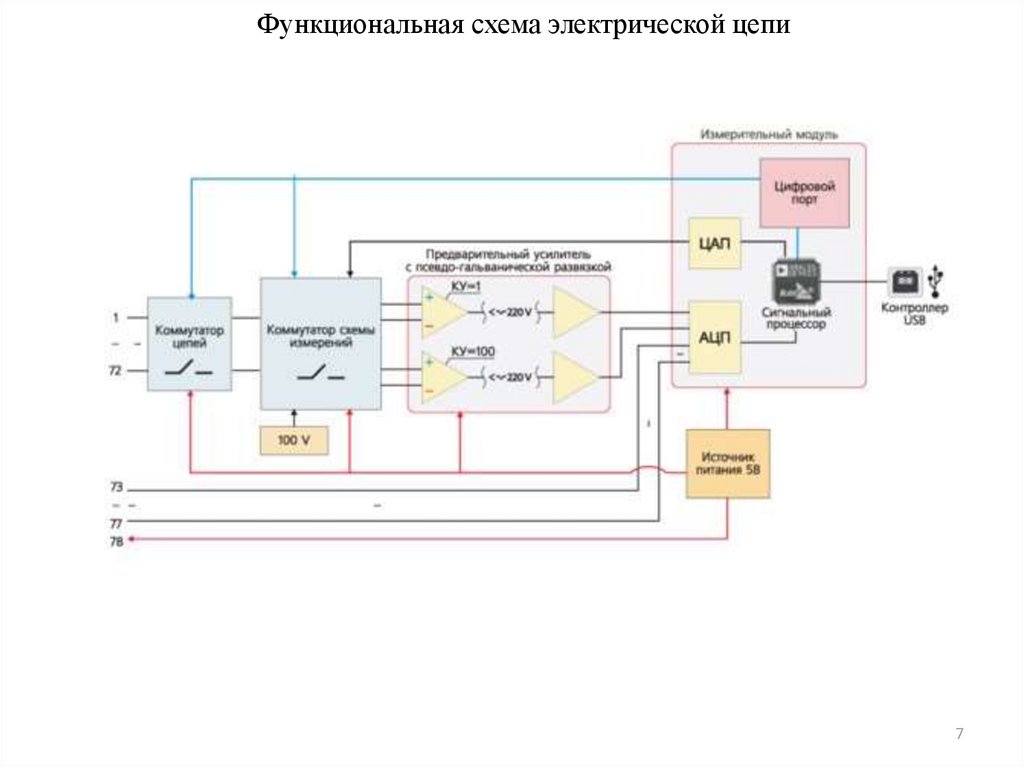
7. Функциональная схема электрической цепи

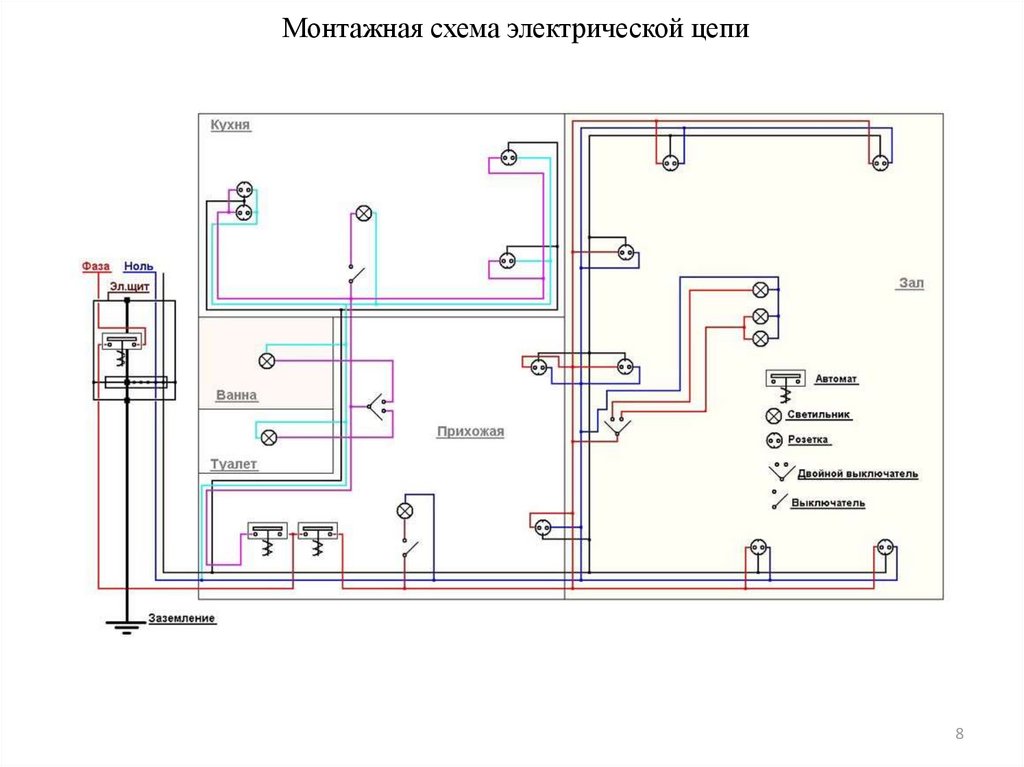
7

8. Монтажная схема электрической цепи

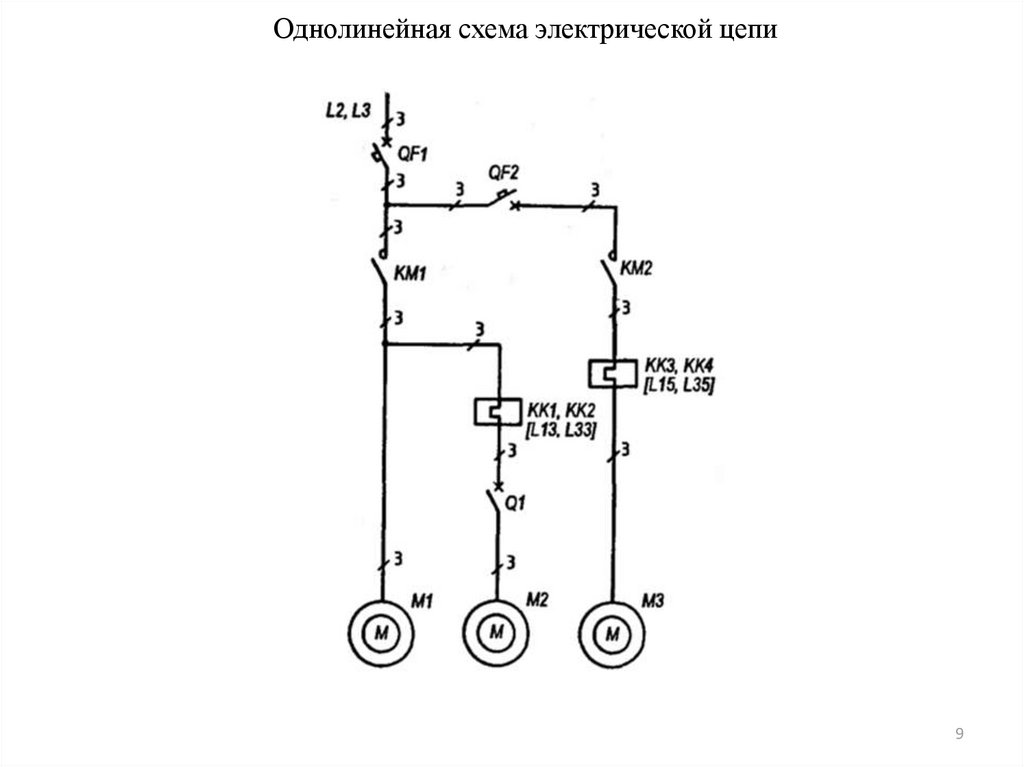
8

9. Однолинейная схема электрической цепи

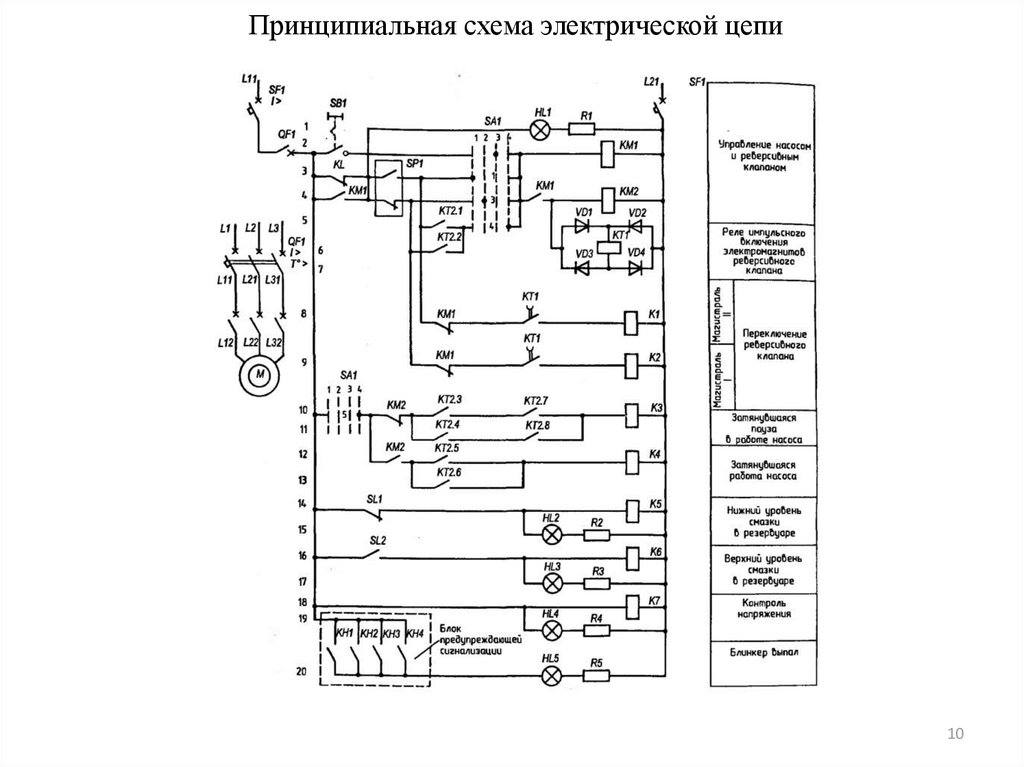
9

10. Принципиальная схема электрической цепи

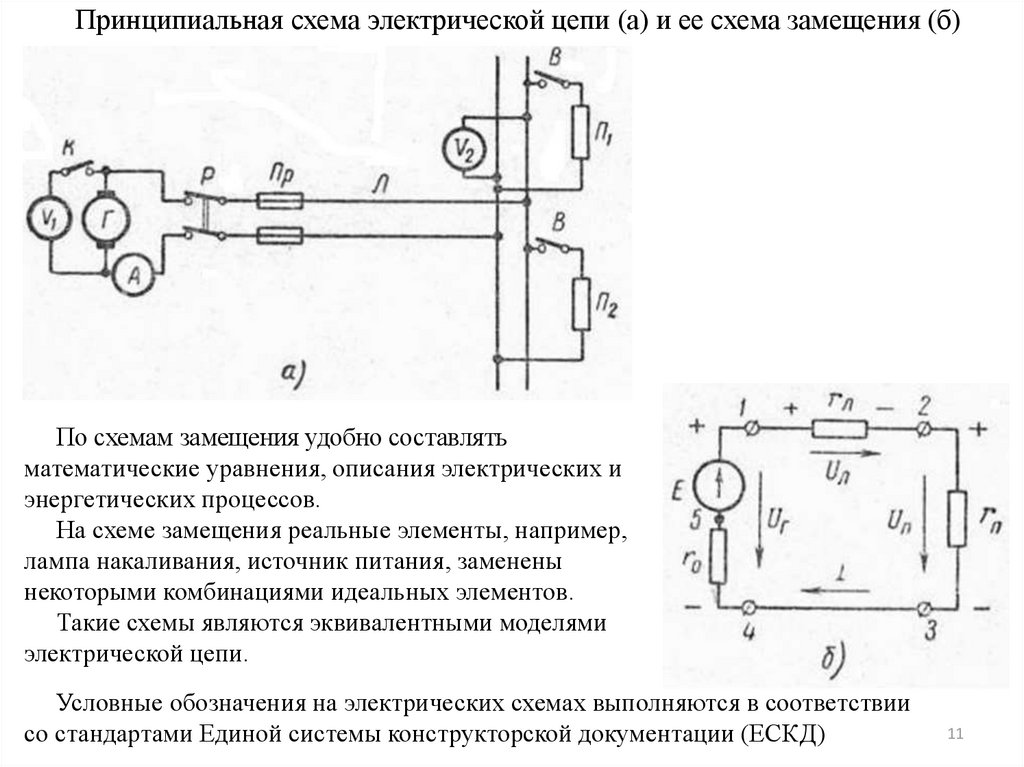
10

11. Принципиальная схема электрической цепи (а) и ее схема замещения (б)

По схемам замещения удобно составлять
математические уравнения, описания электрических и
энергетических процессов.
На схеме замещения реальные элементы, например,
лампа накаливания, источник питания, заменены
некоторыми комбинациями идеальных элементов.
Такие схемы являются эквивалентными моделями
электрической цепи.
Условные обозначения на электрических схемах выполняются в соответствии
со стандартами Единой системы конструкторской документации (ЕСКД)
11

12.

Основные понятия и определения
Электрический ток
Полный электрический ток – это направленное движение носителей заряда под
действием электрического поля.
Количественная оценка электрического тока – сила тока.
Сила тока, или ток, численно равна количеству электричества, проходящего через
поперечное сечение проводника в единицу времени:
Δq
i
Δt
1Кл
I 1А
1с
Чтобы получить силу тока в 1 А, через поперечное сечение проводника должны пройти
6∙1000000000000000000 (6∙1018 ) электронов
Ток называется постоянным, если он не
изменяется со временем:
q
I
t
За положительное направление тока принимается направление, в котором движутся
положительные заряды, от «+» к «–».
Силу тока измеряют амперметром, его включают последовательно в электрическую цепь
12

13.

Основные понятия и определения
Электродвижущая сила (э.д.с.)
Любая электрическая цепь состоит из внешнего и
внутреннего участков.
Внутренний участок включает в себя источник,
внешний – нагрузку и линию.
Э.д.с. Е численно равна работе, которую совершают сторонние силы при
перемещении единичного положительного заряда внутри источника или сам
источник, проводя единичный положительный заряд по замкнутой цепи.
1 Дж
Е
1В
1Кл
Действием э.д.с. источника обеспечивается определенная разность потенциалов Δφ на
его зажимах.
Зажим с более низким потенциалом называется отрицательным, обозначается «–»,
зажим с более высоким потенциалом называется положительным, обозначается «+».
Направление тока внутри источника совпадает с направлением э.д.с., то есть от «–» к
«+». Во внешней цепи ток направлен от «+» к «–», то есть от точки с более высоким
13
потенциалом к точке с более низким потенциалом.

14.

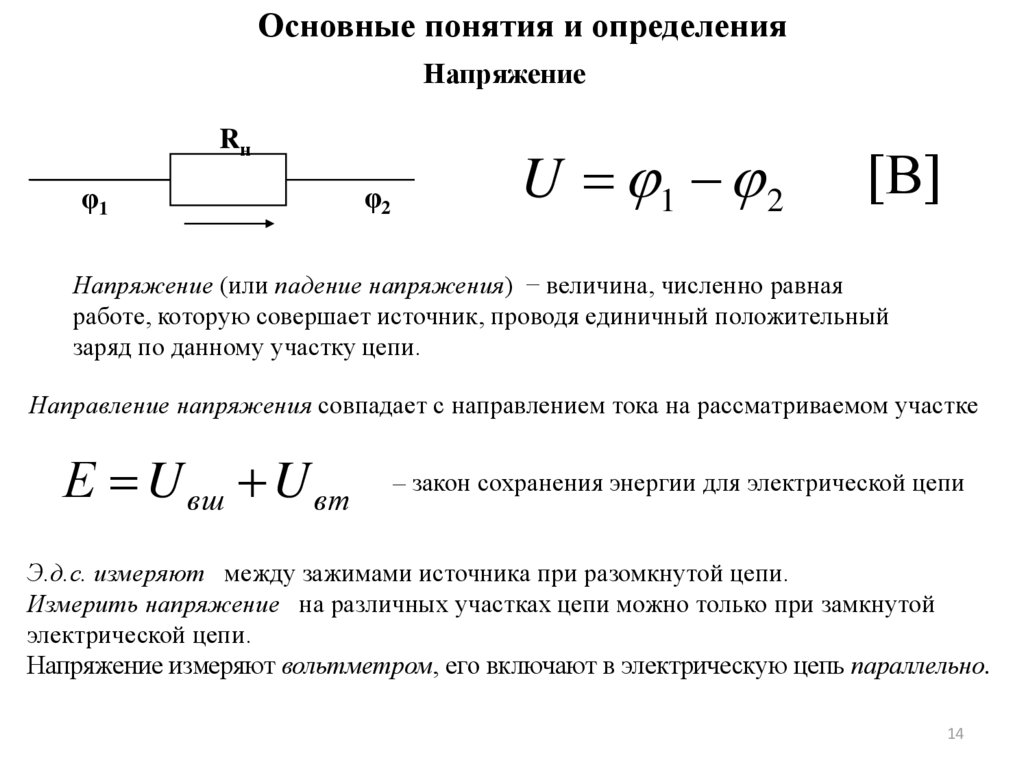
Основные понятия и определения
Напряжение
Rн
φ1
φ2
U 1 2
[В]
Напряжение (или падение напряжения) − величина, численно равная
работе, которую совершает источник, проводя единичный положительный
заряд по данному участку цепи.
Направление напряжения совпадает с направлением тока на рассматриваемом участке
Е U вш U вт
– закон сохранения энергии для электрической цепи
Э.д.с. измеряют между зажимами источника при разомкнутой цепи.
Измерить напряжение на различных участках цепи можно только при замкнутой
электрической цепи.
Напряжение измеряют вольтметром, его включают в электрическую цепь параллельно.
14

15.

Основные понятия и определения
Сопротивление
При наличии электрического тока в проводниках движущиеся свободные
электроны сталкиваются с ионами кристаллической решетки, то есть испытывают
противодействие своему движению. Это противодействие количественно
оценивается сопротивлением цепи R:
l
R
S
ρ – удельное сопротивление проводника
[Ом]
Ом мм 2
м
l – длина проводника [м]
S – площадь поперечного сечения проводника [м2]
15

16.

Активные и пассивные элементы
Активные элементы отдают электроэнергию в электрическую цепь − источники
Пассивные элементы ее потребляют − соединительные провода и электроприемники
Пассивным элементом при определенных условиях можно пренебречь.
Активным элементом пренебречь нельзя
К пассивным элементам относятся следующие идеализированные элементы:
1) Резистор, или сопротивление R
R
Свойство − необратимое рассеивание энергии.
Единица измерения [Ом].
2) Индуктивность L
L
Свойство − накапливает энергию магнитного поля.
Единица измерения генри [Гн].
3) Емкость С
C
Свойство − накапливает энергию электрического поля.
Единица измерения фарад [Ф].
К активным элементам относятся следующие идеализированные элементы:
Источник напряжения Rвт 0
Источник тока
Rвт
E
J
16

17.

Цепи постоянного тока − это электрические цепи, в которых ток не меняет своего
направления, то есть полярность источников э.д.с. в которых постоянна.
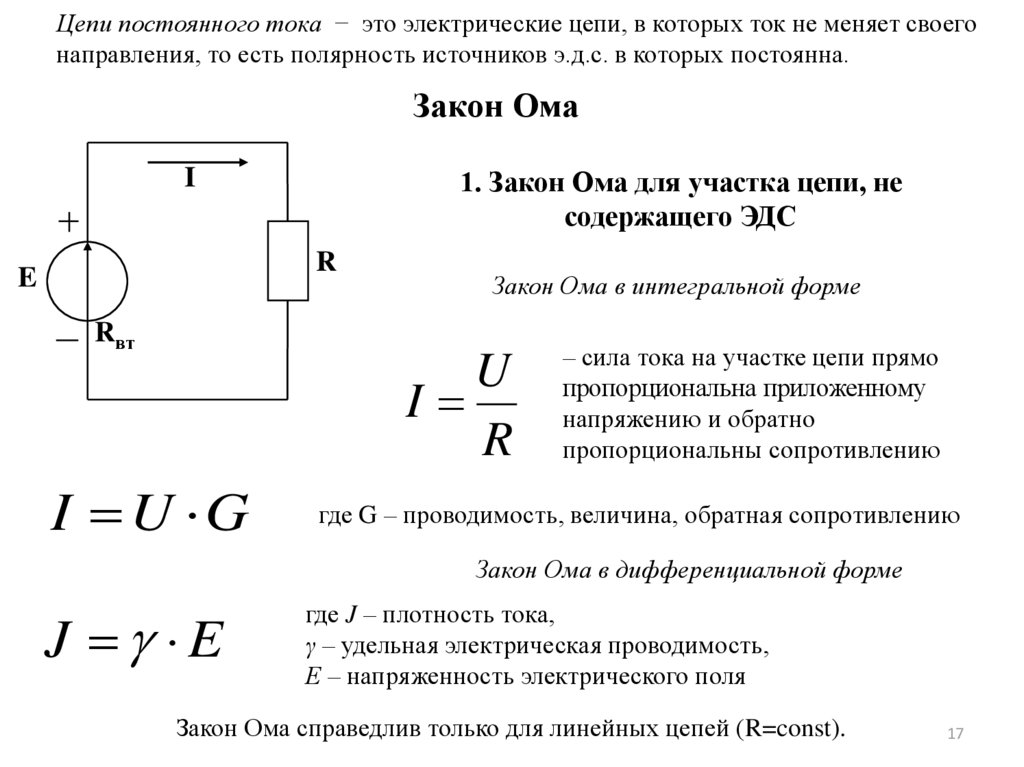
Закон Ома
1. Закон Ома для участка цепи, не
содержащего ЭДС
I
R
E
Rвт
Закон Ома в интегральной форме
U
I
R
I U G
– сила тока на участке цепи прямо
пропорциональна приложенному
напряжению и обратно
пропорциональны сопротивлению
где G – проводимость, величина, обратная сопротивлению
Закон Ома в дифференциальной форме
J E
где J – плотность тока,
γ – удельная электрическая проводимость,
Е – напряженность электрического поля
Закон Ома справедлив только для линейных цепей (R=const).
17

18.

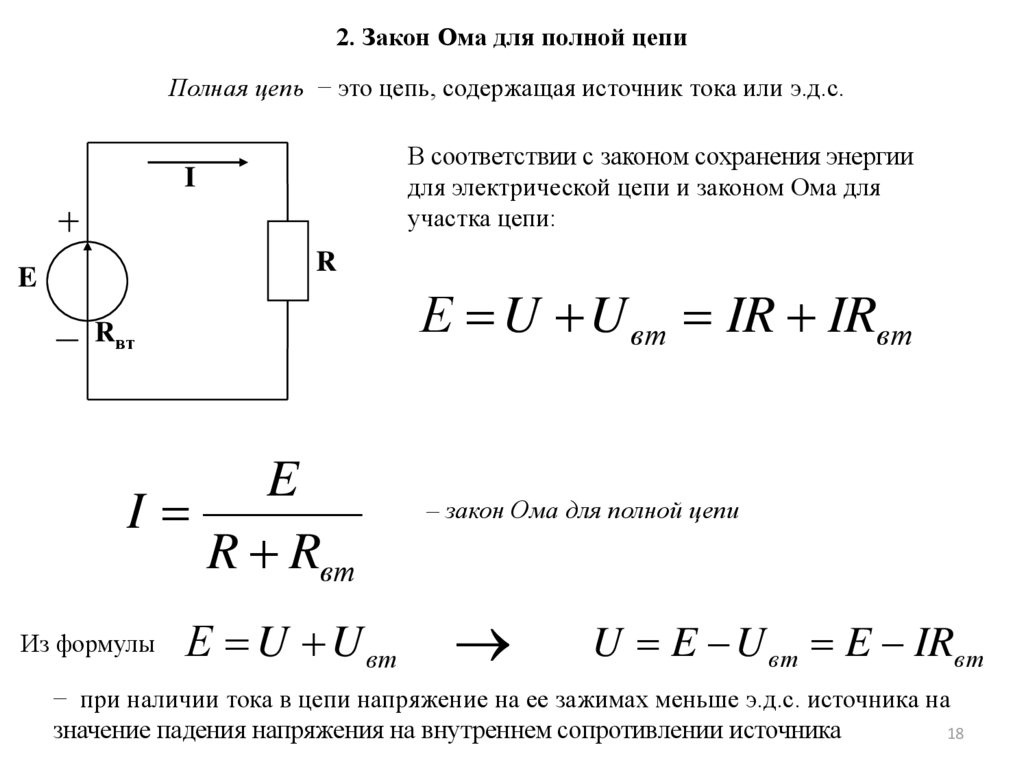
2. Закон Ома для полной цепи
Полная цепь − это цепь, содержащая источник тока или э.д.с.
В соответствии с законом сохранения энергии
для электрической цепи и законом Ома для
участка цепи:
I
R
E
Е U U вт IR IRвт
Rвт
E
I
R Rвт
Из формулы
Е U U вт
– закон Ома для полной цепи
U E U вт E IRвт
− при наличии тока в цепи напряжение на ее зажимах меньше э.д.с. источника на
значение падения напряжения на внутреннем сопротивлении источника
18

19.

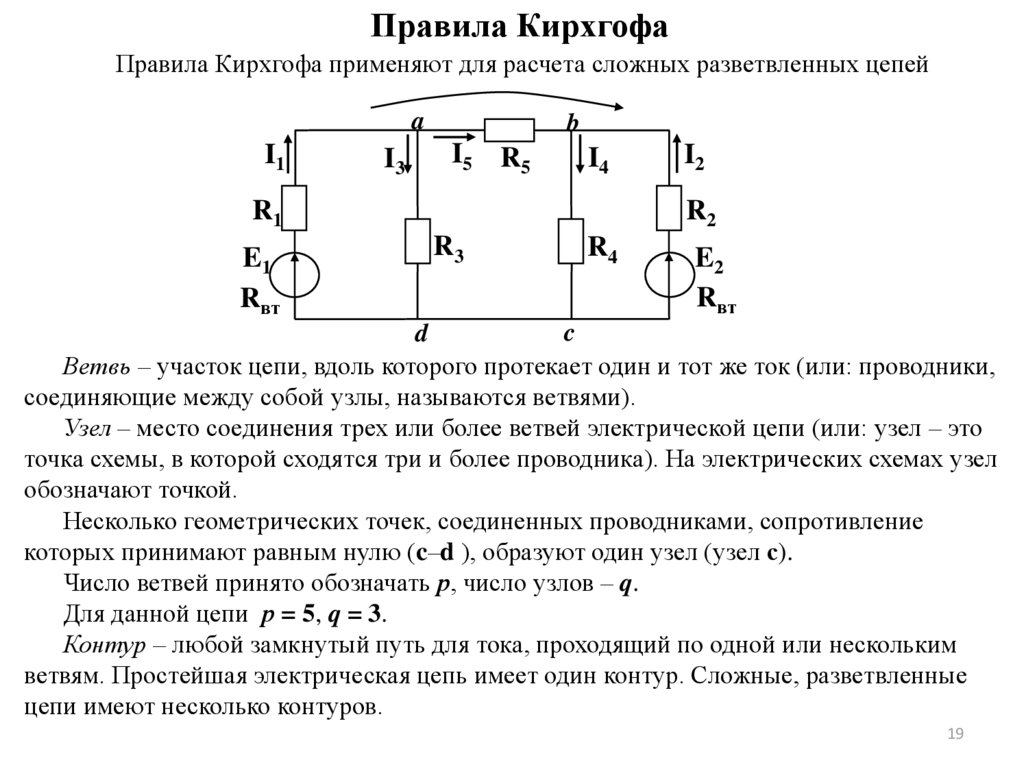
Правила Кирхгофа
Правила Кирхгофа применяют для расчета сложных разветвленных цепей
a
I1
I3
b
I5 R 5
I4
R1
E1
Rвт
I2
R2
R3
R4
E2
Rвт
c
d
Ветвь – участок цепи, вдоль которого протекает один и тот же ток (или: проводники,
соединяющие между собой узлы, называются ветвями).
Узел – место соединения трех или более ветвей электрической цепи (или: узел – это
точка схемы, в которой сходятся три и более проводника). На электрических схемах узел
обозначают точкой.
Несколько геометрических точек, соединенных проводниками, сопротивление
которых принимают равным нулю (c–d ), образуют один узел (узел с).
Число ветвей принято обозначать р, число узлов – q.
Для данной цепи р = 5, q = 3.
Контур – любой замкнутый путь для тока, проходящий по одной или нескольким
ветвям. Простейшая электрическая цепь имеет один контур. Сложные, разветвленные
цепи имеют несколько контуров.
19

20.

Правила Кирхгофа
Так как сложная цепь состоит из узлов и ветвей, поэтому и правил Кирхгофа два:
одно для узлов, второе для ветвей (контуров)
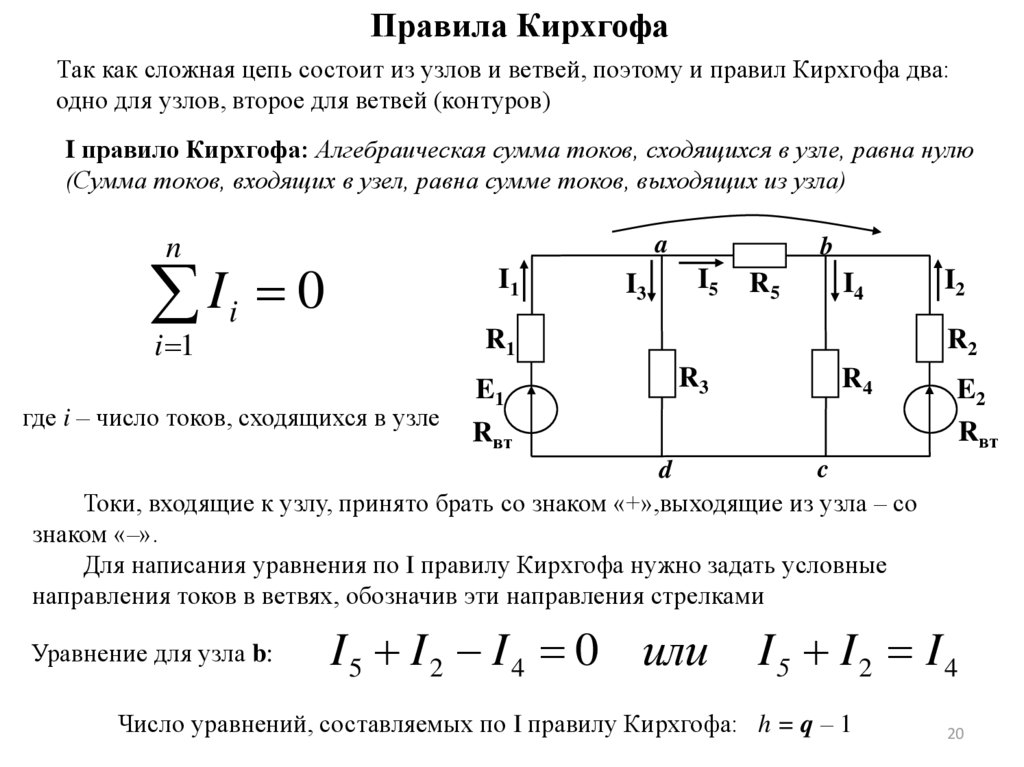
I правило Кирхгофа: Алгебраическая сумма токов, сходящихся в узле, равна нулю
(Сумма токов, входящих в узел, равна сумме токов, выходящих из узла)
a
n
Ii 0
I1
i 1
I3
b
I5
R5
I4
R1
где i – число токов, сходящихся в узле
E1
I2
R2
R3
R4
Rвт
E2
Rвт
c
d
Токи, входящие к узлу, принято брать со знаком «+»,выходящие из узла – со
знаком «–».
Для написания уравнения по I правилу Кирхгофа нужно задать условные
направления токов в ветвях, обозначив эти направления стрелками
Уравнение для узла b:
I 5 I 2 I 4 0 или
I5 I2 I4
Число уравнений, составляемых по I правилу Кирхгофа: h = q – 1
20

21.

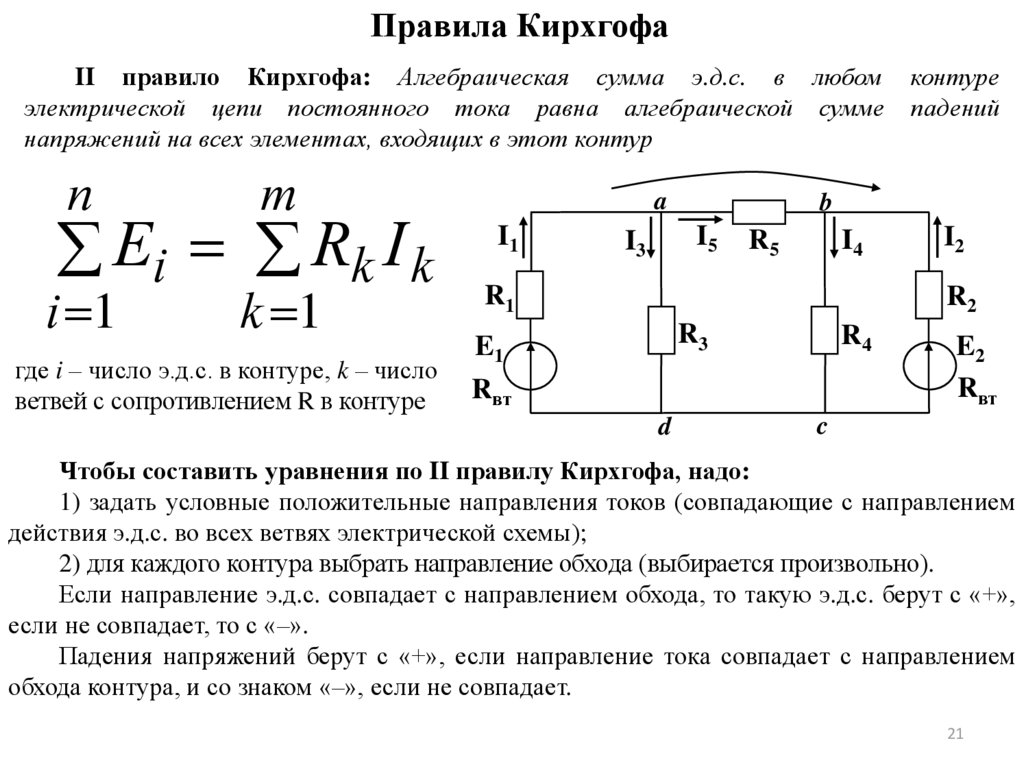
Правила Кирхгофа
II правило Кирхгофа: Алгебраическая сумма э.д.с. в любом контуре
электрической цепи постоянного тока равна алгебраической сумме падений
напряжений на всех элементах, входящих в этот контур
n
m
Еi Rk I k
i 1
k 1
где i – число э.д.с. в контуре, k – число
ветвей с сопротивлением R в контуре
a
I1
b
I5
I3
R5
I4
R1
I2
R2
R3
E1
R4
Rвт
d
E2
Rвт
c
Чтобы составить уравнения по II правилу Кирхгофа, надо:
1) задать условные положительные направления токов (совпадающие с направлением
действия э.д.с. во всех ветвях электрической схемы);
2) для каждого контура выбрать направление обхода (выбирается произвольно).
Если направление э.д.с. совпадает с направлением обхода, то такую э.д.с. берут с «+»,
если не совпадает, то с «–».
Падения напряжений берут с «+», если направление тока совпадает с направлением
обхода контура, и со знаком «–», если не совпадает.
21

22.

II правило Кирхгофа: Алгебраическая сумма э.д.с. в любом контуре
электрической цепи постоянного тока равна алгебраической сумме падений
напряжений на всех элементах, входящих в этот контур
a
n
m
Еi Rk I k
i 1
k 1
I1
b
I5
I3
R5
I4
R1
I2
R2
R3
E1
R4
Rвт
d
E2
Rвт
c
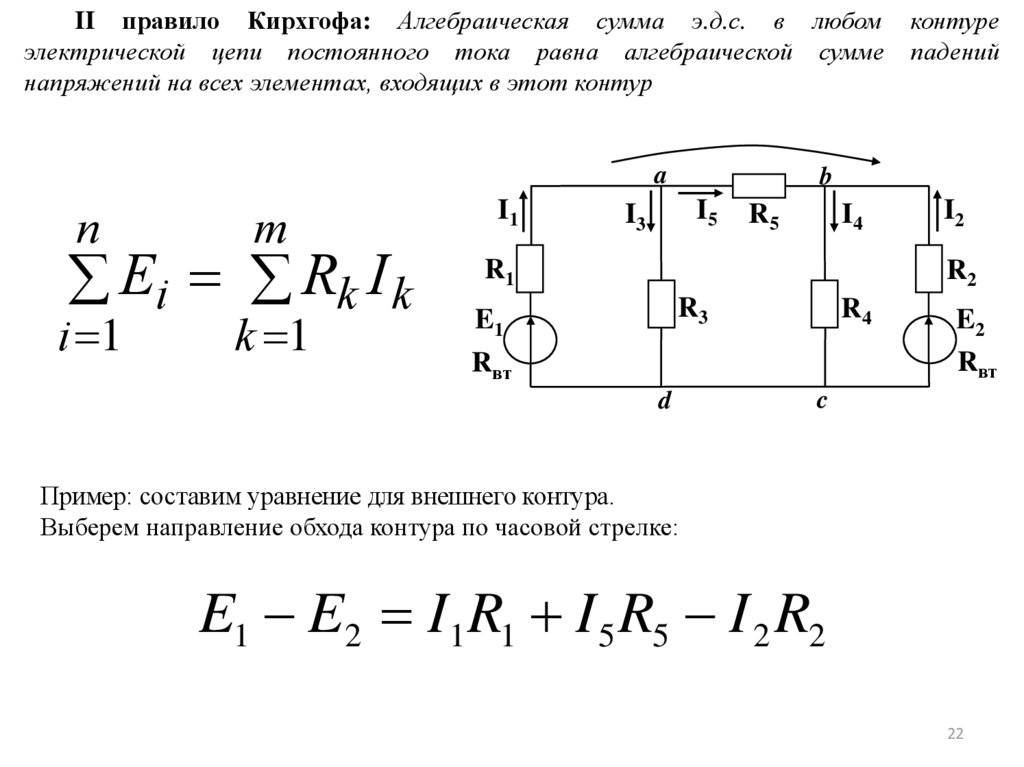
Пример: составим уравнение для внешнего контура.
Выберем направление обхода контура по часовой стрелке:
E1 E2 I1 R1 I 5 R5 I 2 R2
22

23.

Для простейшей одноконтурной схемы, состоящей из источника э.д.с. и потребителя R,
можно записать:
E RI U R
Но если вместо э.д.с. Е при обходе контура взять напряжение U на зажимах источника
э.д.с., которое направлено противоположно выбранному направлению обхода по
часовой стрелке, то в результате получим
U R U 0 или U U R
II правило Кирхгофа можно сформулировать следующим образом: Алгебраическая
сумма падений напряжений U на всех элементах контура, включая источники э.д.с.,
n
равна нулю
U i 0
i 1
II правило Кирхгофа записывается только для независимых контуров.
Независимыми контурами сложной (разветвленной) цепи называются такие
контуры, которые отличаются хотя бы одним элементом цепи, не использованным
ранее в намеченных контурах.
Число независимых уравнений, составленных по II правилу Кирхгофа, равно числу
независимых контуров в цепи: f = p – (q – 1).
23

24.

Правила Кирхгофа
I правило Кирхгофа: Алгебраическая сумма токов, сходящихся в узле, равна нулю
(Сумма токов, входящих в узел, равна сумме токов, выходящих из узла)
n
Ii 0
i 1
Число уравнений, составляемых по I правилу Кирхгофа: h = q – 1
II правило Кирхгофа: Алгебраическая сумма э.д.с. в любом контуре
электрической цепи постоянного тока равна алгебраической сумме падений
напряжений на всех элементах, входящих в этот контур
n
m
i 1
k 1
Еi Rk I k
II правило Кирхгофа можно сформулировать следующим образом:
Алгебраическая сумма падений напряжений U на всех элементах контура, включая
n
источники э.д.с., равна нулю
U i 0
i 1
Число независимых уравнений, составленных по II правилу Кирхгофа, равно числу
независимых контуров в цепи: f = p – (q – 1). Независимыми контурами сложной
(разветвленной) цепи называются такие контуры, которые отличаются хотя бы одним
элементом цепи, не использованным ранее в намеченных контурах.
24

25.

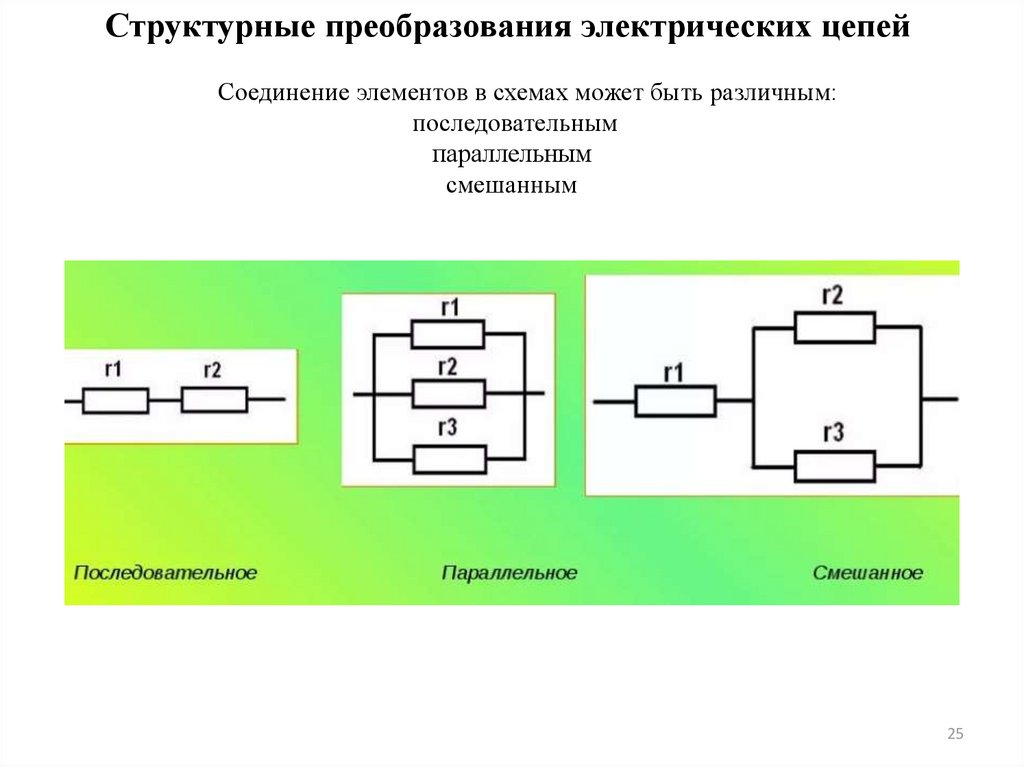
Структурные преобразования электрических цепей
Соединение элементов в схемах может быть различным:
последовательным
параллельным
смешанным
25

26.

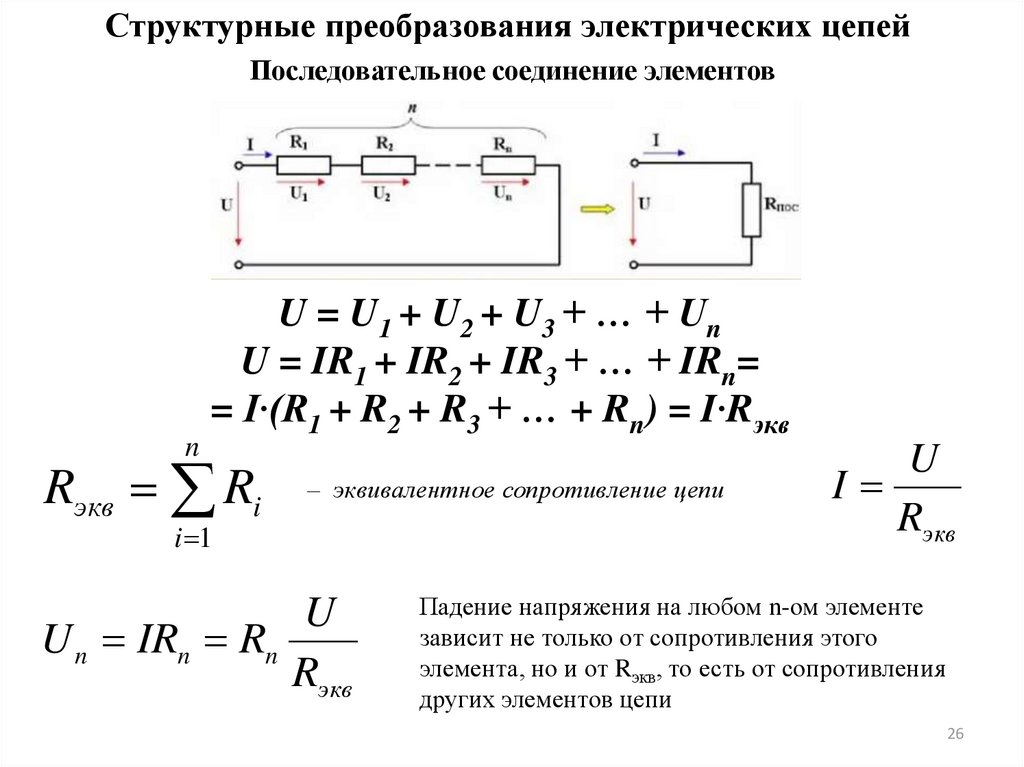
Структурные преобразования электрических цепей
Последовательное соединение элементов
n
U = U 1 + U2 + U3 + … + U n
U = IR1 + IR2 + IR3 + … + IRn=
= I∙(R1 + R2 + R3 + … + Rn) = I∙Rэкв
Rэкв Ri
– эквивалентное сопротивление цепи
i 1
U
U n IRn Rn
Rэкв
U
I
Rэкв
Падение напряжения на любом n-ом элементе
зависит не только от сопротивления этого
элемента, но и от Rэкв, то есть от сопротивления
других элементов цепи
26

27.

Структурные преобразования электрических цепей
Параллельное соединение элементов
При таком соединении ко всем элементам приложено одно и то же напряжение.
Каждый параллельно включенный элемент образует отдельную ветвь
В каждой параллельной
ветви ток
U
I n
Gn U ,
Rn
1
Gn
Rn
– проводимость
n-ой ветви
I = I1 + I2 + I3 + … + In
I = G1U + G2U + G3U + … + GnU =
U∙(G1 + G2 + G3 + … + Gn) = GэквU
n
Gэкв Gi
i 1
– эквивалентная проводимость цепи
27

28.

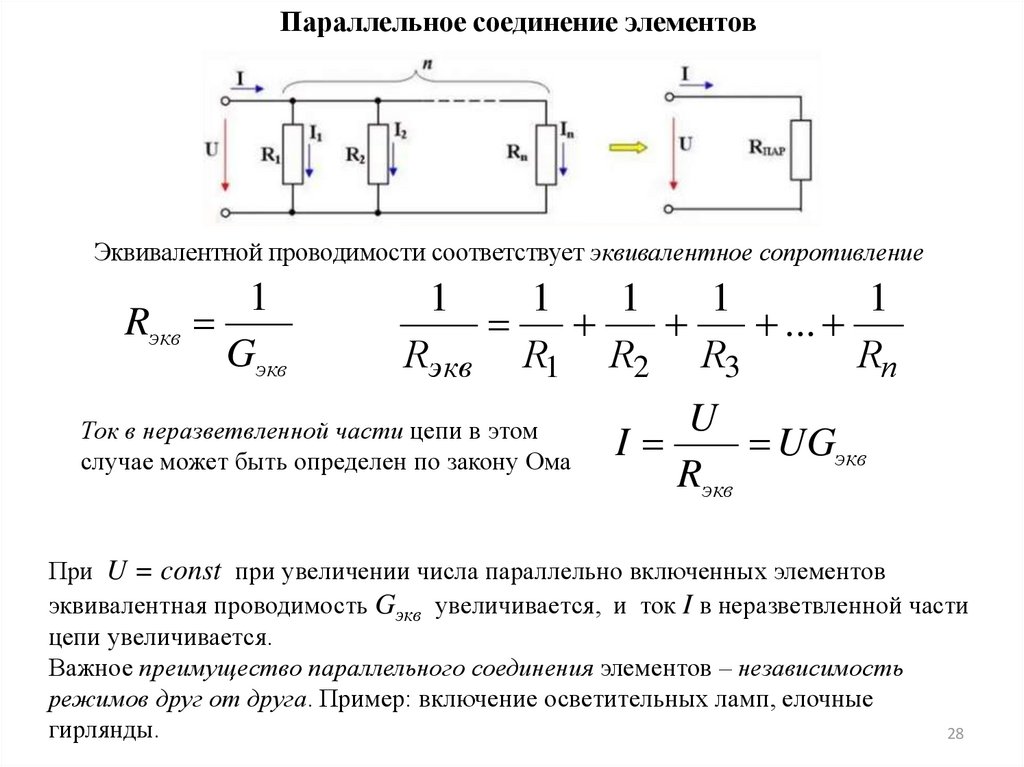
Параллельное соединение элементов
Эквивалентной проводимости соответствует эквивалентное сопротивление
Rэкв
1
Gэкв
1
Rэкв
1
1
1
1
...
R1 R2 R3
Rn
Ток в неразветвленной части цепи в этом
случае может быть определен по закону Ома
U
I
UGэкв
Rэкв
При U = const при увеличении числа параллельно включенных элементов
эквивалентная проводимость Gэкв увеличивается, и ток I в неразветвленной части
цепи увеличивается.
Важное преимущество параллельного соединения элементов – независимость
режимов друг от друга. Пример: включение осветительных ламп, елочные
гирлянды.
28

29.

Структурные преобразования электрических цепей
Смешанное соединение элементов цепи
Такое соединение представляет собой сочетание последовательного и параллельного
соединений. В этом случае цепь может иметь различное число узлов и ветвей
Для расчета такой цепи необходимо последовательно определять эквивалентные
сопротивления для тех частей схемы, которые представляют собой только
последовательное или параллельное соединение
R12 R1 R2
Ток в цепи с Rэкв:
U
I
Rэкв
R3 R4
R34
R3 R4
Это ток источника питания и ток в элементах R1 и R2
Для расчета I3 и I4 надо определить U34 :
Тогда I3 и I4 можно найти по
закону Ома для участка цепи:
Rэкв R12 R34
U 34
I3
R3
U 34 R34 I
U 34
I4
R4
29

30.

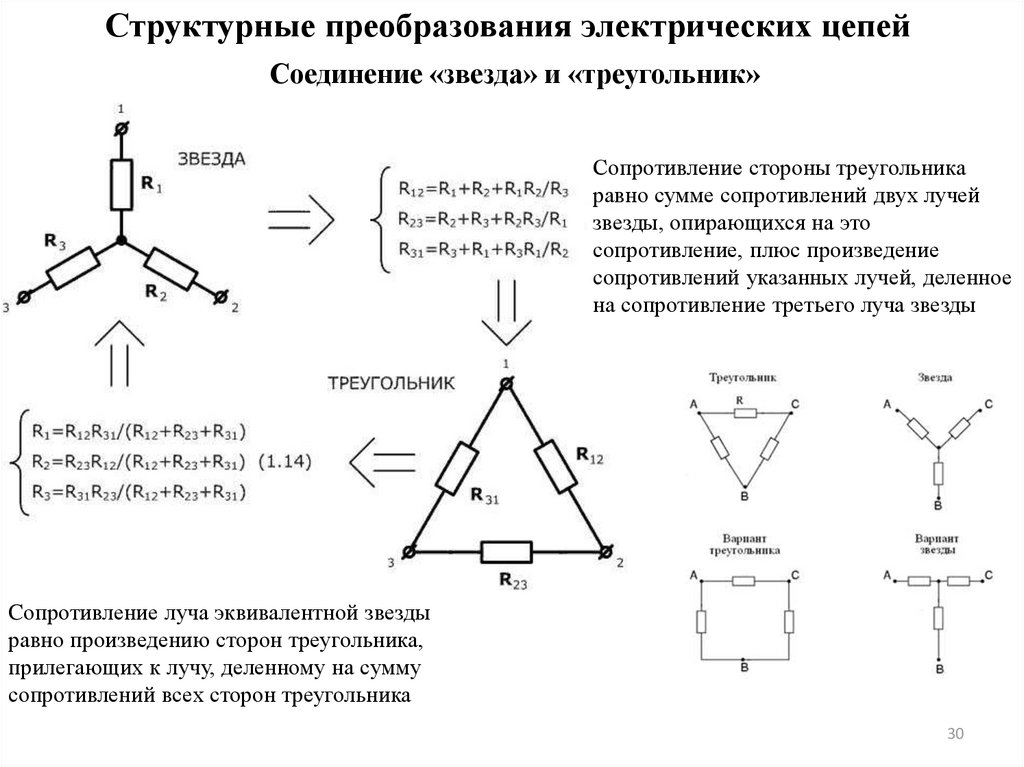
Структурные преобразования электрических цепей
Соединение «звезда» и «треугольник»
Сопротивление стороны треугольника
равно сумме сопротивлений двух лучей
звезды, опирающихся на это
сопротивление, плюс произведение
сопротивлений указанных лучей, деленное
на сопротивление третьего луча звезды
Cопротивление луча эквивалентной звезды
равно произведению сторон треугольника,
прилегающих к лучу, деленному на сумму
сопротивлений всех сторон треугольника
30

31.

Методы расчета электрических цепей
Метод узловых и контурных уравнений
31

32.

32

33.

Мощность
Работа, которую совершает источник для перемещения заряда q по всей замкнутой цепи:
Wист = q∙E,
где q = I∙t, E = U + Uвт,
Wист = (U + Uвт)∙I∙t = U∙I∙t + Uвт ∙I∙t,
где W = U∙I∙t – работа, совершаемая источником на внешнем участке цепи,
Wвт = Uвт ∙I∙t – потери энергии внутри источника
W I 2 Rt
В соответствии с законом Ома для участка цепи
Мощность − это работа, совершаемая в единицу времени
Мощность, отдаваемая источником
E I t
Pист
E I
t
W
P
t
Мощность потребителей
2
U I t
U
P
U I I 2R
t
R
Мощность потерь энергии внутри источника
2
U
Рвт U вт I I 2 Rвт вт
Rвт
Единица измерения мощности – ватт [Вт], [кВт], [МВт]
33

34.

Баланс мощностей
Баланс мощностей − следствие закона сохранения энергии:
суммарная мощность, вырабатываемая источниками,
равна сумме мощностей, потребляемых в цепи
EI RI
2
Баланс мощностей составляется обычно для проверки правильности
решения задач
34

35.

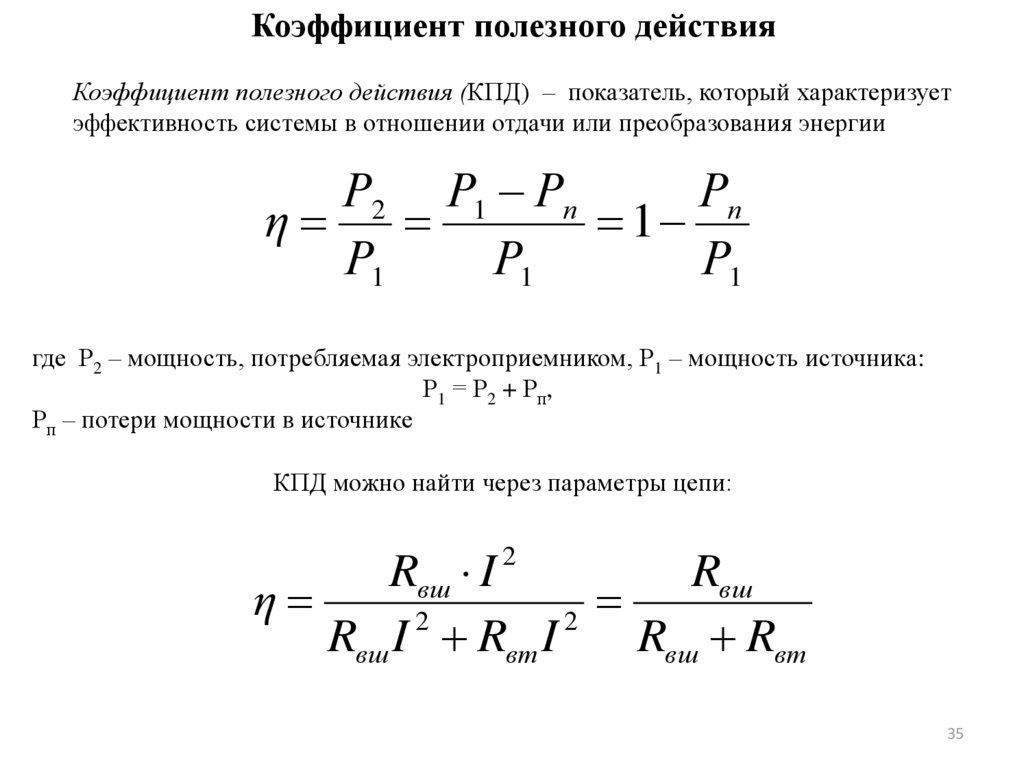
Коэффициент полезного действия
Коэффициент полезного действия (КПД) – показатель, который характеризует
эффективность системы в отношении отдачи или преобразования энергии
Р2 Р1 Рп
Рп
η
1
Р1
Р1
Р1
где Р2 – мощность, потребляемая электроприемником, Р1 – мощность источника:
Р1 = Р2 + Рп,
Рп – потери мощности в источнике
КПД можно найти через параметры цепи:
Rвш I 2
Rвш
η
2
2
Rвш I Rвт I
Rвш Rвт
35

36.

Режимы работы электрической цепи
Режим работы
Условие
хх
Rвш = ∞
ном
Uном, Pном
с
Rвш = Rвт
кз
Rвш = 0
Ток
I хх
E
0
Rвт Rвш
Iном
E
0,5 I кз
2 Rвт
E
Е
I кз
max
Rвт Rвш Rвт
I
КПД
η=1
η = ηном
η = 0,5
η=0
36

37.

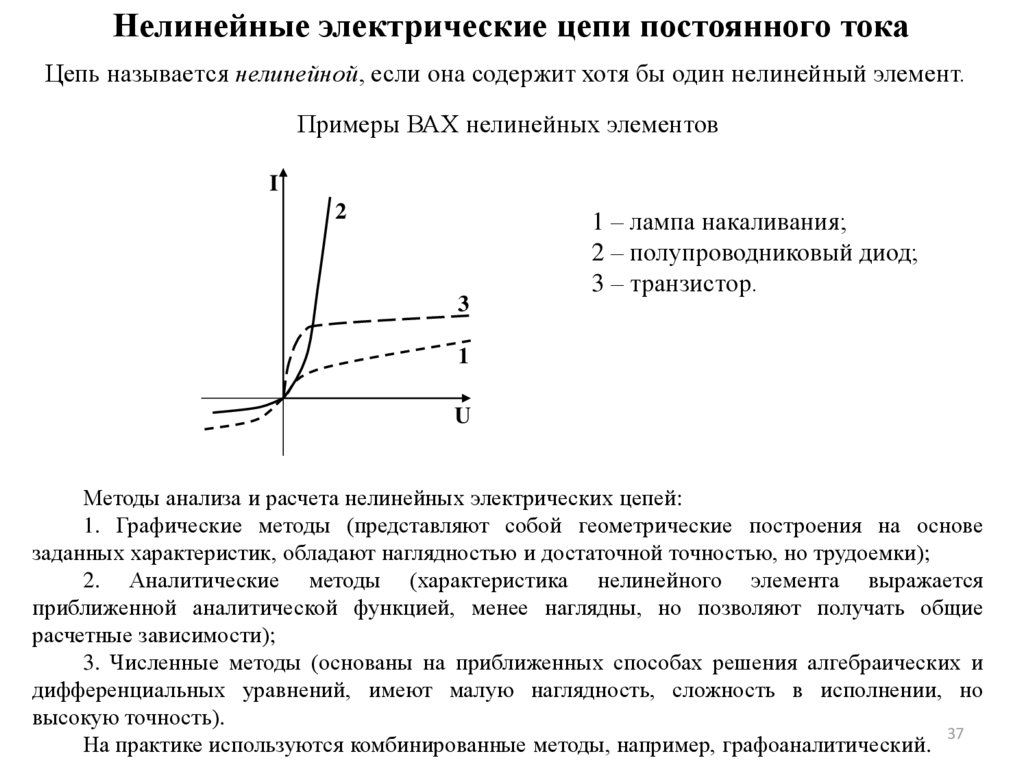
Нелинейные электрические цепи постоянного тока
Цепь называется нелинейной, если она содержит хотя бы один нелинейный элемент.
Примеры ВАХ нелинейных элементов
I
2
3
1 – лампа накаливания;
2 – полупроводниковый диод;
3 – транзистор.
1
U
Методы анализа и расчета нелинейных электрических цепей:
1. Графические методы (представляют собой геометрические построения на основе
заданных характеристик, обладают наглядностью и достаточной точностью, но трудоемки);
2. Аналитические методы (характеристика нелинейного элемента выражается
приближенной аналитической функцией, менее наглядны, но позволяют получать общие
расчетные зависимости);
3. Численные методы (основаны на приближенных способах решения алгебраических и
дифференциальных уравнений, имеют малую наглядность, сложность в исполнении, но
высокую точность).
37
На практике используются комбинированные методы, например, графоаналитический.

38.

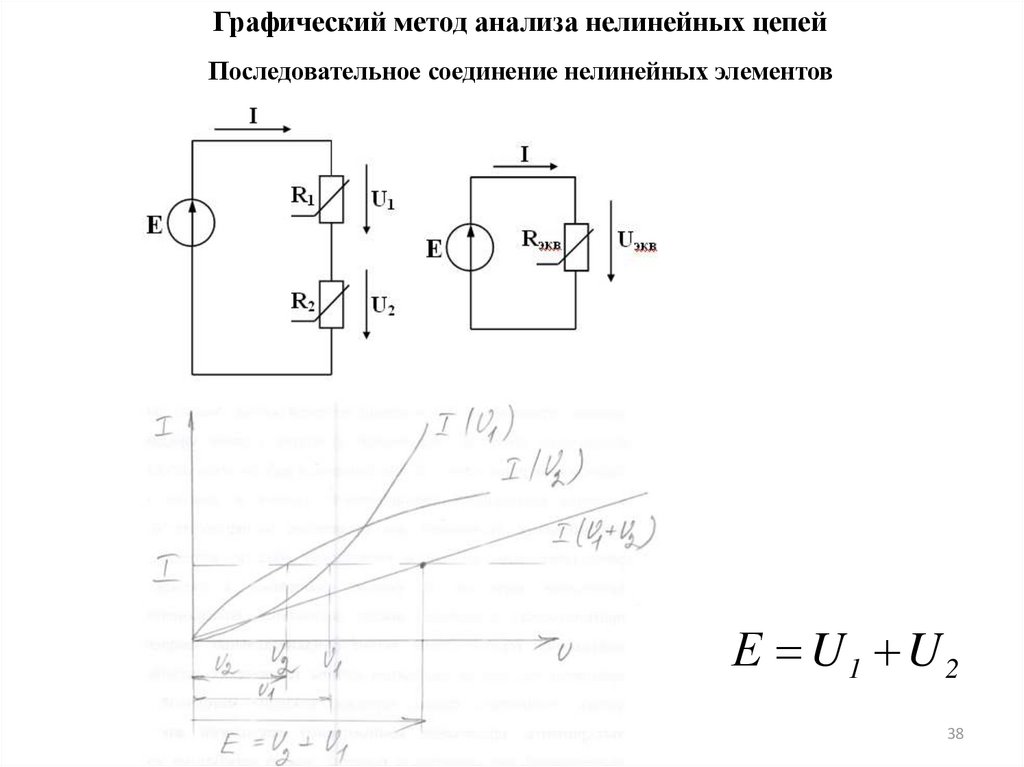
Графический метод анализа нелинейных цепей
Последовательное соединение нелинейных элементов
Е U1 U 2
38

39.

Графический метод анализа нелинейных цепей
Параллельное соединение нелинейных элементов
39