Көрсеткіштік және логарифмдік теңдеулерді шешу әдістері

1. КӨРСЕТКІШТІК ЖӘНЕ ЛОГАРИФМДІК ТЕҢДЕУЛЕРДІ ШЕШУ ӘДІСТЕРІ

2. Мазмұны

МАЗМҰНЫ
Кіріспе......................................................................................................
1 Көрсеткіштік және логарифмдік теңдеулерді шешудің
теориялық негіздері...............................................................................
1.1 Көрсеткіштік және логарифмдік
функциялар....................................
2 Көрсеткіштік және логарифмдік теңдеулерді шешу
әдістері...............
2.1 Көрсеткіштік және логарифмдік
теңдеулердің түрлері.........................................................................
2.2 Мектеп математика курсында көрсеткіштік және
логарифмдік теңдеулерді шешу...........................................................
Қорытынды............................................................................................
Пайдаланылған әдебиеттер тізімі.........................................................

3. Кіріспе

КІРІСПЕ
Ғылыми мәселенің қазіргі кездегі шешу жағдайын бағалау. Жалпы білім
беретін орта мектепте математиканы оқытудың негізгі міндеті - қазіргі
қоғамның әрбір мүшесінің күнделікті тіршілік тынысы мен еңбек әрекетіне
қажетті салалас пәндерді оқып үйренуге және білімін одан әрі жалғастыруға
жеткілікті математикалық білім мен икемділікті оқушылардың жүйелі түрде
тиянақты әрі саналы меңгеруін қамтамасыз ету.
Жұмыстың өзектілігі. Осы 11-сыныпта оқытылатын «Алгебра және анализ
бастамалары» курсын үлкен бес тарауға бөлуге болады. Біріншісін алғашқы
функция тарауына және кейінгісін дәреже және түбір,дәрежелік функция,онан
соң көрсеткіштік және логарифмдік функциялар тарауына бөледі.
Жүргізген зерттеудің мақсаты - осы курстың үшінші тарауындағы
көрсеткіштік және логарифмдік теңдеулерін функция қасиеттеріне сүйене
шешуге арналған. Осы көрсеткіштік, логаримфдік функция тарауының негізгі
мақсаты - окушылардың көрсеткіштік, логарифмдік функциялармен және
олардың қасиеттерімен таныстыру (е саны және натурал логарифмдер туралы
мағлұматтар да енеді); күрделі көрсеткіштік және логарифмдік теңдеулерді,
олардың жүйелерін (иррационал теңдеулер енетіндерін де) шешуге үйрету.

4.

Зерттеу нысаны-логарифмдік және көрсеткіштік теңдеулерді шығарту
процесі.
Зерттеу жұмысының әдістемелік негіздері-педагогикалық және
әдістемелік әдебиеттерден тақырыпқа сай материалдар жинақтап,озат
мұғалімдердің сабақтарына қатысу,бақылау,ізденушілік және
зерттеушілік жұмыстары.
Зерттеу мақсаты-оқушылардың дәреже туралы мағлұматтарын
жүйеге келтіру және қорытындылау, күрделі көрсеткіштік және
логаримдік теңдеулерді шешуге үйрету.
Зерттеу міндеті-логарифмдік және көрсеткіштік теңдеулерді есептерді
шешудің түрлері және оны оқытуда пайдалану.
Жұмыстың жаңалығы: көрсеткіштік және логарифмдік теңдеулерді
шешудің әдістері мен тәсілдері анықталды
Жұмыстың практикалық құндылығы-логарифмдік және
көрсеткіштік теңдеулерге берілген есептерді шығару арқылы
оқушылардың математикалық деңгейі және пәнге деген
қызығушылығының нәтижесі қалыптасады
Дипломдық жұмыстың құрылымы: Дипломдық жұмыс кіріспе,
екі бөлім, қорытынды, пайдаланылған әдебиеттер тізімінен тұрады.

5. 1.КӨРСЕТКІШТІК ЖӘНЕ ЛОГАРИФМДІК ТЕҢДЕУЛЕРДІ ШЕШУДІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ 1.1 Көрсеткіштік және логарифмдік функциялар

1.КӨРСЕТКІШТІК ЖӘНЕ ЛОГАРИФМДІК ТЕҢДЕУЛЕРДІ
ШЕШУДІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ
1.1 КӨРСЕТКІШТІК ЖӘНЕ ЛОГАРИФМДІК ФУНКЦИЯЛАР
Көрсеткіштік функция
у=ах (а >0, а^І) түріндегі функцияны
көрсеткіштік функция деп атаймыз. Осы
функцияны зерттейік.
1) у=ах функциясының анықталу облысы
бүкіл абцисса өсін қамтиды, яғни бүкіл сан
түзуі болады.
2) у=ах функциясы тақ та емес; жұп та емес.
3) у=ах функциясы аргументтің барлық
мәндерінде оң болғандықтан, оның графигі
абцисса өсінен жоғары орналасады.
Егер а>1, онда х>0 болғанда ах >1 болады
және х<0 болған жағдайда ах<1 болады.
Басқа кез келген жағдайында ах|х=0=1.
Графигі Оу өсі арқылы (0,1) нүктесінен
өтеді.
4) Егер а>1, онда у=ах функциясы
бірсарынды өседі; егер а<1 болса, онда ол
бірсарынды кемиді.

6. Логарифмдік функция

ЛОГАРИФМДІК ФУНКЦИЯ
Логарифмдік функция
Мына түрдегі
функциясын логаримфмдік функця деп атайды, мұндағы а>0
және а≠1.
Логарифмдік функция графигін салмас бұрын,
оның көрсеткіштік функцияға кері функция екенін
байқаймыз. Шынында да егер
және у=ах
өзара кері функциялар болып табылады. Олардың
графиектері І-ІІІ координатық бұрыштардың
биссектрисасына қарағанда симметриялы
орналасады[4].
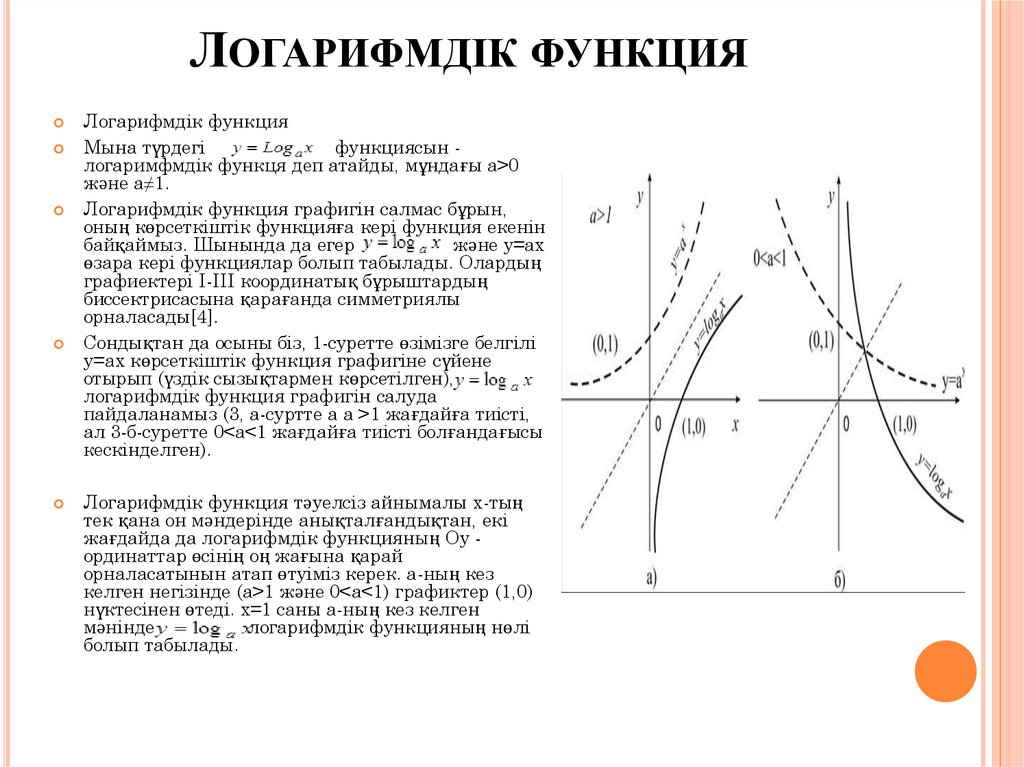
Сондықтан да осыны біз, 1-суретте өзімізге белгілі
у=ах көрсеткіштік функция графигіне сүйене
отырып (үздік сызықтармен көрсетілген),
логарифмдік функция графигін салуда
пайдаланамыз (3, а-суртте а а >1 жағдайға тиісті,
ал 3-б-суретте 0<а<1 жағдайға тиісті болғандағысы
кескінделген).
Логарифмдік функция тәуелсіз айнымалы х-тың
тек қана он мәндерінде анықталғандықтан, екі
жағдайда да логарифмдік функцияның Оу ординаттар өсінің оң жағына қарай
орналасатынын атап өтуіміз керек. а-ның кез
келген негізінде (а>1 және 0<а<1) графиктер (1,0)
нүктесінен өтеді. х=1 саны а-ның кез келген
мәнінде
логарифмдік функцияның нөлі
болып табылады.

7. 2 КӨРСЕТКІШТІК ЖӘНЕ ЛОГАРИФМДІК ТЕҢДЕУЛЕРДІ ШЕШУ ӘДІСТЕРІ 2.1 Көрсеткіштік және логарифмдік теңдеулердің түрлері

2 КӨРСЕТКІШТІК ЖӘНЕ ЛОГАРИФМДІК ТЕҢДЕУЛЕРДІ
ШЕШУ ӘДІСТЕРІ
2.1 КӨРСЕТКІШТІК ЖӘНЕ ЛОГАРИФМДІК ТЕҢДЕУЛЕРДІҢ ТҮРЛЕРІ
Көрсеткіштік теңдеулер
Алдыңғы
тарауда
біз
мектеп
математика
курсындағы
көрсеткіштік
теңдеулерді типтерге бөліп, олардың әрқайсысына тоқталып өткен едік. Енді
болса көрсеткіштік теңдеулердің барлық жалпы түрлерін көрсетіп, олардың
шешуі жолдарын көрсетуді мақсат тұттық[11].
1. Қарапайым көрсеткіштік теңдеу мына түрде беріледі:
a x b a 0, a 1
Егер b > о болса, теңдеудің түбірі жоқ болады.
Мысалдар
1
3 теңдеуін шешейік.
1) 7 5 x
Шешуі: Екі жағынан да 7 негізі бойынша логарифм аламыз.
5 x 1 log 7 7 log 7 3 5 x 1 log 7 3 5 x log 7 3 1
log 7 3 1
Жауабы:
x
5
2) 3 x 3 5 x 7 x 12
Шешуі: Екі жағынан да 3 негізі бойынша логарифм алып, берілген
теңдеуге мәндес теңдеуге көшсек: x 3 x 2 7 x 12 log 3 5 . Бұл теңдеуді
квадраттық теңдеу ретінде шешуге болады, бірақ коэффициенттері қолайсыз.
Сондықтан да теңдеуді әрі қарай түрлендіреміз:
x 3 x 3 x 4 log 3 5; x 3 x 3 x 4 log 3 5; x 3 1 x 4 log 3 5 0
x1 3
x 3 0
1 x 4 log 3 5 0
1 x log 3 5 4 log 3 5 0
1 4 log 3 5 log 5 3 4;
2
Жауабы: x1 3,
f
x2 4 log 5 3
x 1
түріндегі теңдеулер
a
2.
Мысалдар
1)
2x
2
5 x 6
1
x 2 5 x 6
Шешуі:
2
20
болады, x1 2 және x2 3
Негіздері тең болғандықтан,
x 2 5 x 6 0;
берілген теңдеудің түбірлері болады.
8s in x cos x 0,5 =1
2)
Шешуі: Мәндес теңдеуге көшсек:
2
2x
2 k , k Z , x
k , k Z
3
3
2
тең
2
cos2 x sin 2 x 0,5 0,
cos 2 x 0,5,

8.

2.2 Мектеп математика курсындағы көрсеткіштік және
логарифмдік теңдеулерді шешу
Мектеп
курсында
көрсеткіштік
теңдеулерді
шешу
көрсеткіштік
функцияның негізгі қасиеттеріне сүйене отырып шешіледі. Енді осы есептердің
бірнешеуінің шығару жолдарын келтіре кетейік[26].
1-есеп. Теңдеуді шеш. а) 3 x 1 2 3 x 2 75,
1
Бұл теңдеуді мына түрде жазып: 3 x 3 2 3 x 2 75, және 3х-ті жақша
3
сыртына шығарсақ,
2
25
3 x 3 75, 3 x
75, 3 x 27, 3 x 33 , x 3
9
9
Теңдеуді табылған түбірін теңдеуге қойсақ, дұрыстығына көз жеткіземіз.
1
б)
5
x 1
1
5
x
x 1
4,8 . Берілген теңдеуді түрлендіріп мына түрде жаза
x
x
1
48
1
24
1
1
1
1
, 5
аламыз 5
5
10
5
5
5
5
5
5
1
Соңғы теңдіктен
5
x
24
24
5
5
x
1 аламыз, сөйтіп, х=0 түбірі табылады.
1
1
1
24
24
1
4,8, 5
4,8,
Тексеру:
5
5
5
5
5
x 2
x 2
3
2-есеп а) 2
теңдеуін шешу керек. Бұндай түрдегі көрсеткіштік
теңдеулерді 3-тип-негіздері әр түрлі, бірақ дәреже көрсеткіштері бірдей болып
келетін теңдеулерге жатқызамыз.
Шешуі: Теңдеудің екі жағын да 3 x 2 0 өрнегіне бөліп жіберсек:
x 2
2x 2
2
1
x 2
3
3
Тексеру.
22 2
қанағаттандырады.
Жауабы: х=2
0
2
, x 2 0, x 2 түбірін аламыз.
3
табылған
32 2 20 30 ,1 1
түбір
теңдеуді

9. ҚОРЫТЫНДЫ

Жалпы білім беретін орта мектептің 11-сыныбындағы «Көрсеткіштік және логарифмдік
теңдеулерді шешудің әдістері» тақырыбын оқып-үйренуде ескерілетін нәрсе:
1. Теорияның негізгі ережелерін білу (Логарифмдік және көрсеткіштік тепе-теңдік,
логарифмдік теңдіктерді көрсеткіш түрінде және көрсеткіштік теңдіктерді логарифмдік
түрде жазу, негізгі теоремалар мен анықтамаларды меңгеру);
2. Көрсеткіштер мен логарифмдер теориясын есептер шығару тәжірибесінде қолдана
білу (тепе-тең түрлендірулерді орындау, көрсеткіштік және логарифмдік теңдеулерді
шешу);
3. Алгебралық теңдеулер мен теңсіздіктердің теориясы мен шешу амалдарын
«көрсеткіштер», «логарифмдер» тақырыбына байланысты жаңа жағдайға көшіру, есеп
шығару үстінде білімді жүйелеу:
Жұмыстың негізгі арқауы болған «Көрсеткіштік және логарифмдік теңдеулер»
тақырыбындағы білімнің жоғарыда келтірген түрлеріне кеңірек тоқталып, теңдеулерді
шешу амалдарын және білімді жүйелеу мақсатында оны оқып үйренуде кездесетін
қиындықтарды жою жолдарын қарастырдым.
Мектеп оқулықтарындағы осы тақырыптарға арналған есептеріне талдау жасалынып,
олардың шығарылу жолдары көрсетілді
Жалпы, қорыта айтар болсақ, біздің осы бітіруші жұмысымыздың дидактикалық
мақсаты - көрсеткіштік, логарифмдік функциялар туралы мағлұматтарды бір жүйеге
келтіріп, жинақтап қорыту және осы функциялардың қасиеттерін есептер шығаруға
қолдану іскерліктерін қалыптастыру болып табылады.
Осы тақырыпта қарастырылған мәселелер, есептер, талдаулар мұғалімнің практикалық
жұмысына үлкен септігін тигізеді деген сенім білдіремін.

10. ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

1 Әбілқасымова А.Е. Жалпы білім беретін мектептің жаратылыстану –
математика бағытындағы 11-сыныбына арналған оқулық-Алматы:Мектеп
баспасы,2007.-213б.
2 Бияров Т.Н., Молдабеков М.М. Элементар математика есептерінің жинағы.
Алматы. 1992.-187б.
3 Айдос Е.Ж., Балықбаев Т.О. Математика пәні бойынша жоғары оқу
орындарына түсушілерге арналған оқу құралы. Алматы. 2006.-254б.
4 Под редакцией М.Н.Сканави. Сборник задач по математике срешениями.
Москва. «Алъянс-В». 1999.-321с.
5 Антонов Н.П., Выгодский М.Я., Никитин В.В., Санкин А.И. «Сборник задач по
элементарной математике». Пособие для самообразования. Москва, 1961.-254с.
6 Рустюмова И.П., Рустюмова С.Т. Пособие для подготовки к единому
национальному тестированию по математике Алматы,2011.-247с.
7 Колмогоров А.Н.және т.б. «Алгебра және анализ бастамалары». Орта мектептің
10-11 сыныптарына арналған оқулық. Алматы. «Рауан». 1996.-236б.
8 Болтянский Г., Сидоров Ю.В., Шабунин М.И. «Лекции и задачи по
элементарной математике». Москва. «Наука». 1974.-231с.
9 Колмогоров А.Н.және т.б. «Алгебра және анализ бастамалары». Орта мектептің
9-10 сыныптарына арналған оқу құралы. Алматы. «Мектеп». 1988.-236б.
10 Зорин В.В. Пособие по математике для поступающих в ВУЗы. Москва.
«Высшая школа» 1973.-198с.