Явление электромагнитной индукции. Теория Максвелла для электромагнитного поля. Лекция № 16

1.

Лекция № 16
Явление электромагнитной
индукции. Теория Максвелла
для электромагнитного поля
А. А. Детлаф, Б. М. Яворский,
25.1 – 25.3; 26.1 – 26.5
Н.П.Калашников, Н.М. Кожевников.
Интернет-тестирование базовых
знаний, 3 ДЕ

2.

Литература по теме
«Явление электромагнитной
индукции. Теория Максвелла для
электромагнитного поля»
Т. И. Трофимова, §§122 – 130,
137 – 139;
А. А. Детлаф. Б. М. Яворский.
25.1 – 25.6; 26.1 – 26.5;
Н. П. Калашников,
Н. М. Кожевников,
3 ДЕ, задания 14 - 16.

3.

Майкл Фарадей
1791 – 1867гг.
Области научных
интересов:
электричество,
магнетизм,
магнитооптика,
электрохимия

4.

1831 г.
Открыто М.Фарадеем:
в замкнутом проводнике под
действием магнитного поля
возникает электрический ток.

5.

Открытая физика

6.

Индукционный ток возникает при
изменении магнитного потока,
пронизывающего поверхность,
натянутую на контур.

7.

dS
dФ B BdS BdSCos ;
dS n dS ;
B
n
При
( n B );
ФB BdS BdSCos .
В const и cos const
ФВ BS cos . ФВ Тл м Вб
2

8.

- теорема Гаусса для
B
d
S
0
S
МП.
Число силовых линий для
замкнутой поверхности равно
нулю, соленоидальное МП
создается движущимся
электрическим зарядом .

9.

i
dФB
i
dt
- ЭДС электромагнитной
индукции;
dФB
- скорость изменения
dt магнитного потока;
« - » учитывает правило Ленца.

10.

(выражает закон сохранения энергии)
-ИНДУКЦИОННЫЙ ТОК ИМЕЕТ ТАКОЕ
НАПРАВЛЕНИЕ, ЧТО ЕГО МАГНИТНОЕ ПОЛЕ ПРОТИВОДЕЙСТВУЕТ
ИЗМЕНЕНИЮ МАГНИТНОГО ПОТОКА.

11.

Индукция магнитного поля
увеличивается,
Ф 0

12.

Среднее значение ЭДС индукции
<
ФB
>
i t .
Магнитный поток изменяется при:
а) изменении В;
б) изменении формы контура;
в) изменении положения контура
в магнитном поле.

13.

Открытая физика

14.

15.

и в отрезке проводника,
пересекающем при своём
движении линии магнитной
индукции поля.

16.

B const
Проводник
длиной
движется
горизонтально
в однородном
магнитном
поле ( В )

17.

Джеймс Клерк Максвелл
( 1831 – 1879 )

18.

Феноменологическая
теория
электромагнитного поля.
Содержит восемь основных
(4 в интегральной и 4 в
дифференциальной форме
записи) и три дополнительных уравнения.

19.

1860—1865 Максвелл создал
теорию электромагнитного поля,
которую сформулировал в виде
системы уравнений.
Любые изменения электрического
и магнитного полей – волны, распространяющиеся в среде.
Их скорость зависит от и . .

20.

D
d
S
Q
;
своб
S
BdS 0.
S
В ИНТЕГРАЛЬНОЙ ФОРМЕ
СПРАВЕДЛИВЫ ДЛЯ НЕПОДВИЖНЫХ ЗАМКНУТЫХ КОНТУРОВ И
ПОВЕРХНОСТЕЙ, МЫСЛЕННО
ПРОВЕДЕННЫХ
В
ЭМ
ПОЛЕ.
B
H
d
I
I
;
E
d
d
S
;
макро
см
t
L
S
L

21.

Система уравнений
Максвелла в интегральной
форме записи:
B
D
d
S
Q
;
E
d
d
S
;
своб
t S
L
S
B
d
S
0
.
H
d
I
I
;
макро
см
L
S

22.

B
E
d
d
S
t
L
S
Циркуляция вектора E вдоль
произвольного замкнутого контура
L равна взятой с обратным знаком
скорости изменения магнитного
потока через поверхность S ,
натянутую на этот контур.

23.

Закон электромагнитной индукции в трактовке Дж.Максвелла

24.

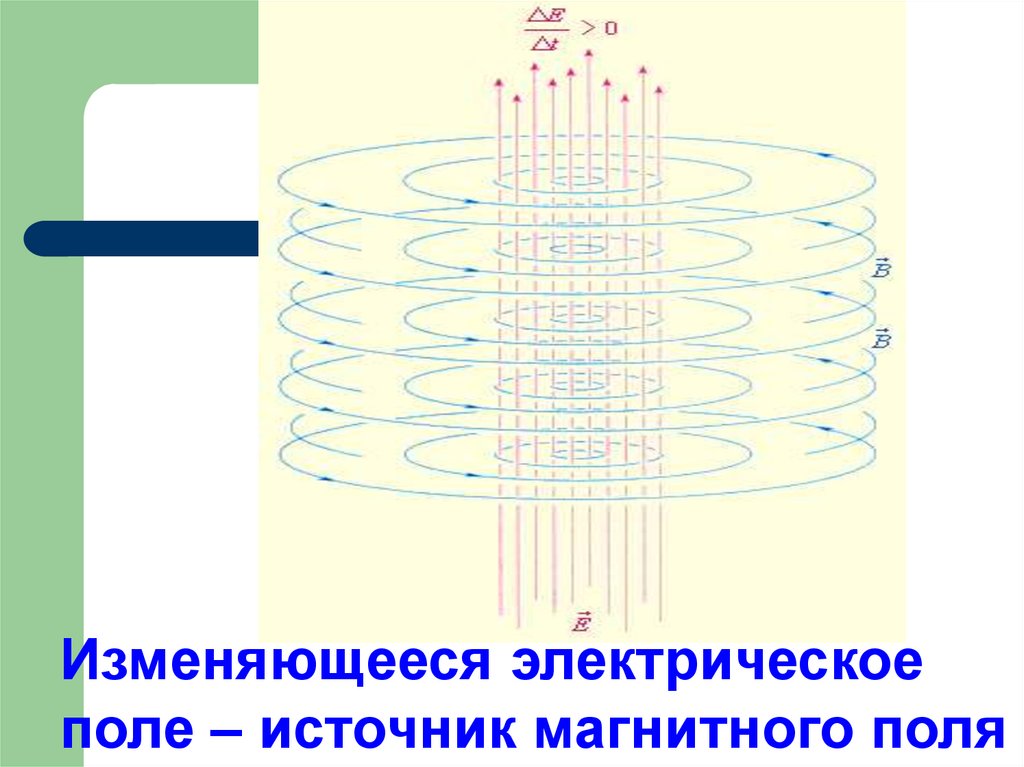
магнитное поле создаИдея: ется не только движущимся электрическим
зарядом.
Источник переменного магнитного поля - переменное электрическое поле.
Количественной характеристикой «магнитного действия»
переменного электрического
поля служит ток смещения I cм .

25.

Изменяющееся электрическое
поле – источник магнитного поля

26.

I cм
j dS
S
– ИСТОЧНИК ВИХРЕВОГО МАГНИТ-
НОГО
ПОЛЯ.
j - ПЛОТНОСТЬ ТОКА СМЕЩЕНИЯ,
jсм
jсм
E P
0
.
t t
ТОК СМЕЩЕНИЯ НЕ СОПРОВОЖДАЕТСЯ ВЫДЕЛЕНИЕМ ТЕПЛОТЫ.

27.

Обобщение закона полного тока в
среде
Hd I макро I см
Циркуляция вектора H вдоль
L
произвольного замкнутого
контура L равна алгебраической сумме макротоков и тока
смещения сквозь поверхность
S , натянутую на этот контур.

28.

D
d
S
Q
своб
S
Теорема Гаусса справедлива и
для переменного
электрического поля: поток
смещения через произвольную
замкнутую поверхность равен
суммарному свободному
заряду, находящемуся внутри
этой поверхности.

29.

Свидетельствует об отсутствии
магнитных зарядов.
B
d
S
0
- поток вектора B сквозь
S
произвольную замкнутую
поверхность равен нулю.
Магнитное поле всегда
соленоидально.

30.

Характеризуют
электрические
и магнитные
свойства
среды:
D 0 E; B 0 H .
Для изотропных однородных
сред и макротоков, подчиняю
щихся закону Ома: j E.

31.

Для стационарных полей:
E const; H const;
E
d
0
;
H
d
I
;
L
D
d
S
Q
;
S
L
B
d
S
0
.
S

32.

B - обобщение закона
E
d
d
S
L
S t ЭМ индукции, пере менное ЭМ поле;
D
- закон полного
H
d
j
d
S
L
S t тока для поля в
среде;
D
d
S
dV
- наличие заряжен
S
V
B
d
S
0
S
ных тел;
- отсутствие магнитных
зарядов.

33.

Cистема уравнений справедлива
для переменного
ЭМ поля
B
L Ed S t dS ;
D
H
d
j
L
S t dS ;
DdS dV ;
B
E
d
d
S
;
L
S t
D
L Hd S dt dS ;
DdS 0;
BdS 0
B
d
S
0
S
S
V
S
S
в отсутствие заряженных тел и
токов проводимости

34.

Cистема уравнений (2) справедлива
для стационарного
ЭМ
поля
B (1)
Ed 0;
(2)
E
d
d
S
;
L
S t
L
D
D
Hd
dS ;
H
d
j
L
S t dS ; L S dt
D
d
S
0
;
S
D
d
S
dV
;
S
V
BdS 0
0
S
S BвdSотсутствие
токов проводимости и
заряженных тел.

35.

Первое уравнение Максвелла –
обобщение…
B
1. Ed dS ;
L
S t
D
dS ;
2. Hd j
t
L
S
3. DdS dV ;
S
V
4. BdS 0
S
закона
электромагнитной
индукции

36.

Второе уравнение Максвелла сформулировано на основе обобщения…
B
1. Ed
L
S t dS ;
D
2.
H
d
j
L
S t dS ;
3.
DdS dV ; закона
S
4.
V
BdS 0
S
полного тока
в среде

37.

Физический смысл уравнения (4)
свидетельствует о
том, что…
B
1. Ed dS ;
L
S t
D
dS ;
2. Hd j
t
L
S
3. DdS dV ;
S
V
4. BdS 0
S
магнитные
заряды
отсутствуют