Уравнения Максвелла для электромагнитного поля

1. Уравнения Максвелла для электромагнитного поля

ВоГУ
Лекция 31 (13)
Уравнения Максвелла для
электромагнитного поля
Кузина Л.А.,
к.ф.-м.н., доцент
2017 г.
1

2. План

2

3.

Теория Максвелла для электромагнитного поля
Теория Максвелла для электромагнитного поля –
это обобщение :
•теоремы Остроградского-Гаусса
•закона полного тока
•закона электромагнитной индукции Фарадея
Теория решает задачу электродинамики:
найти характеристики электрического и магнитного
полей системы зарядов и токов
3

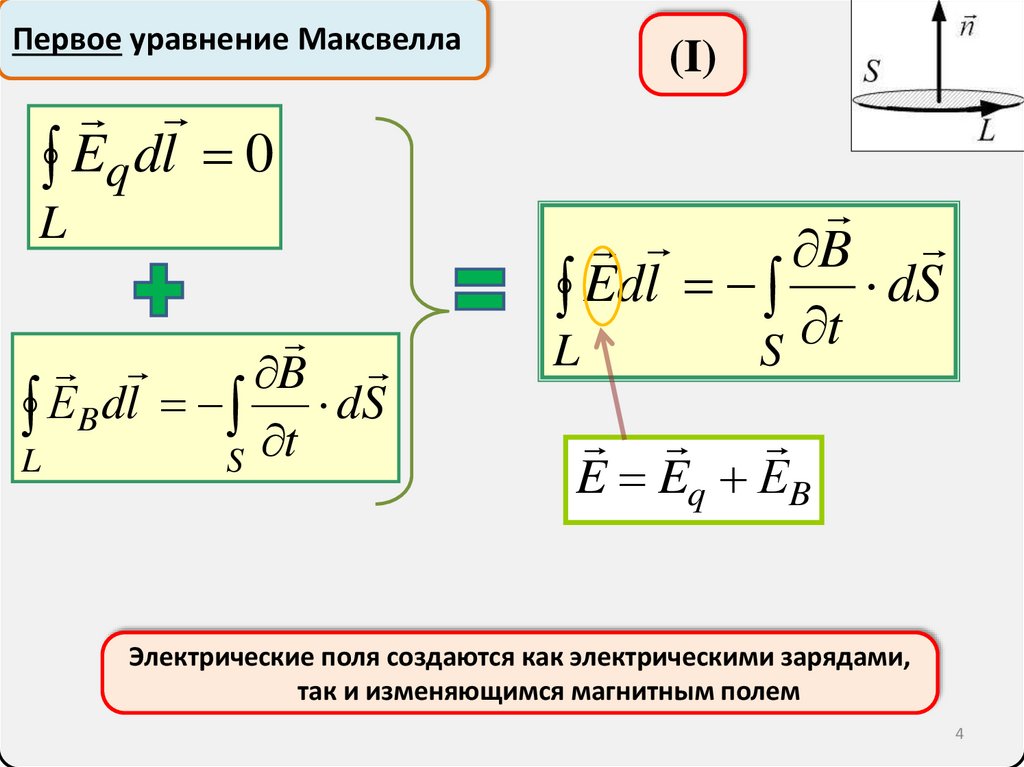
4.

Первое уравнение Максвелла
Eq dl 0
L
B
ЕB dl t dS
L
S
(I)
B
Edl t dS
L
S
E Eq ЕB
Электрические поля создаются как электрическими зарядами,
так и изменяющимся магнитным полем
4

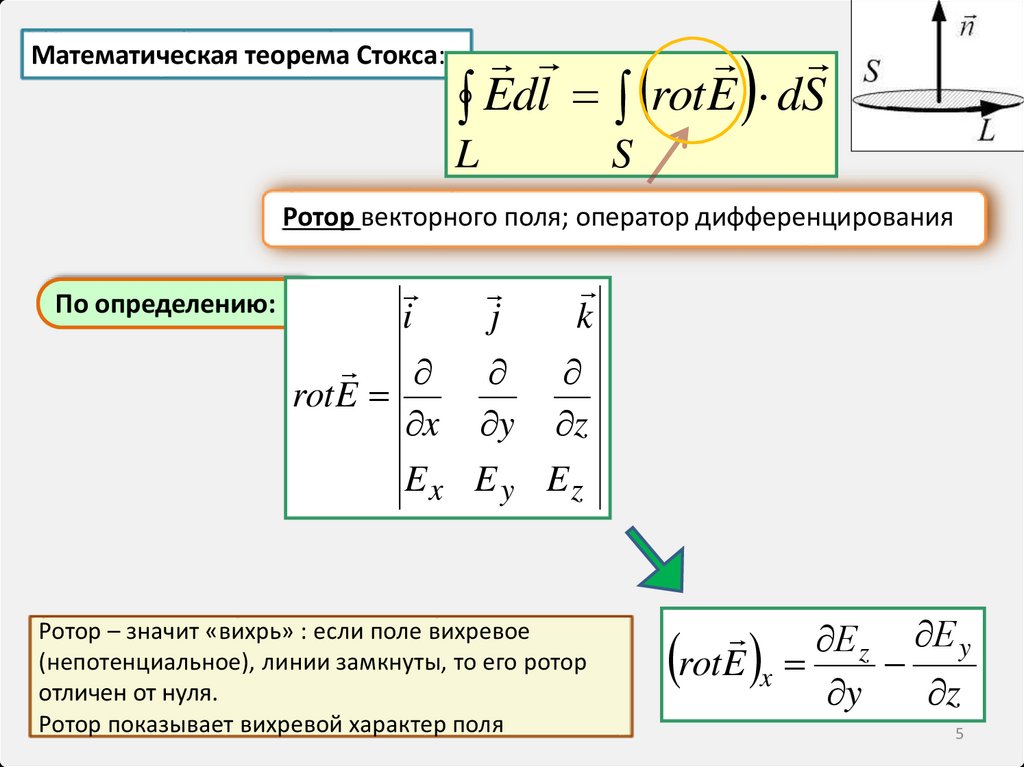
5.

Математическая теорема Стокса:
Edl rotE dS
L
S
Ротор векторного поля; оператор дифференцирования
По определению:
i
j
k
rot E
x y z
Ex E y Ez
Ротор – значит «вихрь» : если поле вихревое
(непотенциальное), линии замкнуты, то его ротор
отличен от нуля.
Ротор показывает вихревой характер поля
rot E
x
Е z Е y
y
z
5

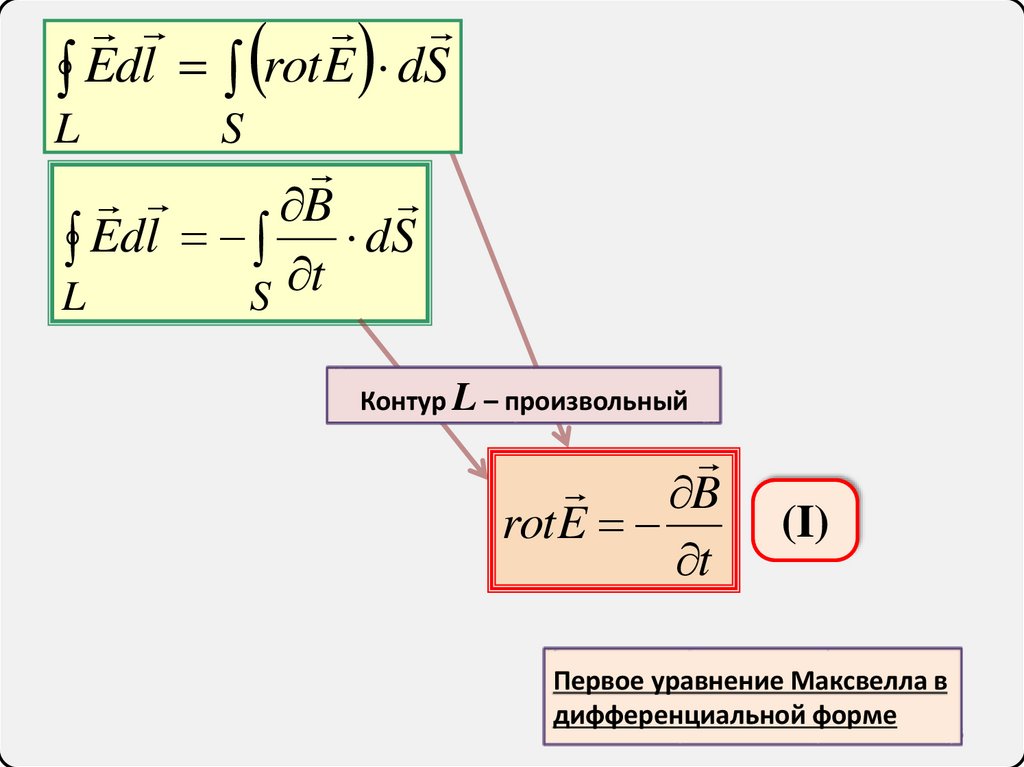
6.

Edl rotE dS
L
S
B
Edl t dS
L
S
Контур L – произвольный
B
rotE
t
(I)
Первое уравнение Максвелла в
дифференциальной форме
6

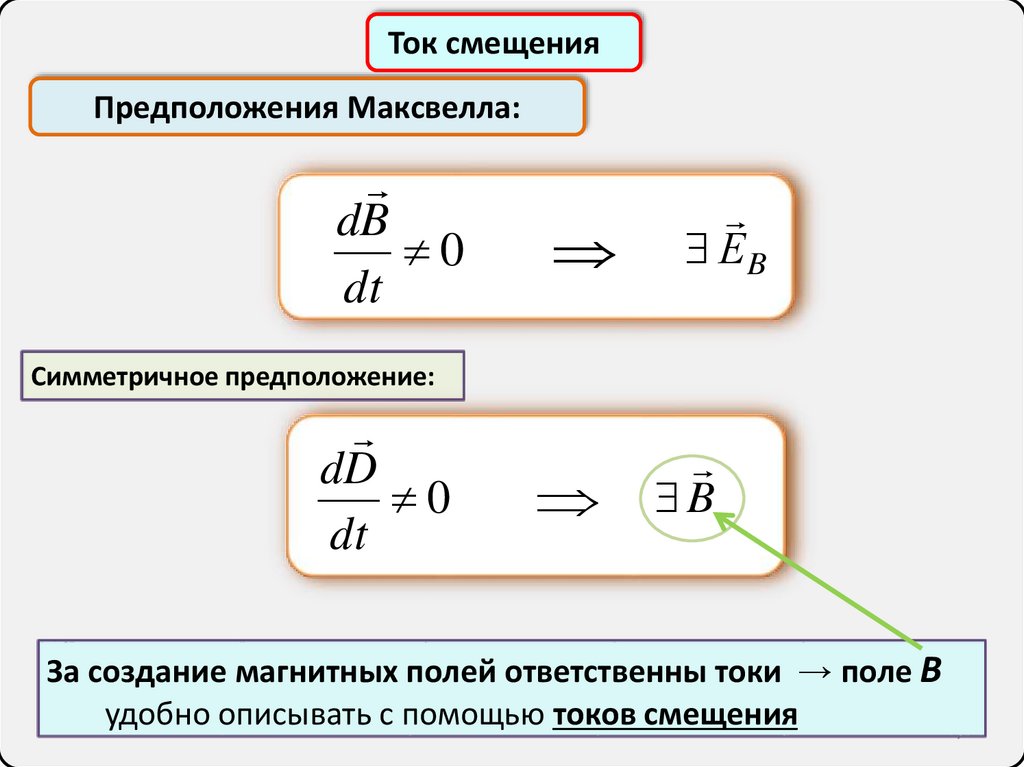
7.

Ток смещения
Предположения Максвелла:
dB
0
dt
ЕB
Симметричное предположение:
dD
0
dt
B
За создание магнитных полей ответственны токи → поле B
удобно описывать с помощью токов смещения
7

8.

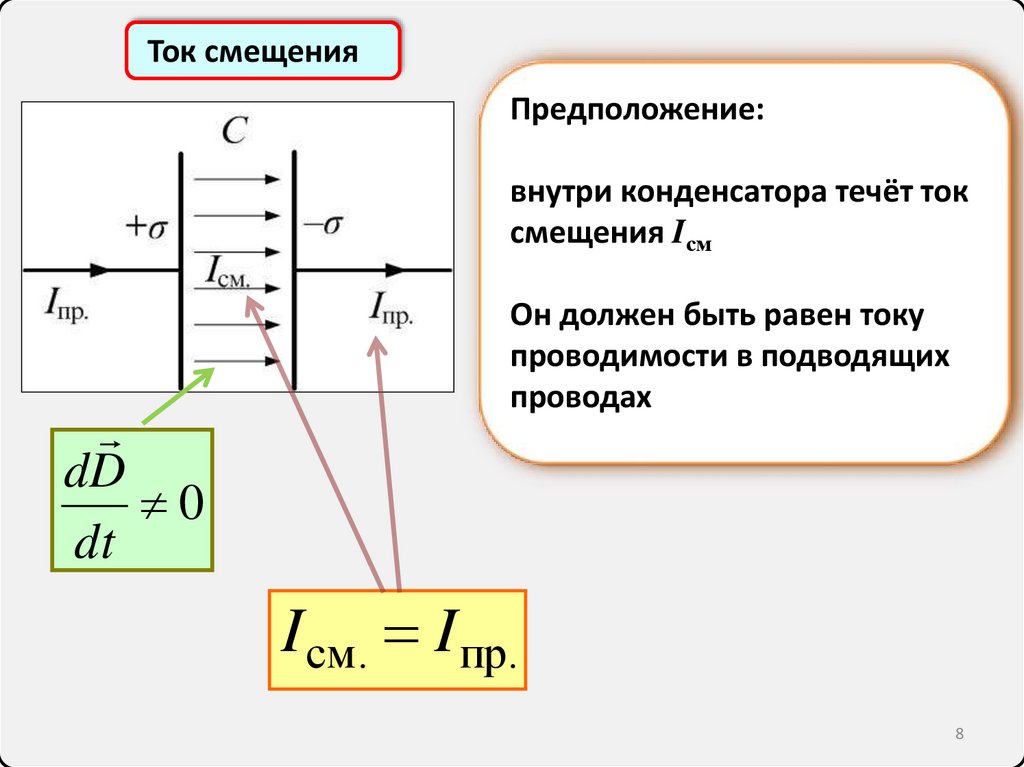
Ток смещения
Предположение:
внутри конденсатора течёт ток
смещения Iсм
dD
0
dt
Он должен быть равен току
проводимости в подводящих
проводах
I см. I пр.
8

9.

Ток смещения
I см. I пр.
q
S
dq d
d
I см.
S S
dt dt
dt
D=σ
D
I см. S
t
D
jсм.
t
9

10.

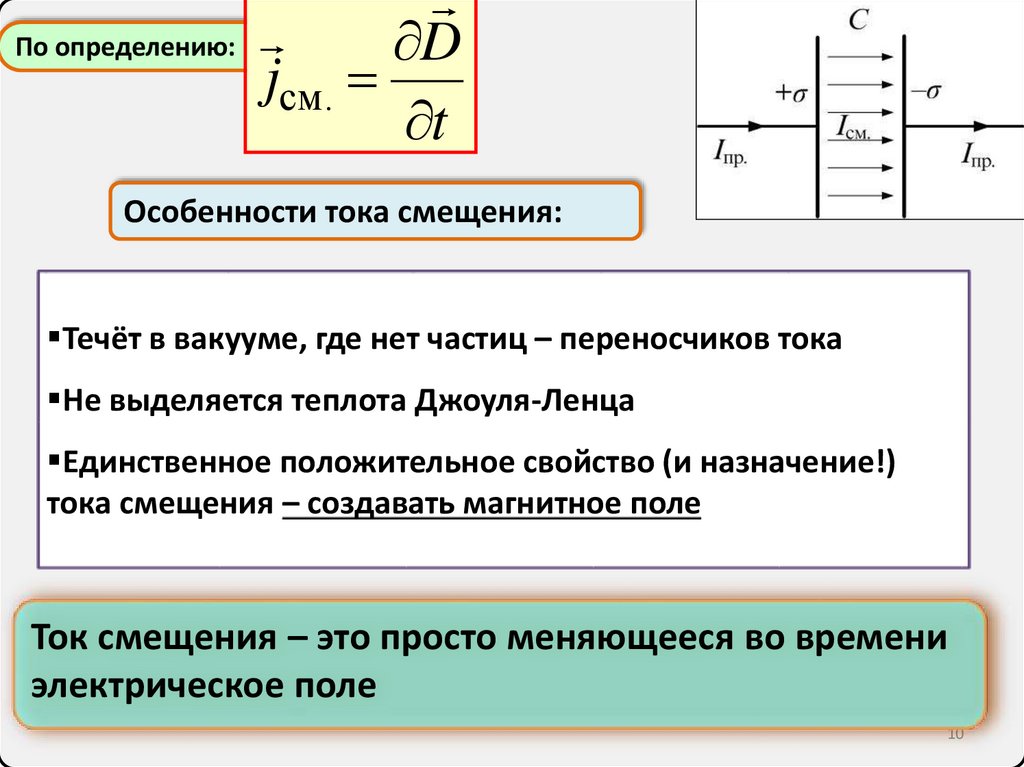
По определению:
D
jсм.
t
Особенности тока смещения:
Течёт в вакууме, где нет частиц – переносчиков тока
Не выделяется теплота Джоуля-Ленца
Единственное положительное свойство (и назначение!)
тока смещения – создавать магнитное поле
Ток смещения – это просто меняющееся во времени
электрическое поле
10

11.

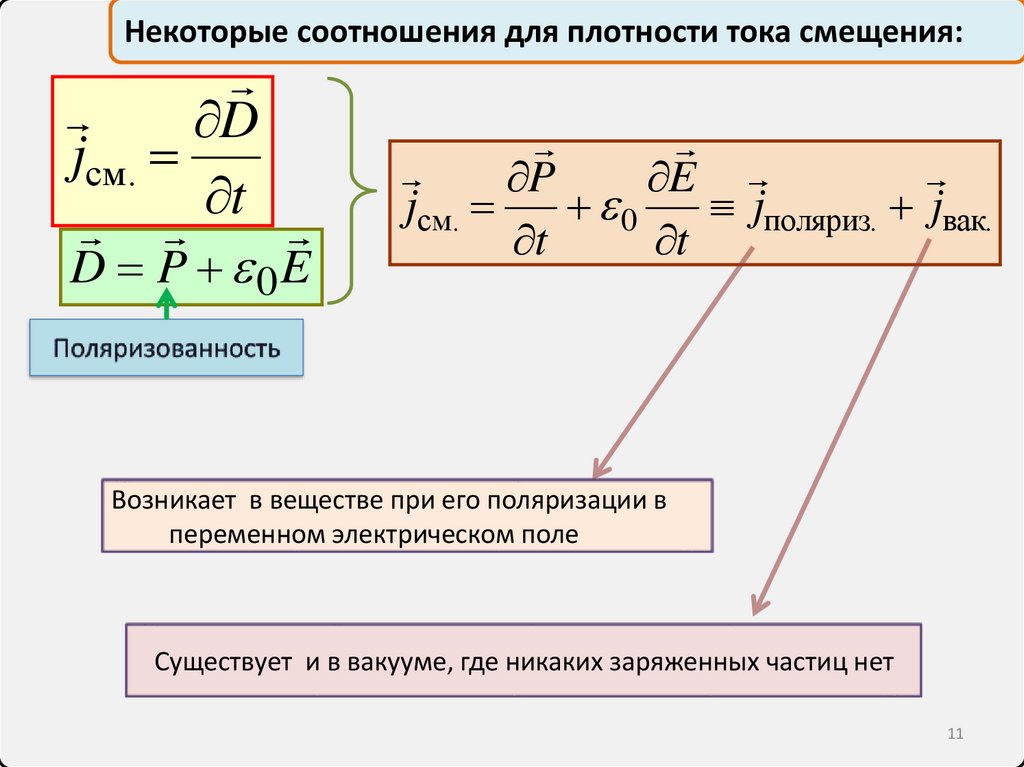
Некоторые соотношения для плотности тока смещения:
D
jсм.
t
D P 0E
P
E
jсм.
0
jполяриз. jвак.
t
t
Возникает в веществе при его поляризации в
переменном электрическом поле
Существует и в вакууме, где никаких заряженных частиц нет
11

12.

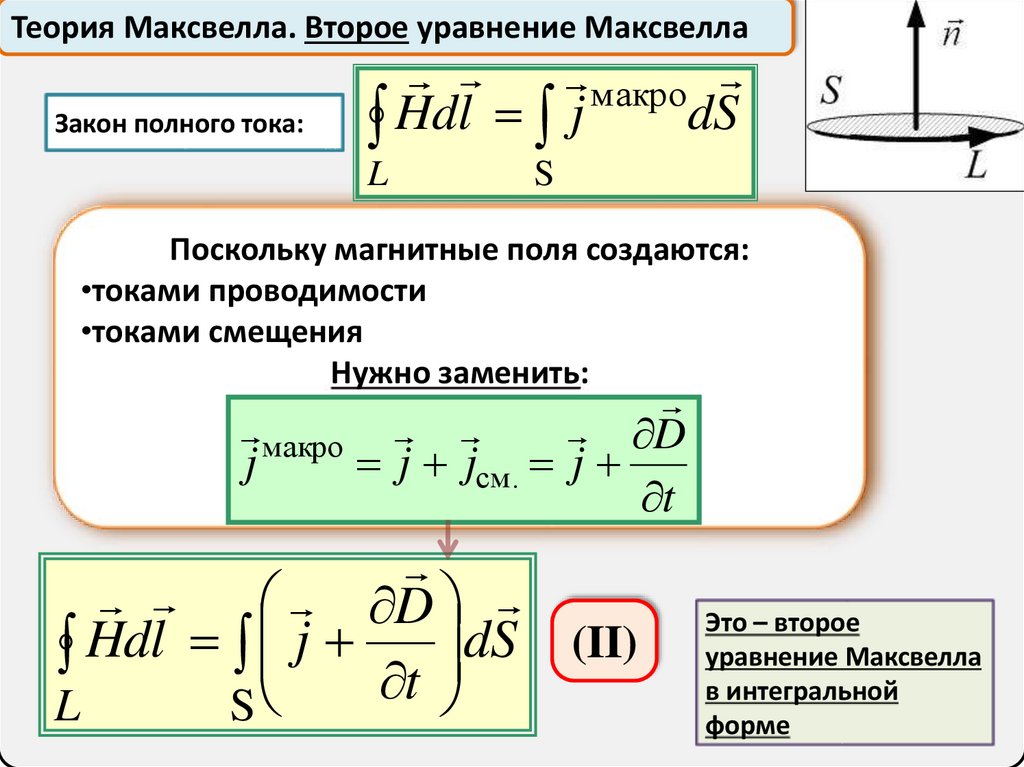
Теория Максвелла. Второе уравнение Максвелла
Закон полного тока:
макро
dS
Hdl j
L
S
Поскольку магнитные поля создаются:
•токами проводимости
•токами смещения
Нужно заменить:
макро
D
j
j jсм. j
t
D
Hdl j t dS (II)
L
S
Это – второе
уравнение Максвелла
в интегральной
форме
12

13.

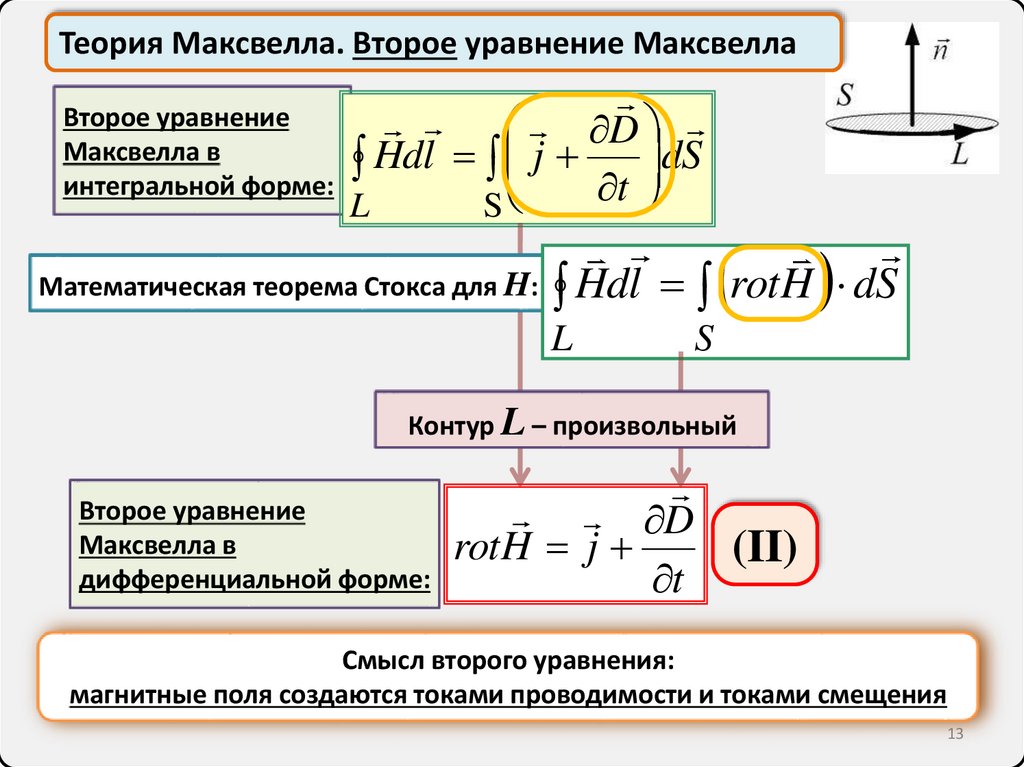
Теория Максвелла. Второе уравнение Максвелла
Второе уравнение
Максвелла в
интегральной форме:
D
Hdl j t dS
L
S
Математическая теорема Стокса для H:
Hdl rotH dS
L
S
Контур L – произвольный
Второе уравнение
Максвелла в
дифференциальной форме:
D
rotH j
(II)
t
Смысл второго уравнения:
магнитные поля создаются токами проводимости и токами смещения
13

14.

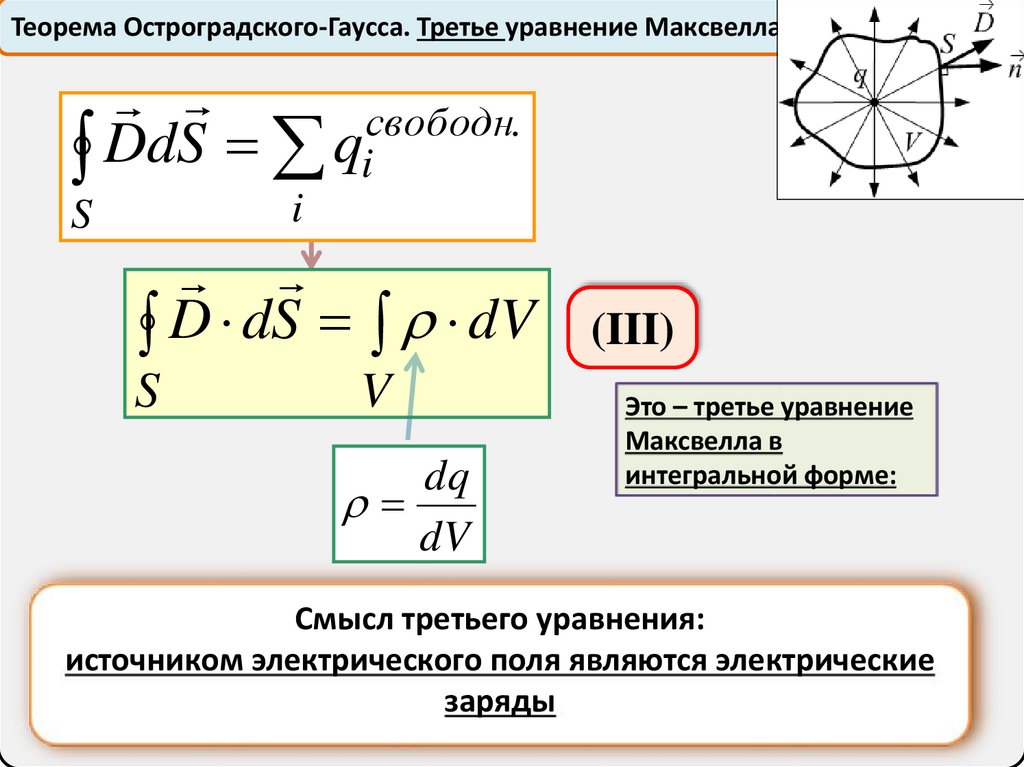
Теорема Остроградского-Гаусса. Третье уравнение Максвелла
свободн.
DdS qi
i
S
D dS dV
S
V
dq
dV
(III)
Это – третье уравнение
Максвелла в
интегральной форме:
Смысл третьего уравнения:
источником электрического поля являются электрические
заряды
14

15.

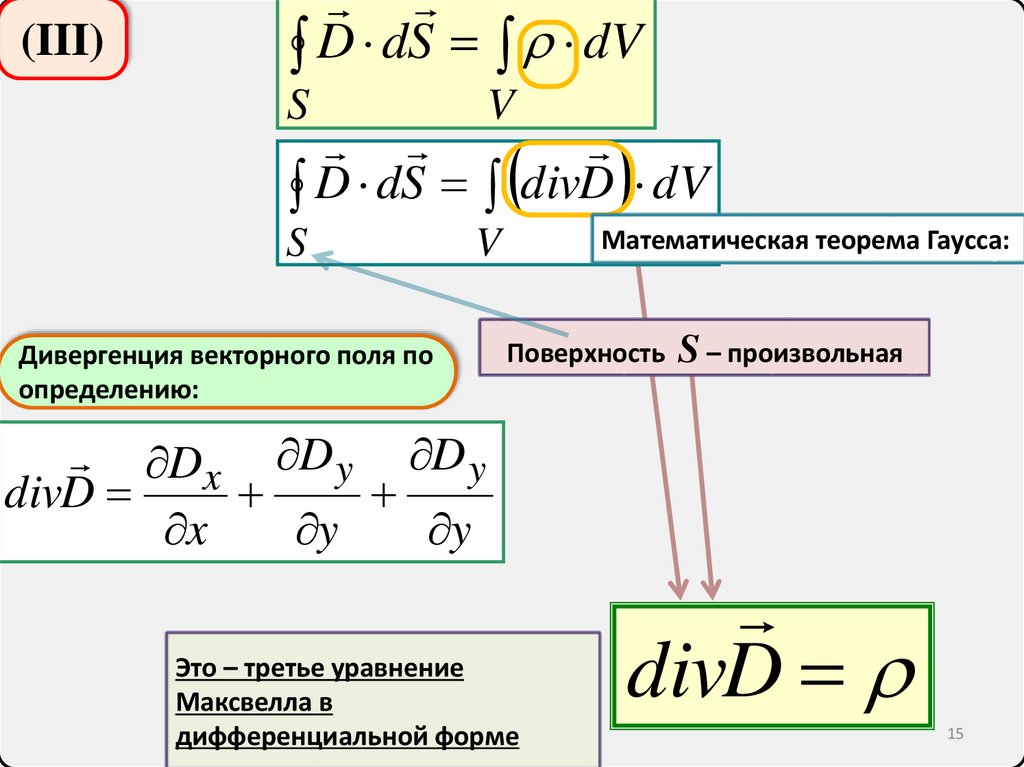
(III)
D dS dV
S
V
S
V
D dS divD dV
Дивергенция векторного поля по
определению:
Математическая теорема Гаусса:
Поверхность
S – произвольная
Dx D y D y
divD
x
y
y
Это – третье уравнение
Максвелла в
дифференциальной форме
divD
15

16.

Теорема Остроградского-Гаусса для магнитного поля
Четвёртое уравнение Максвелла
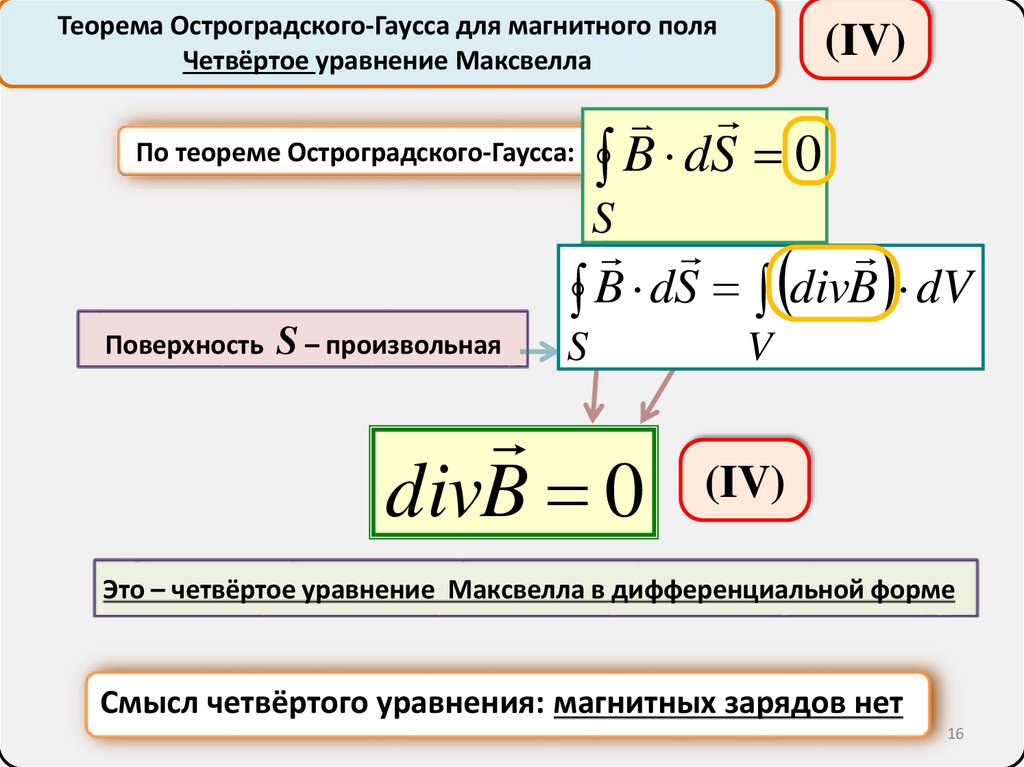
По теореме Остроградского-Гаусса:
(IV)
B dS 0
S
B dS divB dV
Поверхность
S – произвольная
S
divB 0
V
(IV)
Это – четвёртое уравнение Максвелла в дифференциальной форме
Смысл четвёртого уравнения: магнитных зарядов нет
16

17.

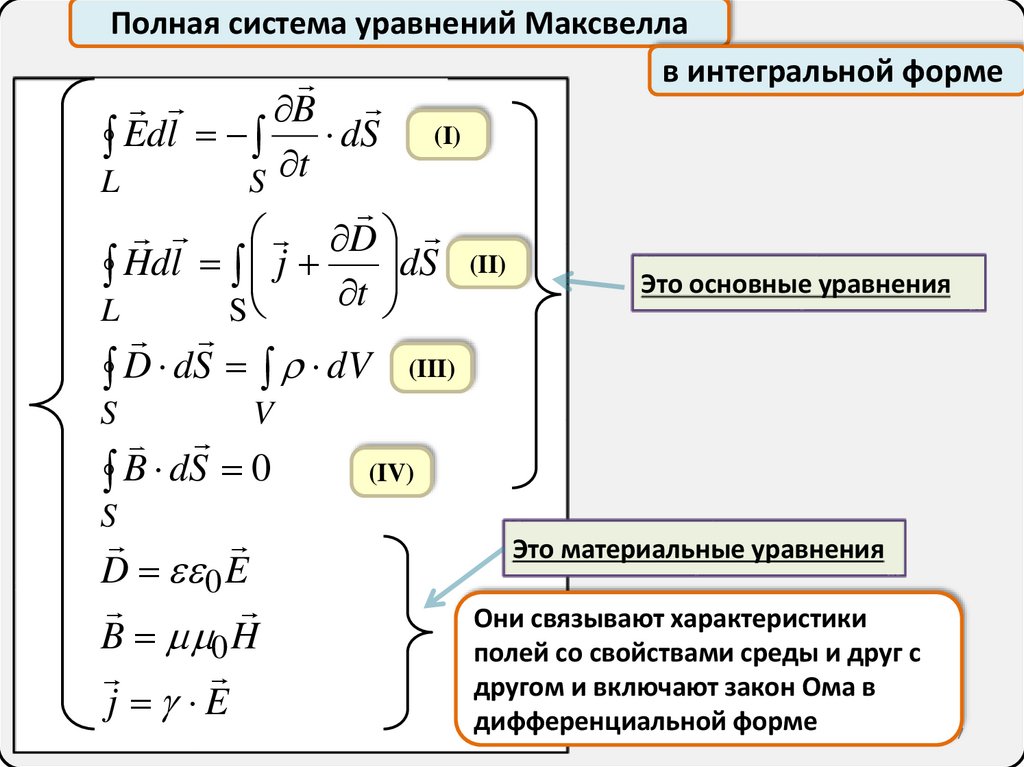
Полная система уравнений Максвелла
в интегральной форме
B
Edl t dS (I)
L
S
D
Hdl j t dS (II)
L
S
D dS dV (III)
S
Это основные уравнения
V
B dS 0
(IV)
S
D 0 E
B 0 H
j E
Это материальные уравнения
Они связывают характеристики
полей со свойствами среды и друг с
другом и включают закон Ома в
дифференциальной форме
17

18.

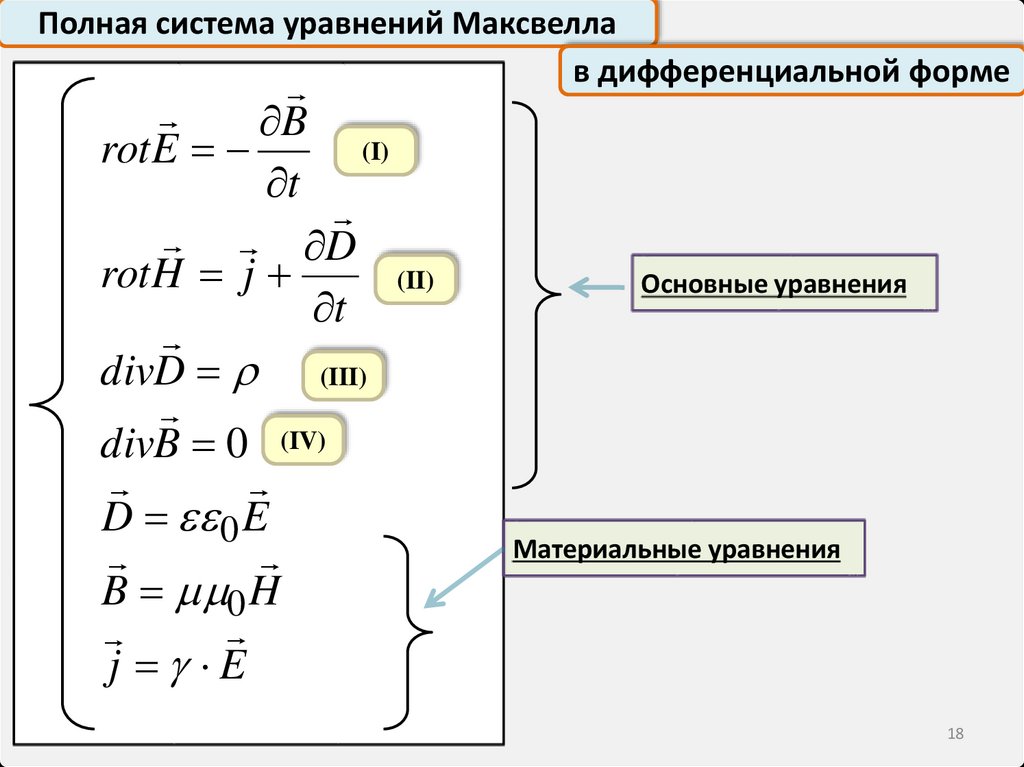
Полная система уравнений Максвелла
в дифференциальной форме
B
(I)
rot E
t
D
rot H j
(II)
t
divD (III)
divB 0 (IV)
D 0 E
B 0 H
j E
Основные уравнения
Материальные уравнения
18

19.

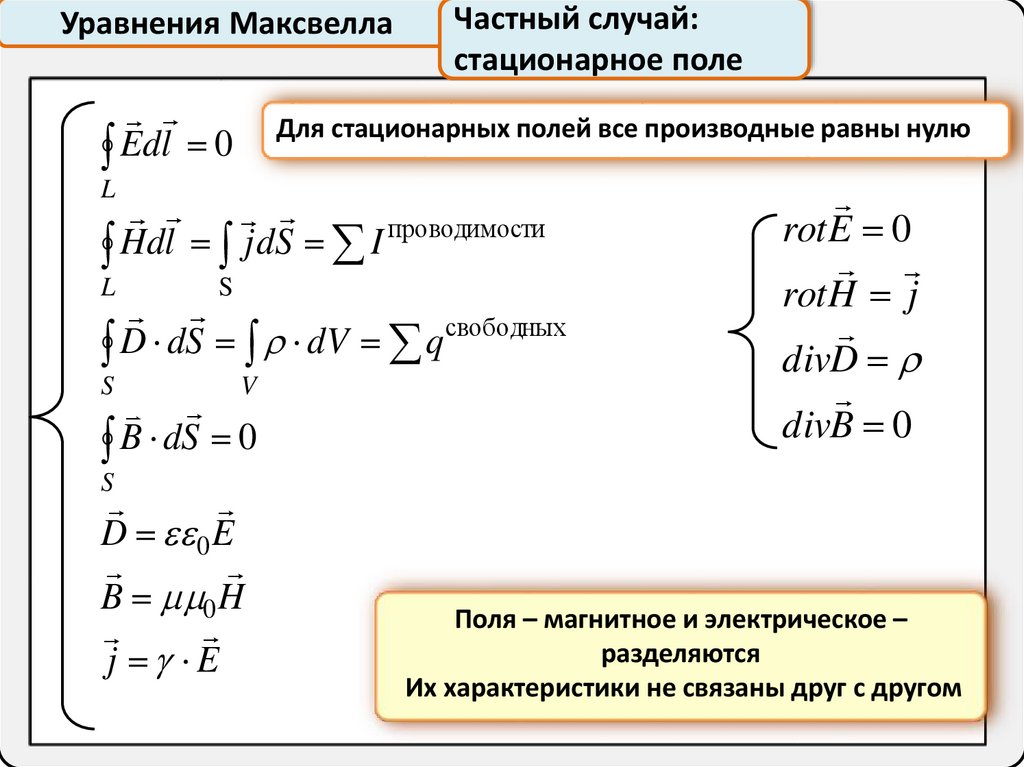
Уравнения Максвелла
Edl 0
Частный случай:
стационарное поле
Для стационарных полей все производные равны нулю
L
проводимости
H
d
l
j
d
S
I
L
S
свободных
D
d
S
dV
q
S
V
B dS 0
rot E 0
rot H j
divD
divB 0
S
D 0 E
B 0 H
j E
Поля – магнитное и электрическое –
разделяются
Их характеристики не связаны друг с другом
19

20.

Уравнения Максвелла
B
Edl t dS
L
S
D
Hdl t dS
L
S
D dS 0
S
B dS 0
S
D 0 E
B 0 H
Частный случай: поле в
свободном пространстве
В свободном пространстве нет ни
зарядов, ни токов проводимости
B
rot E
t
D
rot H
t
divD 0
divB 0
20

21.

Электромагнитное поле свободном пространстве
B
rot E
t
rot H D
t
Изменение магнитного
поля B
B
dS
Ed l
L
S t
H dl D dS
t
S
L
порождает поле
электрическое E тоже в общем случае
переменное
Изменения электрического поля D 0 E порождают
снова возникновение магнитного поля B 0 H
Это – электромагнитная волна, распространяющаяся в
свободном пространстве, в отрыве от первоначально
породивших её зарядов и токов
Поля – электрическое и магнитное – распространяются,
превращаясь друг в друга
21