Алгоритм Гопкрофта — Карпа

1. Образец заголовка

Розрахунково - графічна
робота
Образец
ГопкрофтаКарпа*”
на тему -“ Алгоритмзаголовка
Образец подзаголовка
подзаголовка
Виконав
студент групи КН-405
Зварич В. Я.

2.

Короткий опис алгоритму
Алгоритм Гопкрофта — Карпа отримує на вході дводольний граф
і видає на виході парування найбільшої потужності – множину, що
містить якнайбільше ребер з властивістю, що жодна двійка ребер не має
спільної вершини.
В основі алгоритму лежить поняття шлях розширення, шлях який
починається у вільній вершині і закінчується вільною вершиною, також він
чергує ребро з парування з ребрами, що не входять до парування.

3.

Дводольні графи
Дводольним графом називають такий граф, меожину вершин якого
можна розділити на дві підмножини так, щоб будь-які дві суміжні вершини
належали до різних підмножин.

4.

Парування
Паруванням М в графі G =(V,E) називається множина попарно
несуміжних ребер, тобто ребер, що не мають спільних вершин.
Максимальне парування – парування М, яке не є підмножиною
для будь-якого іншого парування.
Найбільше парування– парування з найбільшою можливою кількістю
ребер.
Досконале парування – парування, що покриває всі вершини графу, тобто
кожна вершина інцидентна одному з ребер. Кожне досконале парування є
найбільшим і максимальним

5.

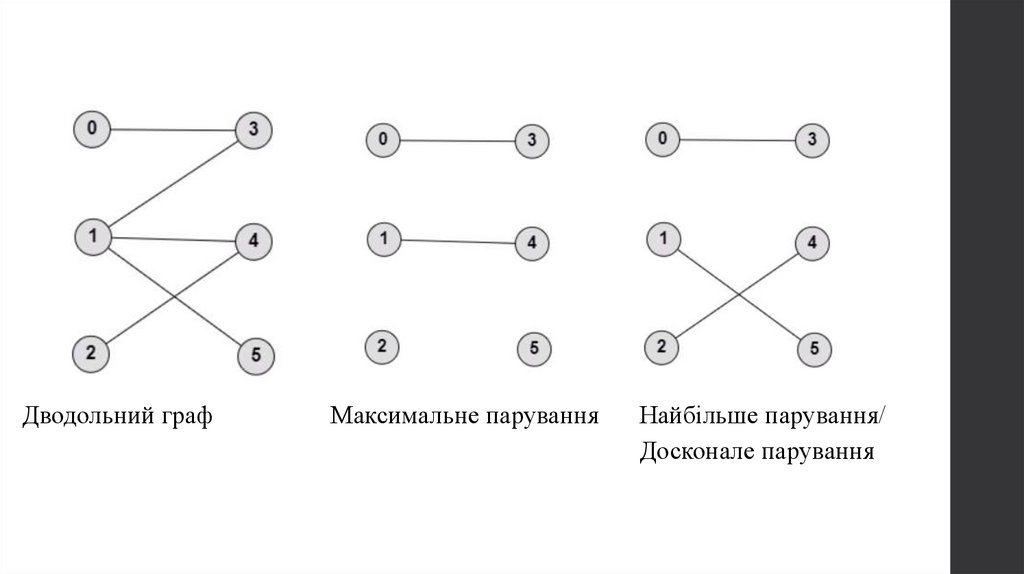
Дводольний граф
Максимальне парування
Найбільше парування/
Досконале парування

6.

Блок-схема алгоритму

7.

8.

Логічна модель проекту

9.

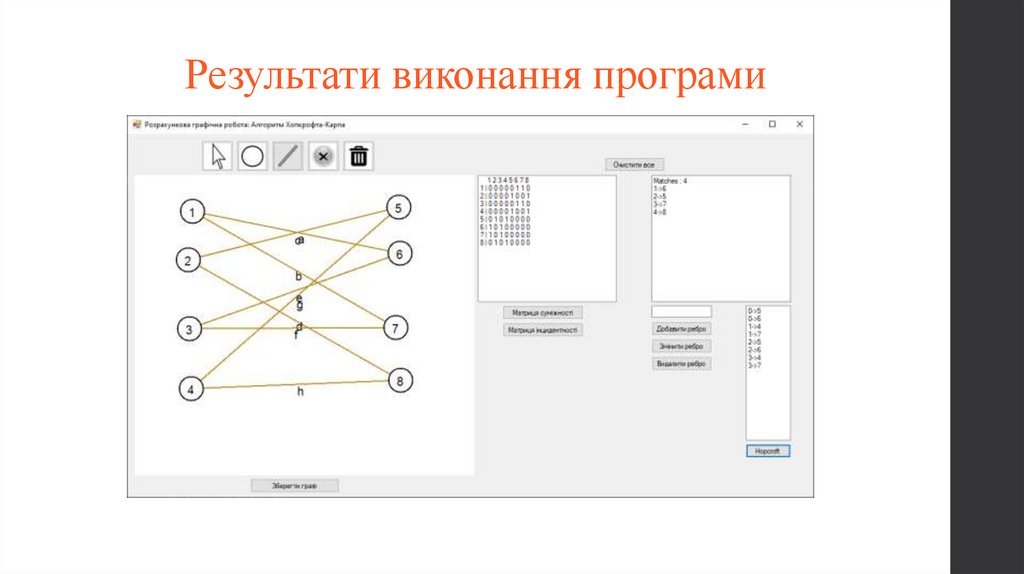
Результати виконання програми

10.

Результати виконання програми
Реалізована програма знаходить одне з можливих найбільших
парувань в дводольному графі.
Користувач малює власний граф, за потреби може отримати його
матриці суміжності чи інцидентності, натиснувши відповідні кнопки.
Коли граф повністю створено, користувач натискає кнопку для
обрахунку алгоритму, та отримує на виході результат, що складається
з числа парувань (розмір найбільшого парування) та списку ребер, що
до нього входять.

11.

Дякую за увагу!