Similar presentations:
Базові пошукові алгоритми на графах. (Лекція 2)
1. Базові пошукові алгоритми на графах
Лекція №22. Пошук у ширину
Вже розглядалися пошукові алгоритми: пошукзаданої інформації в одновимірному масиві, в
мережі, на дереві. Досліджуючи задачі, що
пов’язані з обробкою інформації, яку можна
представити у вигляді графів, також постає
питання пошуку. У першу чергу це пошук
шляху від однієї заданої вершини до іншої.
Існує два підходи до здійснення такого пошуку.
Розглянемо перший із них ― пошук у ширину.
Як відомо, одним із найпоширеніших способів
представлення графу є матриця суміжності.
Саме на перегляді цієї матриці і базується
метод пошуку у ширину.
3.
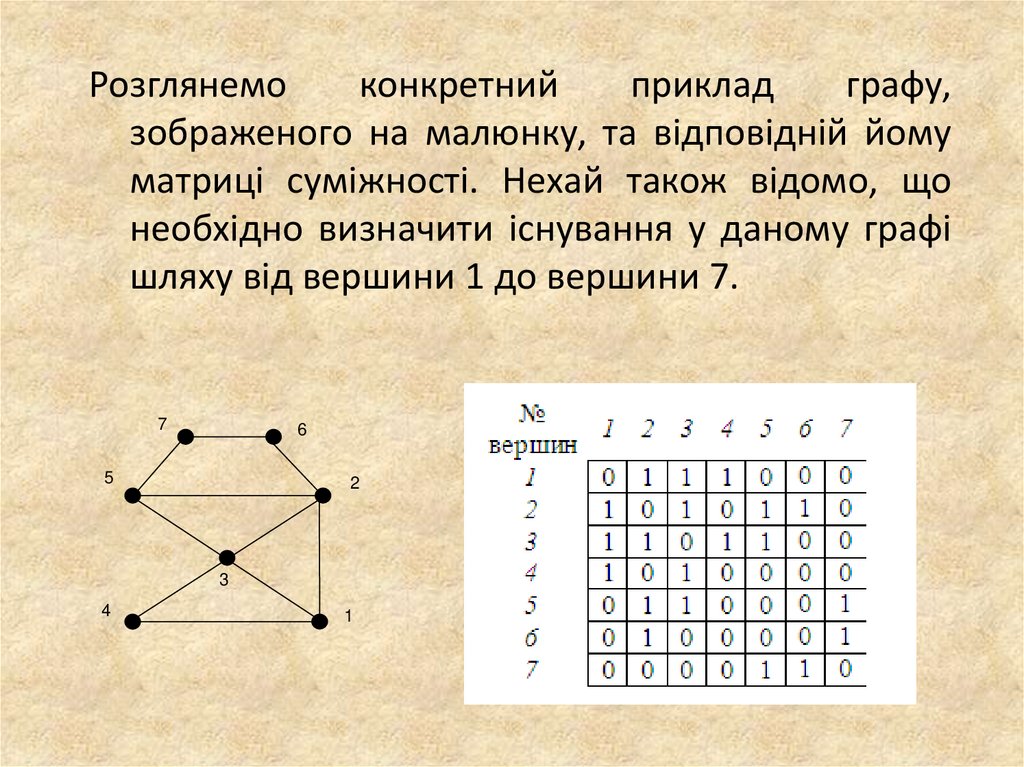
Розглянемоконкретний
приклад
графу,
зображеного на малюнку, та відповідній йому
матриці суміжності. Нехай також відомо, що
необхідно визначити існування у даному графі
шляху від вершини 1 до вершини 7.
7
6
5
2
3
4
1
4.
Почнемо пошук шуканої вершини 7із заданої вершини 1 і зафіксуємо
для цю інформацію, будуючи
дерево пошуку, у якому на
першому
кроці
пошукового
алгоритму є лише одна вершина 1
та послідовність вершин, які
переглядаються.
Встановимо
покажчики перегляду вершин у
послідовності
таким
чином:
верхній вказуватиме на номер
вершини, з якої дивимося, а
нижній ― на номер останньої
видимої вершини. Відповідно на
першому кроці такою вершиною є
єдина вершина 1.
1
1
5.
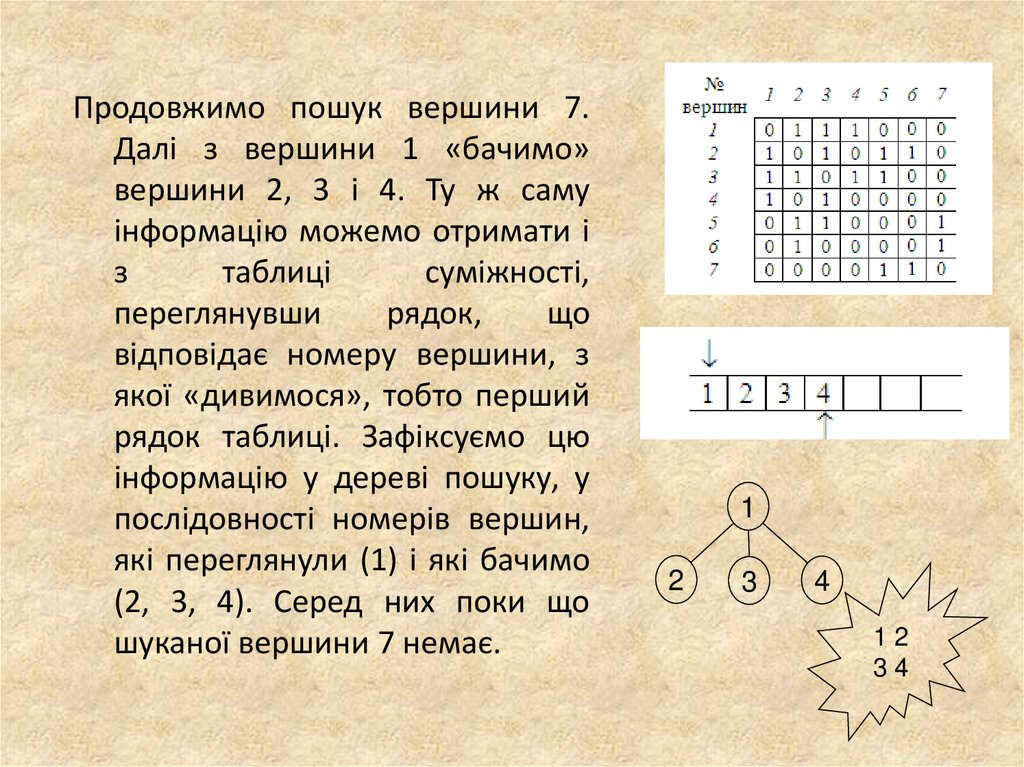
Продовжимо пошук вершини 7.Далі з вершини 1 «бачимо»
вершини 2, 3 і 4. Ту ж саму
інформацію можемо отримати і
з
таблиці
суміжності,
переглянувши
рядок,
що
відповідає номеру вершини, з
якої «дивимося», тобто перший
рядок таблиці. Зафіксуємо цю
інформацію у дереві пошуку, у
послідовності номерів вершин,
які переглянули (1) і які бачимо
(2, 3, 4). Серед них поки що
шуканої вершини 7 немає.
1
2
3
4
12
34
6.
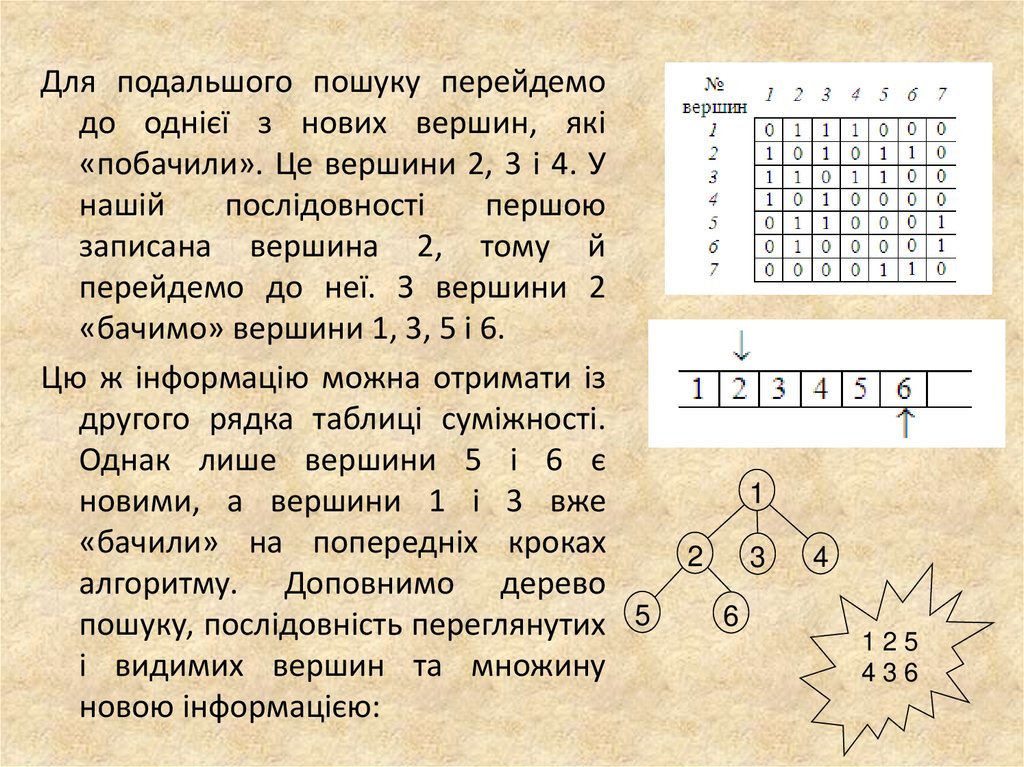
Для подальшого пошуку перейдемодо однієї з нових вершин, які
«побачили». Це вершини 2, 3 і 4. У
нашій
послідовності
першою
записана вершина 2, тому й
перейдемо до неї. З вершини 2
«бачимо» вершини 1, 3, 5 і 6.
Цю ж інформацію можна отримати із
другого рядка таблиці суміжності.
Однак лише вершини 5 і 6 є
новими, а вершини 1 і 3 вже
«бачили» на попередніх кроках
алгоритму. Доповнимо дерево
пошуку, послідовність переглянутих 5
і видимих вершин та множину
новою інформацією:
1
2
3
4
6
125
436
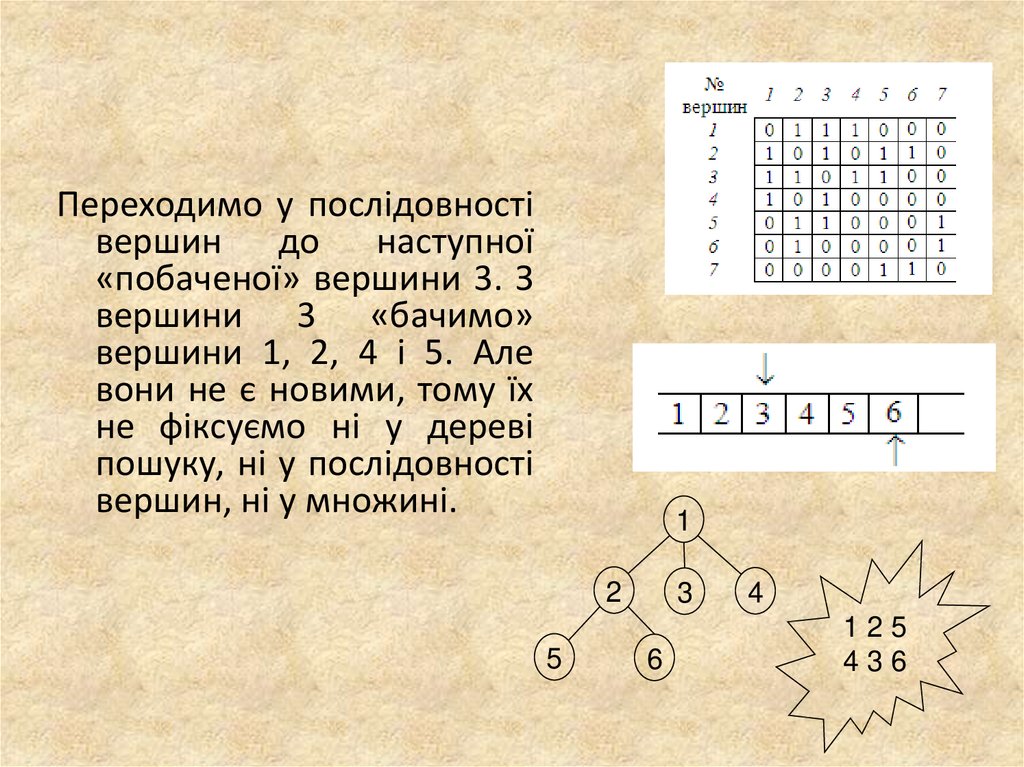
7.
Переходимо у послідовностівершин до наступної
«побаченої» вершини 3. З
вершини 3 «бачимо»
вершини 1, 2, 4 і 5. Але
вони не є новими, тому їх
не фіксуємо ні у дереві
пошуку, ні у послідовності
вершин, ні у множині.
1
2
5
3
6
4
125
436
8.
Переходимодо
наступної
вершини у послідовності, якою
є вершина 4. Звідси бачимо
вершини 1 і 3. Але і ці вершини
вже є «побаченими», тому у
нашому алгоритмі міняється
лише
вершина,
яку
переглядаємо
наступною.
Такою вершиною є вершина з
номером 4, тобто наступна у
нашій
послідовності
переглянутих
і
видимих
вершин. Із вершини 4 знову ж
таки
нічого
нового
не
побачимо, оскільки вершини 1
та 3 вже бачили раніше.
Інформація
на
малюнках
залишилася незмінною, окрім 5
переходу «голови» черги до 4го елемента.
1
2
3
6
4
125
436
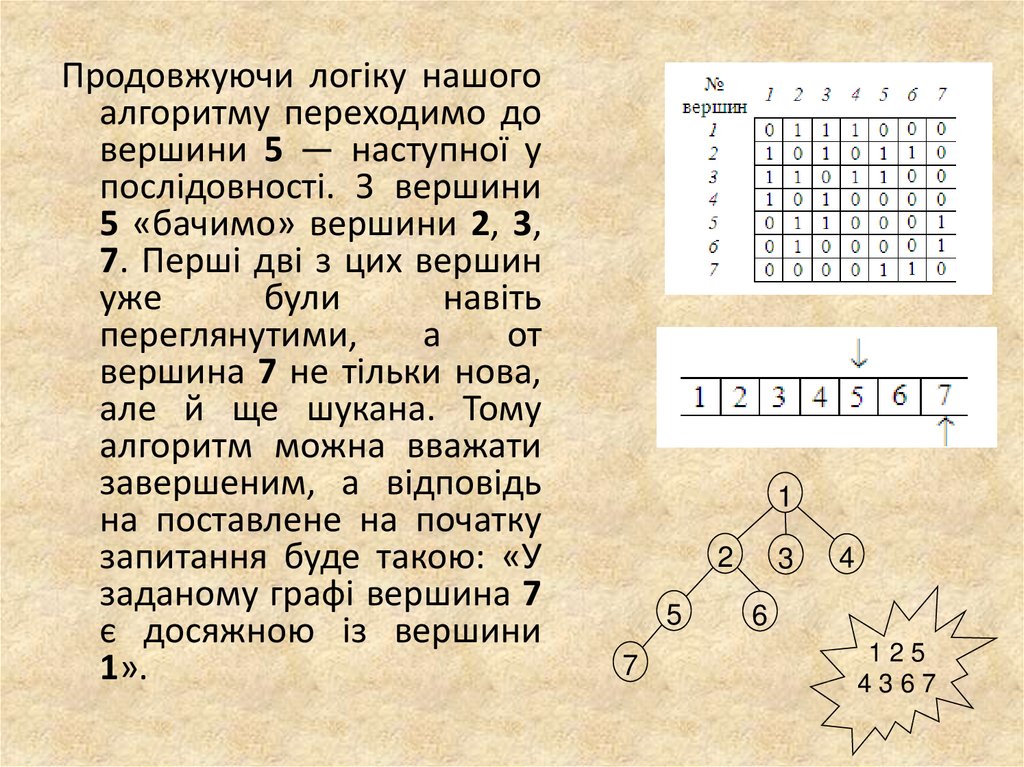
9.
Продовжуючи логіку нашогоалгоритму переходимо до
вершини 5 ― наступної у
послідовності. З вершини
5 «бачимо» вершини 2, 3,
7. Перші дві з цих вершин
уже
були
навіть
переглянутими,
а
от
вершина 7 не тільки нова,
але й ще шукана. Тому
алгоритм можна вважати
завершеним, а відповідь
на поставлене на початку
запитання буде такою: «У
заданому графі вершина 7
є досяжною із вершини
1».
1
2
5
7
3
4
6
125
4367
10.
Проаналізуємо описаний алгоритм з точки зору йогореалізації у вигляді програми. Як було вже сказано
вище, інформація про граф міститиметься у таблиці
суміжності або ж у списку суміжності.
Інформація про переглянуті і побачені вершини ― в
одновимірному масиві. Алгоритм обробки цього
масиву відповідає роботі зі структурою даних
«черга», де «голова» черги вказує на поточну
вершину, з якої дивимося далі, а «хвіст» вказує на
останню видиму вершину.
Під час виконання алгоритму «голова» переміщується
вправо на нову вершину, в яку переходимо для
подальшого перегляду нових вершин, а «хвіст»
також переміщується вправо одночасно із
дописуванням нових видимих вершин.
11.
Тепер можна проаналізувати умови завершення роботиалгоритму пошуку у ширину.
Таких випадків є два:
• шукана вершина знайдена і відомий шлях до неї та шукана
вершина є недосяжною;
• шлях до неї відсутній.
Розглянуто саме перший випадок пошуку вершини у графі,
коли шукана вершина 7 є досяжною із заданої вершини 1.
Шлях від вершини 1 до вершини 7 присутній у черзі, але
без додаткової інформації він дещо прихований. Для
отримання цього шляху необхідно запам’ятовувати також і
номери вершин, з яких «побачили» кожну наступну
вершину. На малюнку ця інформація позначена індексами
для кожної поточної вершини, записаної у чергу.
12.
Другий випадок може бути розтлумачений таким чином:«голова» черги досягнула її «хвоста», а серед нових
«побачених» вершин так і не з’явилася шукана. Це
означає, що переглянуті всі досяжні вершини графа, але
шукана не досягнута.
Підсумок розглянутого методу.
По-перше, зрозуміло, чому цей метод носить назву «пошук в
ширину». Адже дійсно здійснюється пошук шуканої
вершини, розглядаючи на кожному новому кроці
одночасно всі нові вершини, які ще не бачили.
По-друге, можна зробити висновок, що метод пошуку в
ширину дає найкоротший шлях від заданої вершини до
шуканої.
13.
Проведемо оцінку алгоритму пошуку у ширину.При формуванні черги з вершин заданого
графа, що складається з n вершин і m ребер,
кожна вершина переглядається лише один
раз. Це відповідає оцінці O(n).
Але при цьому переглядаються всі ребра, яким
належить поточна вершина. Отже оцінка
перегляду ребер становить О(m).
Оскільки перегляд ребер іде паралельно з
переглядом вершин, що їм належать, то
остаточна оцінка алгоритму визначається як
О(n+m) О(max(n,m))=O(m).
Отже, можна зробити висновок, що час роботи
алгоритму прямо пропорційний розміру
заданого графа.
14. Пошук у глибину
Якщо під час пошуку у ширину захоплювали усі новівершини, що було видно із поточної вершини, у яку
переміщувалися на кожному наступному кроці, то
під час пошуку у глибину дещо змінимо стратегію.
На кожному кроці алгоритму, знаходячись у наступній
поточній вершині, будемо «бачити» лише одну нову
досі невидиму вершину і переходити до неї.
Розглянемо той самий граф, що і у попередньому
випадку, і його таблицю суміжності. Будемо знову
шукати шлях від вершини 1 до вершини 7. Під час
пошуку будемо так само, як у і попередньому
алгоритмі, будувати дерево пошуку, послідовність
переглянутих і нових видимих вершин та множину
відвіданих вершин.
15.
На малюнку зображеноперший крок нашого
алгоритму,
який
повністю збігається з
першим
кроком
алгоритму пошуку у
ширину.
1
1
16.
Наступний крок будетаким: згідно таблиці
суміжності
першою
новою вершиною, яку
«бачимо» із вершини
1 є вершина 2.
Перейдемо до неї,
додавши її у дерево
пошуку,
у
послідовність
відвіданих вершин і у
множину.
1
2
12
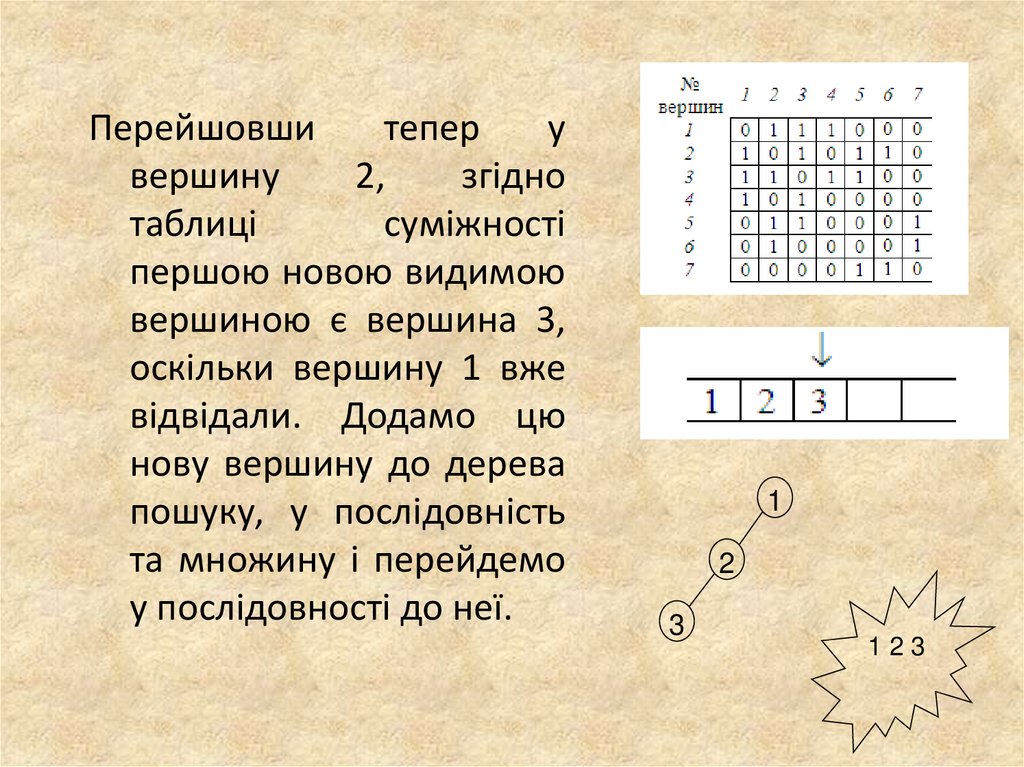
17.
Перейшовшитепер
у
вершину
2,
згідно
таблиці
суміжності
першою новою видимою
вершиною є вершина 3,
оскільки вершину 1 вже
відвідали. Додамо цю
нову вершину до дерева
пошуку, у послідовність
та множину і перейдемо
у послідовності до неї.
1
2
3
123
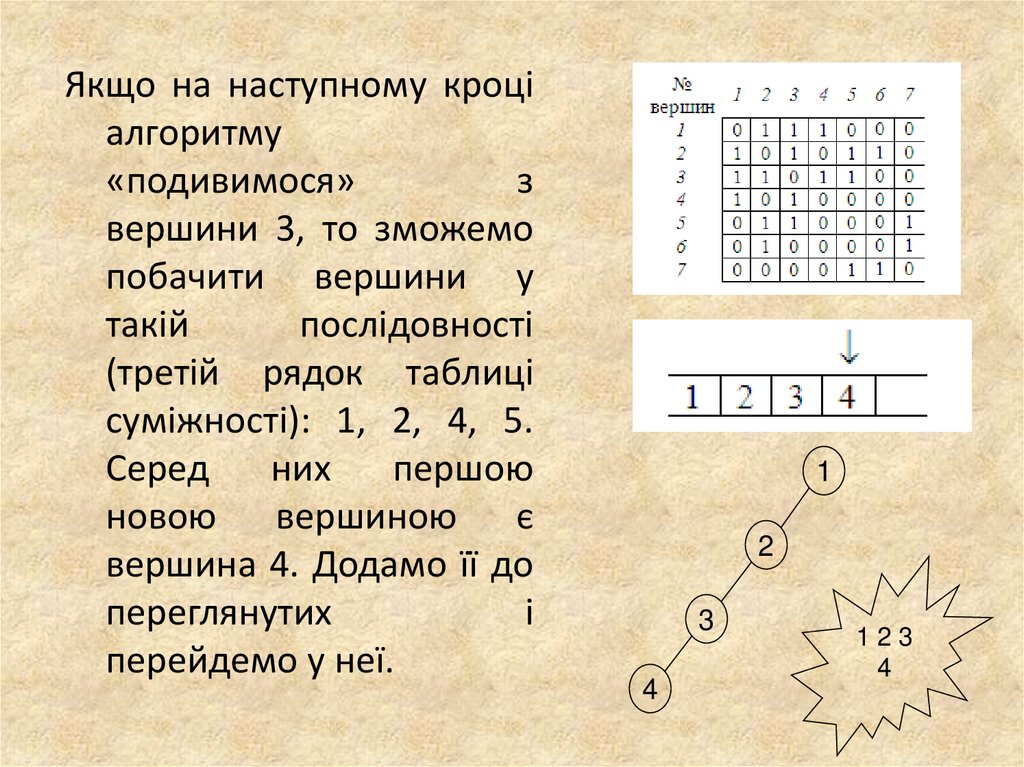
18.
Якщо на наступному кроціалгоритму
«подивимося»
з
вершини 3, то зможемо
побачити вершини у
такій
послідовності
(третій рядок таблиці
суміжності): 1, 2, 4, 5.
Серед
них
першою
новою вершиною є
вершина 4. Додамо її до
переглянутих
і
перейдемо у неї.
1
2
3
4
123
4
19.
Що нового ми «побачимо» звершини
4?
Побачимо
вершини 1 і 3. Але жодна з них
не є новими. Цю ситуацію
можна тлумачити як тупик.
Однак з попереднього методу
пошуку відомо, що під час
пошуку у ширину знайдена
позитивна відповідь. Можливо
визначений не той шлях і треба
спробувати
повернутися
назад?
Попередньою
вершиною була вершина 3 і
саме до неї повернемося.
1
2
3
4
123
4
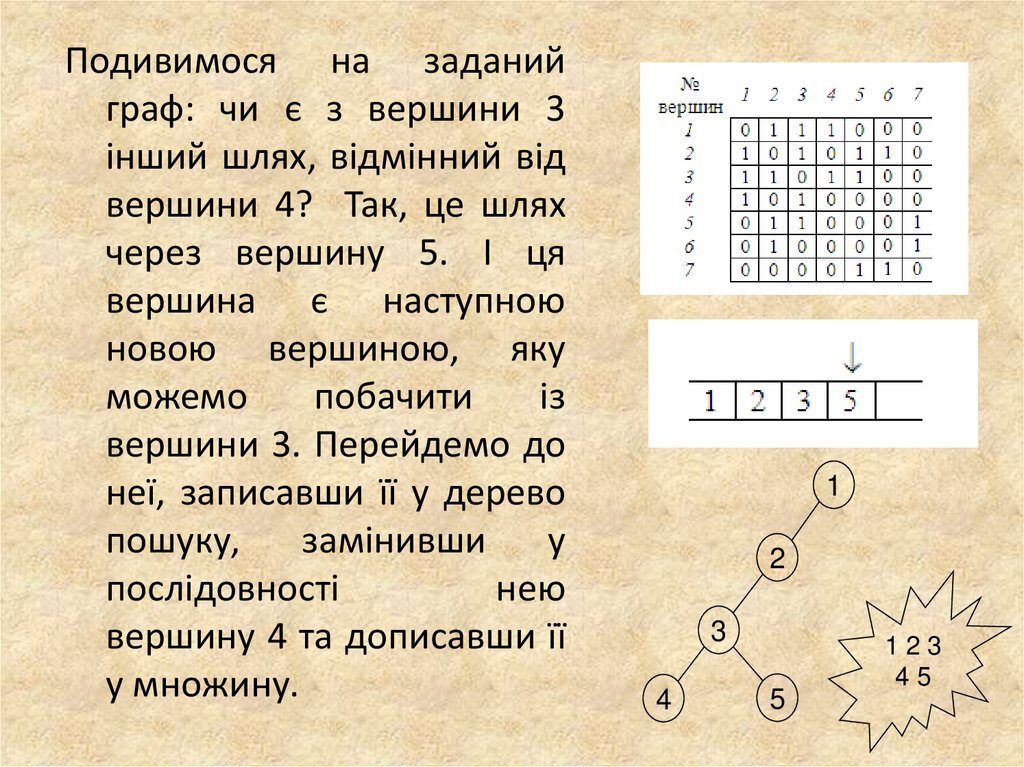
20.
Подивимося на заданийграф: чи є з вершини 3
інший шлях, відмінний від
вершини 4? Так, це шлях
через вершину 5. І ця
вершина є наступною
новою вершиною, яку
можемо
побачити
із
вершини 3. Перейдемо до
неї, записавши її у дерево
пошуку,
замінивши
у
послідовності
нею
вершину 4 та дописавши її
у множину.
1
2
3
4
5
123
45
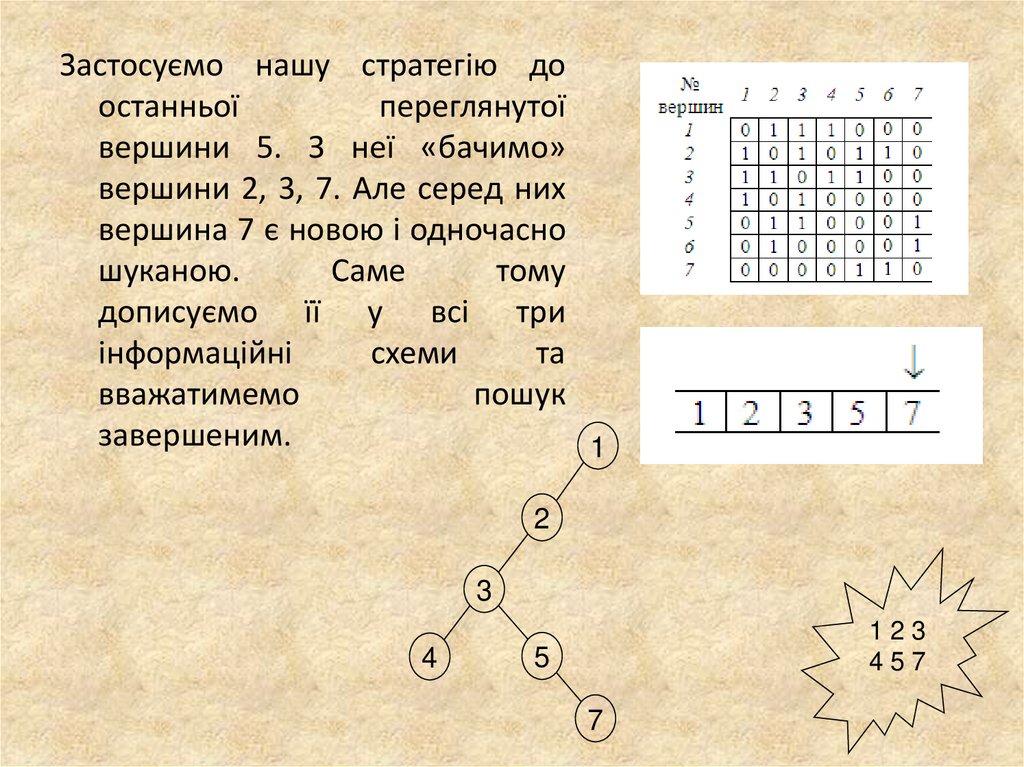
21.
Застосуємо нашу стратегію доостанньої
переглянутої
вершини 5. З неї «бачимо»
вершини 2, 3, 7. Але серед них
вершина 7 є новою і одночасно
шуканою.
Саме
тому
дописуємо її у всі три
інформаційні
схеми
та
вважатимемо
пошук
завершеним.
1
2
3
4
123
457
5
7
22.
Відповідь знайдена за допомогою алгоритму пошуку у глибину: узаданому графі вершина 7 є досяжною з вершини 1 і шлях до
неї міститься у послідовності, зображеній на малюнку.
Дивлячись на графічний малюнок, де зображено досліджуваний
граф, можна переконатися, що це дійсно шлях від вершини 1
до вершини 7. Однак отримана відповідь не збігається з
відповіддю, отриманою за допомогою алгоритму пошуку у
ширину.
Як видно із покрокового виконання описаного алгоритму, весь час
працюємо з таблицею суміжності, беручи звідти інформацію
про нову «видиму» із поточної вершину графа. Ці нові вершини
записуються у послідовність, яка обробляється за алгоритмом
роботи зі стеком: дописуємо нову інформацію в кінець цієї
послідовності, і, у разі попадання у тупик, повертаємося до її
передостаннього елемента, не розглядаючи надалі останній
записаний елемент послідовності. І на останок: для
запобігання повернення у тупикові вершини, інформацію про
всі відвідані вершини зберігатимемо у множині.
23.
Розглянуто алгоритм пошуку у глибину на прикладіграфа, де шукана вершина є досяжною із заданої, і
отримали позитивну відповідь стосовно існування
шляху між цими двома вершинами.
Як дізнатися, що шлях відсутній? Коли попадали у тупик,
то поверталися до попередньої переглянутої
вершини і намагалися знайти іншу нову ще не
«побачену» вершину. У разі відсутності шляху між
двома заданими вершинами завершимо перегляд
усіх записаних у стек вершин, повертаючись кожного
разу до попередньої, спорожнивши тим самим стек.
Отож, ознакою відсутності шляху у графі між двома
заданими вершинами є те, що на деякому кроці
алгоритму стек стане порожнім.
24.
Порівняємо два пошукових методи на графах.Спочатку відповімо на таке слушне запитання:
«Чому у наведеному прикладі графа отримані
різні відповіді, хоча кожна з них і є правильною?».
А це відбулося тому, що для методів обрані різні
стратегії: під час пошуку у ширину послідовно
переглядалися усі видимі вершини і таким чином
якнайшвидше досягнуто шукану вершину, а під
час пошуку у глибину на кожному кроці
переглядалася лише одна нова вершина і тому
можна піти у хибному напрямку.
Висновок: алгоритм пошуку у ширину завжди
визначає найкоротший шлях між двома
заданими вершинами графу.
25.
На запитання «Який з методів краще?» однозначновідповісти неможливо. Стосовно реалізації методів
можливо пошук у глибину простіший, оскільки
одразу ж отримуємо шуканий шлях, та й при
організації роботи зі стеком виникає менше
помилок.
Однак цей метод не завжди визначає найкоротший
шлях між заданими вершинами. І відповідь про
відсутність шляху у разі використання пошуку у
ширину може бути отримана швидше, ніж під час
пошуку у глибину. Однак реалізація алгоритму
пошуку у ширину вимагає організації такої
структури даних як черга і більш складної стратегії
визначення
шляху
між
двома
заданими
вершинами.
26.
Застосовування алгоритмів.По-перше, це пряме їх використання щодо
визначення шляху між двома заданими
вершинами графу.
По-друге, за допомогою пошукових алгоритмів
на графах можна визначати їх зв’язність.
По-третє, і головне, саме на цих алгоритмах
базуватимуться
деякі
з
наступних
алгоритмів, які надалі розглядатимуться.
Оцінка ефективності роботи алгоритму пошуку у
глибину така сама, як і для пошуку у ширину і
становить О(n+m) О(max(n,m))=O(m).

















 informatics
informatics