Графи та їх різновиди

1. Графи та їх різновиди

ГРАФИ ТА ЇХ РІЗНОВИДИ

2.

План
Основи теорії графів
Види графів

3.

Теорія графів — розділ
математики, що дає
змогу формалізувати
взаємозв'язки між
різноманітними видами
інформації, організувати
абстрактне їх
представлення.
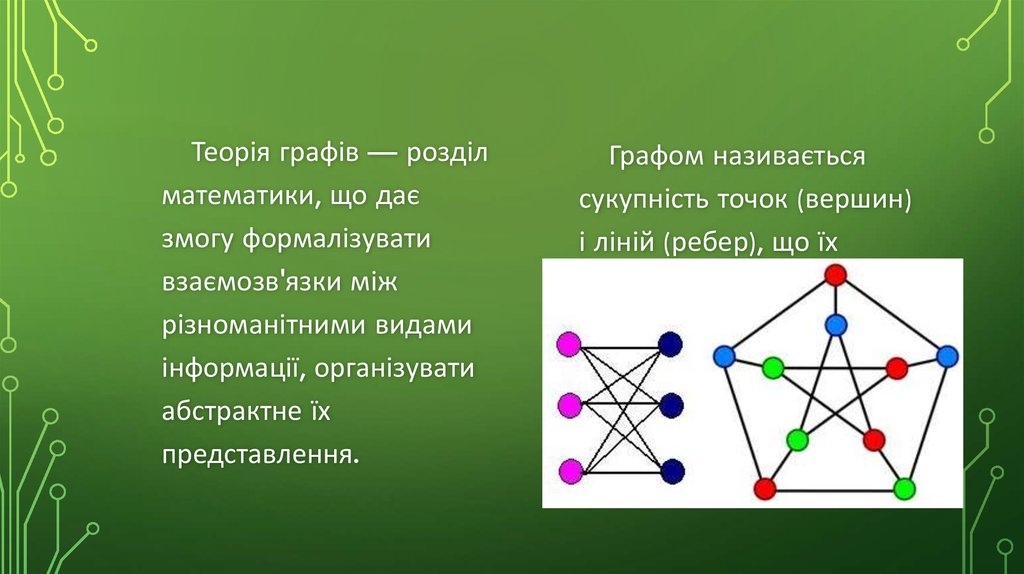
Графом називається
сукупність точок (вершин)
і ліній (ребер), що їх
з'єднують.

4.

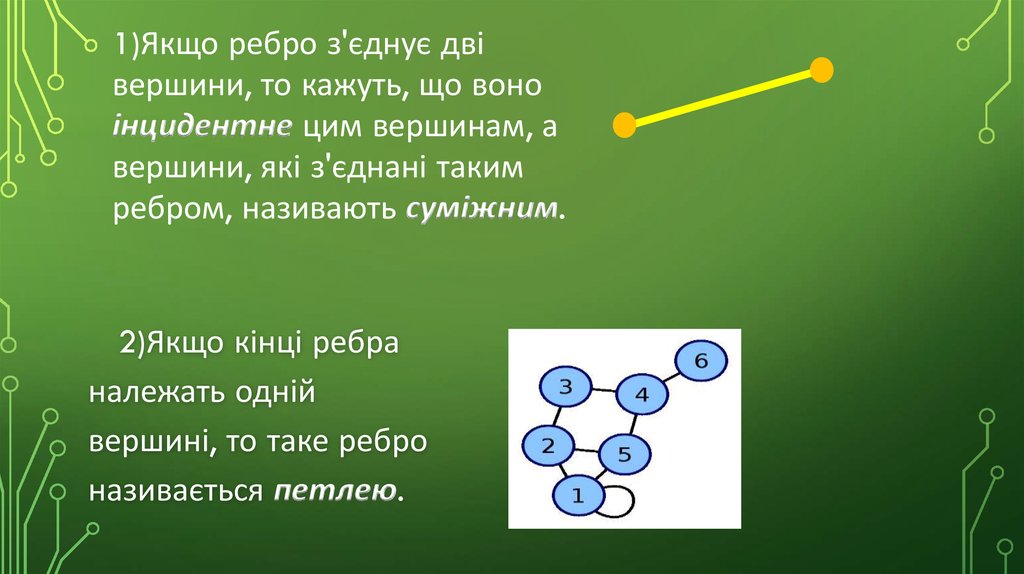
1)Якщо ребро з'єднує дві
вершини, то кажуть, що воно
інцидентне цим вершинам, а
вершини, які з'єднані таким
ребром, називають суміжним.
2)Якщо кінці ребра
належать одній
вершині, то таке ребро
називається петлею.

5.

3)Вершини, які не належать
кінцям жодного з ребер у графі,
називаються ізольованими.
Вершина А – приклад
ізольованої вершини.
А

6.

НУЛЬ - ГРАФ
ПОРОЖНІЙ ГРАФ
ПОВНИЙ ГРАФ
ПЛОСКИЙ ГРАФ
ЗВ’ЯЗНИЙ ГРАФ
ДЕРЕВО
ЗМІШАНИЙ ГРАФ
ЛІС
ГРАФ,ЯК
КОНФІГУРАЦІЯ
ОРІЄНТОВАНИЙ ГРАФ
НЕОГРАФ
ОРГРАФ
ЕЙЛЕРІВ ГРАФ
ЗВАЖЕНИЙ ГРАФ
ЗВ’ЯЗНИЙ ГРАФ ЗА
ОЙЛЕРОМ

7. Нуль-граф

НУЛЬ-ГРАФ
Граф, який складається лише з
ізольованих вершин, називається
нуль-графом.
В графі ребро без вершин
існувати не може.

8. Порожній граф

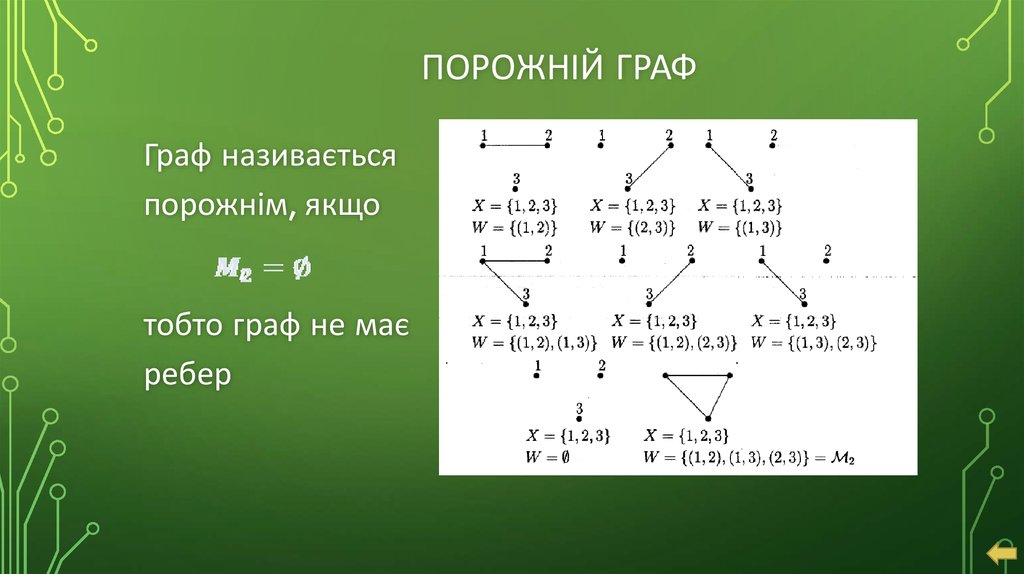
ПОРОЖНІЙ ГРАФ
Граф називається
порожнім, якщо
,
тобто граф не має
ребер

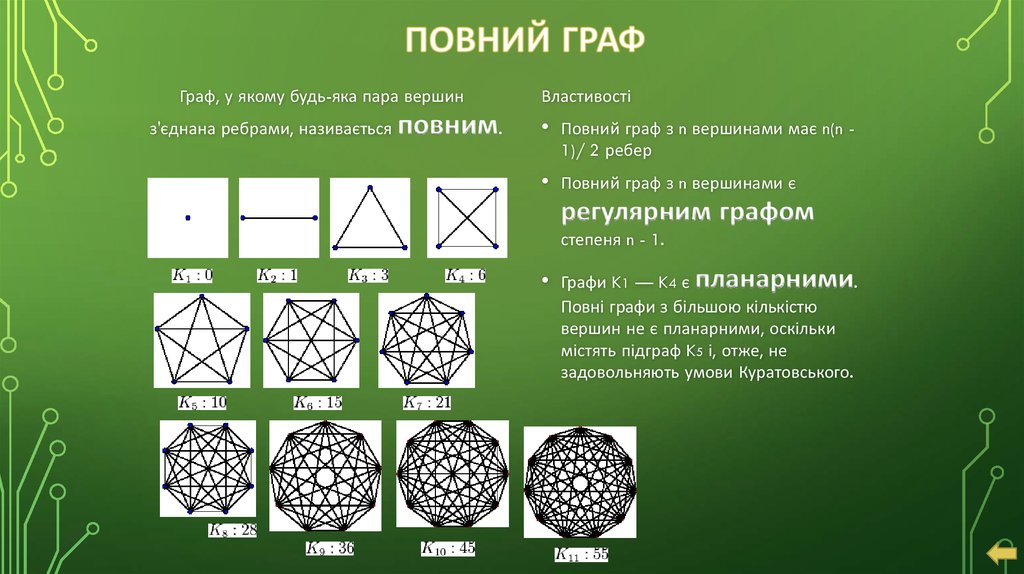
9. Повний граф

Граф, у якому будь-яка пара вершин
з'єднана ребрами, називається
повним.
Властивості
• Повний граф з n вершинами має n(n 1)/ 2 ребер
• Повний граф з n вершинами є
регулярним графом
степеня n - 1.
• Графи K1 — K4 є планарними.
Повні графи з більшою кількістю
вершин не є планарними, оскільки
містять підграф K5 і, отже, не
задовольняють умови Куратовського.

10. Плоский граф

ПЛОСКИЙ ГРАФ
Якщо всі вершини і ребра
графа знаходяться в одній
площині, то він називається
плоским, у протилежному
випадку – просторовим.

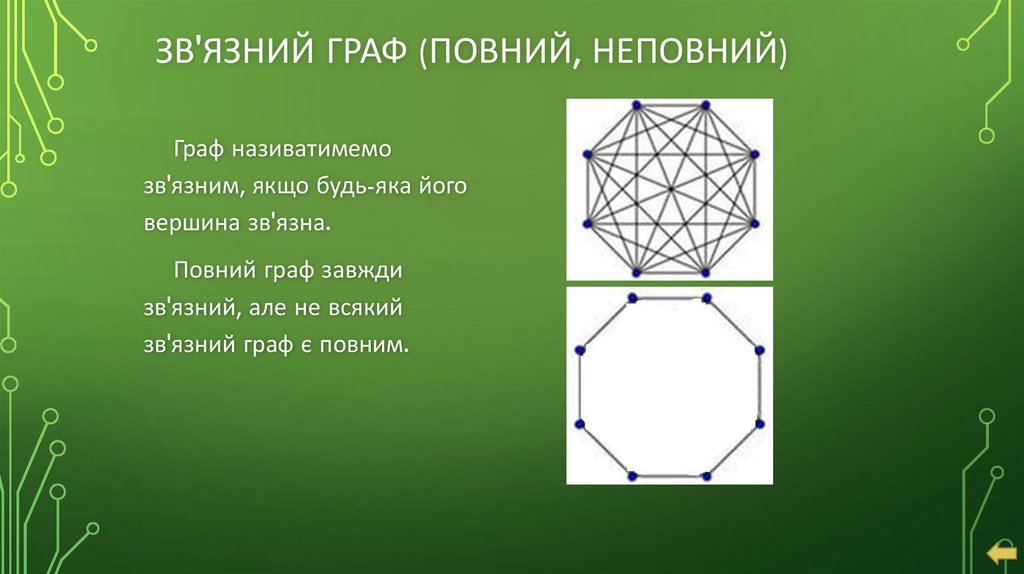
11. Зв'язний граф (повний, неповний)

ЗВ'ЯЗНИЙ ГРАФ (ПОВНИЙ, НЕПОВНИЙ)
Граф називатимемо
зв'язним, якщо будь-яка його
вершина зв'язна.
Повний граф завжди
зв'язний, але не всякий
зв'язний граф є повним.

12. Дерево

ДЕРЕВО
Граф, який немає жодного
циклу, називається
деревом.
Граф-дерево Фібоначчі

13.

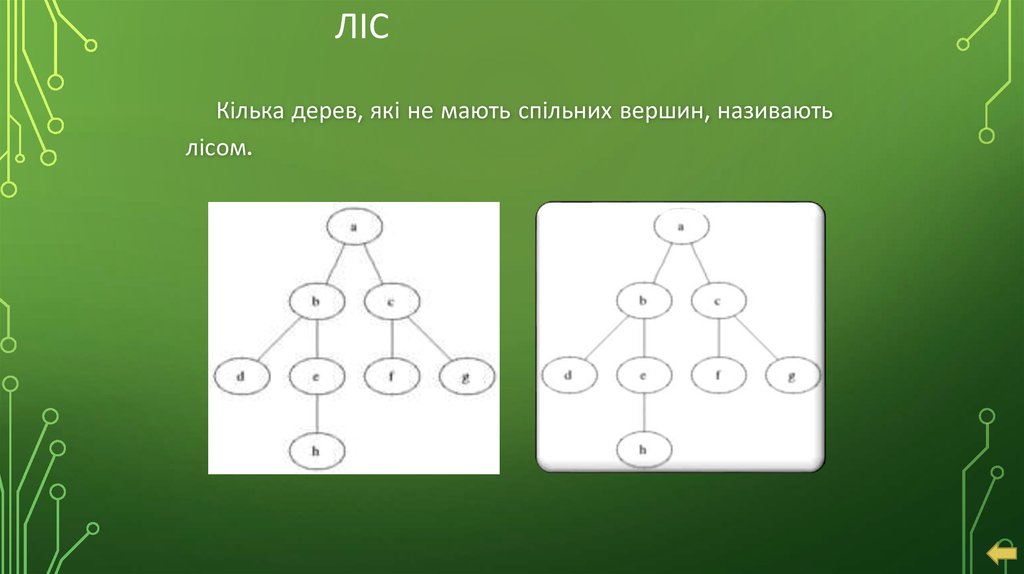
ЛІС
Кілька дерев, які не мають спільних вершин, називають
лісом.

14. Орієнтований граф

ОРІЄНТОВАНИЙ ГРАФ
Граф, у якому для всіх ребер
вказано напрям, називається
1
орієнтованим, або
орграфом.
В орієнтованому графі для
вершини 1 існує тільки два
орієнтовані цикли:
1) (1-2, 2-5, 5-3, 3-1),
2) (1-4, 4-7, 7-3, 3-1).
2
5
4
3
7
6

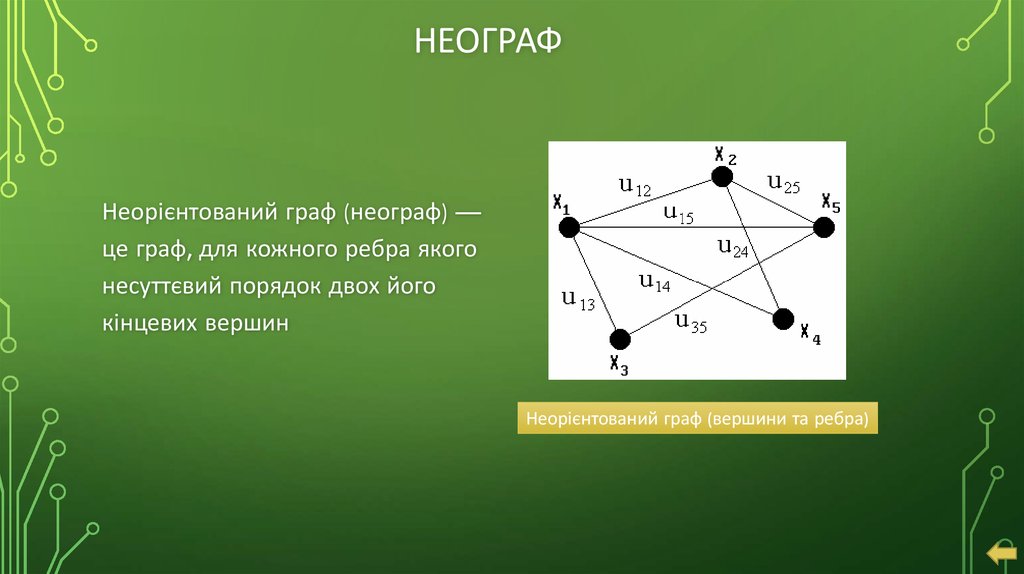
15. Неограф

НЕОГРАФ
Неорієнтований граф (неограф) —
це граф, для кожного ребра якого
несуттєвий порядок двох його
кінцевих вершин
Неорієнтований граф (вершини та ребра)

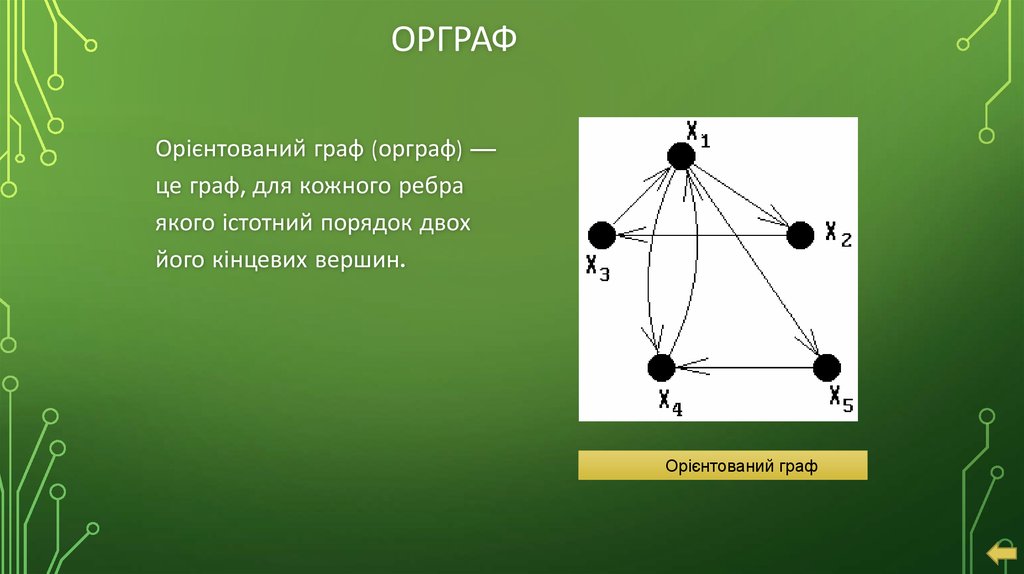
16. Орграф

ОРГРАФ
Орієнтований граф (орграф) —
це граф, для кожного ребра
якого істотний порядок двох
його кінцевих вершин.
Орієнтований граф

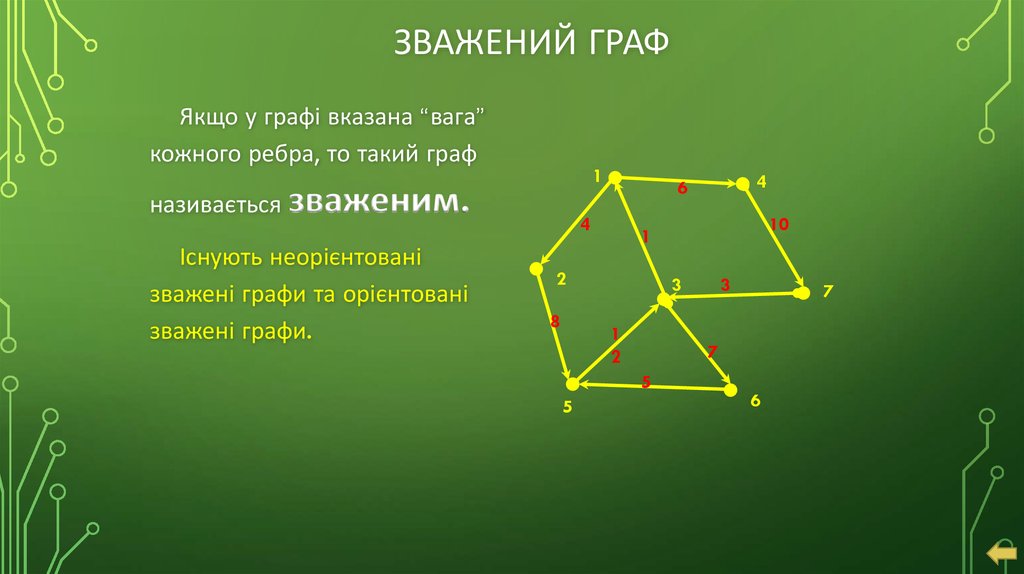
17. Зважений граф

ЗВАЖЕНИЙ ГРАФ
Якщо у графі вказана “вага”
кожного ребра, то такий граф
1
називається зваженим.
Існують неорієнтовані
зважені графи та орієнтовані
зважені графи.
4
3
1
2
3
7
7
5
5
10
1
2
8
4
6
6

18. Змішаний граф

ЗМІШАНИЙ ГРАФ
Змішаний граф – це граф, що
містить як орієнтовані, так і
неорієнтовані ребра. Кожен з
перерахованих видів графа може
містити одне або кілька ребер, у
яких обидва кінці сходяться в
одній вершині, такі ребра
називаються петлями.
Змішаний граф
Змішаний граф з петлями

19. Граф як геометрична конфігурація

ГРАФ ЯК ГЕОМЕТРИЧНА КОНФІГУРАЦІЯ
Наочно граф можна уявляти як
геометричну конфігурацію, яка
складається з точок (вершин
графу 1,2,3,4,5,6) і ребер (ліній
або відрізків №1(1-3), №2(34), №3(4-5), №4(3-5), №5(2-3),
№6(2-5), №7(5-6), №8(6-2),
№9(2-1), які сполучають деякі
точки (вершини) за вибраним
алгоритмом
Сутність геометричної конфігурації графа, в
якому всі вершини можна обійти за
маршрутом без перетинання ребер графу

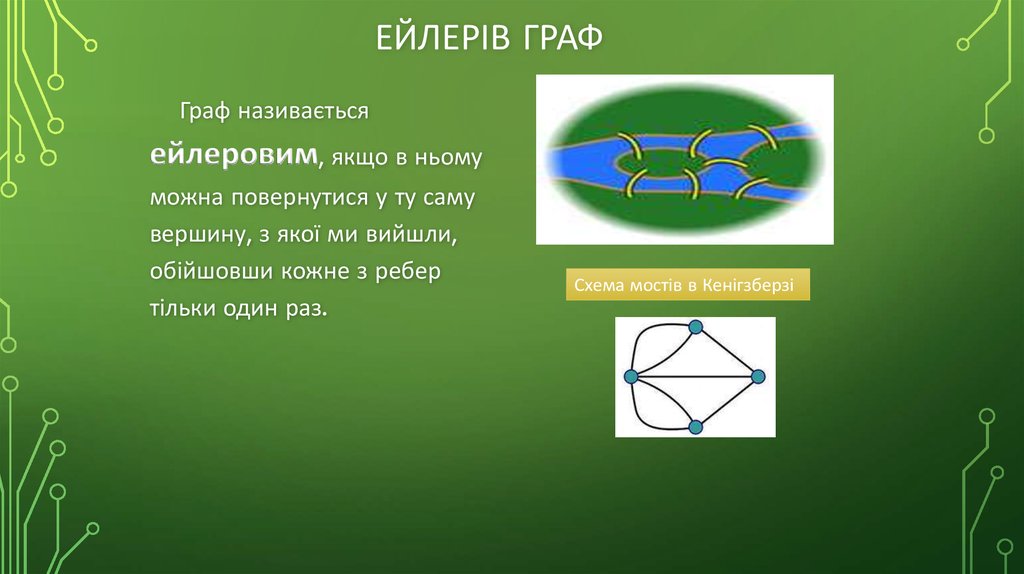
20. Ейлерів граф

ЕЙЛЕРІВ ГРАФ
Граф називається
ейлеровим, якщо в ньому
можна повернутися у ту саму
вершину, з якої ми вийшли,
обійшовши кожне з ребер
тільки один раз.
Схема мостів в Кенігзберзі

21.

Ойлер зауважив, що його граф не являє єдиного циклу: з
якої б вершини ми не почали б обхід, ми не можемо обійти
весь граф і повернутись назад, не проходячи жодного ребра
двічі. Якби такий цикл існував, то з кожної вершини
виходило б стільки ребер , скільки в неї входить , інакше
кажучи степінь кожної вершини була б парним числом.
Таким чином, відповідь на питання Ойлера - негативна.
Виклавши розв'язання задачі про кенігсберзькі мости,
Ойлер в своїй праці поставив питання: на яких графах
можна знайти цикл, який містить всі ребра графа, при чому
кожне ребро зустрічається в циклі рівно один раз?
Це дало початок системному математичному підходу до
побудови та вивчення властивості графів.

22. Зв'язний граф за Ойлером

ЗВ'ЯЗНИЙ ГРАФ ЗА ОЙЛЕРОМ
Зв’язний граф називається
ойлеровим графом, якщо існує
замкнений ланцюг, який
проходить через кожне ребро.
Такий ланцюг називають
ойлеровим ланцюгом, або
ойлеровим циклом
Структура вершин та ребер в
неорієнтованому ойлеровому графі (*
- означено точку входу ойлерового
ланцюга - циклу)