Similar presentations:
Основи теорії графів
1. «Основи теорії графів»
«ОСНОВИ ТЕОРІЇ ГРАФІВ»2. розділ математики, що дає змогу формалізувати взаємозв'язки між різноманітними видами інформації, організувати абстрактне їх
ТЕОРІЯ ГРАФІВРОЗДІЛ МАТЕМАТИКИ, ЩО ДАЄ ЗМОГУ ФОРМАЛІЗУВАТИ
ВЗАЄМОЗВ'ЯЗКИ МІЖ РІЗНОМАНІТНИМИ ВИДАМИ
ІНФОРМАЦІЇ, ОРГАНІЗУВАТИ АБСТРАКТНЕ ЇХ
ПРЕДСТАВЛЕННЯ.
3.
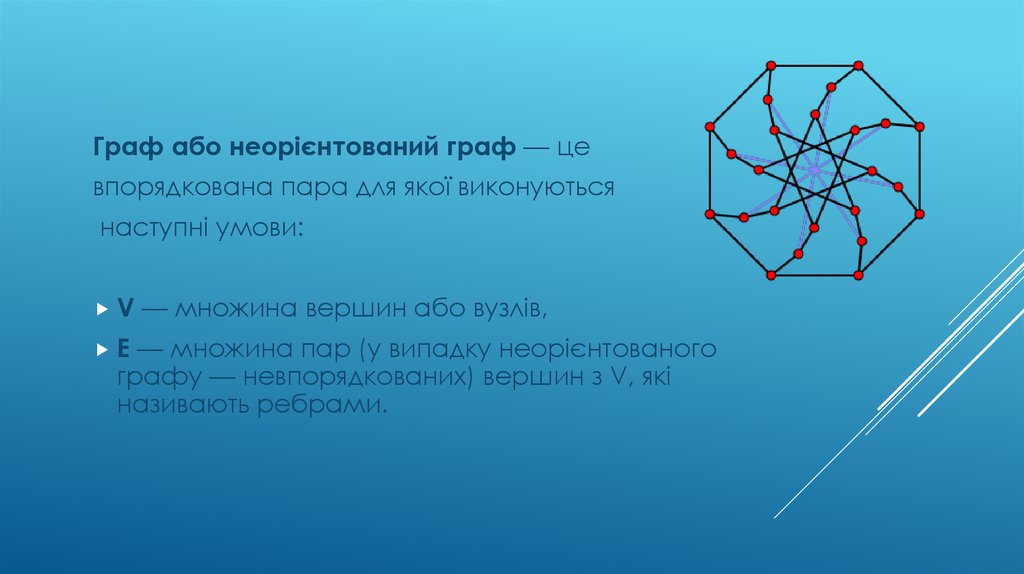
Граф або неорієнтований граф — цевпорядкована пара для якої виконуються
наступні умови:
V
E
— множина вершин або вузлів,
— множина пар (у випадку неорієнтованого
графу — невпорядкованих) вершин з V, які
називають ребрами.
4.
Якщоребро з'єднує дві вершини, то кажуть, що
воно інцидентне цим вершинам, а вершини, які
з'єднані таким ребром, називають суміжним.
5.
Петляв графі— ребро, інцидентне однієї і тієї ж
вершини. Строго кажучи, у петлі немає орієнтації.
Однак в орієнтованому графі для відмінності від
змішаного графа петлям надають орієнтацію.
6.
Вершини,які не належать кінцям жодного з ребер у
графі, називаються ізольованими.
Вершина А – приклад
ізольованої вершини.
7.
Граф,який складається лише з ізольованих
вершин, називається нуль-графом.
В
графі ребро без вершин існувати не може.
8.
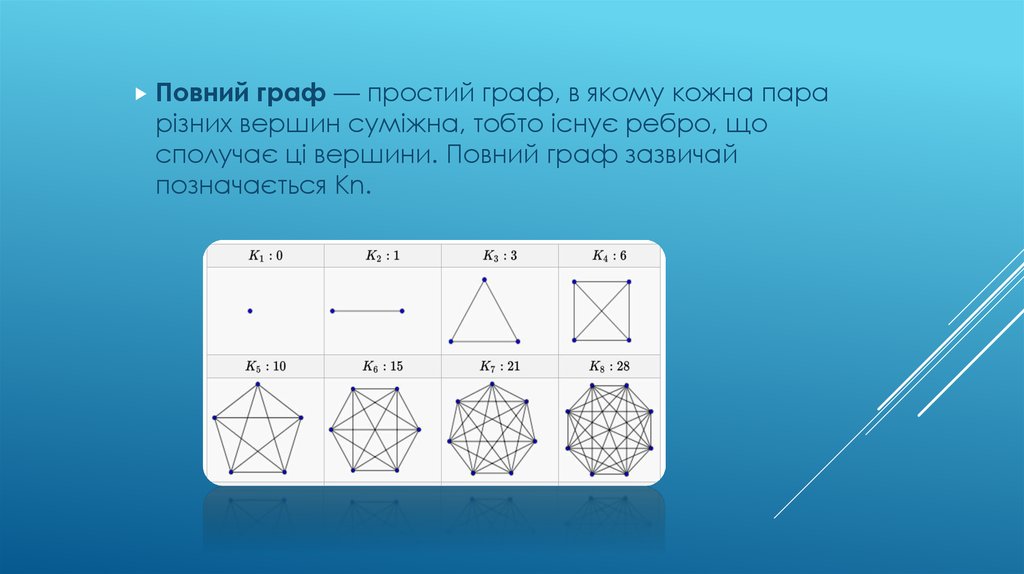
Повнийграф — простий граф, в якому кожна пара
різних вершин суміжна, тобто існує ребро, що
сполучає ці вершини. Повний граф зазвичай
позначається Kn.
9.
Якщовсі вершини і ребра графа знаходяться в
одній площині, то він називається плоским, у
протилежному випадку – просторовим.
10.
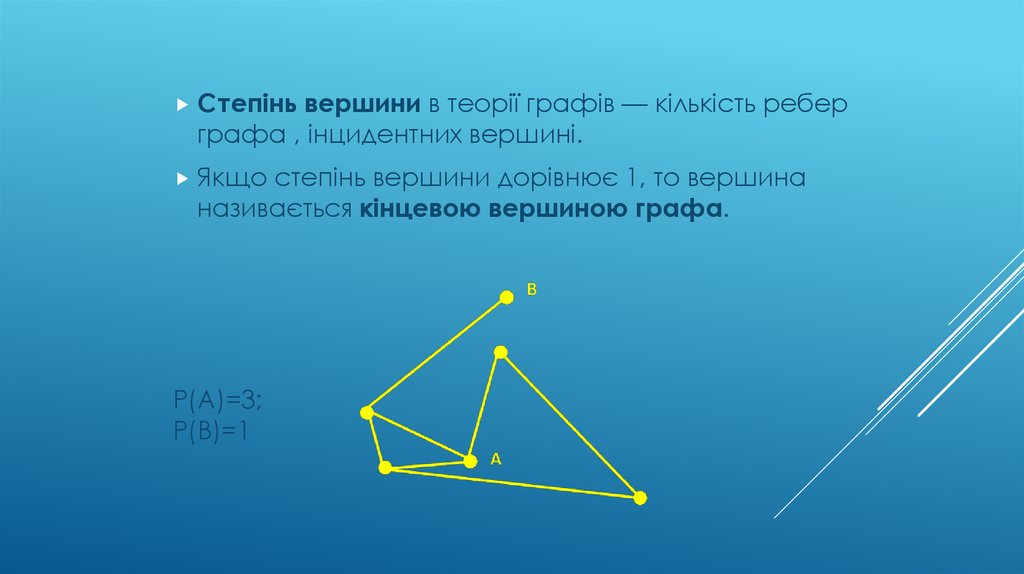
Степіньвершини в теорії графів — кількість ребер
графа , інцидентних вершині.
Якщо
степінь вершини дорівнює 1, то вершина
називається кінцевою вершиною графа.
Р(А)=3;
Р(В)=1
11. зв'язні вершини
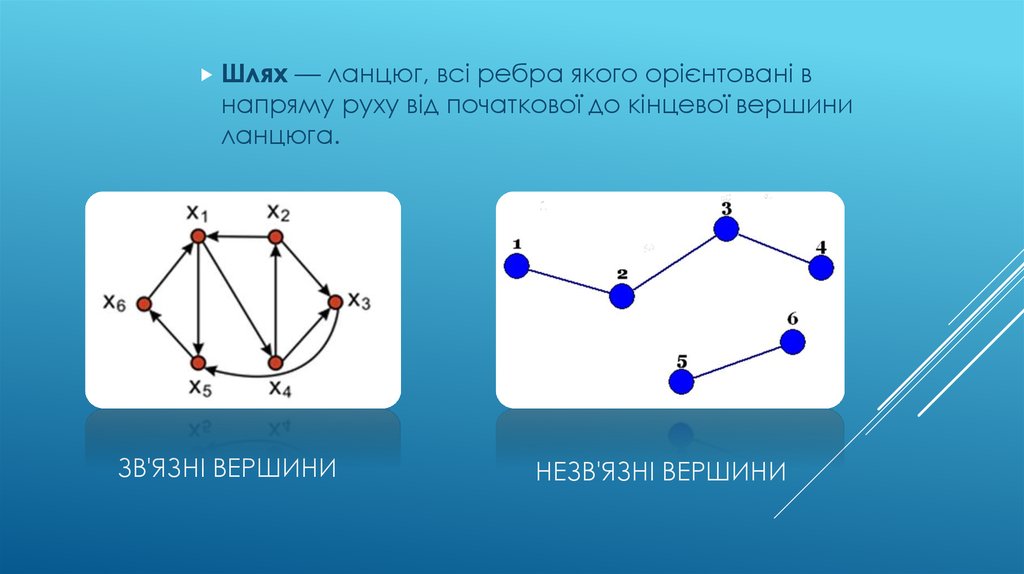
Шлях— ланцюг, всі ребра якого орієнтовані в
напряму руху від початкової до кінцевої вершини
ланцюга.
ЗВ'ЯЗНІ ВЕРШИНИ
НЕЗВ'ЯЗНІ ВЕРШИНИ
12.
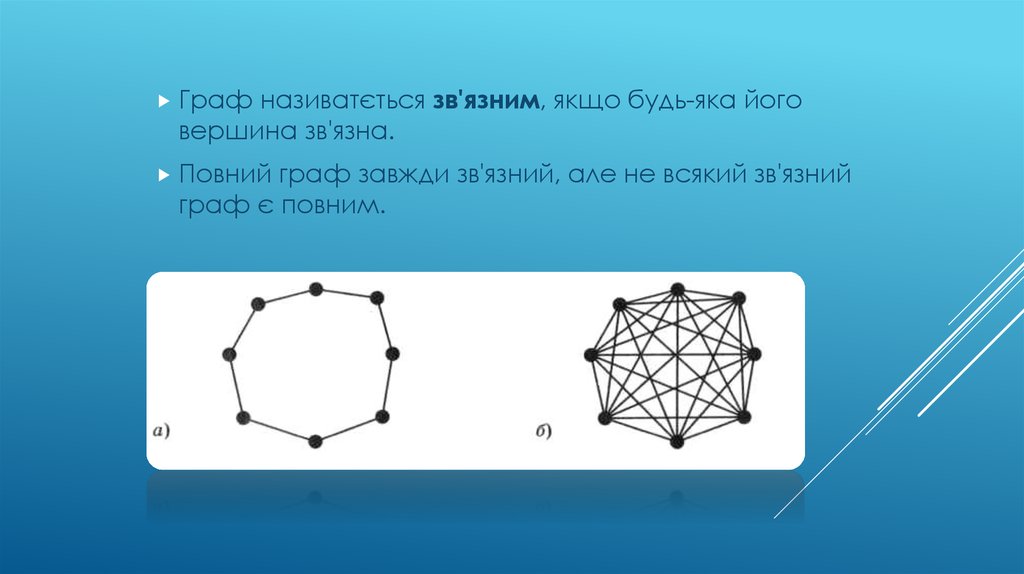
Графназиватється зв'язним, якщо будь-яка його
вершина зв'язна.
Повний
граф завжди зв'язний, але не всякий зв'язний
граф є повним.
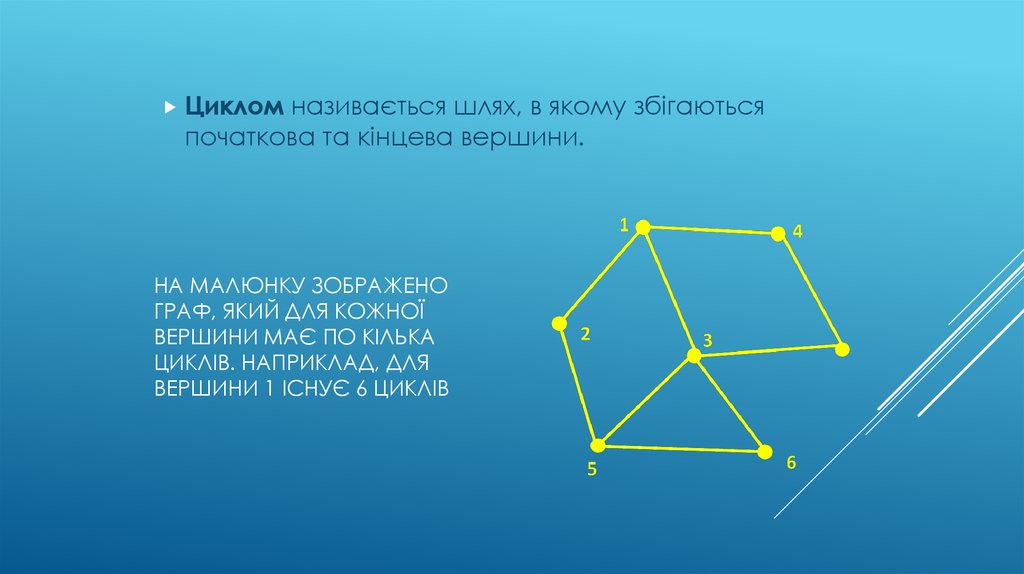
13. На малюнку зображено граф, який для кожної вершини має по кілька циклів. Наприклад, для вершини 1 існує 6 циклів
Цикломназивається шлях, в якому збігаються
початкова та кінцева вершини.
НА МАЛЮНКУ ЗОБРАЖЕНО
ГРАФ, ЯКИЙ ДЛЯ КОЖНОЇ
ВЕРШИНИ МАЄ ПО КІЛЬКА
ЦИКЛІВ. НАПРИКЛАД, ДЛЯ
ВЕРШИНИ 1 ІСНУЄ 6 ЦИКЛІВ
14. На малюнку для кожного вказаного циклу вершини 1 неважко порахувати довжину: 4, 4, 5, 5, 7, 7.
Довжиноюшляху (циклу) називається кількість
ребер цього шляху (циклу).
НА МАЛЮНКУ ДЛЯ КОЖНОГО
ВКАЗАНОГО ЦИКЛУ ВЕРШИНИ
1 НЕВАЖКО ПОРАХУВАТИ
ДОВЖИНУ: 4, 4, 5, 5, 7, 7.
15.
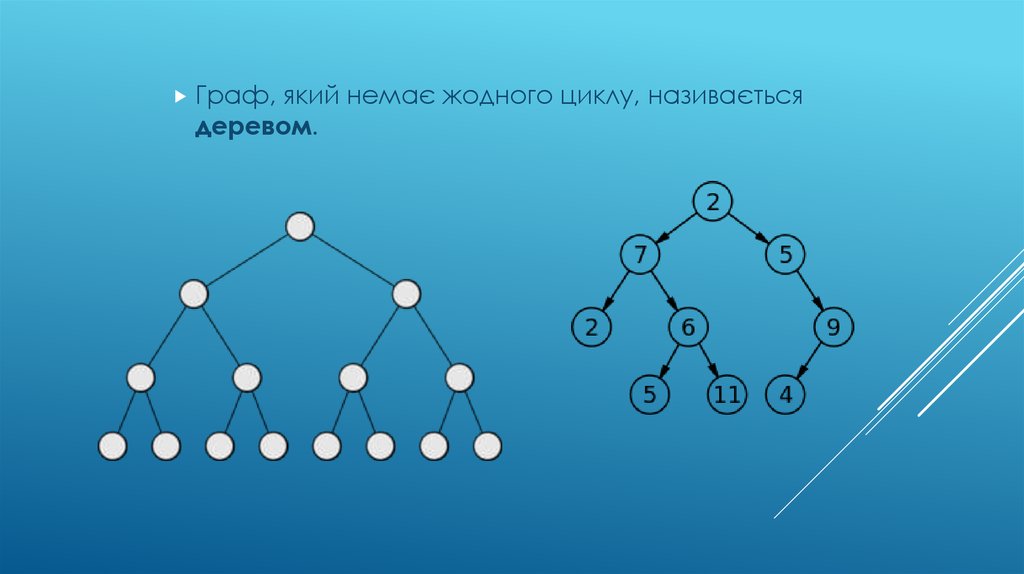
Граф,який немає жодного циклу, називається
деревом.
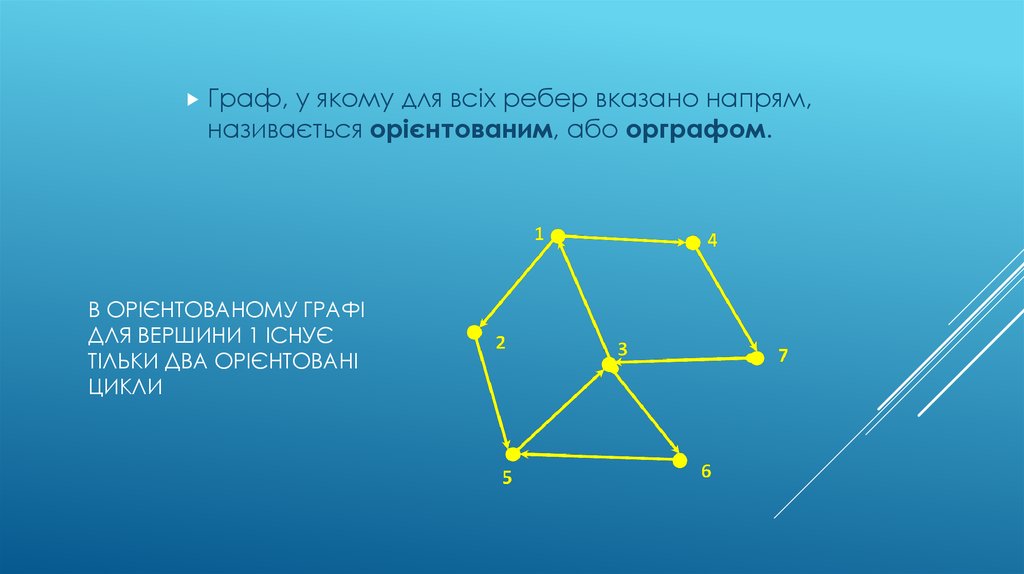
16. В орієнтованому графі для вершини 1 існує тільки два орієнтовані цикли
Граф,у якому для всіх ребер вказано напрям,
називається орієнтованим, або орграфом.
В ОРІЄНТОВАНОМУ ГРАФІ
ДЛЯ ВЕРШИНИ 1 ІСНУЄ
ТІЛЬКИ ДВА ОРІЄНТОВАНІ
ЦИКЛИ
17.
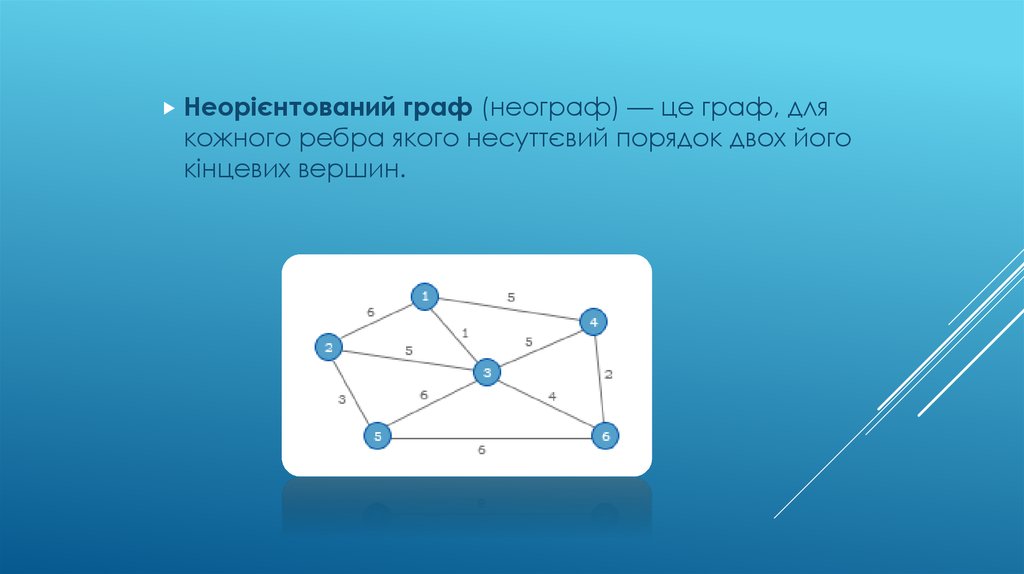
Неорієнтованийграф (неограф) — це граф, для
кожного ребра якого несуттєвий порядок двох його
кінцевих вершин.
18. Підграфи
ПІДГРАФИНехай задано граф G=(V,A). Граф G’=(V,A’), множина
вершин якого співпадає із множиною вершин графа G, а
множина ребер є підмножиною множини ребер графа
G, тобто,
A’
Нехай задано граф G=(V,A). Граф G’=(V’,A’), множина
вершин якого є підмножиною вершин графа G, тобто
V’ V а множина ребер є підмножиною множини ребер
графа G, тобто, A’ A, називається підграфом графа G.
A, називається частковим графом графа G.
19. Матриці, пов’язані з графами
МАТРИЦІ, ПОВ’ЯЗАНІ З ГРАФАМИНехай
задано граф G з вершинами {1,2,…,n}. Його
матрицею суміжності називається квадратна
матриця X розміру n x n, кожен елемент xij якої
дорівнює числу дуг з початком у вершині i та кінцем
у вершині j.
20. Матриця суміжності
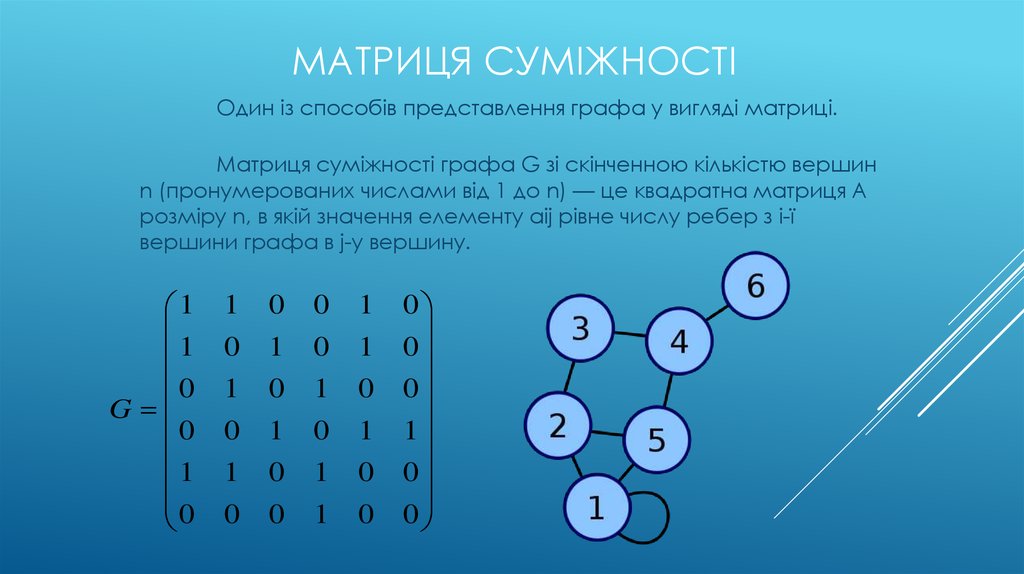
МАТРИЦЯ СУМІЖНОСТІОдин із способів представлення графа у вигляді матриці.
Матриця суміжності графа G зі скінченною кількістю вершин
n (пронумерованих числами від 1 до n) — це квадратна матриця A
розміру n, в якій значення елементу aij рівне числу ребер з i-ї
вершини графа в j-у вершину.
1
1
0
G
0
1
0
1
0
0
1
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
0
0
1
0
0
0
0
1
0
0
21. матриці інцидентності
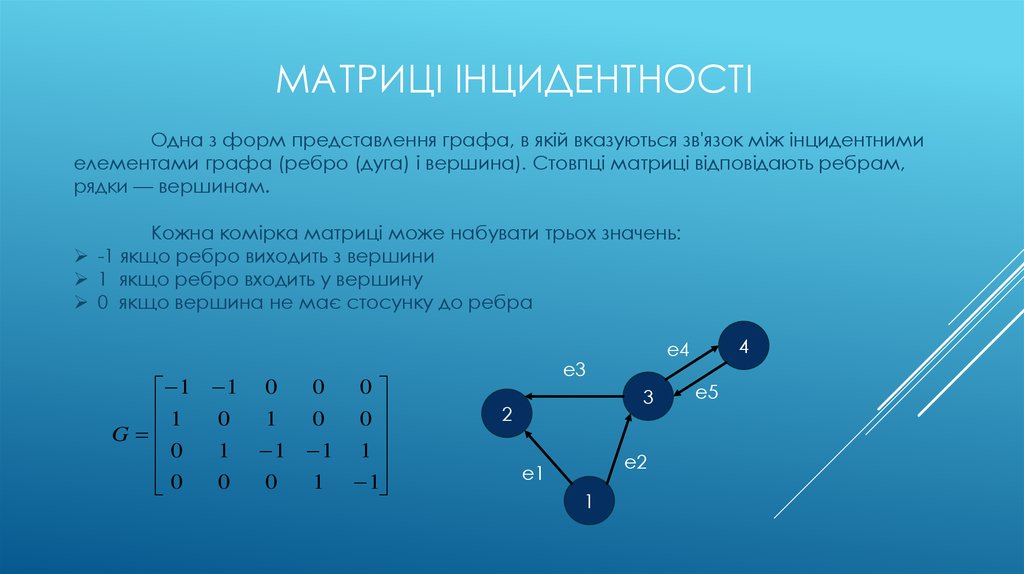
МАТРИЦІ ІНЦИДЕНТНОСТІОдна з форм представлення графа, в якій вказуються зв'язок між інцидентними
елементами графа (ребро (дуга) і вершина). Стовпці матриці відповідають ребрам,
рядки — вершинам.
Кожна комірка матриці може набувати трьох значень:
-1 якщо ребро виходить з вершини
1 якщо ребро входить у вершину
0 якщо вершина не має стосунку до ребра
0
0
1 1 0
1
0
1
0
0
G
0
1 1 1 1
0
0
0
1
1
e3
3
2
e2
e1
1
4
e4
e5
22.
Гамільтонівграф — в математиці це граф, що
містить гамільтонів цикл.
Гамільтонів
шлях — шлях, що містить кожну
вершину графа рівно один раз. Гамільтонів
шлях, початкова і кінцева вершини якого
збігаються, називається гамільтоновим циклом.
23.
Ейлерівланцюг або ейлерів шлях в
неорієнтованому графі це ланцюг, що проходить
кожне ребро рівно один раз.
Для
орієнтованих графів ланцюг заміняється на
шлях або орієнтованийй шлях і цикл на
орієнтований цикл.
24. Застосування теорії графів
ЗАСТОСУВАННЯ ТЕОРІЇ ГРАФІВВ хімії (для опису структур, шляхів складних реакцій);
комп'ютерна хімія — порівняно молода галузь хімії. Теорія
графів являє собою математичну основу хемоінформатика.
Теорія графів дозволяє точно визначити число теоретично
можливих ізомерів у вуглеводнів та інших органічних сполук.
В інформатиці та програмуванні .
У комунікаційних і транспортних системах. Зокрема, для
маршрутизації даних в Інтернеті.
В економіці.
В логістиці.
У схемотехніці (топологія з'єднання елементів на друкованій
платі або мікросхемі являє собою граф або гіперграф) .
25. Задача №1
ЗАДАЧА №1Дошка має форму подвійного хреста, який виходить, якщо з
квадрата 4x4 прибрати кутові клітини.
Чи можна обійти її ходом шахового коня і
повернутися на вихідну клітину, побувавши на
всіх клітинах рівно по одному разу?
Рішення:
Занумеруем послідовно клітини дошки:
А тепер за допомогою малюнка покажемо, що такий
обхід таблиці, як зазначено в умові, можливий:
1
9
3
2
7
8
5
6
11
10
4
12
1
2
3
4
5
6
7
8
9
10
11
12
26.
ЗАДАЧА №2З трьох осіб, що стоять поруч, один завжди говорить
правду (правдолюб), інший завжди бреше (брехун), а
третій, залежно від обставин, говорить або правду, або
неправду (дипломат).
Що стоїть зліва запитали: "Хто стоїть поруч з тобою?".
Він відповів: "Правдолюб".
Що стоїть в центрі поставили запитання: "Хто ти?",
І він відповів: "Я дипломат".
У того що стоїть праворуч запитали: "Хто стоїть поруч з
тобою?",
Він сказав: "Брехун".
Хто де стояв?
27.
Поруч зімною
правдолюб
Я
дипломат
Поруч зі
мною
брехун
Дипломат або бреше, або ні
Брехун завжди бреше
Правдолюб говорить тільки правду
28.
1Б
2
Д
Б
3
Д
Б
Д
П
29. Рішення
РІШЕННЯЯкщо в даній задачі ребро графа буде відповідати місцю,
займаному тією або іншою людиною, то нам можуть
представитися наступні можливості
Розглянемо першу можливість. Якщо "правдолюб" стоїть
зліва, то поруч з ним, судячи з його відповіді, також стоїть
"правдолюб". У нас же стоїть "брехун". Отже, ця
розстановка не задовольняє умові завдання. Розглянувши
таким чином всі інші можливості, ми прийдемо до
висновку, що позиція "дипломат", "брехун", "правдолюб"
задовольняє завданню. Дійсно, якщо "правдолюб" стоїть
праворуч, то, за його відповіді, поруч з ним стоїть "брехун",
що виконується. Що стоїть в центрі заявляє, що він
"дипломат", і, отже, бреше (що можливо з умови), а стоїть
праворуч також бреше. Таким чином, всі умови задачі
виконані
30. Задача №3
ЗАДАЧА №3Аркадій,
Борис, Володимир, Григорій і Дмитро при
зустрічі обмінялися рукостисканнями (кожен потиснув
руку кожному по 1 разу). Скільки всього рукостискань
було зроблено?
Б
В
А
Д
Г
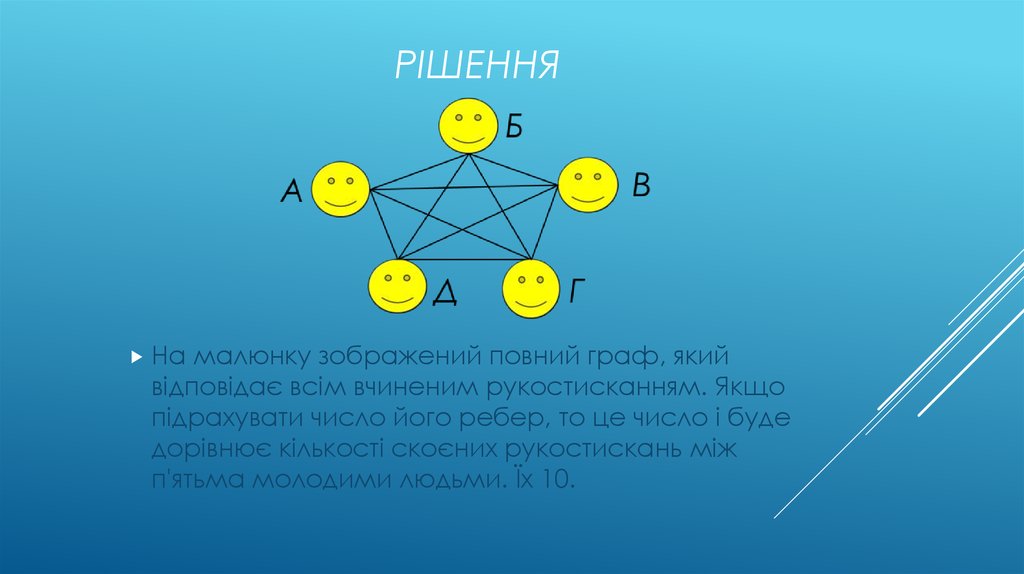
31. Рішення
РІШЕННЯНа
малюнку зображений повний граф, який
відповідає всім вчиненим рукостисканням. Якщо
підрахувати число його ребер, то це число і буде
дорівнює кількості скоєних рукостискань між
п'ятьма молодими людьми. Їх 10.
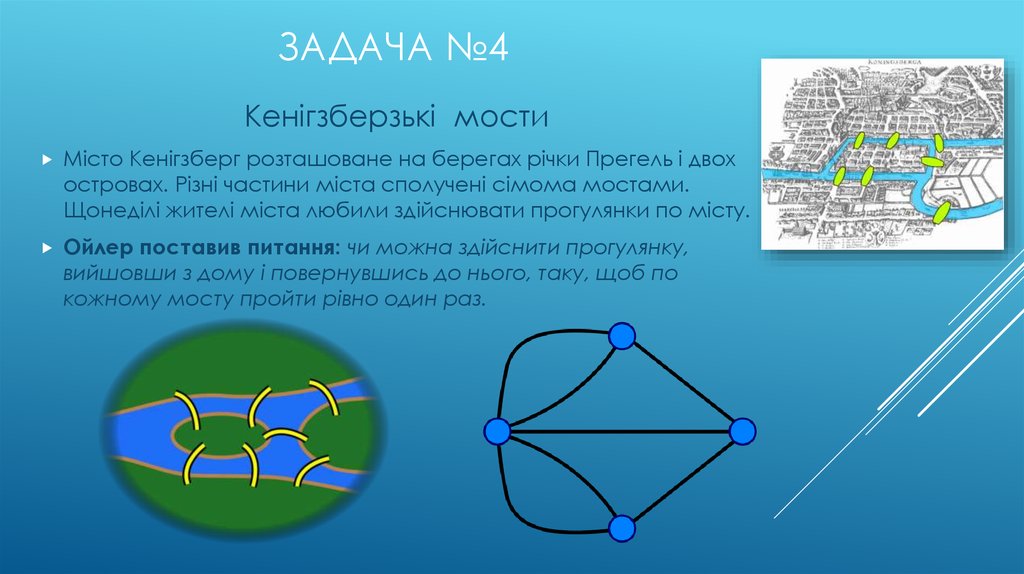
32. Задача №4
ЗАДАЧА №4Кенігзберзькі мости
Місто Кенігзберг розташоване на берегах річки Прегель і двох
островах. Різні частини міста сполучені сімома мостами.
Щонеділі жителі міста любили здійснювати прогулянки по місту.
Ойлер поставив питання: чи можна здійснити прогулянку,
вийшовши з дому і повернувшись до нього, таку, щоб по
кожному мосту пройти рівно один раз.
33. Ойлер зауважив, що його граф не являє єдиного циклу: з якої б вершини ми не почали б обхід, ми не можемо обійти весь граф і
ОЙЛЕР ЗАУВАЖИВ, ЩО ЙОГО ГРАФ НЕ ЯВЛЯЄЄДИНОГО ЦИКЛУ: З ЯКОЇ Б ВЕРШИНИ МИ НЕ ПОЧАЛИ Б
ОБХІД, МИ НЕ МОЖЕМО ОБІЙТИ ВЕСЬ ГРАФ І
ПОВЕРНУТИСЬ НАЗАД, НЕ ПРОХОДЯЧИ ЖОДНОГО
РЕБРА ДВІЧІ. ЯКБИ ТАКИЙ ЦИКЛ ІСНУВАВ, ТО З КОЖНОЇ
ВЕРШИНИ ВИХОДИЛО Б СТІЛЬКИ РЕБЕР , СКІЛЬКИ В НЕЇ
ВХОДИТЬ , ІНАКШЕ КАЖУЧИ СТЕПІНЬ КОЖНОЇ
ВЕРШИНИ БУЛА Б ПАРНИМ ЧИСЛОМ. ТАКИМ ЧИНОМ,
ВІДПОВІДЬ НА ПИТАННЯ ОЙЛЕРА - НЕГАТИВНА.




















 informatics
informatics