Оцінка складності алгоритмів та вибір ефективного алгоритму для вирішення задач різних типів

1.

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
УКРАЇНСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ НАУКИ ТА ТЕХНОЛОГІЙ
КАФЕДРА ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ І СИСТЕМ
Тема випускної роботи магістра:
«Оцінка складності алгоритмів та вибір ефективного
алгоритму для вирішення задач різних типів»
Керівник:
к.т.н., доц. А.О. Журба
Виконав:
Дніпро
2024
ст. гр. КН03-18-М
Павлюковець А. В.

2.

Постановка задачі
Мета роботи - дослідження та порівняння алгоритмів з метою вибору оптимального алгоритму для
розв'язання задач різних типів, що сприяє покращенню розуміння взаємозв'язку між характеристиками
алгоритмів та їх ефективністю у практичних застосуваннях.
Для досягнення мети роботи, необхідно вирішити наступні завдання:
1. Ознайомлення з основними поняттями та термінами, пов'язаними з оцінкою складності
алгоритмів.
2. Вивчення методів аналізу часової та просторової складності алгоритмів.
3. Освоєння прийомів порівняння ефективності різних алгоритмів для вирішення конкретних задач.
4. Визначення критеріїв вибору оптимального алгоритму та їх застосування у практиці.
5. Розгляд прикладів успішного використання ефективних алгоритмів у різних областях та проектах.
6. Аналіз та узагальнення отриманих знань для здатності ефективно вибирати алгоритми для
розв'язання різноманітних задач.

3.

Основні поняття
Алгоритм - це будь-яка правильно визначена обчислювальна процедура, на вхід (input) якої
подається певна величина або набір величин, і результатом виконання якої є вихідна (output) величина
або набір значень. Таким чином, алгоритм представляє собою послідовність обчислювальних кроків, які
перетворюють вхідні величини в вихідні
Емпіричний аналіз - це метод дослідження, який базується на зборі та інтерпретації фактичних
даних чи конкретних спостережень, а не на теоретичних розрахунках чи моделях.
Псевдокод - це спрощена, структурована мова програмування, яка використовується для опису
алгоритмів. Вона дозволяє нам позначити логіку алгоритму без прив'язки до конкретної мови
програмування та синтаксису.
Складність алгоритму визначається кількістю операцій чи обсягом пам'яті, які він вимагає для
вирішення завдання, та є ключовим фактором при виборі оптимального алгоритму.
Часова складність - кількість операцій чи кількість кроків, які виконує алгоритм, в залежності від
обсягу вхідних даних. Вимірюється у кількості операцій.
Просторова складність - обсяг пам'яті, яку алгоритм використовує для виконання завдання, в
залежності від розміру вхідних даних. Вимірюється у кількості використовуваних байтів чи структур
даних.
Біг-О нотація - математичний спосіб визначення верхньої межі часової або просторової складності
алгоритму( наприклад, O(n) вказує на лінійну складність).

4.

Сортування бульбашкою або сортування
обміном (Bubble Sort)
Сортування бульбашкою - це простий алгоритм сортування,
який отримав свою назву через спосіб, яким він працює. Цей
метод належить до класу алгоритмів обміну, оскільки він
порівнює та обмінює елементи масиву [1-8].
Алгоритм полягає в повторюваних проходах по масиву що
повинен бути відсортованим. За кожен прохід елементи
послідовно порівнюються попарно і, якщо порядок у парі
невірний, виконується обмін елементів. Проходи по масиву
повторюються до тих пір, поки на черговому проході не
виявиться, що обміни більше не потрібні, що означає - масив
відсортований. При проході алгоритму, елемент, що стоїть не на
своєму місці, «спливає» до потрібної позиції як бульбашка у
воді, звідси і назва алгоритму.

5.

Приклад реалізації алгоритму на Python та
його опис
1. Задається функція bubble_sort, яка приймає список arr
в якості аргументу.
2. Визначається змінна n, що представляє довжину
списку.
3. Вкладені цикли for використовуються для порівняння
та обміну елементів у списку. Зовнішній цикл
пройдеться по всіх елементах списку, а внутрішній
цикл буде виконуватися для кожного елемента до n - i
- 1, де i - номер поточної ітерації зовнішнього циклу.
4. Умова if arr[j] > arr[j + 1]: порівнює елементи у парі.
Якщо перший елемент більший за другий, то вони
обмінюються значеннями.
5. У функції __main__ створюється список my_list.
6. Виводиться початковий вигляд списку my_list.
7. Викликається функція bubble_sort для сортування
списку my_list.
8. Виводиться відсортований список my_list.

6.

Складність алгоритму
Складність алгоритму у найгіршому випадку рівна О(n²), де n — кількість
елементів для сортування. Існує чимало значно ефективніших алгоритмів,
наприклад, з найгіршою ефективністю рівною O(n log n).
Тому даний алгоритм має низьку ефективність у випадках, коли N є досить
великим, за винятком рідкісних конкретних випадків, коли заздалегідь відомо,
що масив з самого початку буде добре відсортований.

7.

Алгоритм Дейкстри (Dijkstra's Algorithm)
Алгоритм Дейкстри - це алгоритм пошуку найкоротших шляхів від одного з вузлів (початкового
вузла) до всіх інших вузлів у взваженому графі без циклів із від'ємними вагами. Алгоритм був
запропонований голландським вченим Едсгером Дейкстрою в 1956 році [1-8].
Алгоритм Дейкстри має просторову складність O(V + E), де V - кількість вузлів (вершин) у графі, а
E - кількість ребер. Основні елементи використовуваної пам'яті включають словники для збереження
відстаней та пріорітетної черги для обробки вузлів. Самі словники мають просторову складність O(V),
оскільки кожен вузол зберігається як ключ у словнику. Пріорітетна черга має просторову складність
O(V) у найгіршому випадку. Таким чином, загальна просторова складність алгоритму Дейкстри - O(V).
Треба врахувати, що у великих графах або графах з багатьма ребрами ця просторова складність
може виявитися значущою, тому завжди слід аналізувати вибір алгоритму в залежності від конкретних
вимог до швидкодії та ресурсів системи.

8.

Код алгоритма Дейкстри
Поетапне пояснення роботи коду
1. Ініціалізація:
- `distances` - словник, де ключі представляють
вершини графа, а значення - поточні відомі
найкоротші відстані від вихідної вершини (`start`).
На початковому етапі всі відстані встановлюються
на нескінченність, окрім вихідної вершини, у якої
відстань дорівнює 0.
- `priority_queue` - мін-куча, до якої додаються
пари `(відстань, вершина)`. Починаємо з вихідної
вершини.

9.

2. Цикл:
- Доки в `priority_queue` є елементи:
- Вилучаємо вершину з найменшою поточною відстанню від вихідної вершини
(`heappop`).
- Якщо поточна відстань більша, ніж відстань в `distances` для поточної вершини,
ігноруємо її (тому що ми вже знайшли коротший шлях до неї).
- Для кожного сусіда поточної вершини:
- Розраховуємо нову відстань від вихідної вершини до сусіда через поточну вершину.
- Якщо нова відстань менша за поточну відстань в `distances` для сусіда, оновлюємо її і
додаємо пару `(нова відстань, сусід)` в `priority_queue`.
3. Результат:
- Після завершення циклу отримуємо словник `distances` з найкоротшими відстанями від
вихідної вершини до всіх інших вершин.
У наданому коді використовується структура даних "мін-куча" (`heapq`), що забезпечує
ефективне вилучення вершини з мінімальною відстанню на кожному кроці. Це допомагає
зробити алгоритм Дейкстри більш ефективним.

10.

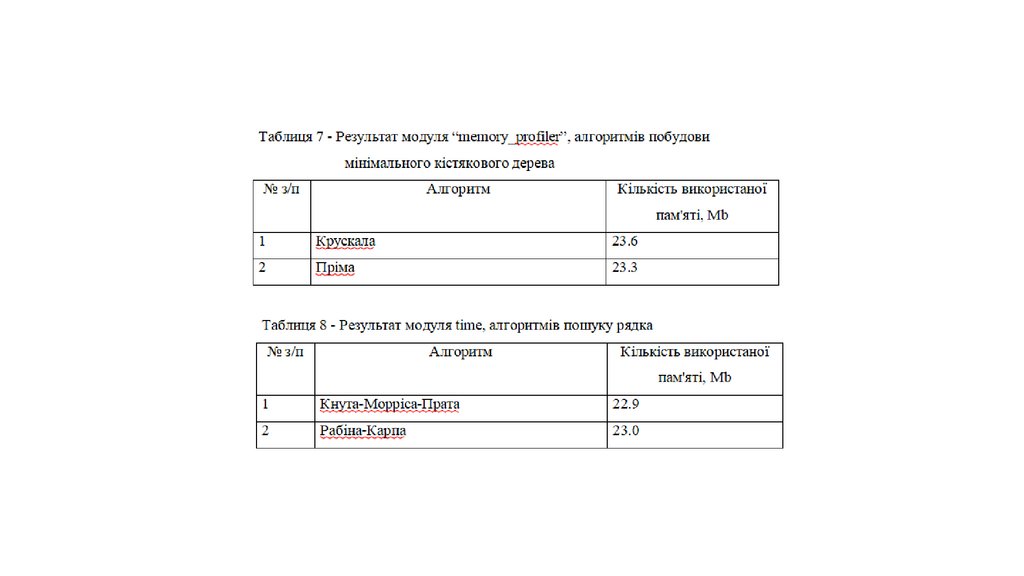
Модуль “time”та модуль
“memory_profiler”
Під час виконання алгоритмів за допомогою модуля time, вимірювався час виконання
кожного алгоритму для отримання об'єктивної інформації про їхню ефективність. Оскільки
алгоритми реалізовано, після підключення модуля, було зроблено заміри з одинаковою
довжиною масиву, та його елементами.
Модуль “memory_profiler” в Python призначений для вимірювання використання пам'яті
програмою в процесі виконання. Він надає інструменти для відстеження і аналізу, як пам'ять
виділяється та звільняється під час виконання програми.
Після виконання програми memory_profiler надасть подробовий звіт про те, як пам'ять
використовується в різних частинах вашого коду. Зокрема, він покаже пам'ять, виділену та
звільнену в кожній функції, а також загальний обсяг використаної пам'яті.
“Line #” - це номер рядка у вихідному коді.
“Mem usage” - це кількість використаної пам'яті на цьому етапі виконання програми.
“Increment” - це збільшення або зменшення використаної пам'яті порівняно з попереднім етапом.
“Line Contents” - це вміст рядка вихідного коду.

11.

Результати модулів, записані в таблиці

12.

13.

14.

15.

Детальне дослідження ефективності
елементарних алгоритмів сортування
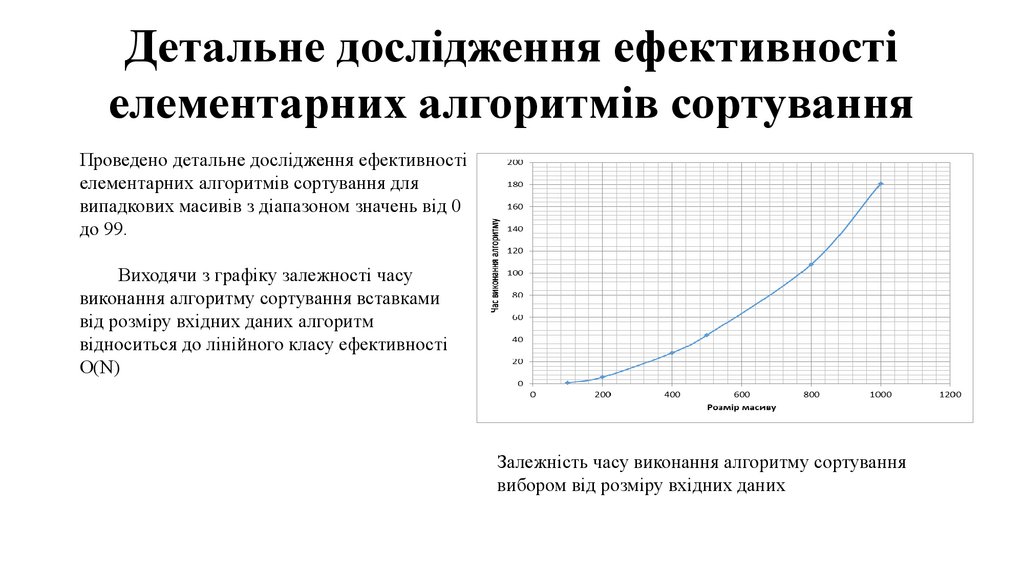
Проведено детальне дослідження ефективності
елементарних алгоритмів сортування для
випадкових масивів з діапазоном значень від 0
до 99.
Виходячи з графіку залежності часу
виконання алгоритму сортування вставками
від розміру вхідних даних алгоритм
відноситься до лінійного класу ефективності
О(N)
Залежність часу виконання алгоритму сортування
вибором від розміру вхідних даних

16.

Cортування вставками
Алгоритми сортування вибором та вставками
за часом виконання знаходяться у квадратичній
залежності від кількості елементів як для найгірших
так і для середніх випадків. Але при цьому вони не
потребують додаткової пам’яті. Таким чином, час їх
виконання відрізняється лише постійним
коефіцієнтом пропорційності цієї залежності, хоча
принципи роботи істотно відрізняються.
Сортування вставками показує хороші
результати при роботі з файлами, що не мають
вільну організацію. Сортування вставками на файлі,
що вже впорядкований, зводиться до того, що
з’ясовується, що всі елементи файлу знаходяться на
своїх місцях, а загальні витрати часу на сортування
лінійно залежать від кількості елементів. Але для
сортування вибором така залежність залишається
квадратичною.
Залежність часу виконання алгоритму
сортування вставками від розміру вхідних даних

17.

Порівняння результатів за кількістю операцій
для алгоритмів сортування вибором та
вставками для різних наборів вхідних даних
З результатів, наведених у таблиці, можна зробити висновок, що для алгоритму
сортування вставками та вибором значення елементів масивів вхідних даних
впливають на кількість операцій обміну та порівняння.

18.

Висновки
У даній кваліфікаційній роботі магістра було проведено ретельний аналіз швидкості алгоритмів та
розглянуто методи визначення найшвидших серед них. Дослідження включило в себе як
експериментальний, так і теоретичний аналіз, що дозволило отримати глибоке розуміння проблеми та
визначити ключові аспекти визначення швидкості алгоритмів.
В роботі проаналізовано алгоритми, написано їх програмну реалізацію та проведено їх емпіричний
аналіз та порівняння ефективності.
Крім того, отримані висновки відкривають перспективи для подальших досліджень у галузі
алгоритмічної оптимізації та розвитку нових методів аналізу швидкості. Відомості та інсайти, набуті у
цій роботі, можуть послужити основою для майбутніх досліджень, спрямованих на збільшення
ефективності обчислювальних процесів та вдосконалення алгоритмів для сучасних вимог
інформатизації.
Павлюковець А.В., Журба А.О. Оцінка складності алгоритмів та вибір ефектив-ного
алгоритму для вирішення задач різних типів // Молодь: наука та інновації: матеріали ХІ
Міжнародної науково-технічної конференції студентів, аспірантів та молодих вчених, Дніпро,
22–24 листопада 2023 року: у 2-х т. / Національний технічний університет «Дніпровська
політехніка» – Дніпро : НТУ «ДП», 2023. Том 2. С. 25-26.