Уравнение состояния идеального газа. Газовые законы

1. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА.ГАЗОВЫЕ ЗАКОНЫ

2. Актуализация опорных знаний

Что является объектом изучения
МКТ?
Что в МКТ называется
идеальным газом?
Какие три
термодинамических
параметра используют
для того, чтобы
описать состояние
идеального газа?
Идеальный газ.
Идеальный газ – это газ, в
котором взаимодействием между
молекулами можно пренебречь.
Давление, объем и температура.
Какое уравнение связывает между собой
все три термодинамических параметра?
Уравнение состояния
идеального газа.

3. НОВЫЕ ЗНАНИЯ

Изопроцессы – процессы,
протекающие при
неизменном значении
одного из параметров.
«Изо» - «постоянство».
Что называется изопроцессами?
Изобарный
Изохорный
Изотермический
Какие бывают изопроцессы?
Что называется
газовыми законами?
Количественная зависимость между
двумя макропараметрами при
неизменном значении третьего
Какое уравнение связывает между собой
все три термодинамических параметра?
Уравнение состояния
идеального газа.

4.

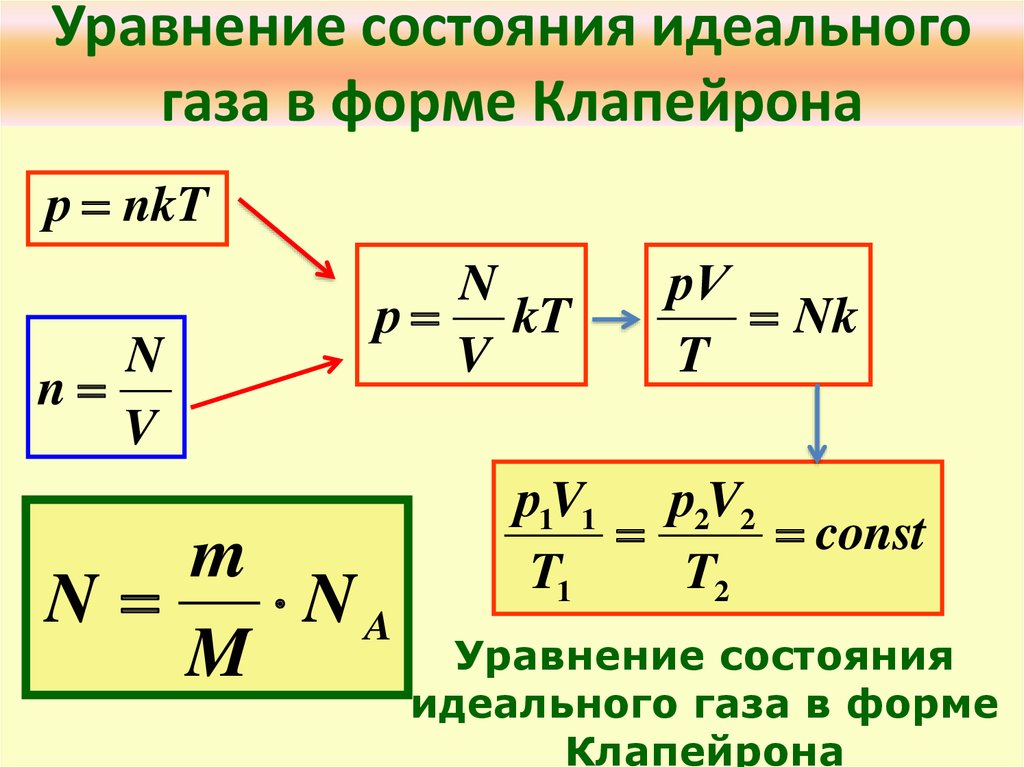
5. Уравнение состояния идеального газа в форме Клапейрона

р nkT
N
n
V
N
р kT
V
m
N
NA
M
рV
Nk
T
р1V1 р2V2
const
T1
T2
Уравнение состояния
идеального газа в форме
Клапейрона

6.

Менделеев Дмитрий Иванович
(8.II.1834–2.II.1907)
• Обобщив уравнение
Клапейрона,
в 1874 вывел общее
уравнение состояния
идеального газа

7.

Уравнение состояния идеального газа в форме
Менделеева- Клапейрона
р nkT
N
n
V
N
р kT
V
рV
Nk
T
m
N
NA
M
рV m
N Ak
T
M
Дж
1
Дж
23
R kN A 1,38 10
6,02 10
8,31
К
моль
моль К
R - универс. газ. постоянная
23
рV m
R
T
M
Уравнение состояния идеального
газа в форме
Менделеева- Клапейрона

8. Практическое применение уравнения состояния:

1. В термометрах…
• Уравнение позволяет
определить одну из
величин, характеризующих
состояние, если известны
две другие величины
• Это используют в
термометрах

9. 2. В газовых законах…

• Зная уравнение
состояния, можно
сказать, как протекают
в системе процессы
при определённых
внешних условиях

10. 3. В молекулярной физике…

• Зная уравнение
состояния, можно
определить, как
меняется состояние
системы, если она
совершает работу или
получает теплоту от
окружающих тел

11.

р1V1 р2V2
const
T1
T2
Df. Изотермический процесс-процесс изменения
состояния термодинамической системы
макроскопических тел при постоянной
температуре Т= const
Закон Бойля-Мариотта: р1V1 р2V2 рV соnst
Для газа данной массы произведение давления газа на
его объем постоянно, если температура газа не
соnst
меняется.
р
V
Э. Мариотт
Р. Бойль

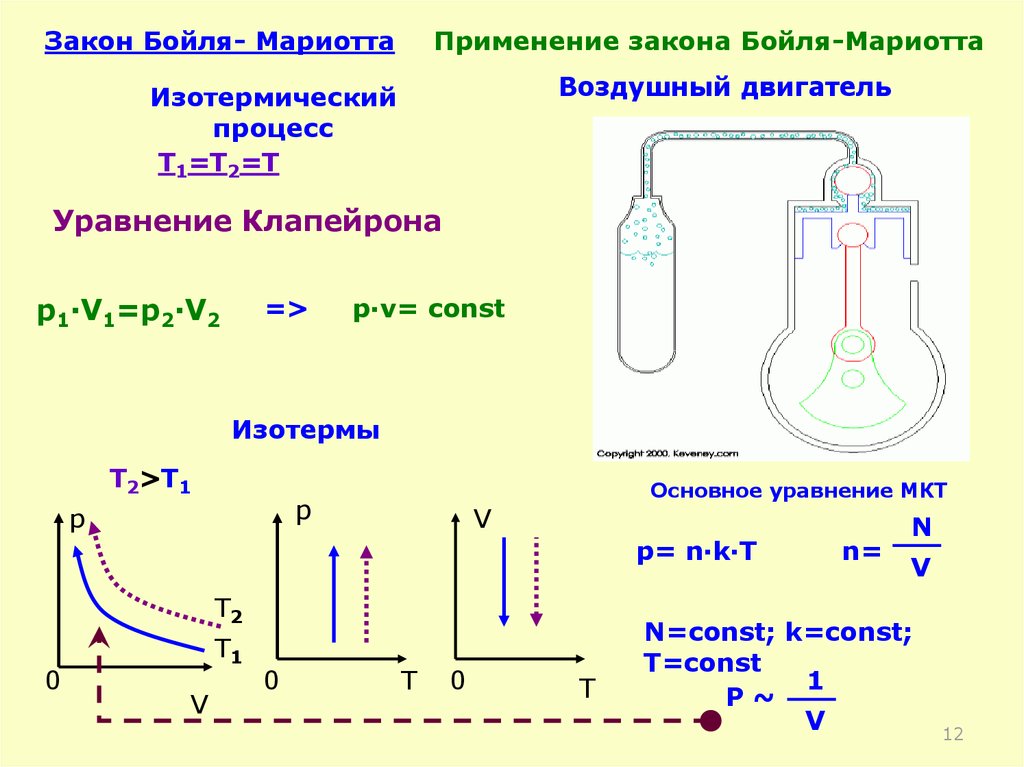
12.

Закон Бойля- Мариотта
Применение закона Бойля-Мариотта
Воздушный двигатель
Изотермический
процесс
T1=T2=T
Уравнение Клапейрона
p1·V1=p2·V2
=>
p·v= const
Изотермы
T2>T1
p
p
Основное уравнение МКТ
V
p= n·k·T
T2
0
T1
V
0
T
0
T
n=
N
V
N=const; k=const;
T=const
1
Р~
V
12

13.

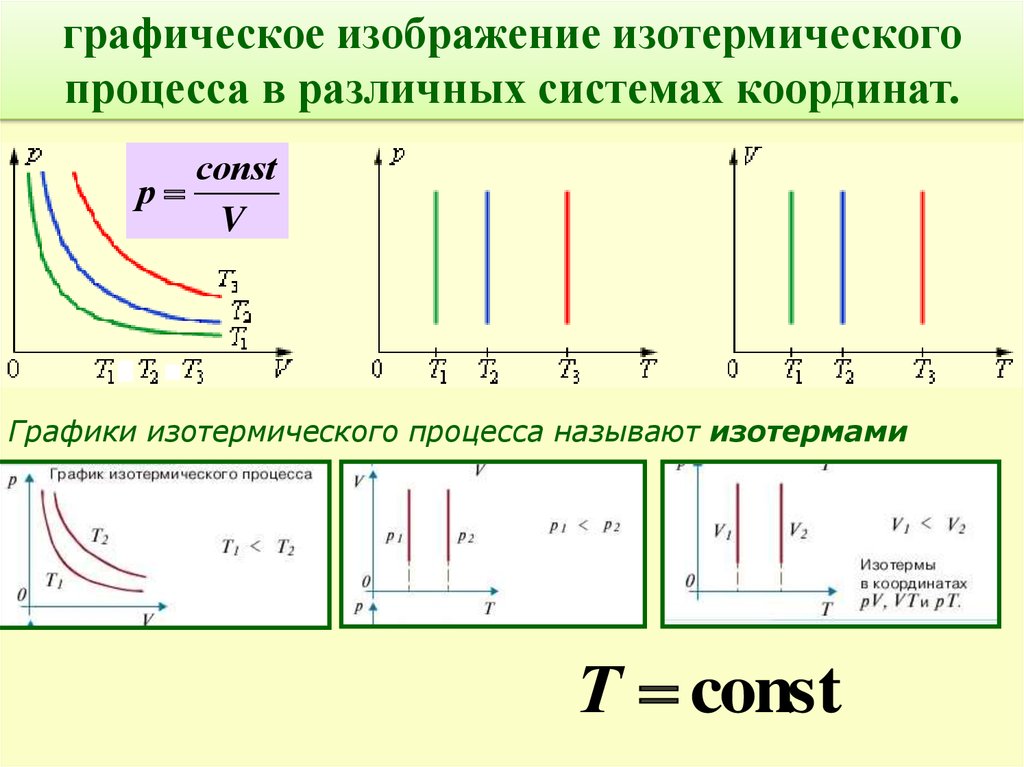
графическое изображение изотермического
процесса в различных системах координат.
соnst
р
V
Графики изотермического процесса называют изотермами
Т const

14.

р1V1 р2V2
const
T1
T2
Ж. Шарль
Изохорный процесс-процесс изменения
состояния термодинамической системы
макроскопических тел при постоянном объеме
V= const
Закон Шарля:
Для газа данной массы отношение давления газа к
температуре постоянно, если объем газа не меняется.
Df.
р1 р2
Т1 Т 2
р
const
Т
р Т соnst

15.

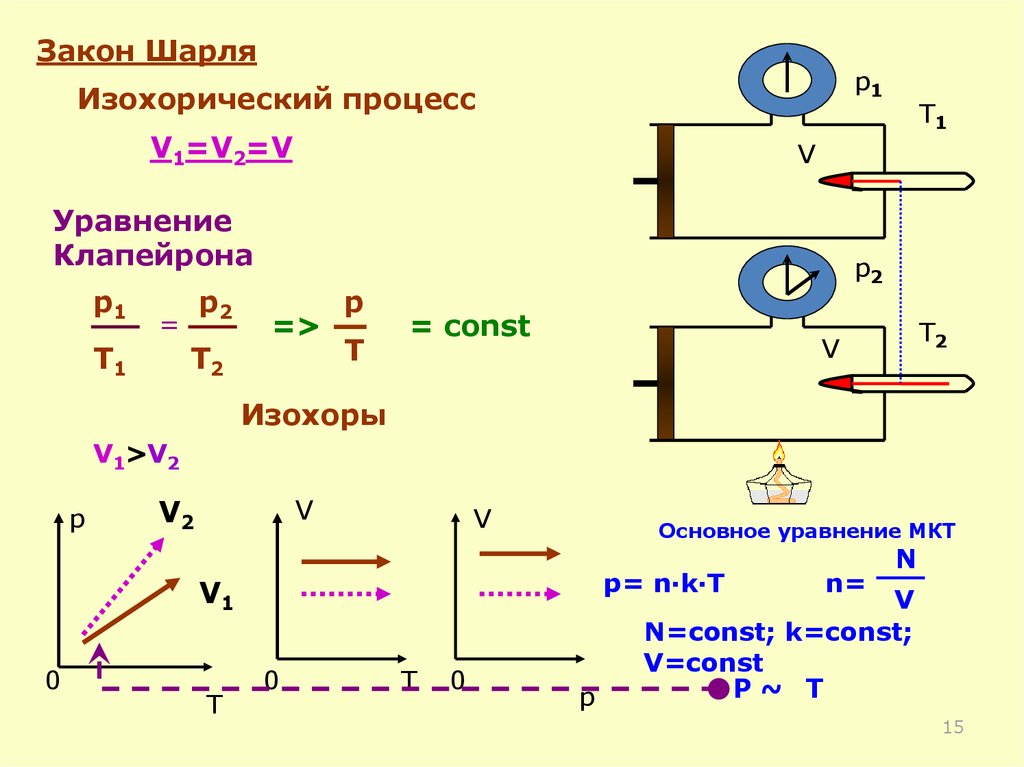
Закон Шарля
p1
Изохорический процесс
V1=V2=V
V
Уравнение
Клапейрона
p1
p2
=
T1
T2
T1
=>
p
T
p2
= const
T2
V
Изохоры
V1>V2
p
V2
V
V
Основное уравнение МКТ
p= n·k·T
V1
0
T
0
T
0
p
n=
N
V
N=const; k=const;
V=const
P~ T
15

16.

графическое изображение изохорного процесса
в различных системах координат.
V1<V2<V3
V= const
V1<V2<V3
р Т соnst
V1<V2<V3
V= const
Графики изохорного процесса называют изохорами.
р Т соnst

17.

р1V1 р2V2
const
T1
T2
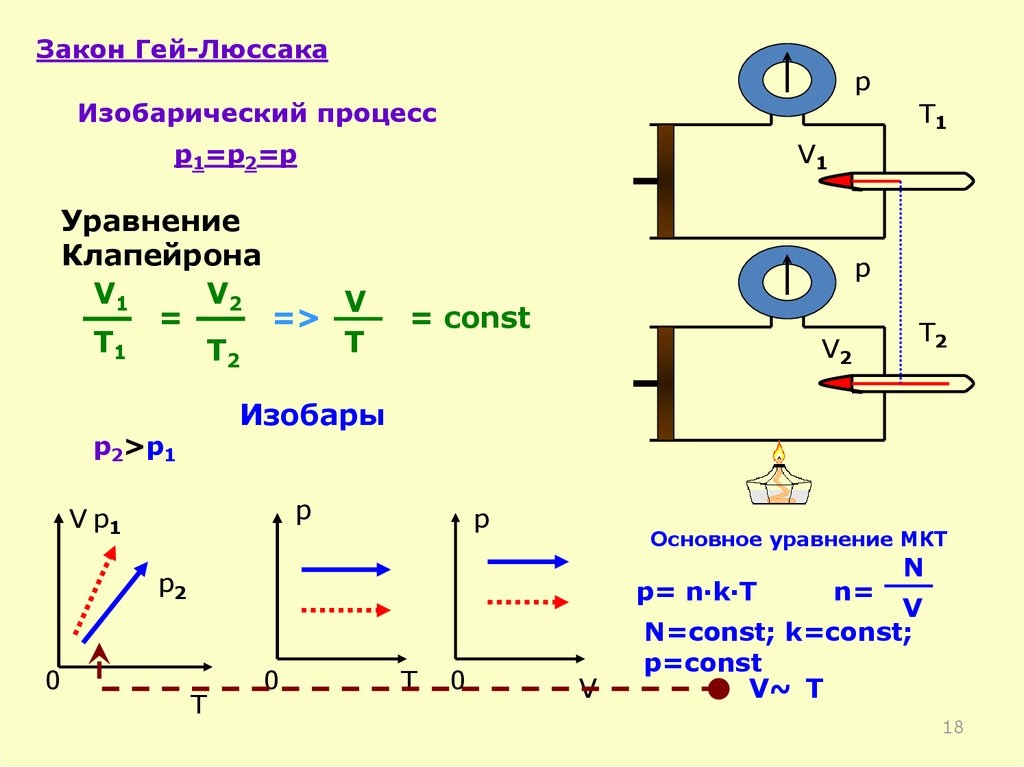
Df. Изобарный процесс-процесс изменения
состояния термодинамической системы
макроскопических тел при постоянном
давлении р= const
Закон Гей-Люссака:
Для газа данной массы отношение объема газа к
абсолютной температуре постоянно, если давление
газа не меняется.
V1 V2
T1 T2
V
соnst V T соnst
T
Ж. Гей-Люссак

18.

Закон Гей-Люссака
p
Изобарический процесс
T1
p1=p2=p
Уравнение
Клапейрона
V1
V2
V
=
=>
T1
T
T2
V1
p
= const
V2
Изобары
p2>p1
p
V p1
p
Основное уравнение МКТ
p2
0
T2
p= n·k·T
T
0
T
0
V
n=
N
V
N=const; k=const;
p=const
V~ T
18

19.

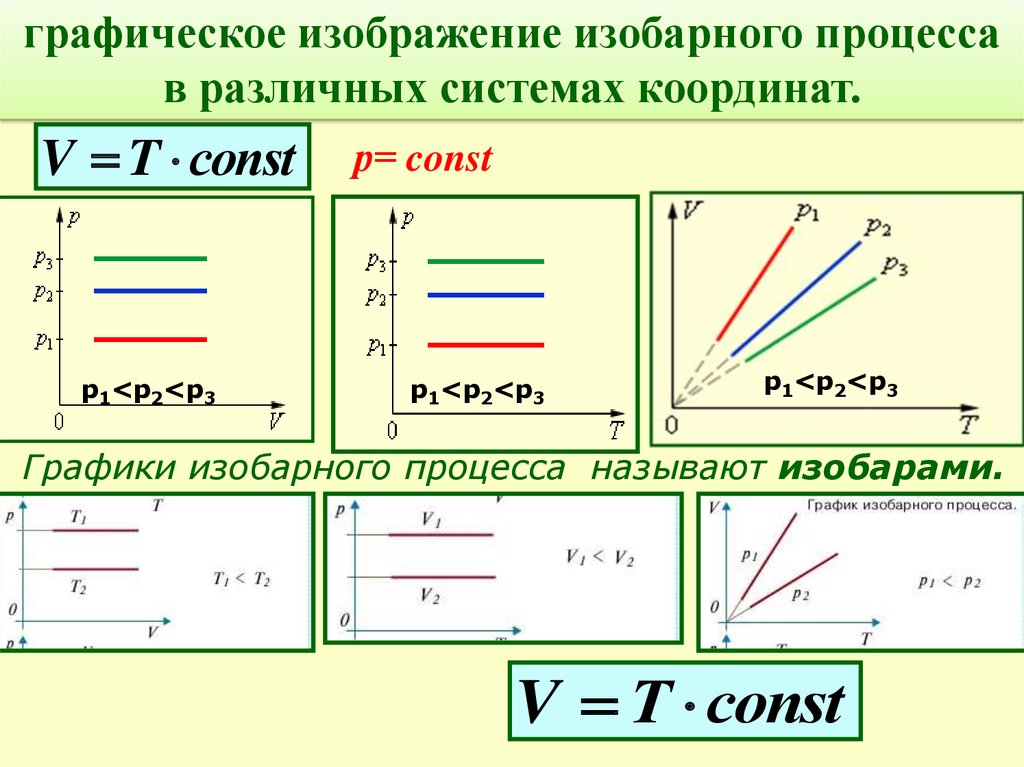
графическое изображение изобарного процесса
в различных системах координат.
V T соnst
р1<р2<р3
р= const
р1<р2<р3
р1<р2<р3
Графики изобарного процесса называют изобарами.
V Т соnst

20. Изопроцессы в газах

Процессы, протекающие при неизменном значении
одного из параметров, называют изопроцессами.
Название
процесса
Постоянная
величина
ИЗОПРОЦЕССЫ:
Изотермиче Изобарный Изохорный
ский
процесс
процесс
процесс
T = const
p = const
V = const

21. Обобщение

m
рV RT
M
m
ν
const
M
T = const
р1V1 = р2V2
T1
T2
V = const
р= const
р1V1 = р2V2
Бойля-Мариотта
V1
T1
=
V2
T2
Закон Гей-Люссака
р1
T1
=
р2
T2
Закон Шарля

22. Выполнение лабораторной работы.

Практическая часть
1. Инструктаж по ТБ.
2. Выполнение
практической
части работы по
инструкции
Аналитическая часть
1. Расчет искомых
величин.
2. Расчет
погрешностей.
3. Вывод о
проделанном
эксперименте.

23.

Опытная проверка
закона Гей – Люссака

24.

ХОД РАБОТЫ
• 1. Последовательность действий
• 2. Измерить ℓ в мм, t в ºС
• 3. С индексом (1) – горячее состояние,
(2) – холодное состояние
• 4. Измерить ℓ1 и ℓ2 , t1 и t2 – известны
• 5. Перевод t → Т

25.

ХОД РАБОТЫ
• 1. Последовательность действий
• 2. Измерить ℓ в мм, t в ºС
• 3. С индексом (1) – горячее состояние,
(2) – холодное состояние
• 4. Измерить ℓ1 и ℓ2 , t1 и t2 – известны
• 5. Перевод t → Т

26. Таблица результатов

27. Таблица результатов (продолжение)

28. Таблица результатов (продолжение)

29. Вычисления:

Т = t + 273
T1 = 64+273=327K T2 = 20+273 = 293K
1
500
1,17
2
426
Т1 327
1,15
Т2
293
Погрешности измерений:
Δℓ=Δℓи+Δℓо=1+0,5=1,5мм
ΔТ=ΔТи+ΔТо= 1+0,5 =1,5К
Относительные погрешности:
1,5 мм 1,5 мм
1
0,0065 0,65%
1 2 500 мм 425 мм
Т Т 1,5К
1,5К
2
0,0096 0,96%
Т1 Т 2 327 К 293К

30. Абсолютные погрешности:

1
1
1 1,17 0,0065 0,01
2
Т1
2 2 1,15 0,0096 0,01
Т2
1
1,16
1,18
2
1
1,17 0,01
2
Т1
1,15 0,01
Т2
Т1
1,14
1,16
Т2
Вывод: закон Гей- Люссака выполняется, так как
отношение объемов равно отношению температур
с учетом погрешностей

31. Домашнее задание.

1. Повторить теорию по теме «Молекулярно –
кинетическая теория. Идеальный газ. Уравнение
состояния. Основное уравнение МКТ. Газовые
законы».
2. Отчет о выполнении лабораторной работы.