Простейшие движения твердого тела

1. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
КИНЕМАТИКА
ЛЕКЦИЯ 2

2. ОПИСАНИЕ ДВИЖЕНИЯ ТЕЛА

Очевидно,
что если известен закон движения всех N точек тела, то
можно определить его положение и кинематические
характеристики всех составляющих его точек.
Вопрос:
можно ли это сделать, имея сведения о движении (зная
закон движения) лишь некоторой совокупности n<N точек
данного тела?
2
Кинематика тела

3. ОПИСАНИЕ ДВИЖЕНИЯ ТЕЛА

z
A2
A1
x
Покажем,
что
положение
твердого тела вполне определяется
заданием
6-и
независимых
параметров.
Возьмем 3-и не лежащие на
одной прямой точки тела A1, A2, A3
с координатами
A3
O
y
xk=xk(t), yk=yk(t), zk=zk(t) (k=1, 2, 3).
Их положение характеризуется 9-ю параметрами
(координатами).
3
Кинематика тела

4. ОПИСАНИЕ ДВИЖЕНИЯ ТЕЛА

Соединим точки между собой.
z
d1
A1
d3
x
O
Так как расстояния d1, d2, d3 не
изменяются, то координаты точек должны
удовлетворять уравнениям
A2
d 2 A4
( x2 x1 ) 2 ( y2 y1 ) 2 ( z2 z1 ) 2 d12
A3
y
( x3 x2 ) 2 ( y3 y2 ) 2 ( z3 z2 ) 2 d 22 (1)
( x1 x3 ) 2 ( y1 y3 ) 2 ( z1 z3 ) 2 d32
Следовательно из девяти координат независимых только
шесть, остальные три определяются из уравнений (1).
Если взять еще одну точку A4 с координатами x4, y 4, z 4,
то эти координаты должны будут удовлетворять трем
уравнениям вида (1).
4
Кинематика тела

5. ОПИСАНИЕ ДВИЖЕНИЯ ТЕЛА

Положение твердого тела относительно произвольно
выбранной системы координат вполне определяется 6-ю
независимыми параметрами.
Число
независимых
параметров,
определяющих
положение системы в пространстве называют числом
степеней свободы.
5
Кинематика тела

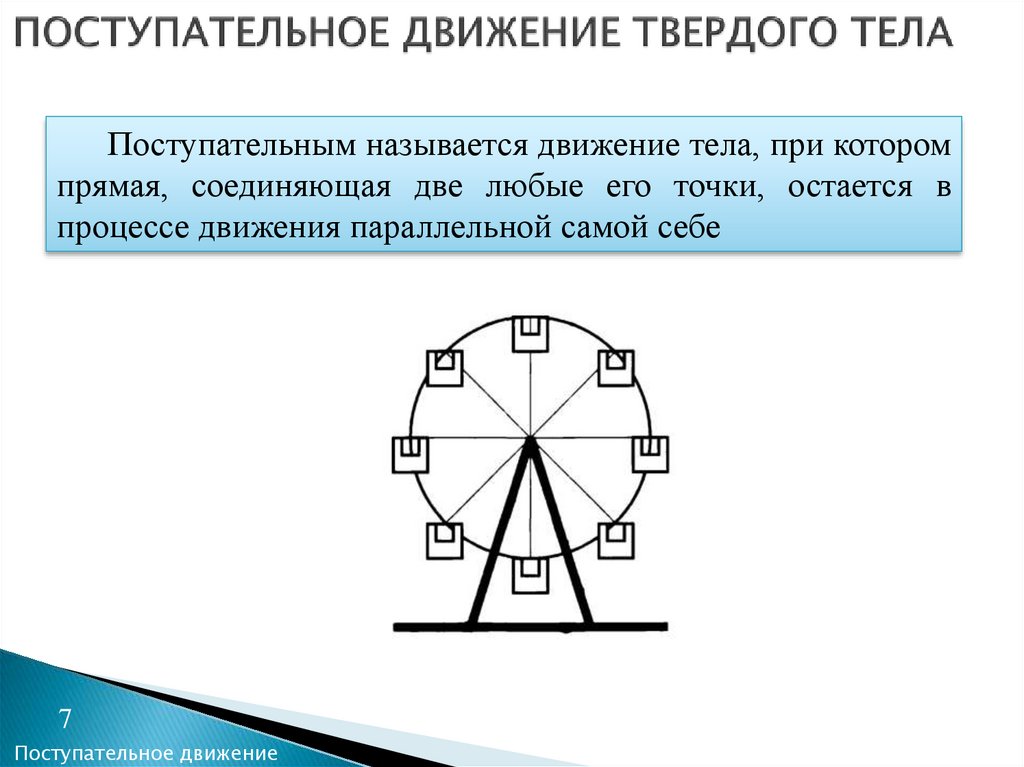
6. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

Поступательным называется движение тела, при котором
прямая, соединяющая две любые его точки, остается в
процессе движения параллельной самой себе
6
Поступательное движение

7. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

Поступательным называется движение тела, при котором
прямая, соединяющая две любые его точки, остается в
процессе движения параллельной самой себе
7
Поступательное движение

8. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

Теорема При поступательном движении тела все его
точки описывают одинаковые траектории и имеют в каждый
момент времени одинаковые скорости и ускорения
8
Поступательное движение

9. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

II
I
B0
z
rB
B
rA
A
A0
rA
rB
Доказательство.
Пусть твердое тело движется
поступательно относительно системы
координат Oxyz. Из рисунка следует
rB rA
(2)
В момент времени t тело занимало
положение I, а в момент t+ t положение II.
O
y
x
Во время движения вектор не изменяется,
A0B0 и AB равны и параллельны, A0B0BA – параллелограмм и
rA rB , т. е. перемещения всех точек равны между собой.
Продифференцировав (2) по времени, получим
drB drA d
.
dt
dt dt
9
Поступательное движение
(3)

10. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

d
0
,
то
Так как const
dt
или vB v A .
и
drB drA
dt
dt
(4)
Дифференцируя (4) устанавливаем связь между
ускорениями точек тела при поступательном движении
aB a A .
Теорема доказана
Поступательное движение тела полностью определяется
движением одной (любой) его точки.
Описание поступательного движения сводится к уже
изученной кинематике точки.
10
Поступательное движение

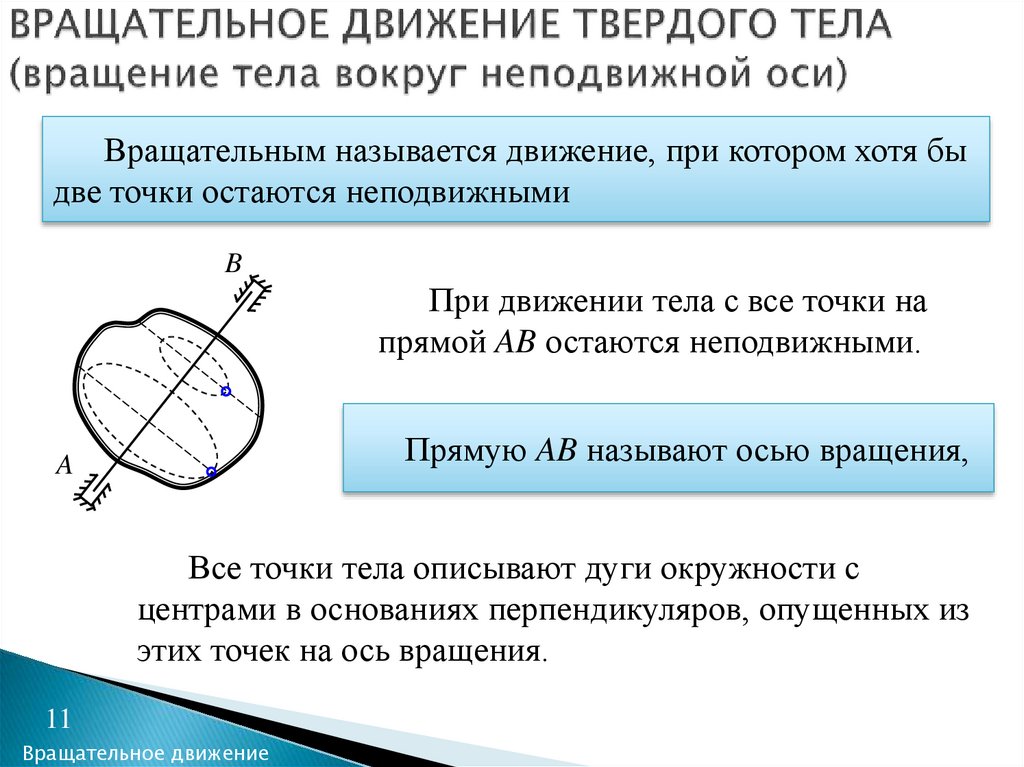
11. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА (вращение тела вокруг неподвижной оси)

Вращательным называется движение, при котором хотя бы
две точки остаются неподвижными
B
При движении тела с все точки на
прямой AB остаются неподвижными.
Прямую AB называют осью вращения,
A
Все точки тела описывают дуги окружности с
центрами в основаниях перпендикуляров, опущенных из
этих точек на ось вращения.
11
Вращательное движение

12. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

Возьмем на оси вращения две точки A и B
B
z
.
С
A
y
Так как положение точек A и B – известно,
то положение тела будет полностью
определено, если мы будем знать в любой
момент времени положение какой-либо не
лежащей на оси вращения точки C тела.
x
Из трех координат этой точки независимой будет только одна,
так как расстояния AC и BC постоянны
(xA-xC)2+(yA-yC)2 +(zA-zC)2 =AC2,
(xB-xC)2+(yB-yC)2 +(zB-zC)2 =BC2.
Положение тела, вращающегося вокруг
неподвижной оси, определяется одним параметром
12
Вращательное движение

13. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

z1
z
A
x
(t) x1
Направим ось
Az
неподвижной
системы координат Axyz вдоль оси
вращения тела.
Возьмем подвижную систему координат
Ax1y1 z1, жестко связанную с телом.
y1
(t) Положение тела будет полностью
y определено, если задан угол (t) между
неподвижной
Axz и подвижной Ax1z1
плоскостями.
(t) угол поворота тела
> 0 поворот против часовой стрелки, < 0 поворот по
часовой стрелки.
13
Вращательное движение

14. УГЛОВАЯ СКОРОСТЬ, УГЛОВОЕ УСКОРЕНИЕ

Угловой скоростью тела называется вектор, равный по
величине производной от угла поворота по времени и
направленый вдоль оси вращения в сторону, откуда вращение
видно проходящим против часовой стрелки
z
O1
d
Z
dt
Угловым ускорением называется вектор,
равный производной по времени от вектора
угловой скорости
O
d
dt
14
Вращательное движение

15. СКОРОСТИ ТОЧЕК ПРИ ВР. ДВИЖЕНИИ

z1
z
Положение произвольной точки
B
тела относительно неподвижной системы
координат определяется законом движения
rB rB (t ) xB (t ) i yB (t ) j z B (t ) k ,
B(t)
дифференцируя который по времени,
находим скорость точки B
vB rB x B (t ) i y B (t ) j
y
Чтобы определить x B и y B , рассмотрим
проекции радиус-вектора rB на оси Ox и Oy:
xB (t ) RB cos (t ) yB (t ) RB sin (t )
дифференцируя которые по времени, получим
B(0)
rB (0)
rB (t )
О
x
x1
О
yB
xB
RB
y
B
x
15
Вращательное движение
x B (t ) RB sin (t ) RB sin (t )
y B (t ) RB cos (t ) RB cos (t )

16. СКОРОСТИ ТОЧЕК ПРИ ВР. ДВИЖЕНИИ

vB RB sin i RB cos j ( yB i xB j ).
Полученное выражение для скорости можно записать в виде
vB RB rB ,
где RB - радиус-вектор вращения точки B в плоскости Oxy.
Действительно по определению векторного произведения
i
j k
i
j k
rB 0 0 RB 0 0 ( j xB i y B ).
xB y B z B
xB y B 0
Так как RB , то модуль скорости точки B
определяется так
vB RB ,
т.е. скорости точек вращающегося твердого тела
пропорциональны их расстояниям до оси вращения.
16
Вращательное движение

17. УСКОРЕНИЯ ТОЧЕК ПРИ ВР. ДВИЖЕНИИ

Продифференцируем выражение для скорости точки vB rB
по времени
d
d d
aB ( rB ) rB rB
dt
dt
dt
d
rB ( xB i y B j z B k ) rB ( x B i y B j )
dt
rB vB rB ( rB ).
z
Ускорение rB направлено по касательной
к траектории точки B и называется
aB v
B
вращательным ускорением
C
r
r
c
r aB rB (его модуль aB rB sin( , rB ) RB ).
B
aB
a
rB (t ) B
Вторая часть ускорения
c
aB vB ( rB )
О
y
направлена к оси вращения и по модулю равна
c
2
x
a B vB RB .
Это ускорение называется центростремительным.
17
Вращательное движение

18. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Положение какого количества точек твердого тела надо задать, чтобы описать
положение всего тела при произвольном движении?
2.Сколько степеней свободы у поступательно движущегося тела?
У вращающегося вокруг оси?
3. Куда направлены векторы угловой скорости и углового ускорения?
4. Какие кинематические характеристики одинаковы у двух точек твердого тела
при поступательном движении?
5. От чего зависит скорость точки тела при вращении вокруг оси?
6. Какое из двух ускорений (нормальное, тангенциальное) не может равно нулю
у точки вращающегося вокруг оси тела?
7. Можно ли утверждать, что траекторией точки поступательно движущегося
тела является примая?
18
НА СЛЕДУЮЩЕЙ ЛЕКЦИИ
ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА