Similar presentations:
Определенный интеграл
1. Определенный интеграл
Ащеулова Алена Сергеевна,кандидат физико-математических наук
2. Понятие определённого интеграла
x=ay
0 a
x=b
y = f(x)
b x
Криволинейная
трапеция- это фигура, ограниченная
графиком непрерывной неотрицательной функции f(x), x∈[a;b],
параллельными прямыми x=a и x=b и отрезком оси ОХ.
2
3. определённый интеграл
верхний предел интегрированияподынтегральная
подынтегральное
переменная
функция
выражение
интегрирования
b
f ( x) dx
a
нижний предел интегрирования
3
4. Свойства определённого интеграла
a1°
f ( x) dx 0
a
b
2°
k f ( x) dx k f ( x) dx ,
a
3°
b
k const
a
b
b
b
a
a
a
f ( x) g ( x) dx f ( x) dx g ( x) dx
4
5. Свойства определённого интеграла
4°b
a
a
b
f ( x) dx f ( x) dx
5 ° Если функция f(x) интегрируема на [a;b] и a<c<b, то
b
c
b
a
a
c
f ( x) dx f ( x) dx f ( x) dx
5
6. Формула Ньютона-Лейбница
bf ( x) dx F ( x) a F (b) F (a )
b
a
Исаак Ньютон
(25.12.1642 -20.03.1727)
знак двойной подстановки
Готфрид Вильгельм
Лейбниц
(21.06 (01.07) 1646 –
14.11.1716)
6
7. Вычислить интеграл
4 22
x
1. x dx
4
1
3
4
1
1
4
2 1
3
3
4
4 4
2. ( x 2 x)dx
3
4
4
1
4
4 4
x
x dx 2xdx
4
3
1
1
2 4
x
2
2
1
4 4
x
4
x
2 4
1
1
44 14
256 1
255
2
2
(4 1 )
(16 1)
15 78, 75
4
4
4 4
4
7
8.
88
2
x 3 x
3.
dx dx x 3 dx x
x
1
1
1
8
8
1
3 x
3
8
1
(8 1) 3( 3 8 3 1) 7 3(2 1) 4
4. sin x dx cos x
0
(cos cos 0) ( 1 1)
2
0
8
9. Метод замены переменной
t 2x2 12
1.
1
dt 2 x 2 1 ' 4 x dx
2 x dx
2
2
x
1
2
dx
dt
4
x 1 2 ( 1) 2 1 3
9
1
2dt
2
2t
4t
3
x 2 2 22 1 9
9
3
9
1
2t 3
1
1
1 1 1
2 3 2 9 6 18 9
Новые пределы интегрирования
9
10.
t x 1 x t 15
2. x x 1 dx
1
dt ( x 1) ' dx
x 1 1 1 0
x 5 5 1 4
2 54 2 3
t
t
0
5
3
4
0
4
(t 1) t dt
0
2 2 4 2
t t t t
0
5
3
4
0
4
3
2
4
1
2
t dt t dt
0
0
2
2
272
16 2 4 2
5
3
15
10
11. Метод интегрирования по частям
dxe
e
u ln x, du
e
dx
e
1. ln xdx
x ln x 1 dx
x x ln x 1 x
x
1
1
1
dv dx, v x
e
e ln e ln1 x 1 e e 1 1
e
11
12.
u ln xe
2. x ln x dx
1
2
dv x dx
2
dx
du
x
e
x
v
2
2
2 e
x
x
x
1
e
e
ln x 1
ln x 1 x dx
2
4
2
21
1
2
e
2
x
1
x
ln x 1e dx
2
21 x
2
e2
1
e 1
ln e ln1
2
2
4 4
e2 e2 1 1 e2
2 4 4
4
12







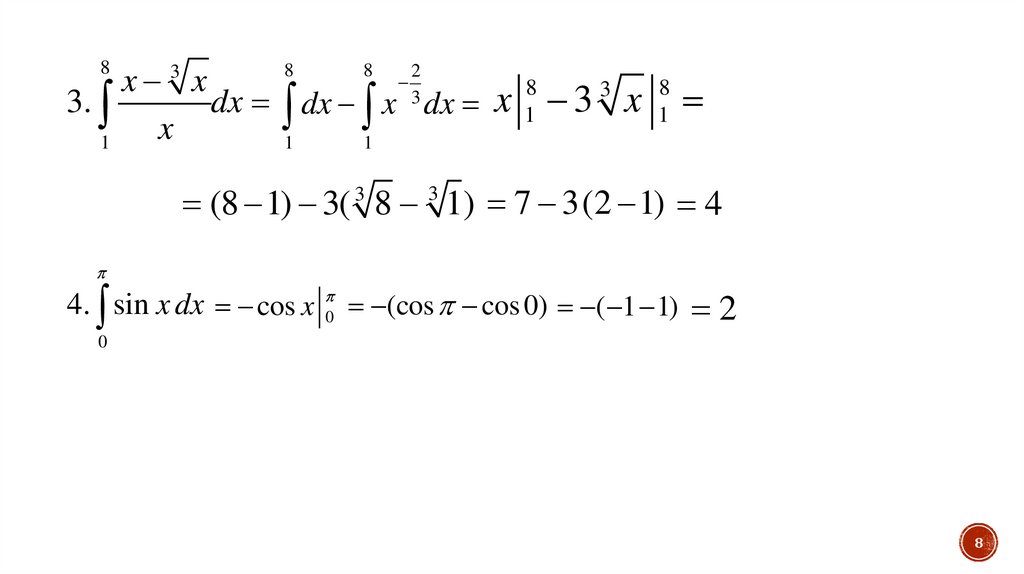

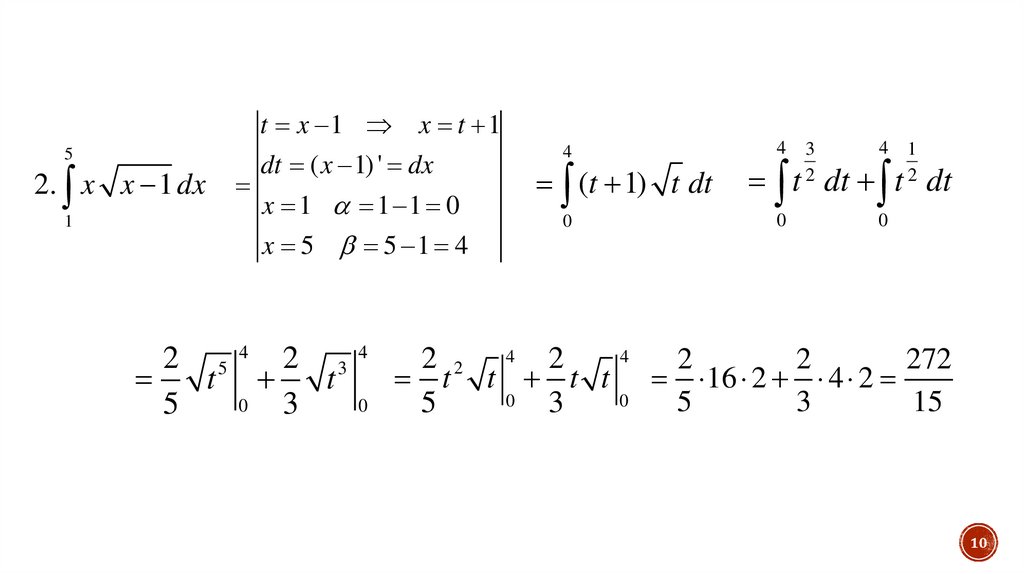
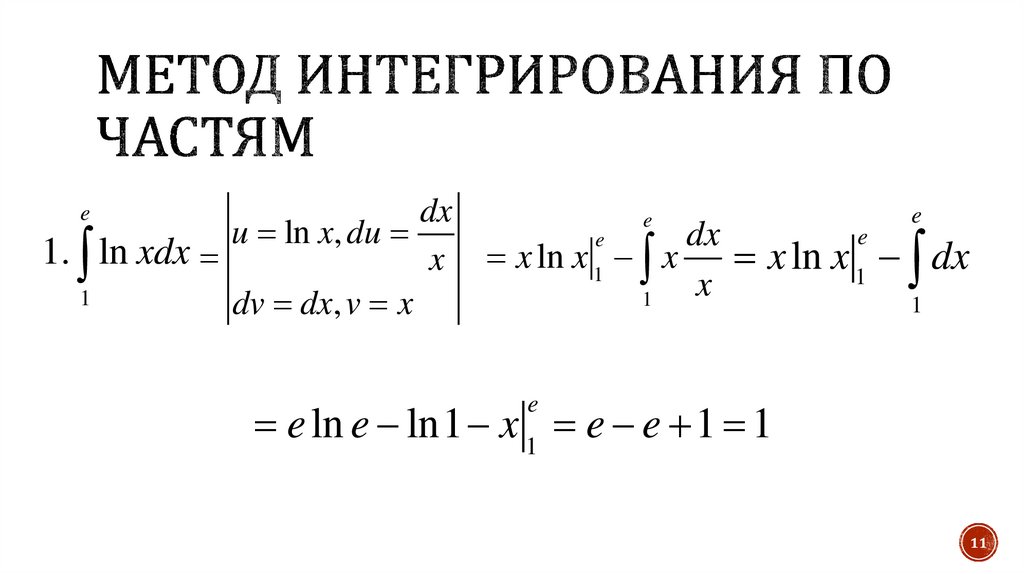
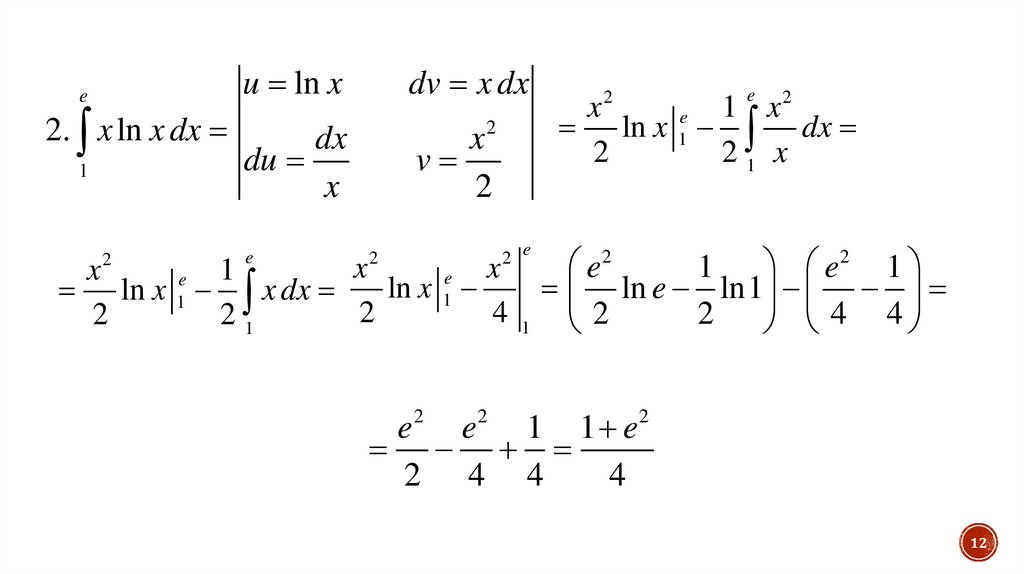
 mathematics
mathematics








