Дуга окружности

1.

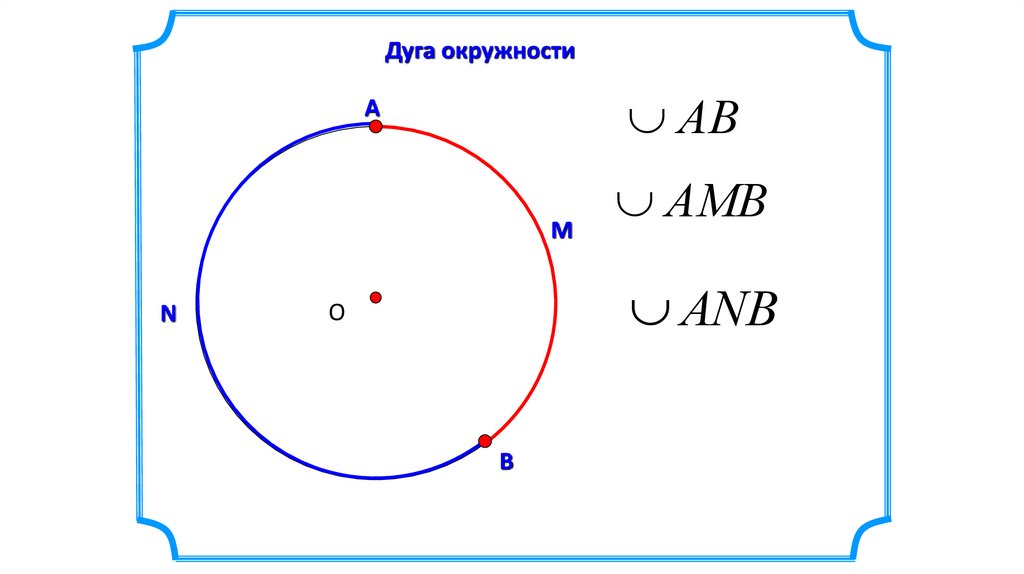
Дуга окружности
АВ
А
М
N
АМВ
АNВ
О
В

2.

Дуга называется полуокружностью, если отрезок,
соединяющий ее концы, является диаметром
окружности.
А
d
О
В

3.

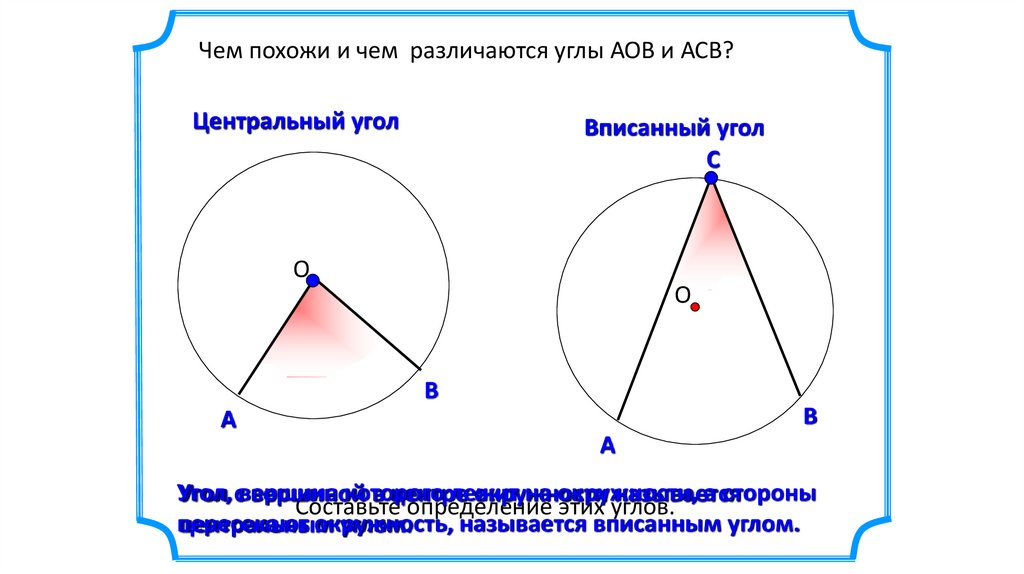
Чем похожи и чем различаются углы АОВ и АСВ?
Центральный угол
Вписанный угол
С
О
О
В
А
В
А
Угол,
которого
лежит
на окружности,
а стороны
Угол свершина
вершиной
в центре
окружности
называется
Составьте определение этих углов.
пересекают
окружность,
называется вписанным углом.
центральным
углом.

4.

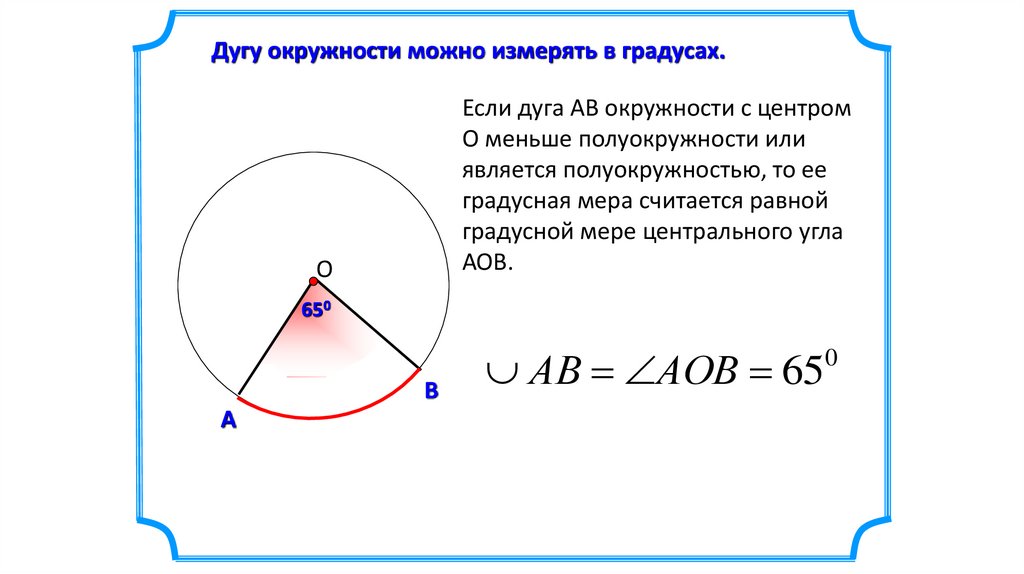
Дугу окружности можно измерять в градусах.
Если дуга АВ окружности с центром
О меньше полуокружности или
является полуокружностью, то ее
градусная мера считается равной
градусной мере центрального угла
АОВ.
О
650
В
А
АВ АОВ 65
0

5.

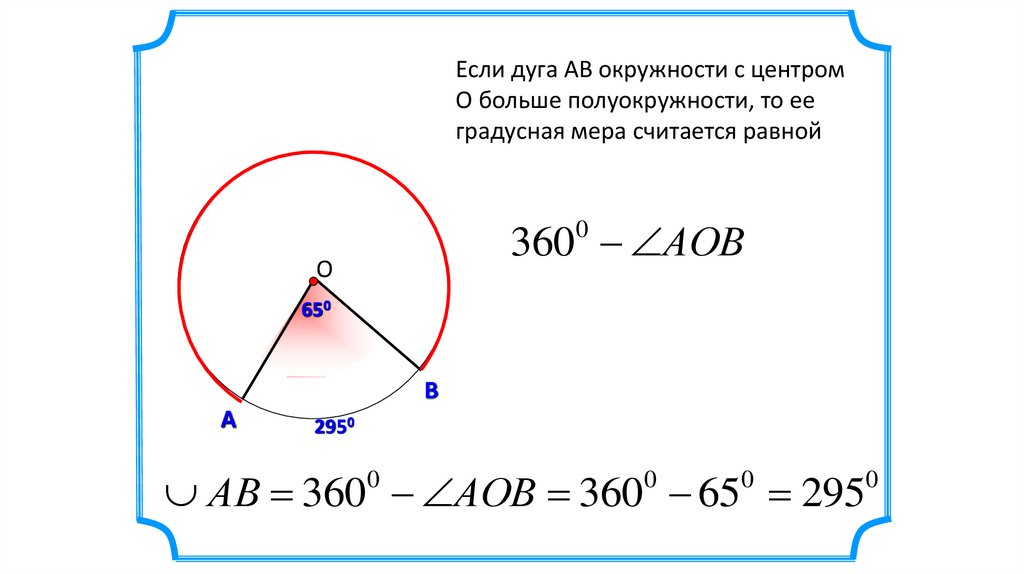
Если дуга АВ окружности с центром
О больше полуокружности, то ее
градусная мера считается равной
360 АОВ
0
О
650
В
А
2950
АВ 360 АОВ 360 65 295
0
0
0
0

6.

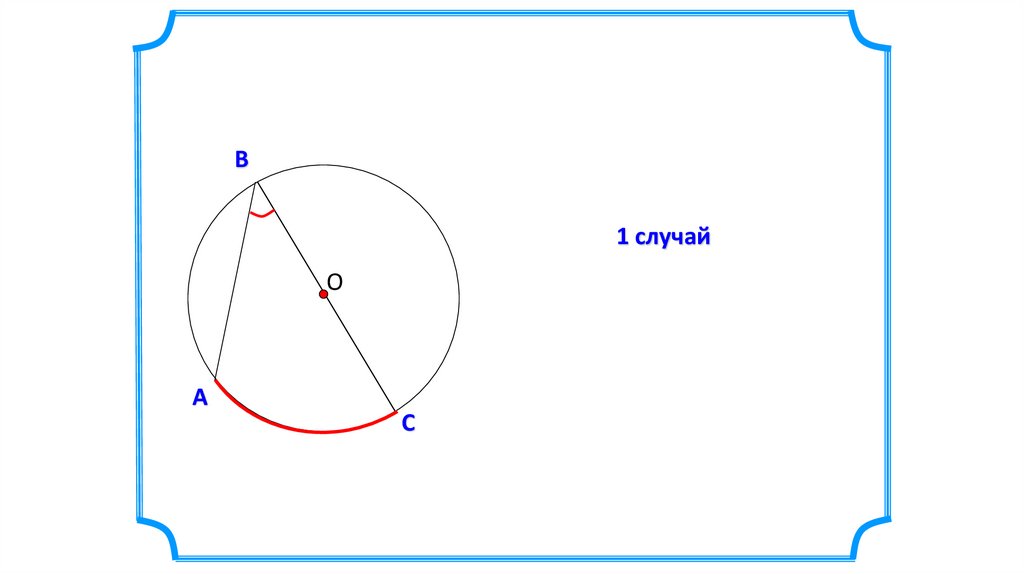
В
1 случай
О
А
С

7.

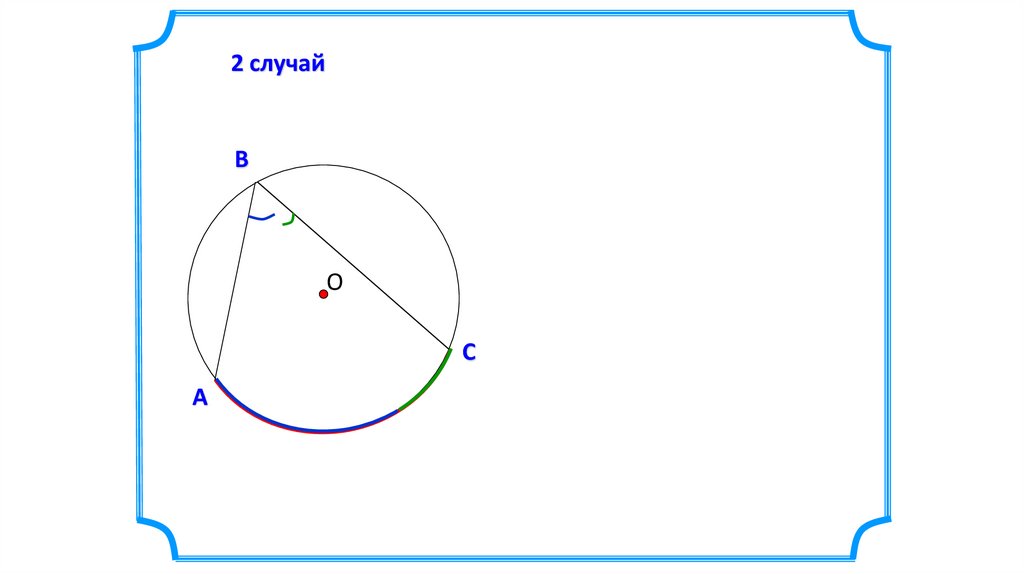
2 случай
В
О
С
А

8.

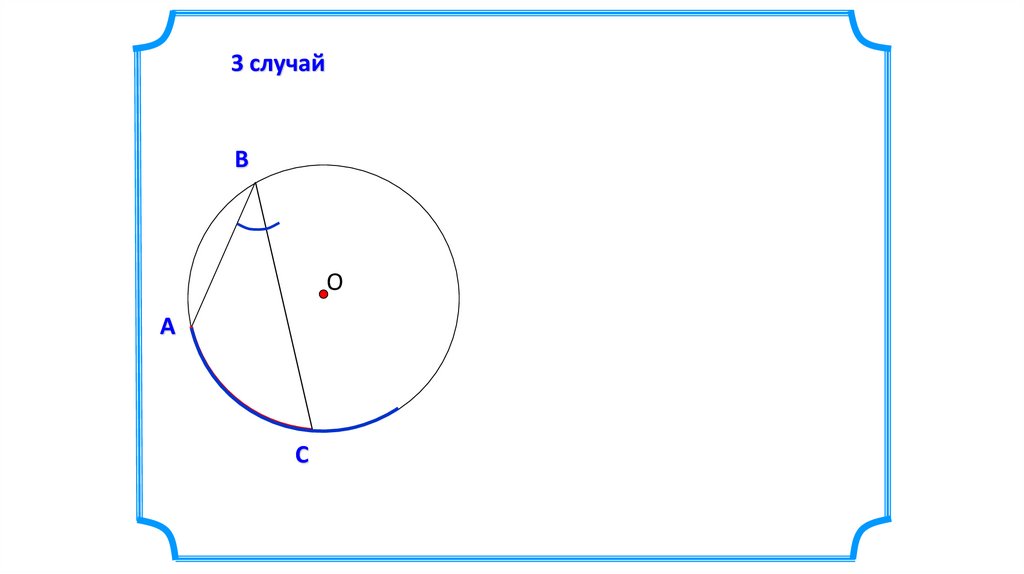
3 случай
В
О
А
С

9.

Теорема. Вписанный угол измеряется половиной
дуги, на которую он опирается.
В
Дано: АВС – вписанный
1
Доказать: АВС АС
2
a
О
1 случай (О
a 2a
А
В =
a
АС 2a
А В
=a
Тогда внешний угол АОС =
2a
АС 2a
АВС р/б
С
ВС)
1
В АС
2

10.

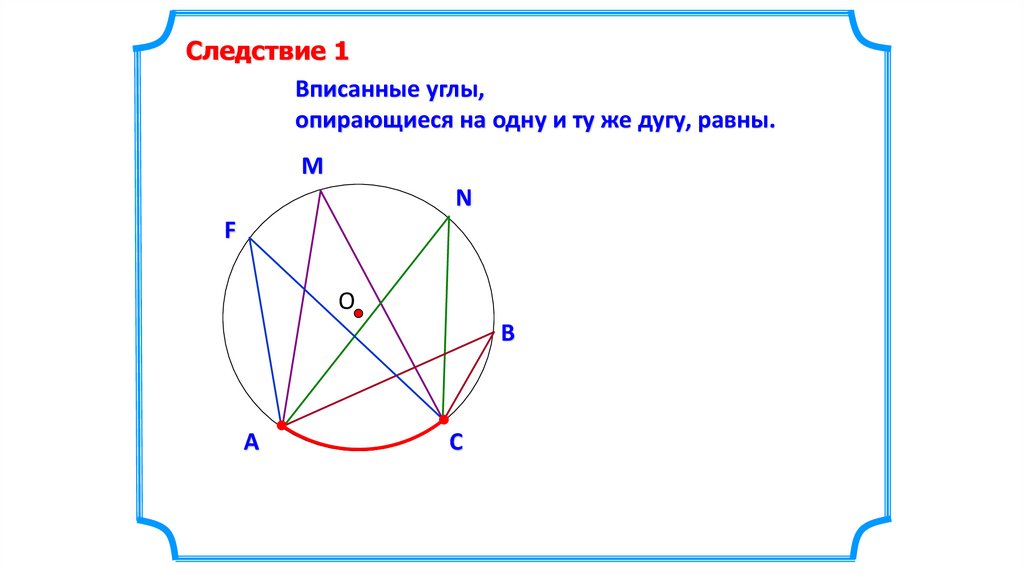
Следствие 1
Вписанные углы,
опирающиеся на одну и ту же дугу, равны.
M
N
F
О
В
А
С

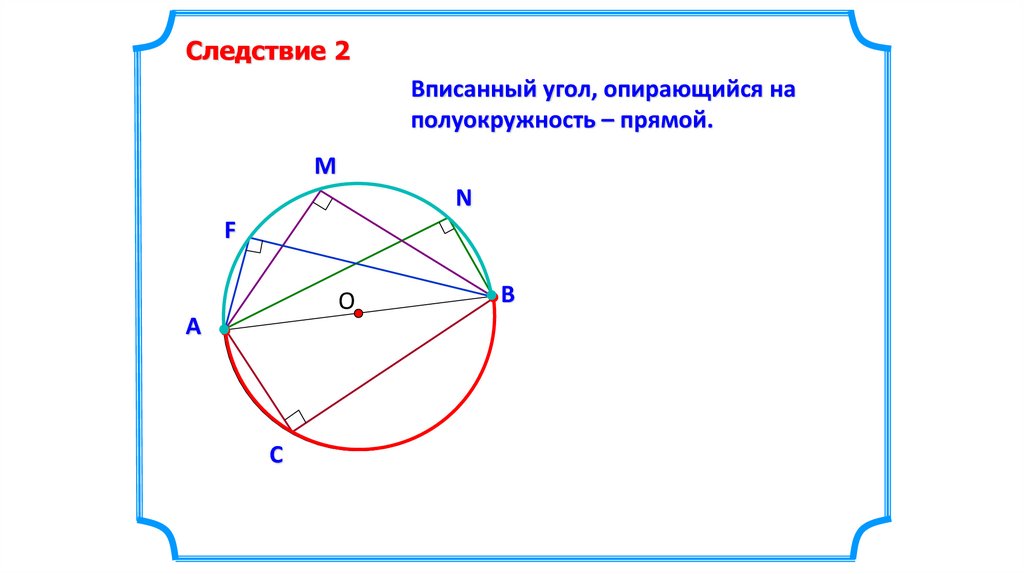
11.

Следствие 2
Вписанный угол, опирающийся на
полуокружность – прямой.
M
N
F
О
А
С
В