Медиана, биссектриса, высота треугольника

1.

2.

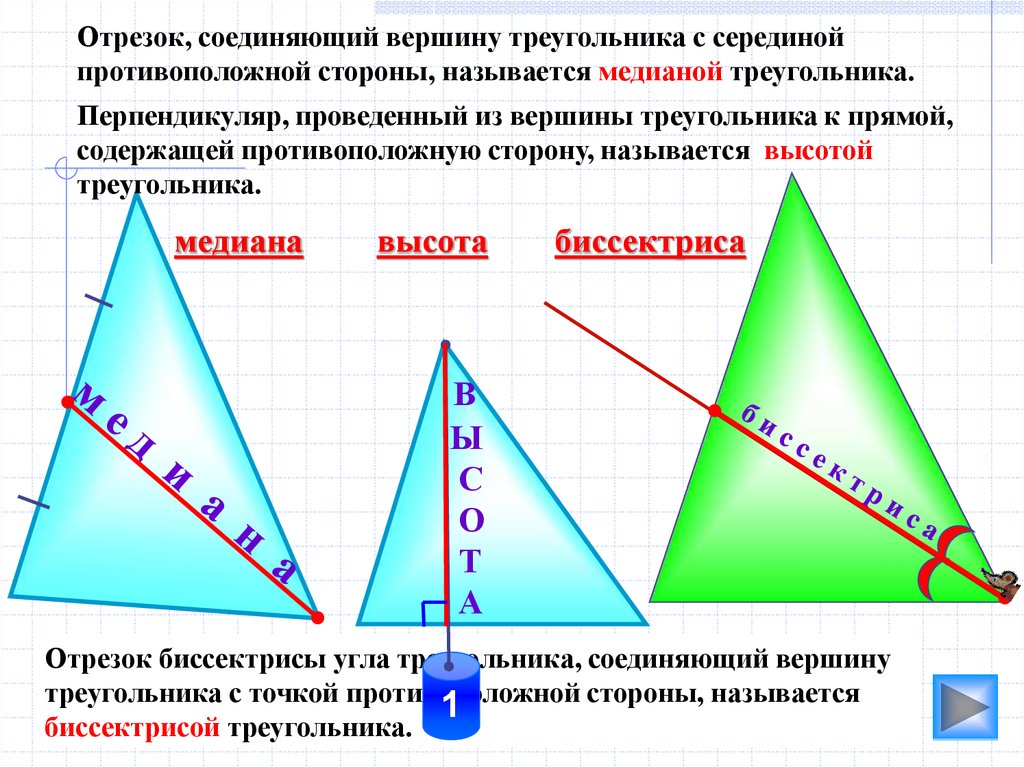
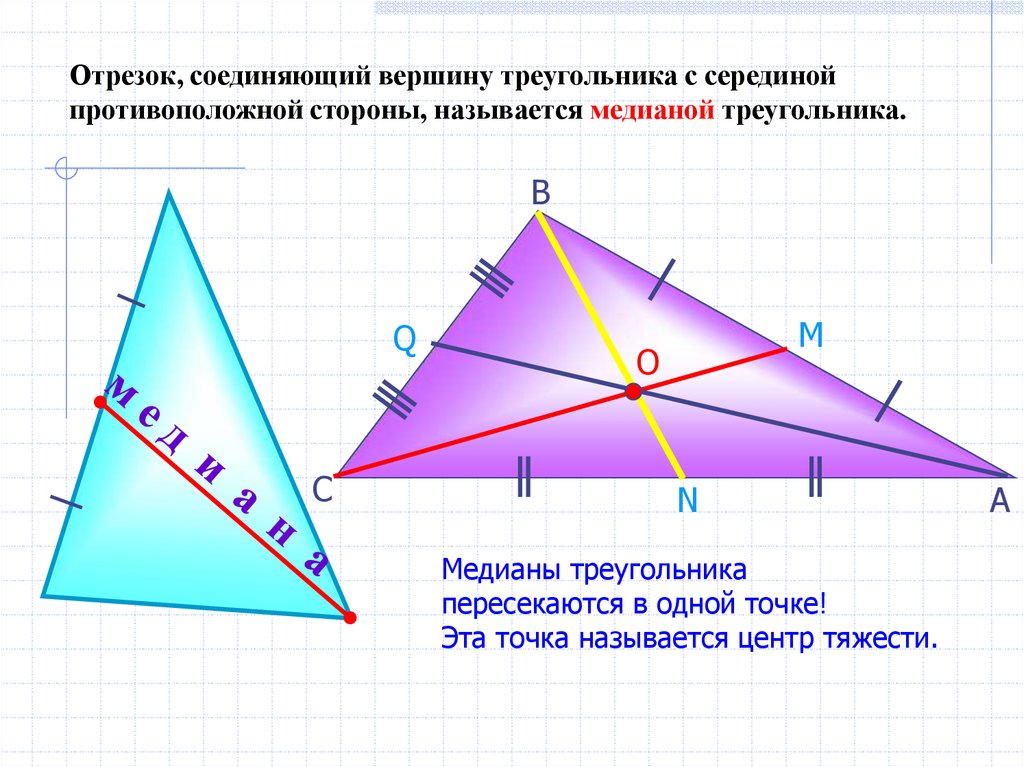
Отрезок, соединяющий вершину треугольника с серединой
противоположной стороны, называется медианой треугольника.
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
медиана
высота
биссектриса
В
Ы
С
О
Т
А
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны, называется
1
биссектрисой треугольника.

3.

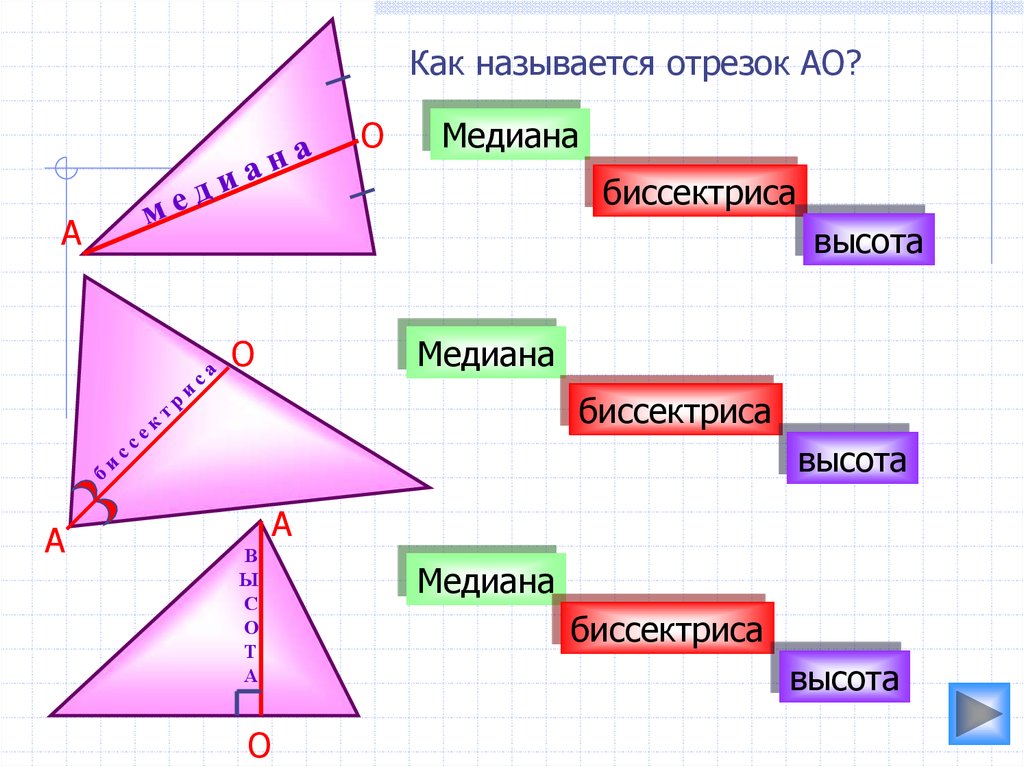
Как называется отрезок АО?
О
Медиана
биссектриса
А
высота
О
Медиана
биссектриса
высота
А
А
В
Ы
С
О
Т
А
О
Медиана
биссектриса
высота

4.

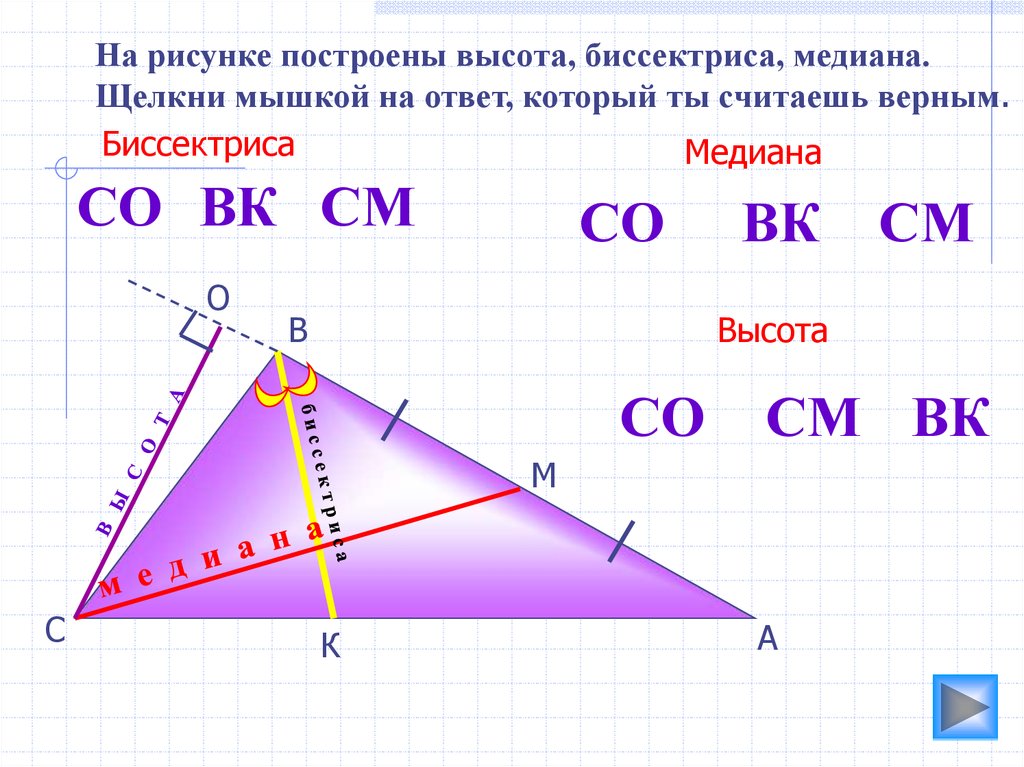
На рисунке построены высота, биссектриса, медиана.
Щелкни мышкой на ответ, который ты считаешь верным.
Биссектриса
Медиана
СО ВК СМ
О
СО
В
ВК
Высота
СО
СМ ВК
М
С
СМ
К
А

5.

О каком отрезке это определение. а) Щёлкни мышкой по названию.
б) Щёлкни мышкой по чертежу, где ты нашел этот отрезок.
Перпендикуляр, проведенный из вершины треугольника
к прямой, содержащей противоположную сторону…
биссектриса
молодец!
медиана
высота
В
Ы
С
О
Т
А
Щелкни мышкой по другим картинкам.

6.

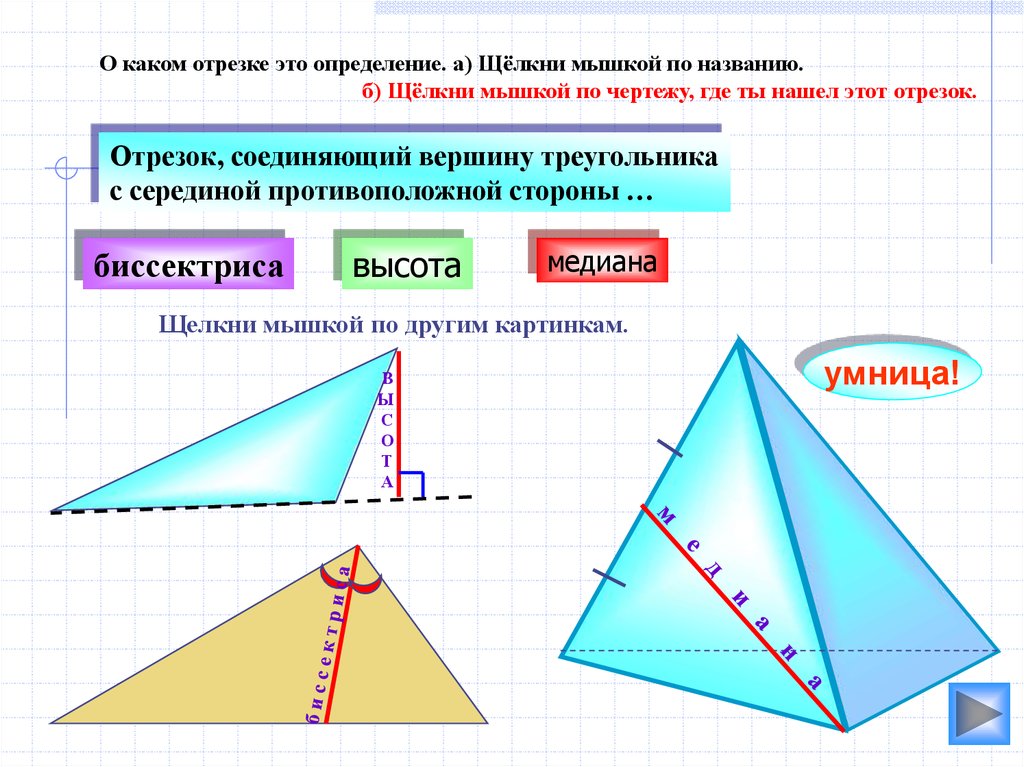
О каком отрезке это определение. а) Щёлкни мышкой по названию.
б) Щёлкни мышкой по чертежу, где ты нашел этот отрезок.
Отрезок, соединяющий вершину треугольника
с серединой противоположной стороны …
биссектриса
высота
медиана
Щелкни мышкой по другим картинкам.
В
Ы
С
О
Т
А
умница!

7.

Отрезок, соединяющий вершину треугольника с серединой
противоположной стороны, называется медианой треугольника.
В
Q
С
М
O
N
Медианы треугольника
пересекаются в одной точке!
Эта точка называется центр тяжести.
А

8.

Треугольник, который опирается на острие иглы в точке пересечения
медиан, находится в равновесии! Точка, обладающая таким
свойством, называется центром тяжести треугольника.
Треугольник, который опирается на опору по линии медианы,
находится в равновесии.

9.

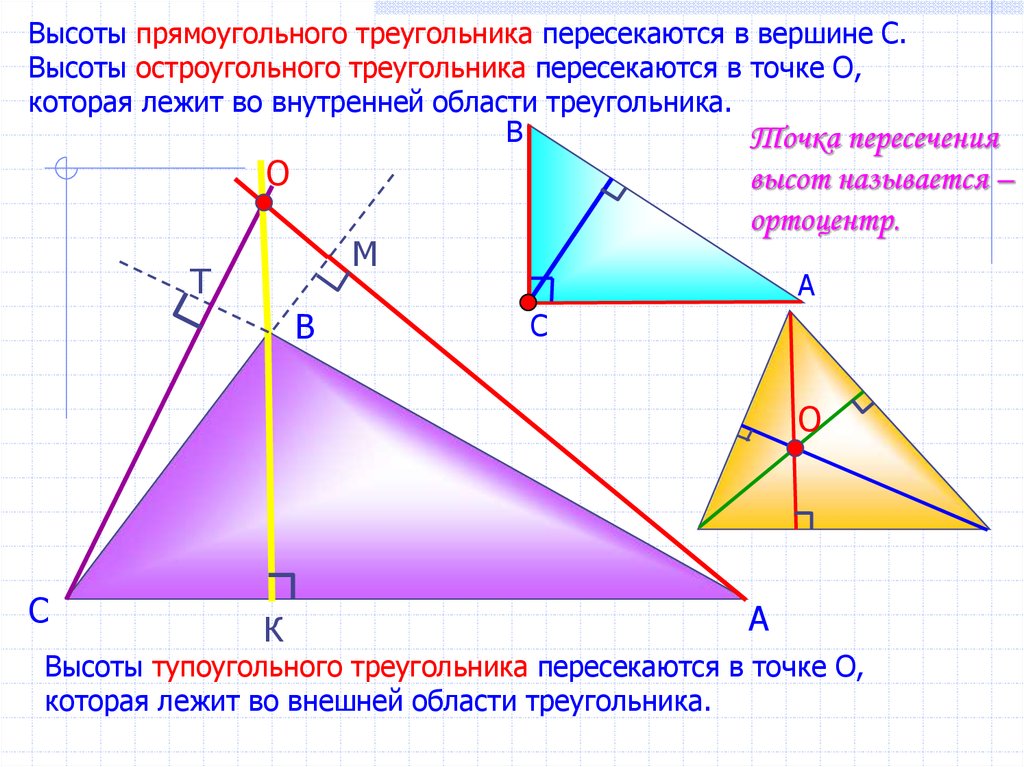
Высоты прямоугольного треугольника пересекаются в вершине С.
Высоты остроугольного треугольника пересекаются в точке О,
которая лежит во внутренней области треугольника.
В
Точка пересечения
O
высот называется –
ортоцентр.
М
Т
В
А
С
O
С
К
А
Высоты тупоугольного треугольника пересекаются в точке О,
которая лежит во внешней области треугольника.

10.

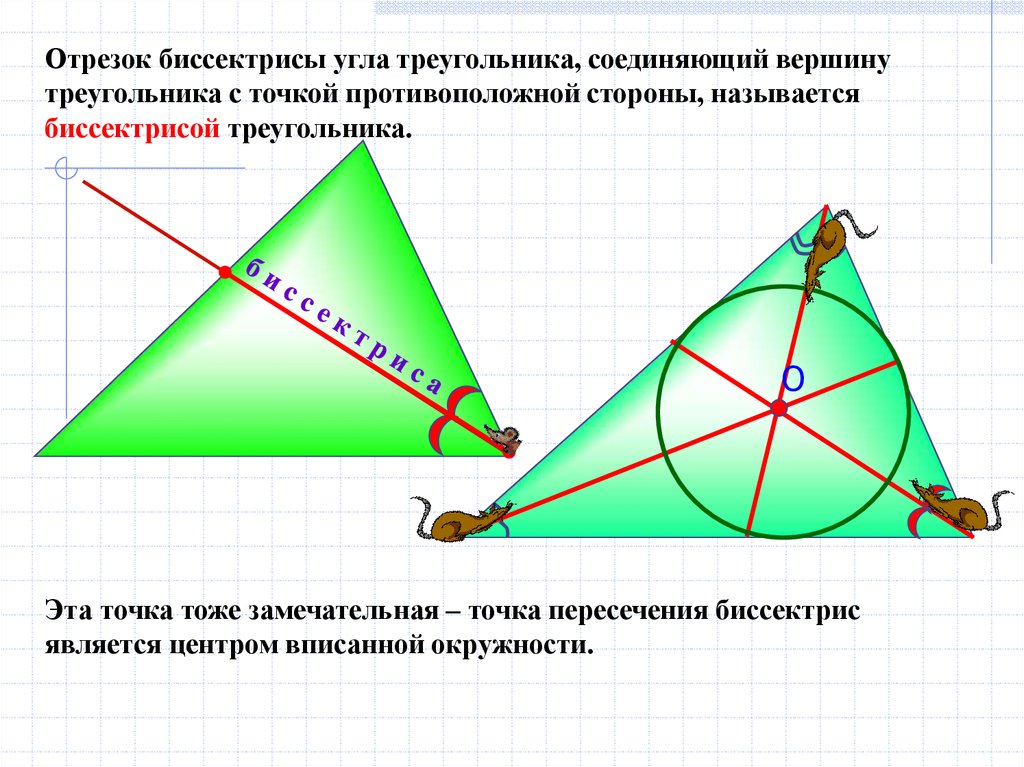
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны, называется
биссектрисой треугольника.
O
Эта точка тоже замечательная – точка пересечения биссектрис
является центром вписанной окружности.

11.

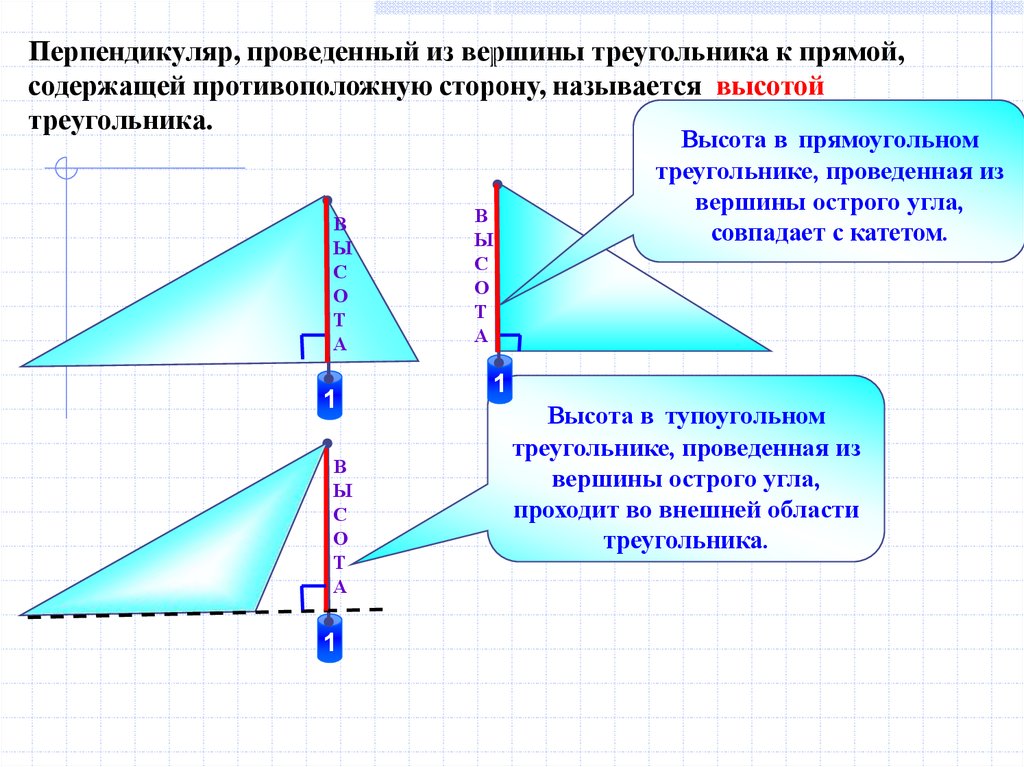
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
Высота в прямоугольном
треугольнике, проведенная из
вершины острого угла,
совпадает с катетом.
1
Высота в тупоугольном
треугольнике, проведенная из
вершины острого угла,
проходит во внешней области
треугольника.

12.

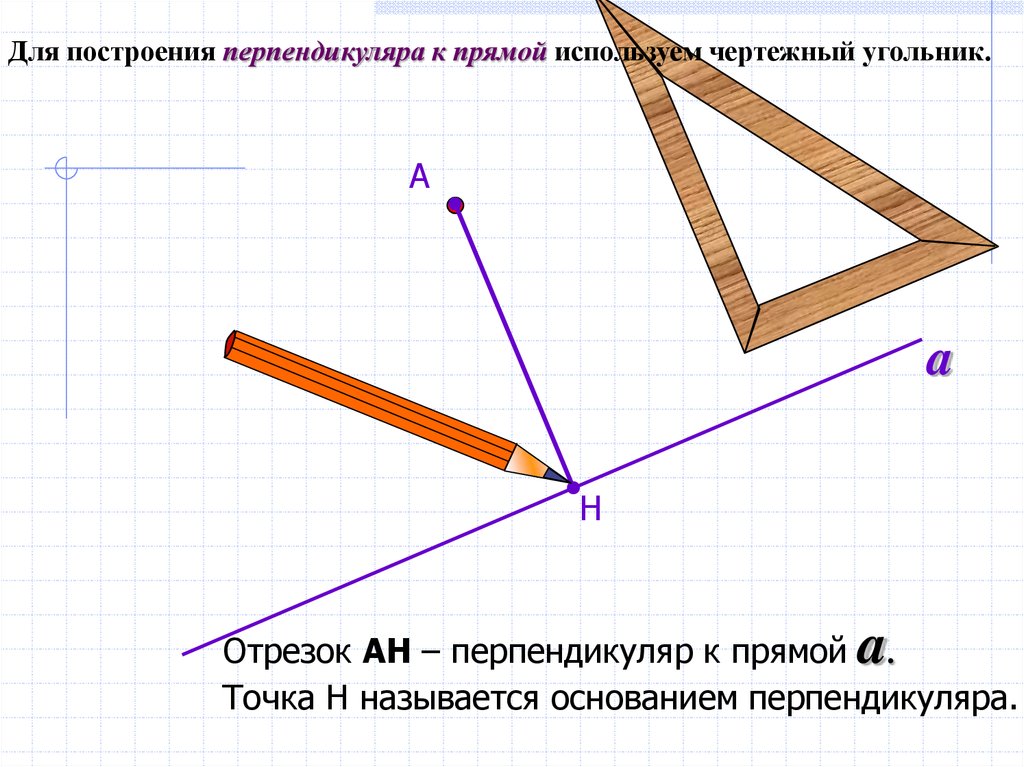
Для построения перпендикуляра к прямой используем чертежный угольник.
А
a
Н
a
Отрезок АН – перпендикуляр к прямой .
Точка Н называется основанием перпендикуляра.

13.

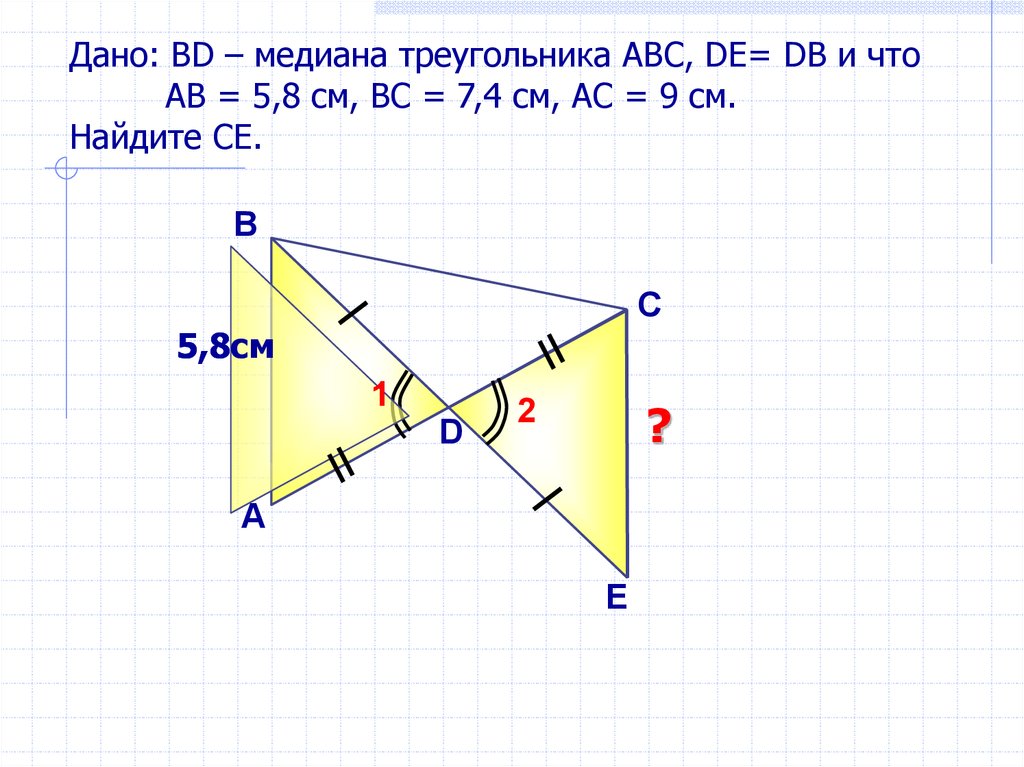
Дано: ВD – медиана треугольника АВС, DE= DB и что
АВ = 5,8 см, ВС = 7,4 см, АС = 9 см.
Найдите СЕ.
В
С
5,8см
1
D
?
2
А
E

14.

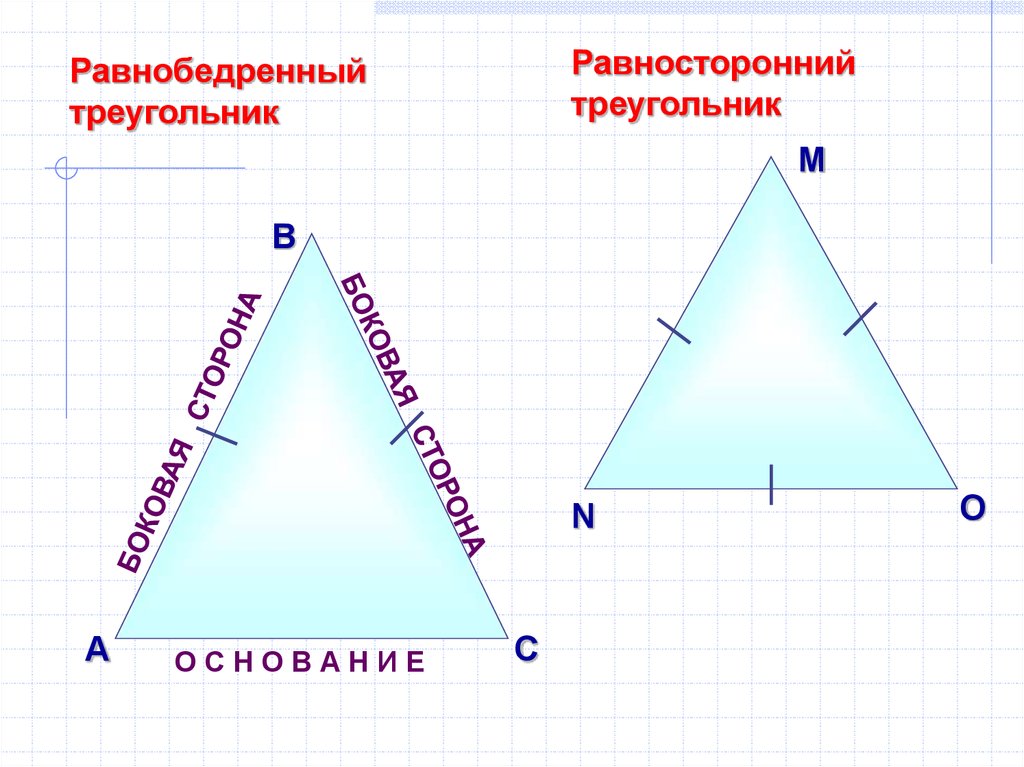
Равносторонний
треугольник
Равнобедренный
треугольник
M
В
N
А
ОСНОВАНИЕ
С
O

15.

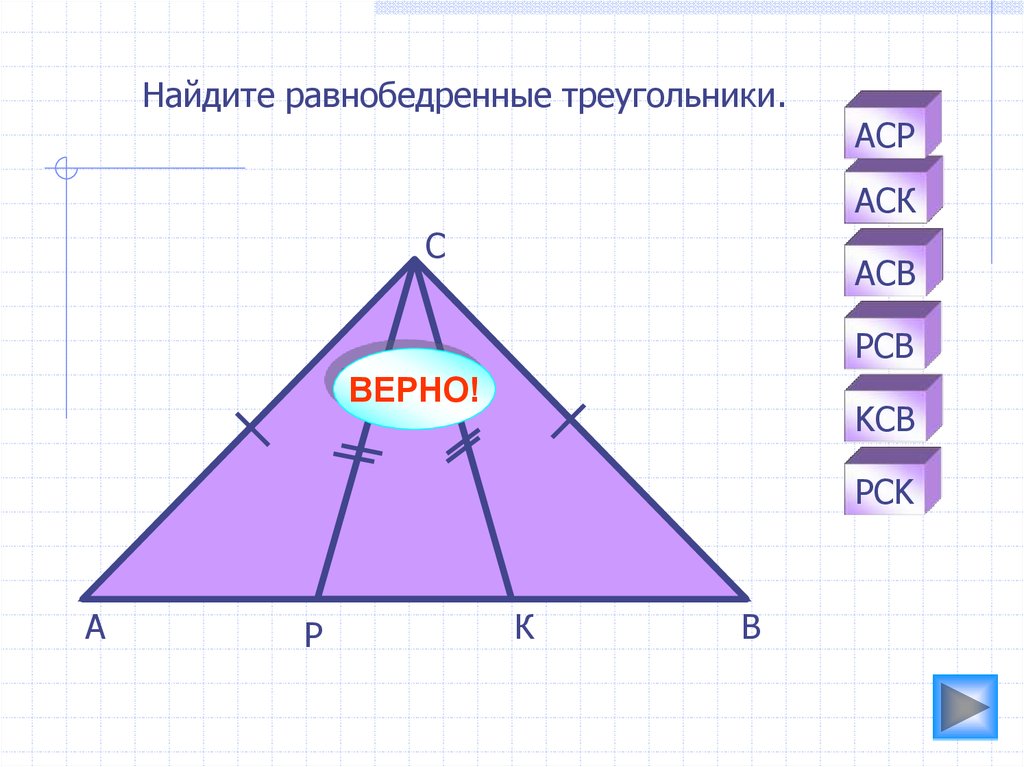
Найдите равнобедренные треугольники.
АСР
АСК
С
АСВ
PCB
ВЕРНО!
KCB
PCK
А
Р
К
В

16.

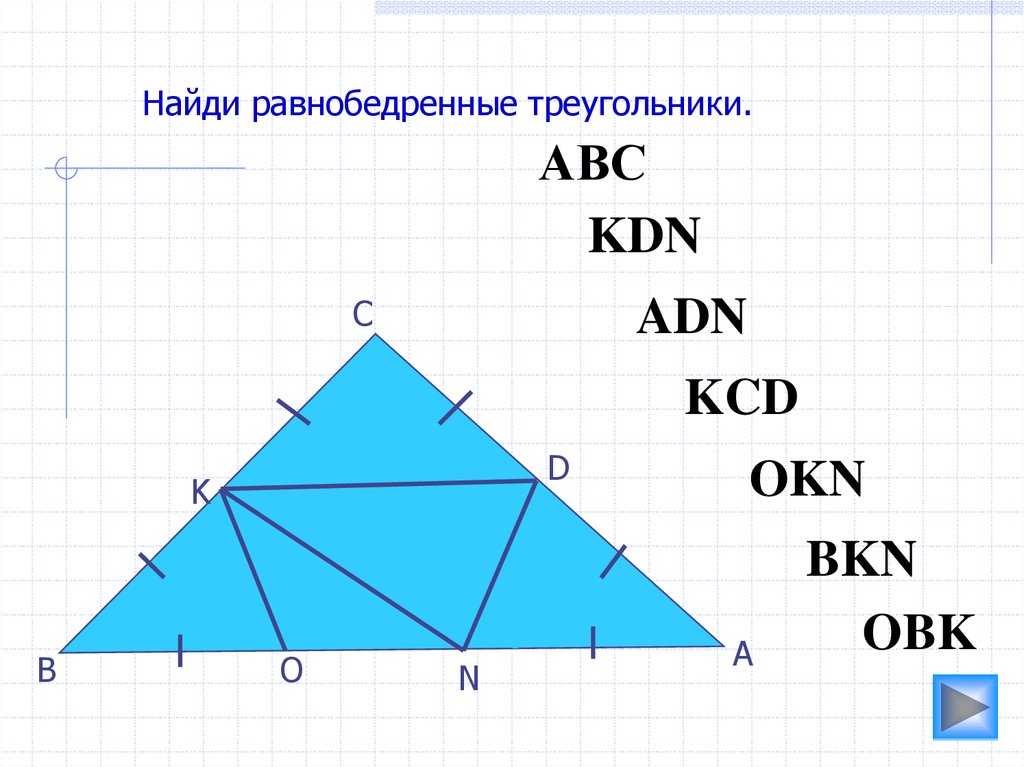
Найди равнобедренные треугольники.
АВС
KDN
С
ADN
KCD
D
K
В
O
N
OKN
А
BKN
OBK

17.

Сколько всего равнобедренных треугольников
можно заметить на рисунке?
Не верно!
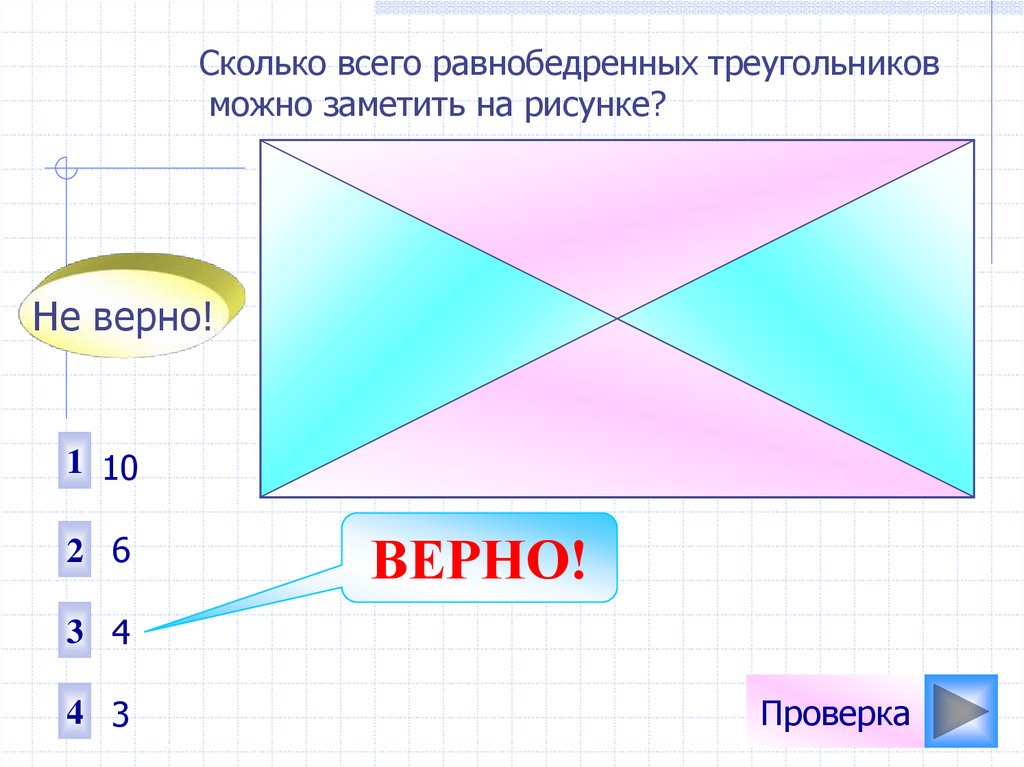
1 10
2 6
ВЕРНО!
3 4
4 3
Проверка

18.

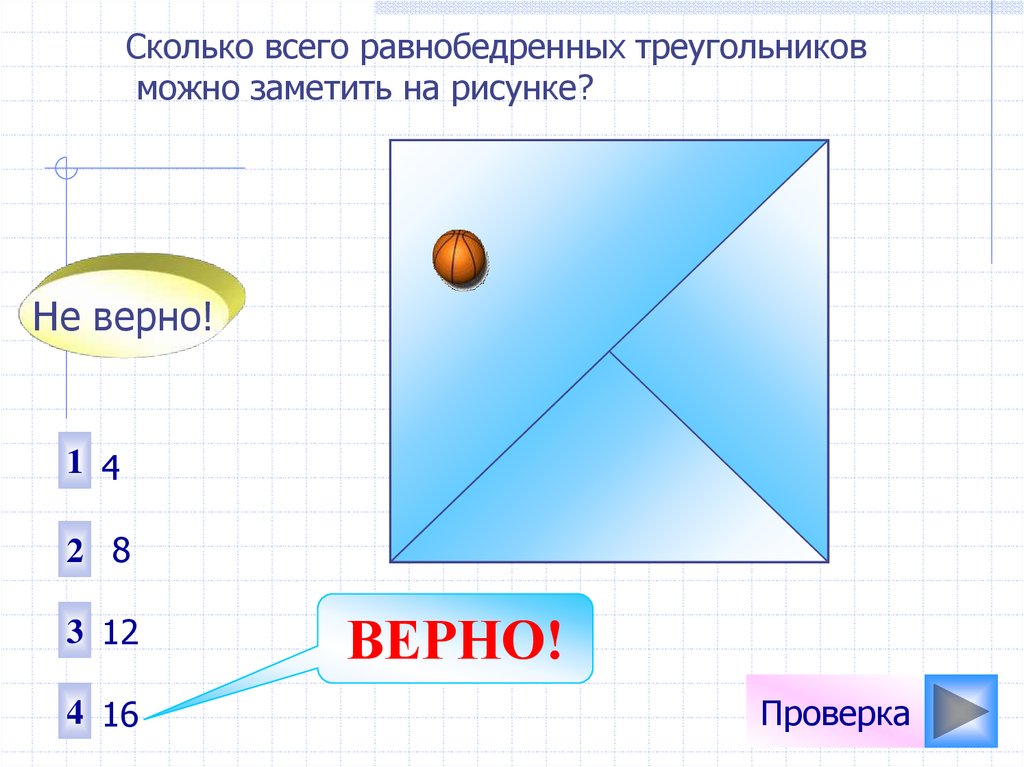
Сколько всего равнобедренных треугольников
можно заметить на рисунке?
Не верно!
1 4
2 8
3 12
4 16
ВЕРНО!
Проверка

19.

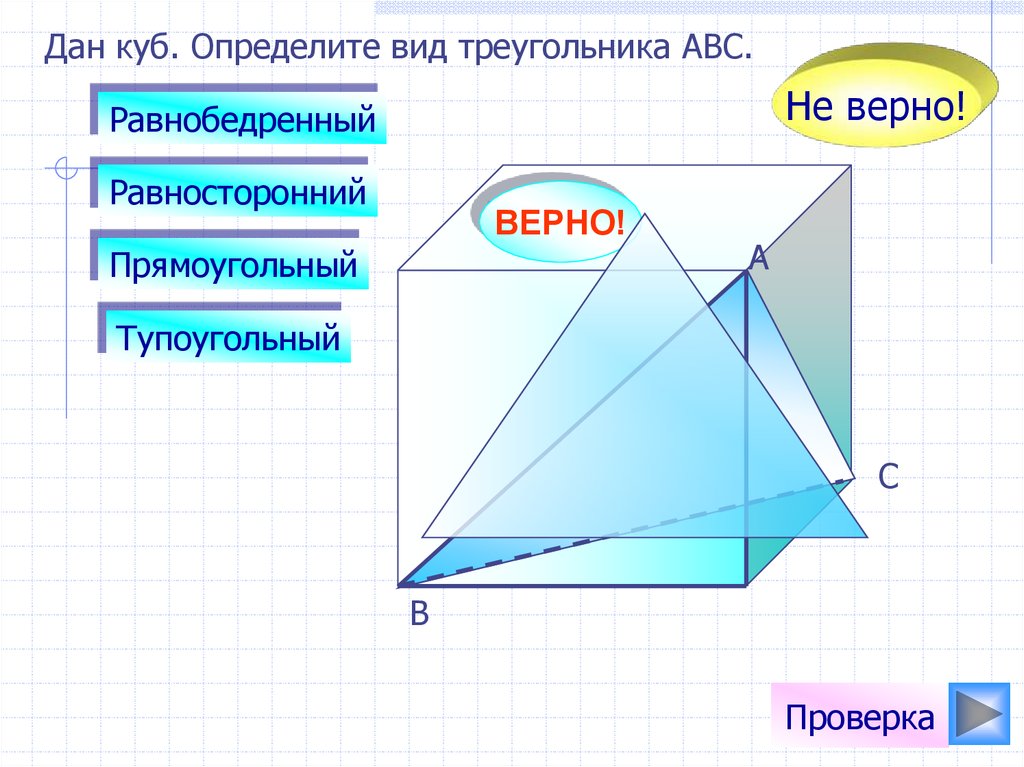
Дан куб. Определите вид треугольника АВС.
Не верно!
Равнобедренный
Равносторонний
ВЕРНО!
Прямоугольный
А
Тупоугольный
С
В
Проверка

20.

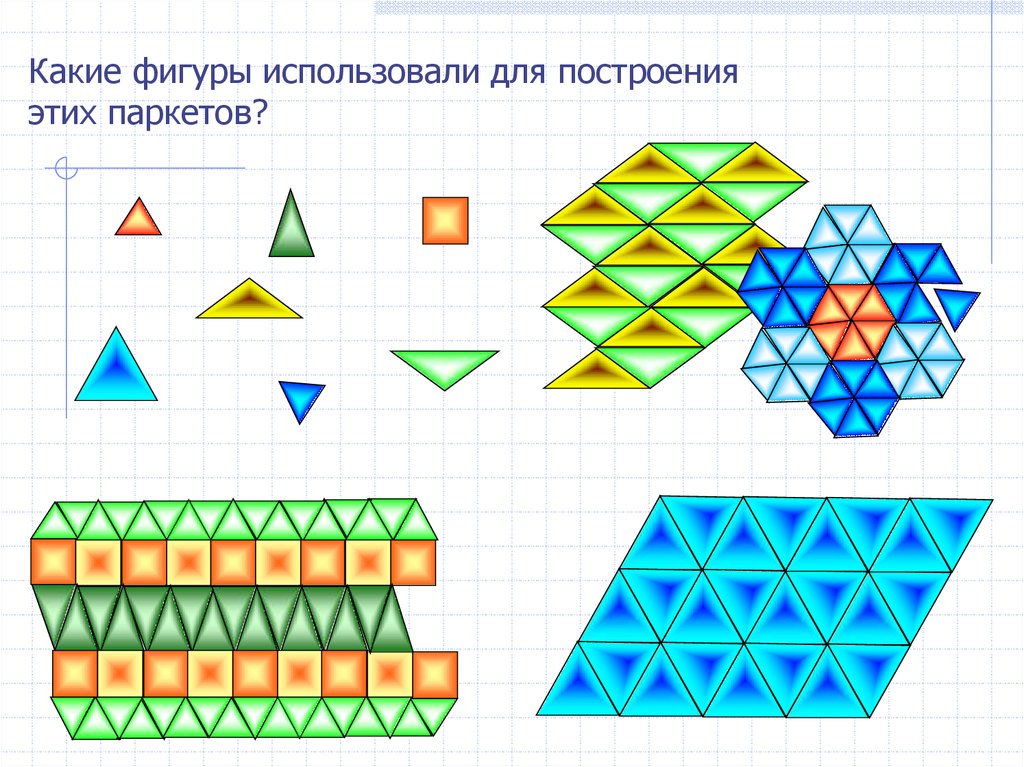
Какие фигуры использовали для построения
этих паркетов?

21.

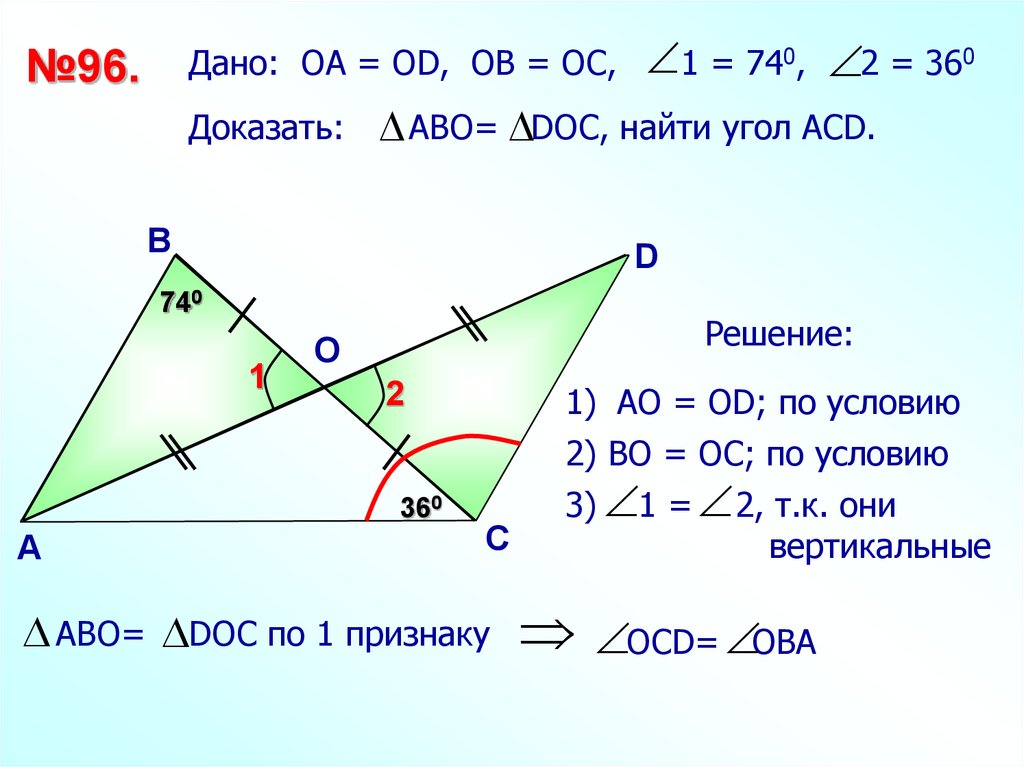
№96.
Дано: ОА = ОD, ОВ = ОС,
Доказать:
АВО= DОС, найти угол АСD.
B
D
740
1
Решение:
О
2
360
А
1 = 740, 2 = 360
C
АВО= DОС по 1 признаку
1) АО = ОD; по условию
2) ВО = ОС; по условию
3) 1 = 2, т.к. они
вертикальные
ОСD= ОВА

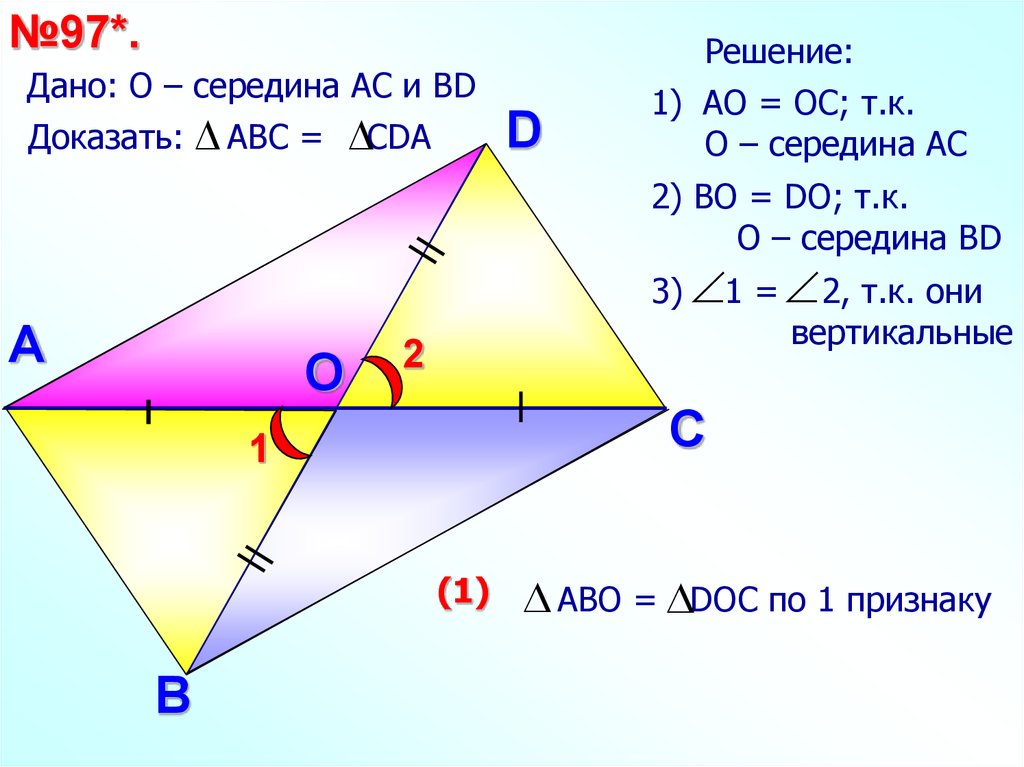
22.

№97*.
Дано: О – середина АС и ВD
Доказать: AВС = СDА
D
Решение:
1) АО = ОC; т.к.
О – середина АС
2) ВО = DO; т.к.
О – середина ВD
A
O
3) 1 = 2, т.к. они
вертикальные
2
С
1
(1)
В
АВО = DОС по 1 признаку

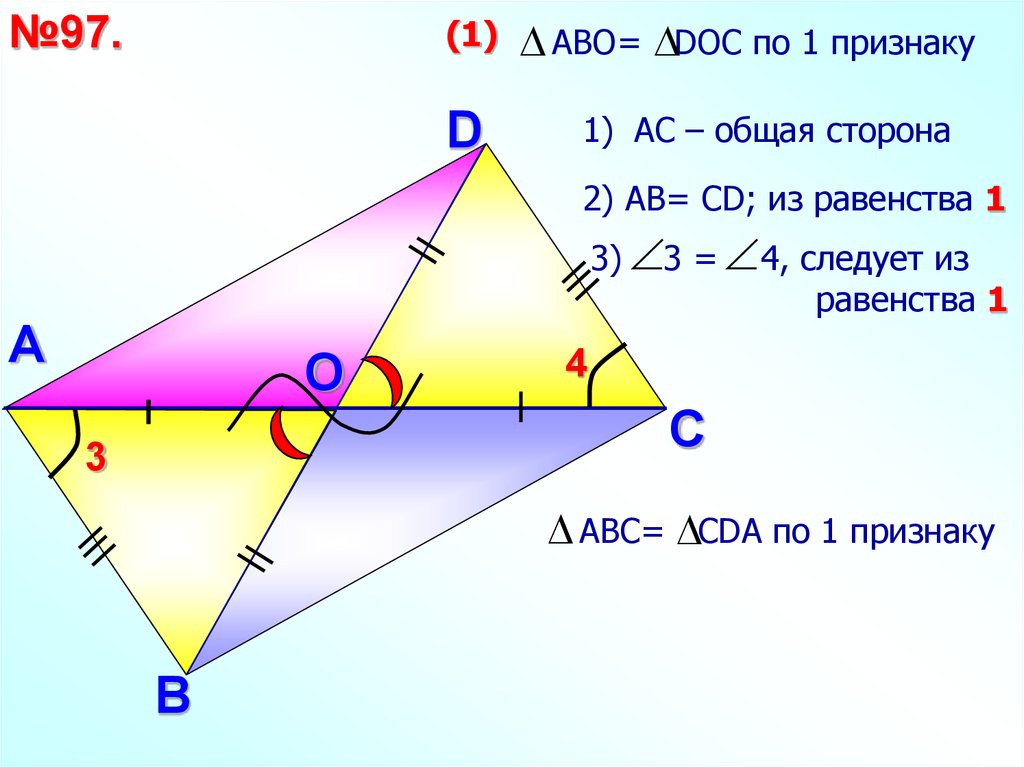
23.

№97.
(1)
D
АВО= DОС по 1 признаку
1) АС – общая сторона
2) АВ= СD; из равенства 1
3) 3 = 4, следует из
равенства 1
A
O
3
4
С
АВС= СDА по 1 признаку
В