Применение производной к исследованию функций

1.

2.

Метод математических моделей в экономике
Что же такое математическая модель?
Определение:
Математическая модель - приближенное описание какого-либо
явления внешнего мира, выраженное с помощью математической
символики и заменяющее изучение этого явления исследованием и
решением математических задач.
© Тамбов, МАОУ СОШ № 31, 2016

3.

Метод математических моделей в экономике
Что называется математическим моделированием?
Изучение явлений с помощью математических
моделей называется математическим
моделированием.
Схематический процесс математического моделирования:
Уточнение модели
Явление внешнего мира.
Его приближенное описание. Запись основных свойств и
соотношений между ними на математическом языке,
формулировка основных математических задач.
Решение математических задач, исследование решений.
Выводы. Новые свойства изучаемого явления, прогнозы,
сравнение с известными результатами.
© Тамбов, МАОУ СОШ № 31, 2016

4.

5.

6.

Алгоритм для решения задач
Памятка по решению задач на оптимизацию
1 этап. Составление математической модели.
Проанализировав условия задачи, выделите оптимизируемую величину, т.е. величину, о
наибольшем или наименьшем значении которой идет речь. Обозначьте ее, например,
буквой F.
Участвующие в задаче неизвестные величины, через которые нетрудно выразить
оптимизируемую величину, примите за независимые переменные и обозначьте их
буквами х, у (или какими-либо другими буквами). Установите реальные границы
изменения независимых переменных в соответствии с условиями задачи.
Исходя из условия задачи, выразите все величины через одну переменную, в том числе и
оптимизируемую величину. Математическая модель задачи представляет собой функцию
F=f(х) с областью определения x, которую нашли на втором шаге.
II этап. Работа с составленной моделью.
На этом этапе для функции F=f(х), х ∈Х найдите наименьшее или наибольшее значение в
зависимости от того, что требуется в условии задачи. При этом используются
теоретические установки: исследование функции с помощью производной.
III этап. Ответ на вопрос задачи.
Здесь следует получить конкретный ответ на вопрос задачи, опираясь на результаты,
полученные на этапе работы с моделью. Записать ответ в терминах предложенной задачи.

7.

Фермеру выделили участок прямоугольной формы с периметром 56 м.
Какими должны быть стороны участка, чтобы посевная площадь оказалась
наибольшей?
Решение.
1. 1 этап. Составление математической модели.
Пусть х см – одна из сторон прямоугольника;
у см – вторая сторона прямоугольника;
2(х + у) см – периметр прямоугольника, который по условию
равен 56 см. [ 2(х + у) = 56 ]
Тогда S = х у - площадь прямоугольника.
Выразим у через х:
2(х + у) = 56
х + у = 28
у = 28 – х ; т.к х, у – длины сторон, то х > 0; у > 0
т.е. х 0;28
Тогда S = х ( 28 х) - площадь прямоугольника.

8.

1. 2 этап. Работа с составленной моделью.
Рассмотрим функцию S(х) = х ( 28 х) и найдём ее наибольшее
значение на х 0;28 .
D(s) = R
s ( x) 28x x
s ( x ) 0
28 2x 0
x = 14
2
28 2x ;
0
14
28
14 – точка максимума на х 0;28 , наибольшее значение функции на
промежутке достигается в этой точке.
max s(x) = s(14) = 14(28 – 14) = 196 – наибольшее значение функции.
0; 28
2. 3 этап. Ответ на вопрос задачи.
х = 14 ; 14 см – одна из сторон прямоугольника;
у = 28 – 14 = 14; 14 см – вторая сторона прямоугольника;
S = х у = 196 см2 – наибольшая площадь прямоугольника.
Ответ: 14;14 см; 196 см2.

9.

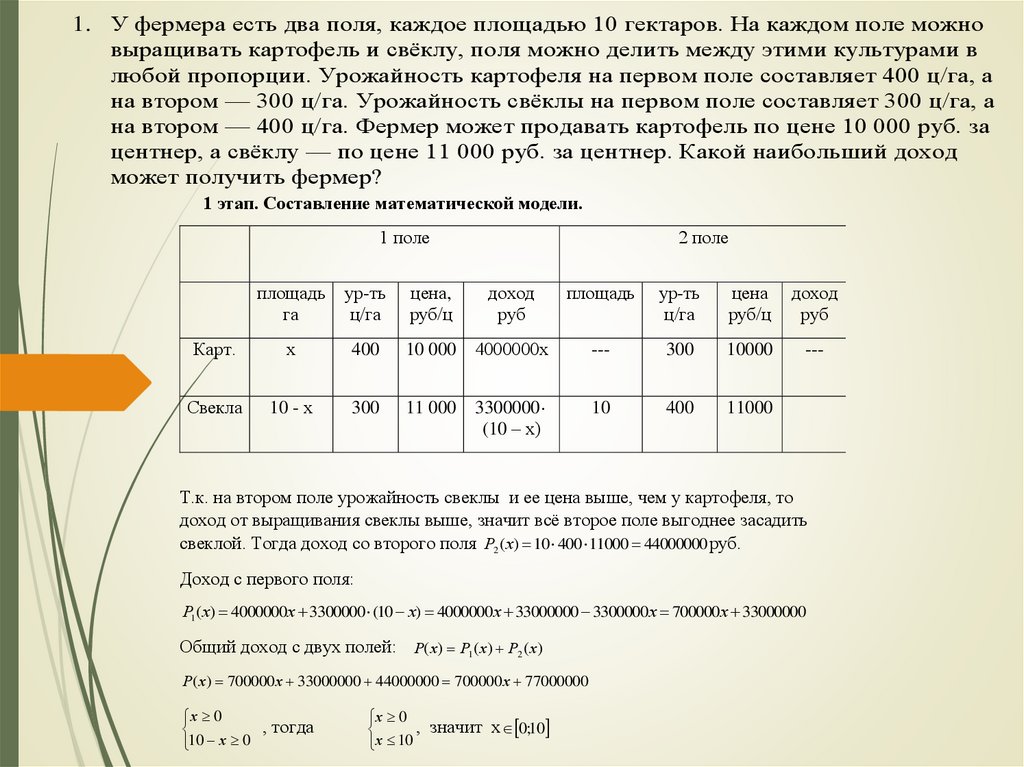
1. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно
выращивать картофель и свёклу, поля можно делить между этими культурами в
любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а
на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а
на втором — 400 ц/га. Фермер может продавать картофель по цене 10 000 руб. за
центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход
может получить фермер?
1 этап. Составление математической модели.
1 поле
площадь
га
ур-ть
ц/га
цена,
руб/ц
Карт.
х
400
Свекла
10 - х
300
11 000
2 поле
доход
руб
площадь
ур-ть
ц/га
цена
руб/ц
доход
руб
10 000 4000000х
---
300
10000
---
3300000
(10 – х)
10
400
11000
Т.к. на втором поле урожайность свеклы и ее цена выше, чем у картофеля, то
доход от выращивания свеклы выше, значит всё второе поле выгоднее засадить
свеклой. Тогда доход со второго поля Р2 ( х) 10 400 11000 44000000 руб.
Доход с первого поля:
Р1 ( х) 4000000х 3300000 (10 х) 4000000х 33000000 3300000х 700000х 33000000
Общий доход с двух полей: Р( х) Р1( х) Р2 ( х)
Р( х) 700000 х 33000000 44000000 700000 х 77000000
х 0
, тогда
10 х 0
х 0
, значит х 0;10
х 10

10.

2 этап. Работа с составленной моделью.
Рассмотрим функцию Р( х) 700000 х 77000000 и найдём наибольшее значение
этой функции на отрезке х 0;10 .
D(P) = R;
Р ( х) 700000
Р ( х) 700000 0 для всех значений х, значит функция возрастает
Р
Р
значит наибольшее значение
достигается при х = 10
Р(10) = 700000 10 + 77000000 = 84000000 руб.
0
10
3 этап. Ответ на вопрос задачи.
84000000 руб – наибольший доход, который может получить фермер.
Ответ: 84000000 руб.