Производная в исследовании функций. Занятие 104

1. Занятие 104. Производная в исследовании функций

Математика
Занятие 104.
Производная в исследовании
функций
3.Теорема Вейерштрасса
4. Экстремальные задачи

2. Теорема Вейерштрасса

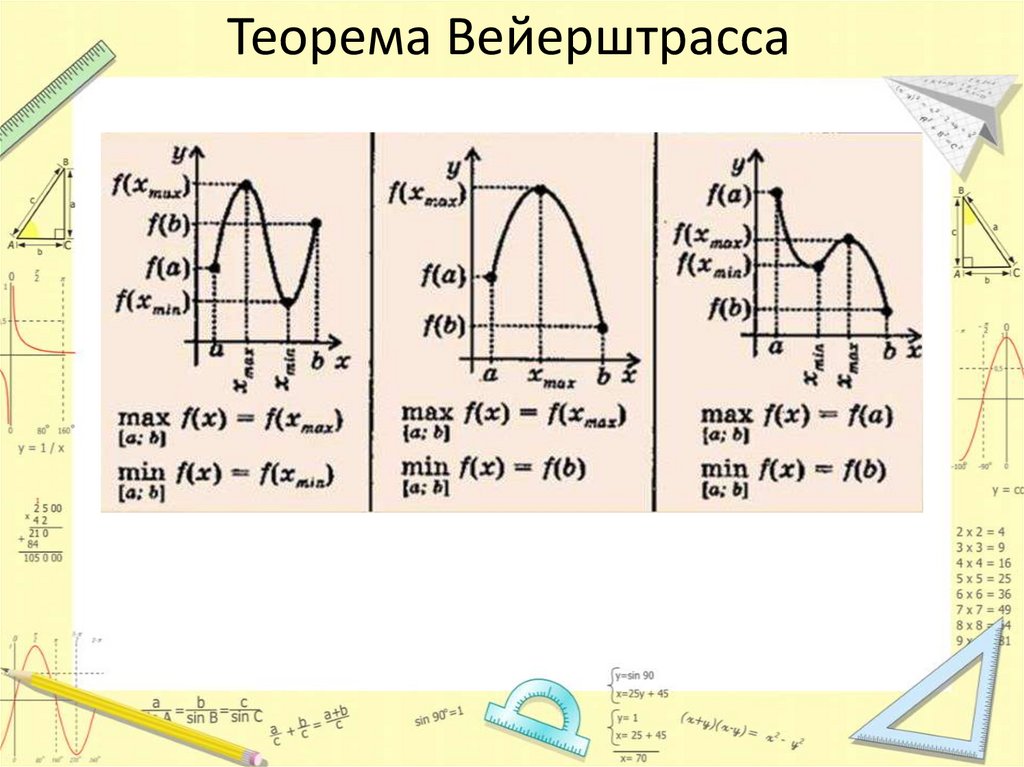
Нахождение наибольшего и наименьшего
значений непрерывной функции y=f(x) на
отрезке [a;b].
Теорема (1)
Непрерывная на отрезке [a;b] функция
y=f(x) достигает своих наибольшего и
наименьшего значений либо на концах
этого отрезка, либо в критических
точках, принадлежащих ему.

3. Теорема Вейерштрасса

4. Теорема Вейерштрасса

Алгоритм
1. Найти критические точки функции y=f(x).
2. Выбрать из них те, которые принадлежат
отрезку [a;b].
3. Вычислить значения функции в выбранных
точках и на концах отрезка.
4. Выбрать среди этих значений наименьшее и
наибольшее.

5. Теорема Вейерштрасса

Задача 1. Найти наибольшее и наименьшее значения
функции y=f(x) на [a;b]:
а) y x 4 8 x 2 12 , 0;3
Решение: D( y )
y ( x 4 ) 8( x 2 ) (12) 4 x 3 8 * 2 x 4 x 3 16 x
4 x 3 16 x 0 4 x( x 2 4) 0 4 x 0 или
x1 0, x2 2, x3 2
0 0;3 , 2 0;3 , 2 0;3
f (0) 0 4 8 * 0 2 12 12
f (2) 2 4 8 * 2 2 12 16 32 12 4
f (3) 34 8 * 32 12 81 72 12 21
Ответ : max f ( x) f (3) 21; min f ( x) f (2) 4
0;3
0;3
x2 4 0

6. Теорема Вейерштрасса

Задача 1. Найти наибольшее и наименьшее значения
функции y=f(x) на [a;b]:
б) y x 4 8 x 2 12 , 3;4
Решение: D( y )
y ( x 4 ) 8( x 2 ) (12) 4 x 3 8 * 2 x 4 x 3 16 x
4 x 3 16 x 0 4 x( x 2 4) 0 4 x 0 или
x1 0, x2 2, x3 2
0 3;4 , 2 3;4 , 2 3;4
f (3) 34 8 * 32 12 81 72 12 21
f (4) 4 4 8 * 4 2 12 256 128 12 140
Ответ : max f ( x) f (4) 140; min f ( x) f (3) 21
0;3
0;3
x2 4 0

7. Теорема Вейерштрасса

Задача 1. Найти наибольшее и наименьшее значения
функции y=f(x) на [a;b]:
в) y 2х , 0,5;0,5
х 1
Решение: D( y ) 1; 1
( х 2 ) ( х 2 1) х 2 ( х 2 1) 2 х( х 2 1) х 2 * 2 х 2 х 3 2 х 2 х 3
y
2
2
2
2
2
2
( х 1)
( х 1)
( х 1)
2х
2х
0
2
2
2
2
f
(
0
)
1
( х 1)
( х 1)
02 1
2х
2
0 х 0
2
( х 1)
0 0,5;0,5
0,5
0,5
50
2
0,52 1 0,75
75
3
0,5
0,5 50 2
f ( 0,5)
2
( 0,5) 1 0,75 75 3
f (0,5)
2
Ответ : max f ( x) f ( 0,5) ;
0 , 5; 0 , 5
3
min f ( x) f (0) 1
0 , 5; 0 , 5

8. Теорема Вейерштрасса

Задача 1. Найти наибольшее и наименьшее значения
функции y=f(x) на [a;b]:
г) y 2х , 0,1; 1,5
х 1
Решение:
D( y ) 1; 1
При x =1 значение функции не определено, т.е. точка
х=1 является точкой разрыва данной функции.
Тогда нельзя применить теорему Вейерштрасса, и на
отрезке [-0,1; 1,5] функция не имеет наибольшего и
наименьшего значений
Ответ: задача не имеет решения

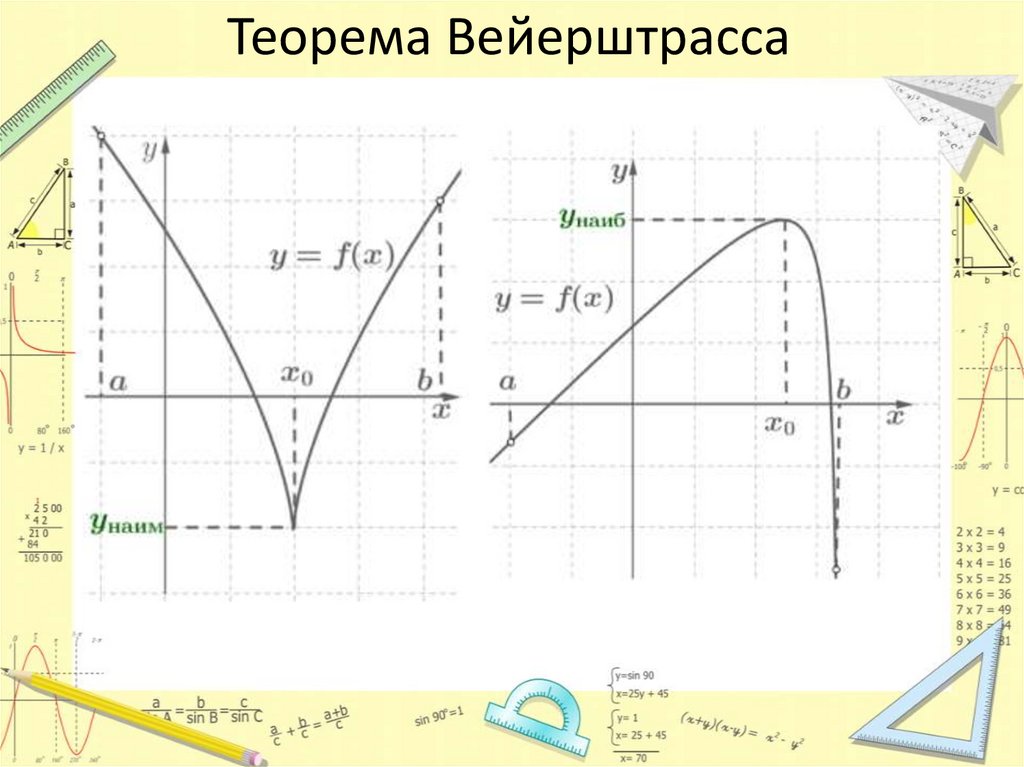
9. Теорема Вейерштрасса

А как действовать, если необходимо найти наименьшее и
наибольшее значения не на отрезке [a;b], а на интервале
(a;b)?
В этом случае решение задачи значительно усложняется, и ее
решение рассматривается в курсе высшей математики.
Но существуют два достаточно простых и часто
встречающихся случая, когда задача разрешима. Для этого
применяется следующая теорема (2).
Пусть функция y=f(x) непрерывна на интервале (a;b) и
имеет внутри него единственную критическую точку
х0, тогда:
1) если х0 – точка максимума, то ymax = f(x0)
2) если х0 – точка минимума, то ymin = f(x0)

10. Теорема Вейерштрасса

11. Экстремальные задачи

Экстремальные задачи – это задачи на поиск оптимального
(наилучшего, самого выгодного, наибольшего и т.п.) значения.
План решения:
1. Составление математической модели
Проанализировав условия задачи, выделяем оптимизируемую величину т. е.
величину, о наибольшем или наименьшем значении которой идёт речь.
Обозначаем её буквой у. Одну из участвующих в задаче неизвестных
величин, через которую сравнительно нетрудно выразить у, принимаем за
независимую переменную х. Устанавливаем реальные границы изменения х,
т. е. область определения для искомой величины у. Исходя из условий задачи
выражаем у через х. Математическая модель задачи представляет собой
функцию у = f(x) с найденной областью определения.
2. Работа с составленной моделью
В зависимости от того, что требуется в условии задачи ищем наименьшее
или наибольшее значение функции у = f(x) на отрезке [a;b], либо на
интервале (a;b).
3. Запись ответа

12. Экстремальные задачи

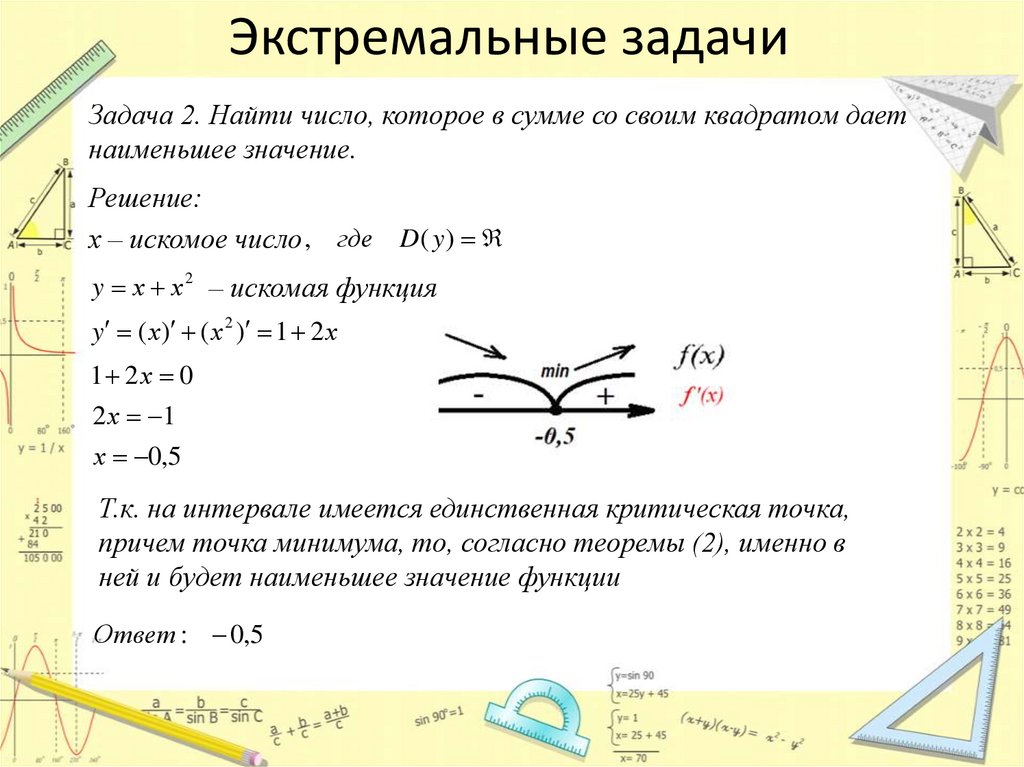
Задача 2. Найти число, которое в сумме со своим квадратом дает
наименьшее значение.
Решение:
х – искомое число , где D( y )
y х х 2 – искомая функция
y ( х) ( х 2 ) 1 2 х
1 2х 0
2 х 1
х 0,5
Т.к. на интервале имеется единственная критическая точка,
причем точка минимума, то, согласно теоремы (2), именно в
ней и будет наименьшее значение функции
Ответ : 0,5

13. Экстремальные задачи

Задача 3. Имеется бревно цилиндрической формы диаметром 30см. Из
него требуется изготовить брус прямоугольного сечения, так чтобы
количество отходов было минимальным. Определите размеры сечения
бруса.
Решение:
Количество отходов будет минимальным, если
площадь сечения наибольшая, а это возможно, когда
прямоугольник вписан в окружность (см. рис.)
2
Пусть х – ширина искомого сечения, где D (t y ) 900
(0 ; x30
) t 2 x
f ( x) прямоугольника:
900 x
По т.Пифагора выразим высоту
f (t ) t
x 2 h 2 30 2 h 2 900 x 2 h 900 x 2
2
f ( x)
1
* ( 2 x)
1
f (t )
1
2 t
* ( 2 x)
Искомая функция (площадь прямоугольника)
примет
вид:
2 у х 900 x
2 t
2 900 x
1
у ( х) 900 x 2 х( 900 x 2 ) 900 x 2 х *
* ( 2 х)
2
2 900 x
х2
900 x 2 х 2 900 2 x 2
2
900 x
2
2
900 x
900 x
900 x 2
2

14. Экстремальные задачи

Задача 3. Имеется бревно цилиндрической формы диаметром 30см. Из
него требуется изготовить брус прямоугольного сечения, так чтобы
количество отходов было минимальным. Определите размеры сечения
бруса.
Решение (продолжение): D( y ) (0; 30) h 900 x 2
y
900 2 x 2
900 x 2
900 2 x 2
900 x 2
0 900 2 x 2 0
x 450
x 2 450
x 15 2
x 15 2 (0; 30)
По теореме (2) в найденной точке будет наибольшее значение функции
h 900 (15 2 ) 2 450 15 2
Ответ : 15 2 см 15 2 см