Функции нескольких переменных

1.

1/17
Функции нескольких переменных
Определение функции двух переменных
Графическое изображение функции двух
переменных
Частное и полное приращение функции
Частные производные функции двух
переменных
Полный дифференциал
Производная сложной функции

2.

2/17
Определение функции двух переменных (ФДП)
При изучении многих явлений приходится сталкиваться с функциями
двух и более переменных.
Если каждой паре (х; у) значений двух независимых друг от друга
переменных величин х и у из некоторой области их изменения D,
соответствует определенное значение величины z, то мы говорим,
что z есть функция двух переменных, определенная на области D.
z f ( x; y )
Совокупность пар (х; у) значений независимых переменных, при
которых определяется функция z называется областью
определения этой функции.
Область определения ФДП наглядно иллюстрируется геометрически
в виде некоторой совокупности точек на плоскости XOY

3.

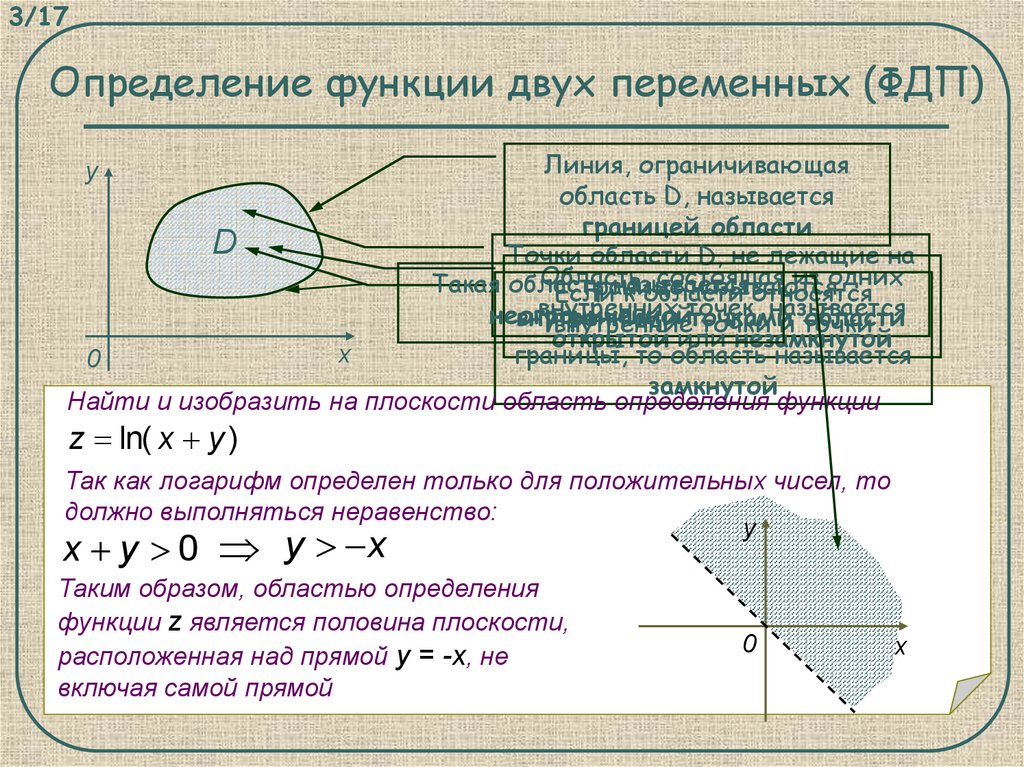
3/17
Определение функции двух переменных (ФДП)
Линия, ограничивающая
область D, называется
границей области
D
Точки области D, не лежащие на
Область,
состоящая
из одних
Такая область
называется
границе
называются
Если
к области
относятся
внутренних точек,
называется
неограниченной
внутренними
области
внутренниеточками
точки и точки
открытой или незамкнутой
x
границы, то область называется
0
замкнутой
Найти и изобразить на плоскости область определения функции
y
z ln( x y )
Так как логарифм определен только для положительных чисел, то
должно выполняться неравенство:
y
x y 0 y x
Таким образом, областью определения
функции z является половина плоскости,
расположенная над прямой y = -x, не
включая самой прямой
0
x

4.

4/17
Графическое изображение ФДП
Рассмотрим функцию z = f(x; y), определенную в области D на
плоскости XOY.
Возьмем в области D точку М(x; y),
z
Восстановим в точке М перпендикуляр к
плоскости XOY и на нем отложим
Р
расстояние, равное f(x; y)
f(x; y)
Так мы получим в пространстве точку P с
y
0
DM
x
координатами: x; y; z = f(x;y)
Геометрическое место точек Р,
координаты которых удовлетворяют
уравнению z = f(x;y), называется
графиком функции двух переменных.
Таким образом, графиком ФДП является поверхность,
проектирующаяся на плоскость XOY в область определения
функции.

5.

5/17
Частное и полное приращение функции
Рассмотрим поверхность с уравнением z = f(x; y).
Рассмотрим линию PS пересечения
поверхности с плоскостью x = const,
параллельной плоскости YOZ.
z
S
Р
Δyz
0Δy
y
Переменная z вдоль линии PS будет
меняться только в зависимости от
изменения переменной y.
Дадим переменной y приращение Δy.
x
Тогда z получит приращение , которое называется частным
приращением z по y:
y z f ( x; y y ) f ( x; y )

6.

6/17
Частное и полное приращение функции
Если пересечь поверхность плоскостью,
y = const, то вдоль линии пересечения
переменная z меняется только в
зависимости от переменной x
z
S
Δ xz
Р
x
Δx
0
y
Дадим переменной x приращение Δx ,
тогда z получит приращение , которое
называется частным приращением z
по x:
x z f ( x x; y ) f ( x; y )
Наконец, сообщив переменной x приращение Δx , а переменной y
приращение Δy, получим для z новое приращение , которое
называется полным приращением функции z :
z f ( x x; y y ) f ( x; y )

7.

7/17
Частные производные ФДП
Частной производной по х от функции z = f(x;y) называется
предел отношения частного приращения по x к приращению Δх при
стремлении Δх к нулю.
z
;
Частная производная по х обозначается одним из символов:
x
z
xz
f ( x x; y ) f ( x; y )
lim
lim
x x 0 x x 0
x
z x
Частной производной по у от функции z = f(x;y) называется
предел отношения частного приращения по у к приращению Δу при
стремлении Δу к нулю.
y z
z
f ( x; y y ) f ( x; y )
lim
lim
y
0
y
y y 0
y

8.

8/17
Частные производные ФДП
Заметив, что Δxz вычисляется при неизменном y, а Δyz при
неизменном x, можно определение частных производных
сформулировать так:
Частной производной по x от функции z называется производная,
вычисленная в предположении, что y – постоянная, частной
производной по y от функции z называется производная,
вычисленная в предположении, что x – постоянная
Вычислить частные производные от функции:
2
z
(
x
y ) x
2
ln( x y ) x
x
x2 y
2
(
y ) y
x
z
2
ln( x y ) y 2
y
x y
2x
2
x y
1
x2 y
z ln( x 2 y )

9.

9/17
Полный дифференциал ФДП
Если функция z = f(x;y) имеет непрерывные частные производные в
некоторой точке, то она дифференцируема в этой точке и имеет
полный дифференциал, определяемый выражением:
z
z
dz
x
y
x
y
Так как x; y – независимые переменные, то их приращения равны
дифференциалам: x dx; y dy
Поэтому формулу полного дифференциала можно записать в виде:
z
z
dz
dx
dy
x
y
Можно доказать, что полное приращение функции Δz и полный
дифференциал dz связаны друг с другом с помощью соотношения:
z dz 1 x 2 y

10.

10/17
Полный дифференциал ФДП
z dz 1 x 2 y
В этом выражении γ1 и γ2 - бесконечно малые функции когда Δx и Δy
стремятся к нулю.
Таким образом, полное приращение дифференцируемой функции
может быть представлено в виде полного дифференциала и
величины бесконечно малой высшего порядка относительно x 2 y 2
Поэтому, имеет место приближенная формула, которая применяется
в приближенных вычислениях:
z dz
f ( x x; y y ) f ( x; y ) dz
f ( x x; y y ) f ( x; y ) dz
(1)

11.

11/17
Полный дифференциал ФДП
3.012 4.022
2
2
Введем функцию: z x y
Вычислить приближенно:
Необходимо вычислить значение этой функции в точке (3,01; 4,02)
x 3;
x 0.01;
x x 3.01;
Тогда, согласно формуле (1):
y 4; y 0.02;
y y 4.02
z(3.01; 4.02) z(3;4) dz ( 3;4 )
z(3;4) 32 42 5
z
x
x
z
y
x
dz
3
4
0.01 0.02 0.022
5
5
2
2
y
y
2
2
x
y
x
x2 y 2
3
5
4
5
(3;4)
y
x2 y 2
(3;4)
z(3.01; 4.02)
5 0.022 5.022

12.

14/17
Производная сложной функции
Предположим, что в уравнении:
z F (u;v )
u и v являются функциями независимых переменных x и y:
u ( x; y ), v ( x; y )
В этом случае z есть сложная функция от аргументов x и y.
Предположим, что функции F (u;v ), ( x; y ), ( x; y )
имеют непрерывные частные производные по всем аргументам, тогда
частные производные функции z по переменным x и y вычисляются
по формулам:
z z u z v
x u x v x
z z u z v
y u y v y
(4)

13.

15/17
Производная сложной функции
z ln( u v ), u e
2
x y 2
, v x 2 y Вычислить частные производные
функции z по переменным x и y.
1
z
2
ln( u v ) v
u2 v
v
u
x y 2
x y 2
2y
e
y e
y
v
2
x y y 1
y
z
2u
2
ln( u v ) u 2
u
u v
u
x y 2
x y 2
e
x
e
x
v
2
x y x 2x
x
Подставим найденные производные в формулы (4):
z
z
u
yx
u
xy
z
v
v
xy

14.

16/17
Производная сложной функции
Если задана функция
где
z F (u;v )
u и v зависят только от одной переменной x , то в конечном итоге
z также является функцией одной переменной и можно ставить
вопрос о нахождении производной dz
dx
dz z du z dv
dx u dx v dx
(5)
z F ( x; y ) , где y зависит только от x: y f (x )
Тогда, для нахождения производной dz
dx используют формулу:
В частном случае
dz z z dy
dx x y dx
(6)

15.

17/17
Производная сложной функции
z x2 y ,
y sin x
Вычислить производную функции z по x.
Подставим найденные производные в формулу (6):
dz
dx
z
x
z
y
1
z
2
x y y
2 y
y
z
2
x y x 2x
x
dy
sin x cos x
dx
dy
dx