Перевод чисел в различные системы счисления

1. Перевод чисел в различные системы счисления

ПЕРЕВОД ЧИСЕЛ В РАЗЛИЧНЫЕ
СИСТЕМЫ СЧИСЛЕНИЯ

2.

3.

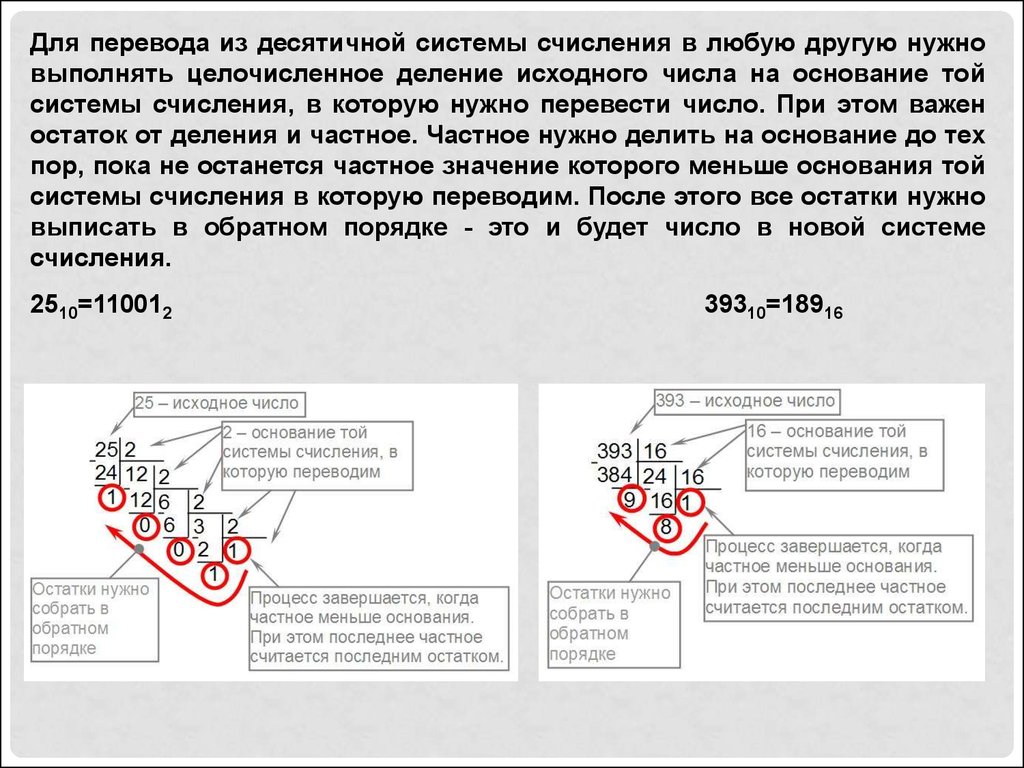
Для перевода из десятичной системы счисления в любую другую нужно
выполнять целочисленное деление исходного числа на основание той
системы счисления, в которую нужно перевести число. При этом важен
остаток от деления и частное. Частное нужно делить на основание до тех
пор, пока не останется частное значение которого меньше основания той
системы счисления в которую переводим. После этого все остатки нужно
выписать в обратном порядке - это и будет число в новой системе
счисления.
2510=110012
39310=18916

4.

Для перевода в десятичную систему счисления необходимо
расставить разряды справа налево начиная с 0. Число которое
переводим представить в виде многочлена, состоящего из
произведений цифр числа на основание системы счисления в той
степени в каком разряде находится данная цифра, и вычислить по
правилам десятичной арифметики.
101012 = 1×24 + 0×23 + 1×22 + 0×21 + 1×20 =
= 16+0+4+0+1=2110
2168 = 2×82 + 1×81 +6×80 = 128+8+6 = 14210

5.

6.

Чтобы перевести число из двоичной системы в восьмеричную, его
нужно разбить на триады (тройки цифр), начиная с младшего разряда, в
случае необходимости дополнив старшую триаду нулями, и каждую
триаду заменить на соответствующее десятичное число.
11101012 = 5618
1012 = 1×22 + 0×21 + 1×20 = 5
1102 = 1×22 + 1×21 + 0×20 = 6
0012 = 0×22 + 0×21 + 1×20 =1
Для перевода восьмеричного числа в двоичное необходимо каждую
цифру заменить эквивалентной ей двоичной триадой.

7.

Чтобы перевести число из двоичной системы в шестнадцатеричную, его
нужно разбить на тетрады (четверки цифр), начиная с младшего разряда,
в случае необходимости дополнив старшую тетрады нулями, и каждую
тетраду заменить на соответствующее десятичное число.
11111012 = D716
11012 = 1×23 + 1×22 + 0×21 + 1×20 = 13 (D)
01112 = 0×23 + 1×22 + 1×21 + 1×20 = 7
Для перевода шестнадцатеричного числа в двоичное необходимо
каждую цифру заменить эквивалентной ей двоичной тетрадой.