Similar presentations:
Математика. Профильный уровень. ЕГЭ
1.
2.
• ЕГЭ по математике является обязательнымэкзаменом любого школьника в 11 классе.
• Экзамен по математике делится на два
вида - базовый и профильный
• Задания ЕГЭ строго тематические,
поэтому для каждого номера можно дать
точные рекомендации и привести теорию,
необходимую именно для решения
данного вида задания.
3.
Структура профильного уровня ЕГЭ поматематике
Экзаменационная работа состоит из двух частей,
которые различаются по содержанию, сложности и
числу заданий:
• 8 заданий первой части (задания 1–8) с кратким ответом
в виде целого числа или конечной десятичной дроби
• 4 задания второй части (задания 9–12) с кратким
ответом в виде целого числа или конечной десятичной
дроби
• 7 заданий второй части (задания 13–19) с развернутым
ответом (полная запись решения с обоснованием
выполненных действий)
4.
По уровню сложности задания распределяютсяследующим образом:
• Задания первой части направлены на проверку освоения базовых
умений и практических навыков применения математических знаний в
повседневных ситуациях.
• Посредством заданий второй части осуществляется проверка освоения
математики на профильном уровне, необходимом для применения
математики в профессиональной деятельности и на творческом уровне.
• задания 1–8 имеют базовый уровень
• задания 9–17 – повышенный уровень
• задания 18 и 19 относятся к высокому уровню сложности
! При выполнении заданий с развернутым ответом части 2
экзаменационной работы в бланке ответов № 2 должны быть
записаны полное обоснованное решение и ответ для каждой задачи.
5.
Рекомендуемая таблица перевода первичныхбаллов в стобальную систему
Номера
заданий
Макс.
количество
первичных
баллов
Количество
решенных
заданий
Максимальное
количество
первичных баллов
Максимальн.
итоговый
балл
12
12
62
1-12
1
13
14
70
13-15
2
14
16
74
16-17
3
18-19
4
15
18
78
16
21
84
17
24
90
18
28
98
19
32
100
6.
Популярные ошибки в ЕГЭ поматематике
• Задачи на проценты – непонимание механизма начисления
процентов
• Невнимательное чтение условия
• Непонимание текста задачи
• Вычислительные ошибки
• Ошибки в теоретических фактах
• Незнание алгоритмов и методов решения
• Неверное чтение чертежей, непонимание элементов геометрии,
ошибки в построении чертежа
• Неумение доказывать, обосновывать
• Задания по тригонометрии требуют тщательности решения
• Отсутствие навыков математического моделирования
7.
Примеры заданий из экзаменовпрошлых лет
8.
4. Задача про ковбоя ДжонаКовбой Джон попадает в муху на стене с
вероятностью
0,8,
если
стреляет
из
пристрелянного револьвера. Если Джон стреляет
из непристрелянного револьвера, то он попадает
в муху с вероятностью 0,2.
На столе лежат 10 револьверов, из них только 2
пристрелянных. Он хватает первый попавшийся
револьвер и стреляет в муху. Найти вероятность
того, что Джон промахнется.
• Согласно теореме умножения вероятностей , вероятность того, что ковбой Джон
взял пристрелянный револьвер и при этом промахнулся равна
Р1=(1-0,8) *2/10=0,04
• Вероятность того, что взят непристрелянный револьвер и при этом промахнулся
равна
Р2=(1-0,2)*8/10=0,64
• Согласно теореме сложения вероятностей, ищем вероятность промаха любым
револьвером
Р= Р1+Р2= 0,04+0,64=0,68
9.
Задачи с элементами комбинаторики.В соревнованиях участвуют 6 команд А, В, С, D, Е , F. Сколько существует
вариантов расположения команд с первого по шестое место, где команда
А ни на первом, ни на последнем месте.
Перестановки .
Вычисляя перестановки, определяем, сколькими различными способами
можно переупорядочить элементы множества, не меняя их количество.
Pn = n!
Решение
* Вычислим все возможные варианты построения команд – то есть число перестановок
6 команд по 6 местам
Р6=6!=1*2*3*4*5*6=720
* Вычислим все возможные варианты, где команда А не на 1 месте ( то есть на 2,3,4,5,6
месте)
Р5= 5!= 1*2*3*4*5 = 120
* Аналогичное число вариантов будет, если команда А не на последнем месте ( то есть на
1,2,3,4,5 месте)
Р5=5!=1*2*3*4*5=120
* Найдем число расположений команды А без 1 и последнего места
Р=720-120-120=480 способов
10.
14. СтереометрияВ правильной треугольной призме АВСА1В1С1 все ребра равны корень
из 13.
А) Докажите, что СD перпендикулярна DN, если D и N середины ребер ВВ1
и В1А1
Б) Найдите угол между плоскостями CDN и BCC1
11.
12.
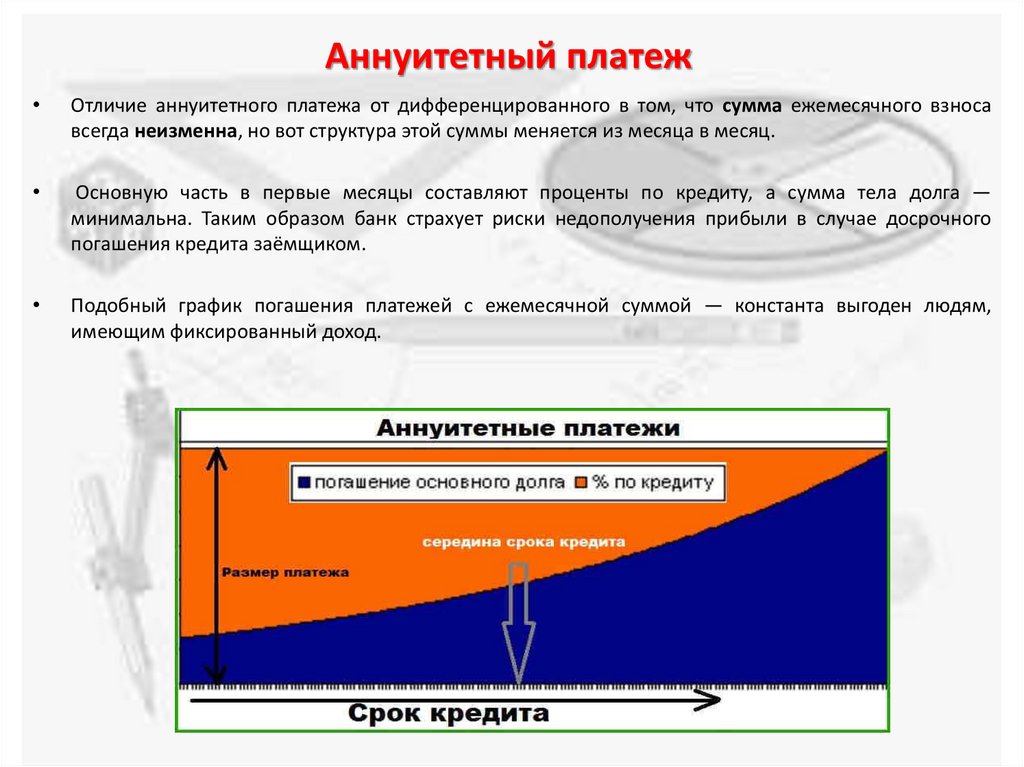
Аннуитетный платежОтличие аннуитетного платежа от дифференцированного в том, что сумма ежемесячного взноса
всегда неизменна, но вот структура этой суммы меняется из месяца в месяц.
Основную часть в первые месяцы составляют проценты по кредиту, а сумма тела долга —
минимальна. Таким образом банк страхует риски недополучения прибыли в случае досрочного
погашения кредита заёмщиком.
Подобный график погашения платежей с ежемесячной суммой — константа выгоден людям,
имеющим фиксированный доход.
13.
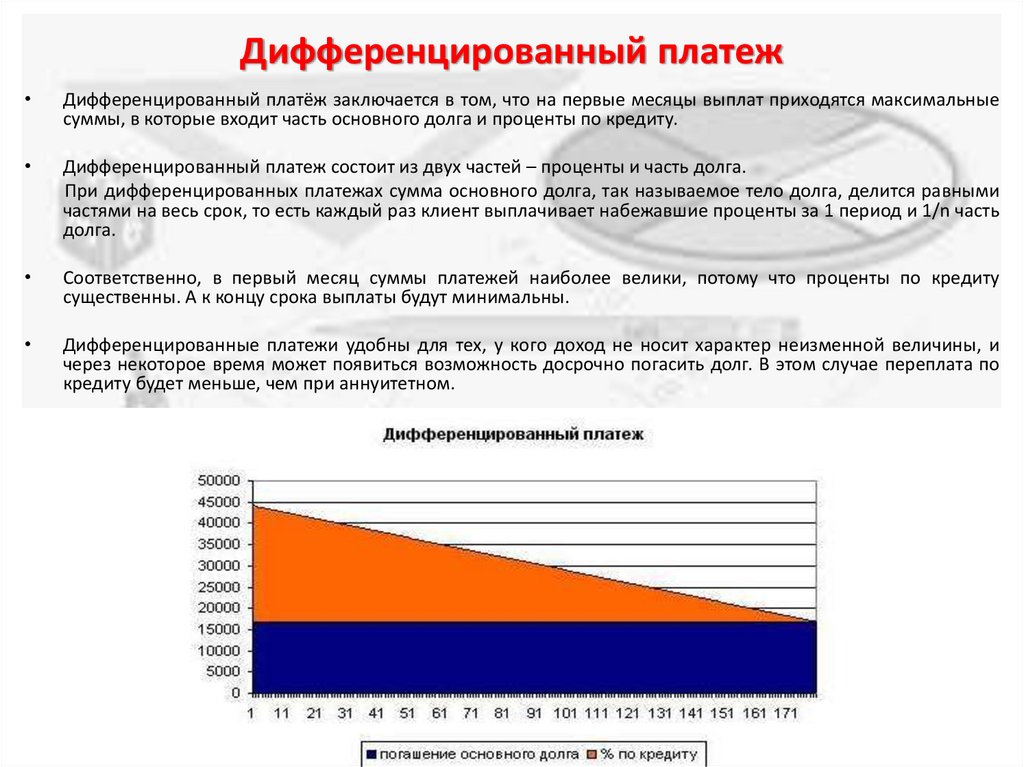
Дифференцированный платежДифференцированный платёж заключается в том, что на первые месяцы выплат приходятся максимальные
суммы, в которые входит часть основного долга и проценты по кредиту.
Дифференцированный платеж состоит из двух частей – проценты и часть долга.
При дифференцированных платежах сумма основного долга, так называемое тело долга, делится равными
частями на весь срок, то есть каждый раз клиент выплачивает набежавшие проценты за 1 период и 1/n часть
долга.
Соответственно, в первый месяц суммы платежей наиболее велики, потому что проценты по кредиту
существенны. А к концу срока выплаты будут минимальны.
Дифференцированные платежи удобны для тех, у кого доход не носит характер неизменной величины, и
через некоторое время может появиться возможность досрочно погасить долг. В этом случае переплата по
кредиту будет меньше, чем при аннуитетном.
14.
Основные формулыАннуитетный платеж
• П = С*( ПР / 1-(1+ПСМ) – СП )
П- аннуитетный платеж;
ПР - процентная ставка,
установленная на период
начисления;
С - первоначальная сумма кредита;
СП - количество периодов (в
месяцах);
ПСМ - это ежемесячная
процентная
ставка или
1/12 годовой.
Дифференцированн
ый платеж
НП= СК*ПС*(КП+1)/2
НП – начисленные проценты;
СК – сумма кредита;
ПС – гдоовая проц. ставка
КП – количество периодов
15.
Как определить к какому виду платежей относитсязадача?
Аннуитетный платеж
Ключевая фраза
• «Выплаты производятся равными
платежами»
• «Второй платеж в 2 раза больше
первого, третий в 3 раза больше
второго»
Дифференцированный
платеж
Ключевая фраза
• «Сумма долга понижается
равномерно»
• Дана таблица изменения суммы
долга
• «Долг уменьшился на 1 и ту же
величину»
16.
Аннуитетный платежВ июле планируется взять кредит на сумму 69510 рублей.
Условия его возврата таковы:
- Каждый январь долг возрастает на 10% по сравнению с концом
предыдущего года
- С февраля по июнь каждого года необходимо выплатить некоторую часть
долга
На сколько рублей больше придется отдать в случае, если кредит будет
полностью погашен тремя равными платежами (то есть за три года) по
сравнению со случаем, если кредит будет полностью погашен двумя
равными платежами (то есть за два года)?
17.
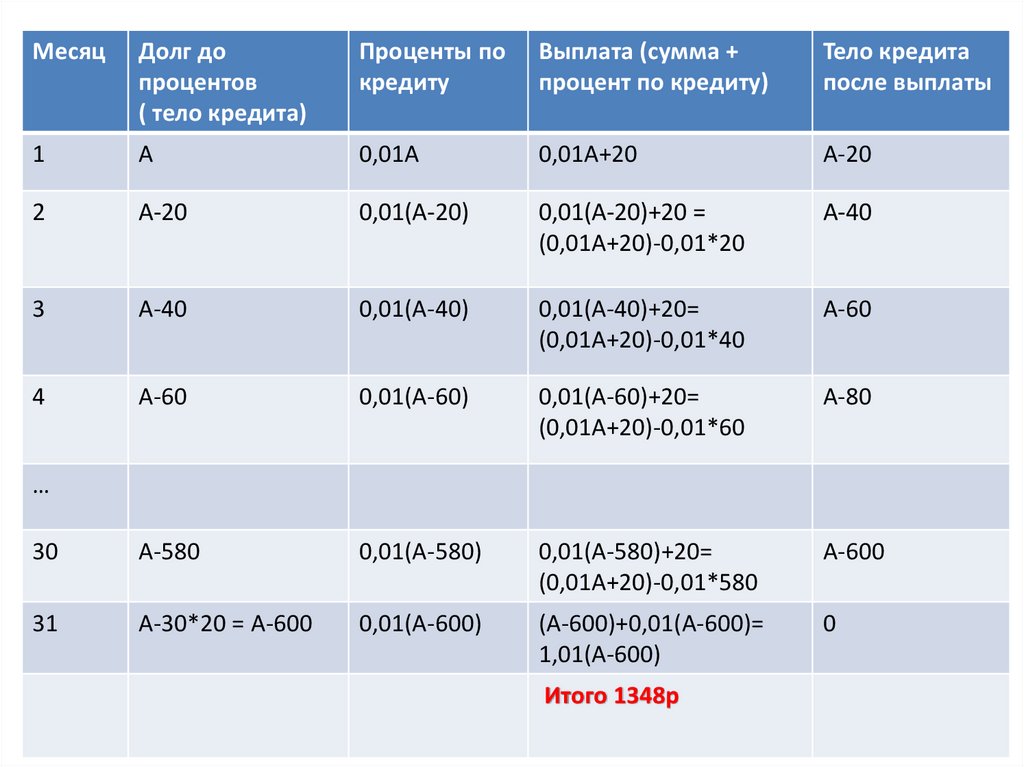
Дифференцированный платеж15-го января планируется взять кредит в банке на некоторую сумму на 31
месяц.
Условия его возврата таковы:
- 1 числа каждого месяца долг увеличивается на 1% по сравнению с
концом предыдущего месяца
- Со 2 по 14 число каждого месяца необходимо выплатить одним
платежом часть долга
- На 15 число каждого месяца с 1 по 30 –й , долг должен быть на 20 тыс.
рублей меньше долга на 15 число предыдущего месяца
- К 15 числу 31 месяца долг должен быть погашен полностью.
Сколько тысяч рублей составляет долг на 15 число 30-го месяц, если банку
всего было выплачено 1348000 рублей?
18.
МесяцДолг до
процентов
( тело кредита)
Проценты по
кредиту
Выплата (сумма +
процент по кредиту)
Тело кредита
после выплаты
1
А
0,01А
0,01А+20
А-20
2
А-20
0,01(А-20)
0,01(А-20)+20 =
(0,01А+20)-0,01*20
А-40
3
А-40
0,01(А-40)
0,01(А-40)+20=
(0,01А+20)-0,01*40
А-60
4
А-60
0,01(А-60)
0,01(А-60)+20=
(0,01А+20)-0,01*60
А-80
30
А-580
0,01(А-580)
0,01(А-580)+20=
(0,01А+20)-0,01*580
А-600
31
А-30*20 = А-600
0,01(А-600)
(А-600)+0,01(А-600)=
1,01(А-600)
0
…
Итого 1348р
19.
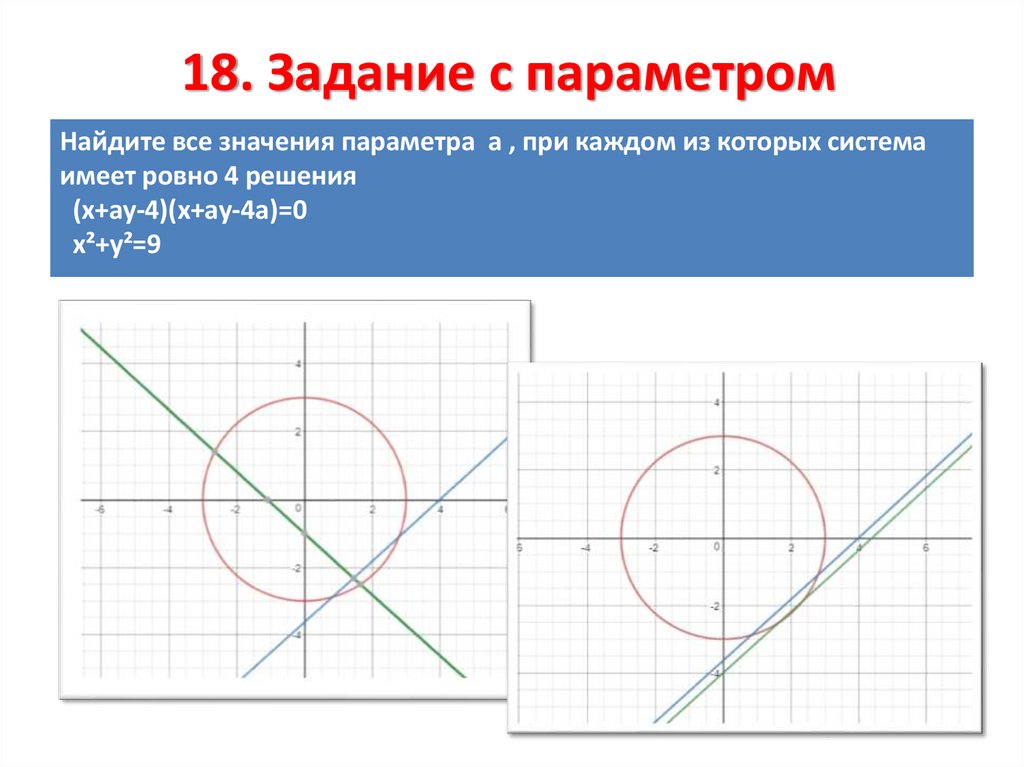
18. Задание с параметромНайдите все значения параметра а , при каждом из которых система
имеет ровно 4 решения
(х+ау-4)(х+ау-4а)=0
х²+у²=9
20.
Спасибо за внимание,жду вас на занятиях.
















 mathematics
mathematics








