Similar presentations:
Последовательности
1.
Последовательности.2.
1. Какие события в нашей жизни происходят последовательно?Приведите примеры таких явлений и событий.
- дни недели,
- названия месяцев,
- возраст человека,
- номер счёта в банке,
- последовательно происходит смена дня и ночи,
- последовательно увеличивает скорость автомобиль, и т. д.
2. Что такое последовательность?
Числовая последовательность – это функция,
заданная на множестве натуральных чисел.
Вывод:
Числовая последовательность
1) функция
2) ее область определения – множество N.
3.
№3№1
№5
№9
№7
Последовательность нечетных чисел: 1, 3, 5, 7, 9, 11, …
№2
№4
№6
№8
№10
Последовательность четных чисел: 2, 4, 6, 8, 10, 12, …
Последовательность считается заданной, если указан
закон, по которому каждому натуральному числу n
ставится в соответствие элемент xn некоторого
множества.
4.
Последовательность квадратов чисел натурального ряда:1, 4, 9, 16, 25, 36, 49, 64,…
Последовательность простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …
Последовательность чисел, обратных натуральным:
1, 1 , 1 , 1 , 1 , 1 , ...
2 3 4 5 6
Последовательность степеней двойки:
1, 2, 4, 8, 16, 32, 64, 128, 256, …
Последовательность десятичных приближений к числу :
3,1; 3,14; 3,141; 3,1415; 3,14159; …
5.
Числа, образующие последовательность, называютсячленами последовательности.
Члены последовательности обозначают буквами с
индексами, указывающими порядковый номер члена.
Пример: (an ) : a1 , a2 , a3 , a4 ,...an .
Читают: «a первое, а второе, а третье, а четвертое» и т.д.
a n − член последовательности с номером n
читают: «n – й член последовательности».
Саму последовательность обозначают: ( an )
Последовательности
Бесконечные
(an ) : a1 , a2 , a3 , a4 ,...an ...
Конечные
(bn ) : b1 , b2 , b3 , b4 ,...bn
6.
• Какие последовательности будутконечными?
• Приведите примеры конечных числовых
последовательностей.
• Какие последовательности будут
бесконечными?
• Приведите примеры бесконечных числовых
последовательностей.
7.
№563 (устно)Какой член последовательности а1 , а2 ,а 3 ,... :
а) следует за членом а99 , а200 ,а n , an 1 , an 1 , a2 n ;
б) предшествует члену а71, а100 ,а n 2 , an 3 , a3n ?
№564 (устно)
Перечислите члены последовательности x n , которые
расположены между:
а) x31 и x35 ;
б ) xn и xn 6 ;
г) xn 2 и xn 2 .
в) xn 4 и xn ;
8.
• Аналитический• Рекуррентный
• Графический
• Описательный (словесный)
• Табличный
9.
АналитическийПоследовательность задают с помощью
формулы n – го члена последовательности.
Пример 1. Последовательность чётных чисел: xn 2n.
x1 2, x2 4, x3 6, x4 8, x10 20, x100 200...
Пример 2. Последовательность квадрата натуральных
2
чисел: y n n .
y1 1, y2 4, y3 9, y4 16, y10 100, y100 10000...
Пример 3. Стационарная последовательность: сn С.
с1 С, с2 С, с3 С, с4 С, с10 С, с100 С...
Любой n-й член последовательности можно определить с
помощью формулы.
10.
Найдите первые шесть членов последовательности,заданной формулой n – го члена:
n
а) xn 2n 1;
б ) xn
;
n 1
Решение :
Решение :
x1 2 1 1 2 1 1;
4
4
1
1
x4
;
x
;
1
x2 2 2 1 4 1 3;
4 1 5
1 1 2
x3 2 3 1 6 1 5;
5
5
2
2
;
x2
; x5
x4 2 4 1 8 1 7;
5 1 6
2 1 3
x5 2 5 1 10 1 9;
3
3
6
6
x3
; x6
.
x6 2 6 1 12 1 11.
3 1 4
6 1 7
xn : 1;3;5;7;9;11...
1 2 3 4 5 6
xn : ; ; ; ; ; ...
2 3 4 5 6 7
11.
Найдите первые шесть членов последовательности,заданной формулой n – го члена:
д) xn 2n 3 ;
Решение :
12.
Какой формулой задается последовательность?1 1 1 1
1) xn : 1; ; ; ; ...
2 3 4 5
Решение :
1
x7 .
1
xn .
7
n
2) an : 1;2;4;8;16;...128;...
( Последовательность степеней двойки )
Решение :
7 1
6
n 1
a
2
2
64.
7
an 2 .
Найдите седьмой член этих последовательностей?
13.
Числовая последовательность задана формулойxn 2n 3. Найти номер члена последовательности,
равного 43; 50.
Решение :
Решение :
б ) xn 50;
а) xn 43;
2n 3 50;
2n 3 43;
2n 50 3;
2n 43 3;
2n 47;
2n 40;
n 47 : 2;
n 40 : 2;
n 23,5.
n 20.
n N , значит в данной
n N , значит x20 43.
последовательности нет члена,
Ответ : n 20.
равного 50.
14.
Рекуррентный(от латинского слова recurro − возвращаться)
Задают несколько первых членов последовательности
и правило, позволяющее вычислять каждый
следующий член через предыдущий.
Пример 1
а) а1 6, аn 1 an 2.
б ) а1 1, а2 2, an 1 an 1 an 1 , n 2 .
15.
Пример 1Найдите первые пять членов последовательности, если:
а) а1 6, аn 1 an 2. б )а1 1, а2 2, an 1 an 1 an 1 ,
Решение :
n 2 .
а1 6;
Решение :
а2 a1 2 6 2 4;
а3 a2 2 4 2 2;
а4 a3 2 2 2 0;
а5 a4 2 0 2 2.
Ответ : an : 6;4;2;0; 2...
а1 1;
а2 2;
а3 a2 1 a1 2 1 1 4;
а4 a3 1 a2 4 1 2 7;
а5 a4 1 a3 7 1 4 12;
Ответ : an : 1;2;4;7;12...
Вывод: Для рекуррентного задания последовательности необходимо:
1) знать один или два первых члена последовательности
2) указать правило для вычисления следующих членов последовательности
16.
Найдите первые пять членов последовательности,если:
1
а) а1 1, аn 1 an 1
г ) а1 3, аn 1 an
Решение :
Решение :
17.
ОписательныйПравила задания последовательности описываются
словами, без указания формул или когда
закономерности между элементами нет.
Пример 1. Последовательность простых чисел:
xn : 2; 3; 5; 7; 11; 13; 17; 19; 23;...
Пример 2. Последовательность натуральных четных
чисел:
yn : 2; 4; 6; 8; 10; 12; 14; 16; 18;...
Пример 3. Последовательность натуральных чисел,
кратных 7: cn : 7; 14; 21; 28; 35; 42; 49; 56; 63;...
18.
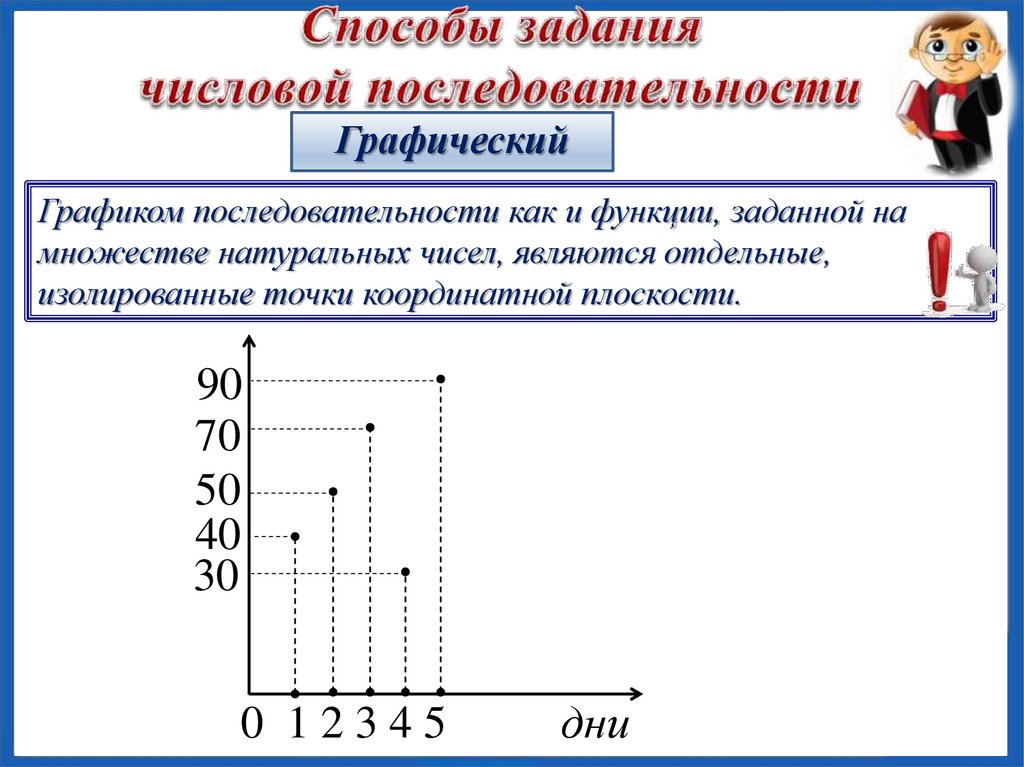
ГрафическийГрафиком последовательности как и функции, заданной на
множестве натуральных чисел, являются отдельные,
изолированные точки координатной плоскости.
90
70
50
40
30
0 12345
дни
19.
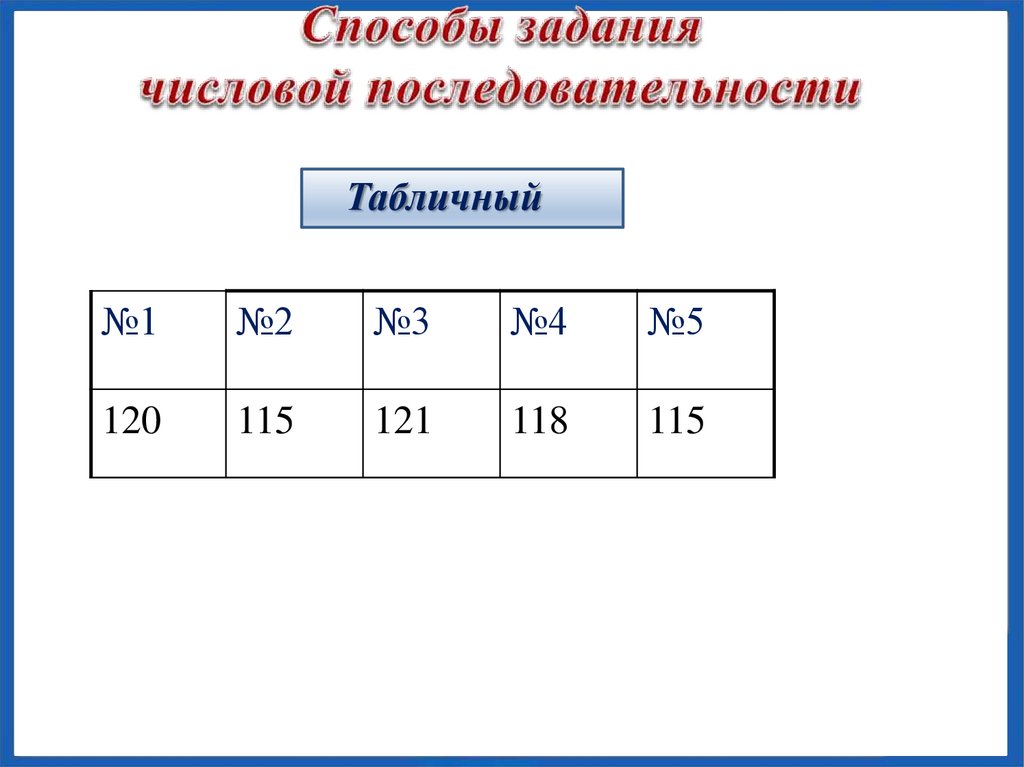
Табличный№1
№2
№3
№4
№5
120
115
121
118
115
20.
1) Является ли конечной или бесконечной последовательностьчисел :
а)делители числа 1200 ?
б )кратных числа 8 ?
а)делители числа 2400 ?
б )кратных числа 6 ?
2) Последовательность задана формулой
an 5n 2
bn n 2 3
Чему равен ее третий
У8844 член ?
3) Запишите последний член последовательности
всех трехзначных чисел.
всех двузначных чисел.
4) Дана рекуррентная формула последовательности
a1 5, an 1 an 4.
bn
b1 8, bn 1 .
4
Выпишите первые пятьт членов последовательности.
21.
1) Что называется числовой последовательностью?2) Приведите примеры конечной числовой
последовательности?
3) Приведите примеры бесконечной числовой
последовательности?
4) Что такое n – член последовательности?
5) Что такое формула n – го члена
последовательности?
6) Какие способы задания последовательности
изучили?
7) В чем заключается рекуррентный способ задания
последовательности?


















 mathematics
mathematics








