векторы

1.

Векторы в пространстве
вход

2.

Содержание
I.
II.
III.
IV.
V.
VI.
Понятие вектора в пространстве
Коллинеарные векторы
Компланарные векторы
Действия с векторами
Разложение вектора
Базисные задачи
Проверь себя
Об авторе
Помощь в управлении презентацией
Выход

3.

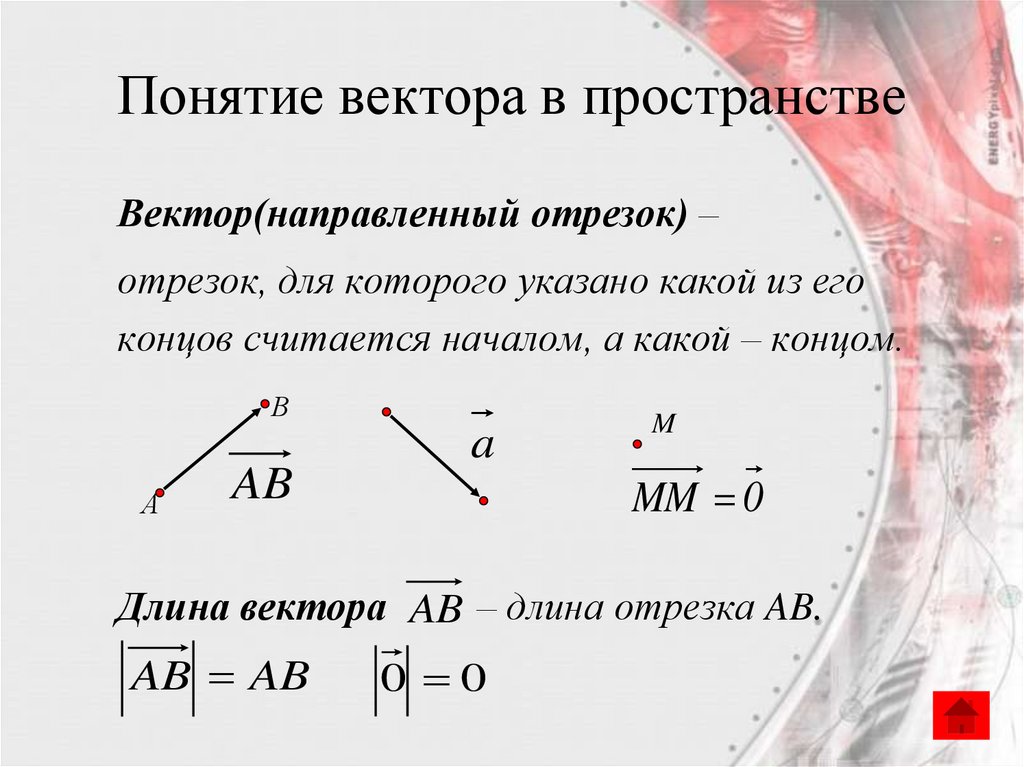
Понятие вектора в пространстве
Вектор(направленный отрезок) –
отрезок, для которого указано какой из его
концов считается началом, а какой – концом.
В
А
AB
a
M
MM 0
Длина вектора AB – длина отрезка AB.
AB AB
0 0

4.

Коллинеарные векторы
Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или параллельных прямых.
Среди коллинеарных различают:
• Сонаправленные векторы
• Противоположно направленные векторы

5.

Сонаправленные векторы
Сонаправленные векторы - векторы, лежащие
по одну сторону от прямой, проходящей через их
начала.
a
a b
b
Нулевой вектор считается сонаправленным с
любым вектором.
• Равные векторы

6.

Равные векторы
Равные векторы - сонаправленные векторы,
длины которых равны.
a
a b a b, a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.

7.

Противоположно направленные
векторы
Противоположно направленные векторы –
векторы, лежащие по разные стороны от прямой,
проходящей через их начала.
a
a b
b
Противоположные векторы

8.

Противоположные векторы
Противоположные векторы – противоположно
направленные векторы, длины которых равны.
a
a b a b, a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.

9.

Признак коллинеарности
Если существует такое число k при котором
выполняется равенство a k b и при том
вектор b 0 , то векторы a и b коллинеарн ы.
Доказательство

10.

Определение компланарных
векторов
Компланарные векторы – векторы, при
откладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.
Пример:
B1
A1
C1
D1
B
А
C
D
BB1 , AC,AC 1 компланарн ы, т.к.
BB1 AA1 , а векторы AA1 , AC , AC1
лежат в плоскости (AA1C)

11.

О компланарных векторах
Любые два вектора всегда компланарны.
α
a
b
a
b
a
b
a и b компланарн ы
Три вектора, среди которых имеются два
коллинеарных, компланарны.
a, b и c
компланарны
если
a , b, c
a kb

12.

Признак компланарности
Если вектор c можно разложить по векторам
а и b, т.е. представить в виде
с xa yb
где х и у некоторые числа, то векторы a, b
и c компланарн ы.
Доказательство
Задачи

13.

Свойство компланарных
векторов
Если векторы a, b и c компланарн ы, то один из них
можно выразить линейным образом через два других,
т.е. представить в виде :
с xa yb
причем коэффициен ты разложения
определяют ся единственным образом.

14.

Действия с векторами
Сложение
Вычитание
Умножение вектора на число
Скалярное произведение

15.

Сложение векторов
Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
Свойства сложения

16.

Правило треугольника
Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А вектор
AB, равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
А
b
a b
b
C

17.

Правило треугольника
B
a
А
a b
b
C
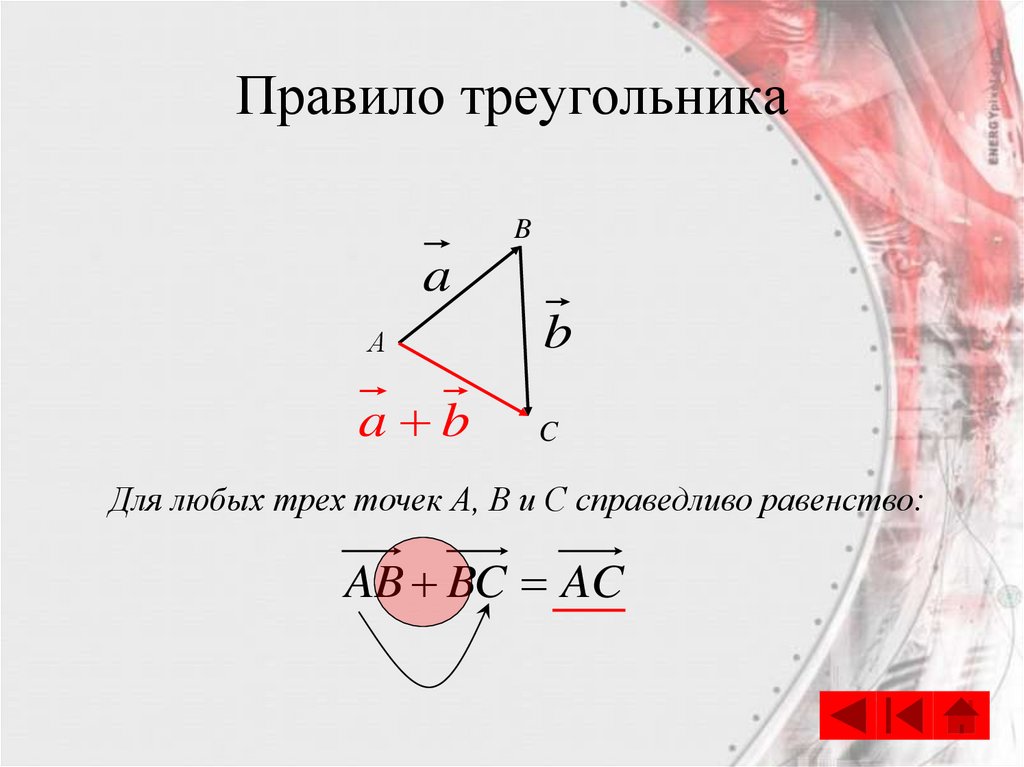
Для любых трех точек А, В и С справедливо равенство:
AB BC AC

18.

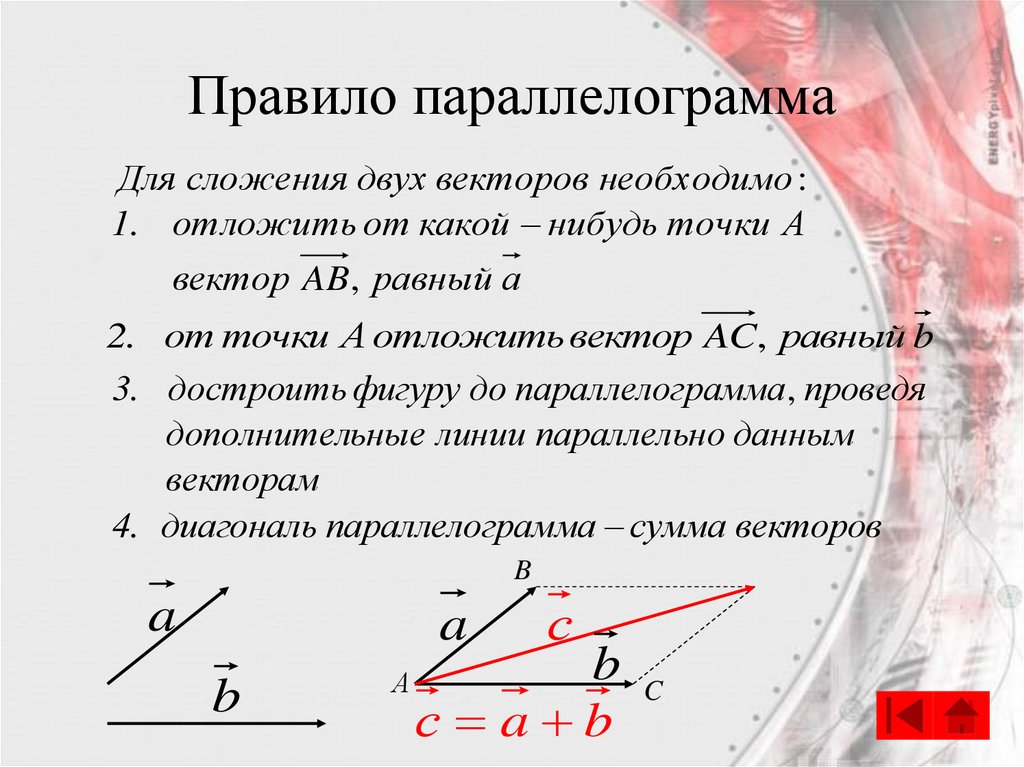
Правило параллелограмма
Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC, равный b
3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b
с a b
C

19.

Свойства сложения
Для любых векторов a , b и c справедливы
равенства :
a b b a
a b с а b с
переместительный закон
сочетательный закон

20.

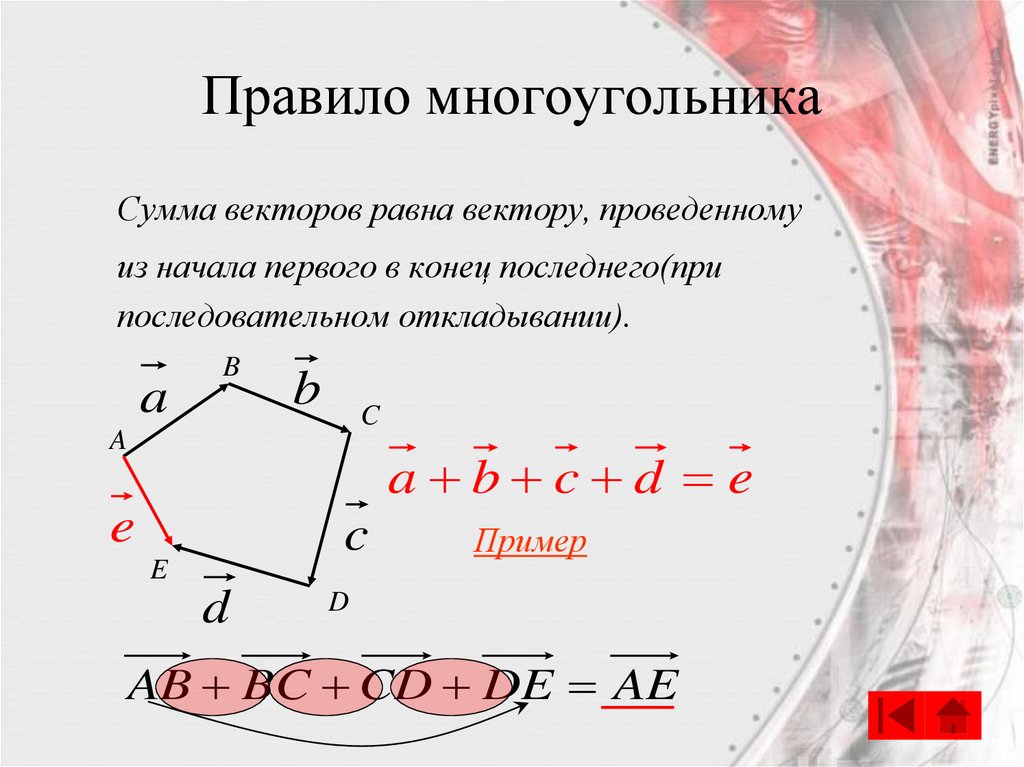
Правило многоугольника
Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE

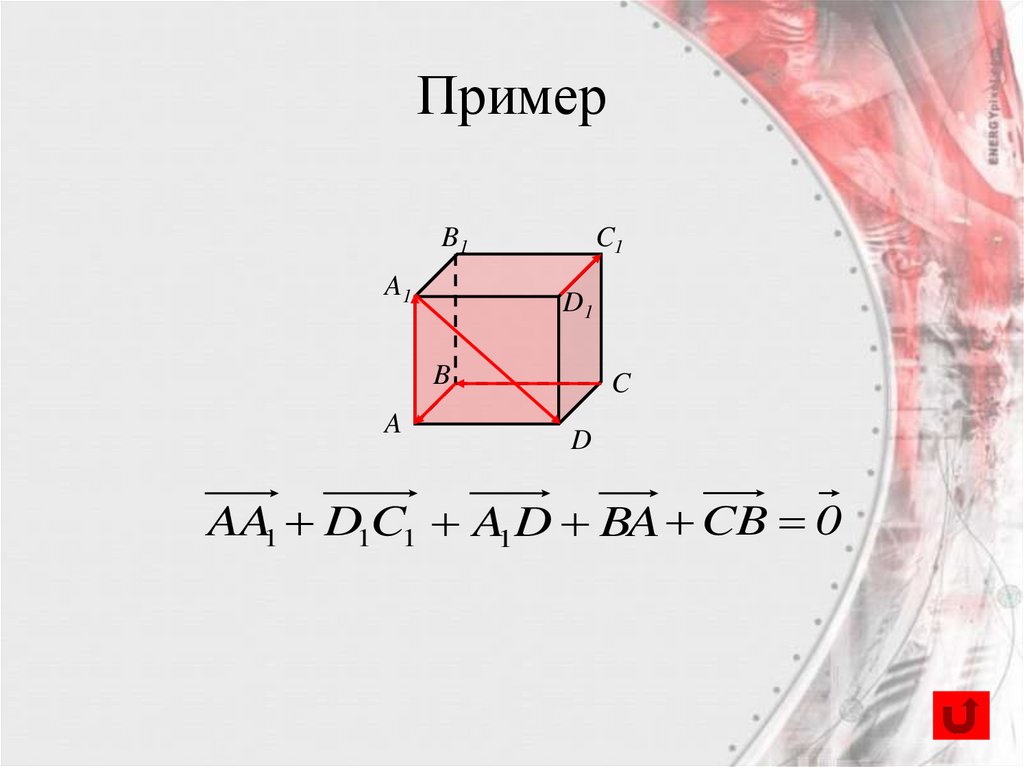
21.

Пример
B1
A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0

22.

Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1
C1
1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d

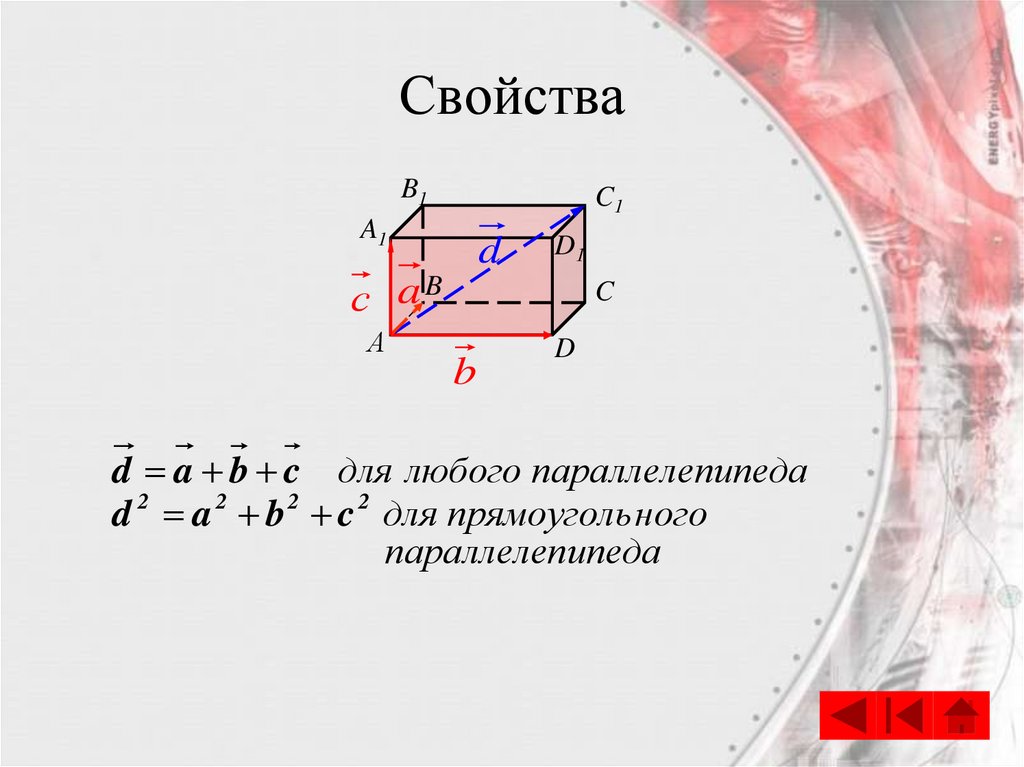
23.

Свойства
B1
C1
A1
d
D1
с aB
А
C
b
D
d a b c для любого параллелепипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелепипеда

24.

Вычитание векторов
• Вычитание
• Сложение с противоположным

25.

Вычитание
Разностью векторов a и b называется такой
вектор, сумма которого с вектором b равна
вектору a .

26.

Вычитание
Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
Правило трех точек
a
a b
A
b
C

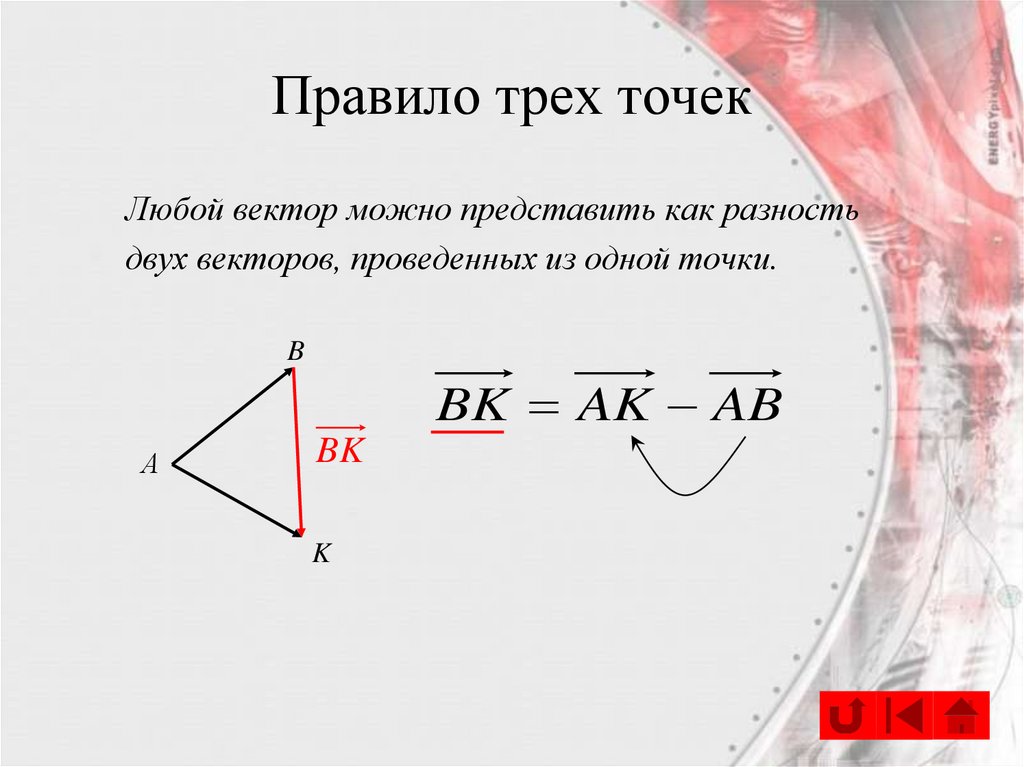
27.

Правило трех точек
Любой вектор можно представить как разность
двух векторов, проведенных из одной точки.
B
BK AK AB
А
BK
K

28.

Сложение с противоположным
Разность векторов
как сумму вектора
a
a
и
b можно представить
и вектора,
противоположного вектору
b.
a b a b
a
B
b
a b
b
O
А
a

29.

Умножение вектора на число
Произведением ненулевог о вектора a на число k
называется такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3

30.

Свойства
• Произведением нулевого вектора на любое число
считается нулевой вектор.
0 n 0
• Произведение любого вектора на число нуль есть
нулевой вектор.
n 0 0

31.

Свойства
Для любыхвект оровa и b и любых
чисел k, l справедливы равенст ва:
(kl)a k(la )
сочет ат ельный закон
k( a b ) k a k b
1 ый распределит ельный
закон
(k l)a k a l a
2 ой распределит ельный
закон

32.

Скалярное произведение
Скалярным произведением двух векторов
называется произведение их длин на косинус угла
между ними.
ab a b cos( a ; b )
Справедливые утверждения
Вычисление скалярного произведения в координатах
Свойства скалярного произведения

33.

Справедливые утверждения
• скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны
a b 0 a 0 b 0 a b
• скалярный квадрат вектора (т.е. скалярное
произведение вектора на себя) равен квадрату
его длины
2
a
а
2
а
2

34.

Вычисление скалярного
произведения в координатах
Скалярное произведен ие векторов a x1 ; y1 ; z1
и b x 2 ; y 2 ; z 2 выражается формулой
a b x 1 x 2 y1 y 2 z 1 z 2
Доказательство

35.

Свойства скалярного
произведения
Для любых векторов a , b и с и любого
числа k справедливы равенства :
10.
2
a 0 причем a 0 при a 0
20. a b ba (переместительный закон)
(распределительный
0
a
b
c
a
c
b
c
3.
закон)
40. k a b k a b (сочетательный закон)

36.

Разложение вектора
• По двум неколлинеарным векторам
• По трем некомпланарным векторам

37.

Разложение вектора по двум
неколлинеарным векторам
Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.
Доказательство

38.

Разложение вектора по трем
некомпланарным векторам
Если вектор p представлен в виде
p xa yb z c
где x, y, z – некоторые числа, то говорят, что вектор
p разложен по векторам a , b и c .
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
Доказательство

39.

Определение. Векторным произведением двух
ненулевых векторов a и b называется вектор c ,
для которого выполняются следующие условия:
1) c = a b sin ,
2) c ортогонален векторам a и b ,
3) c направлен так, что тройка векторов a , b , c –
правая, то есть ориентирована одинаково с базисной
тройкой i , j , k .
[a,b]
c
Если хотя бы один из векторов
нулевой, то полагают, что
b
векторное произведение равно
нулевому вектору.
a

40.

[i , j] = k
[ j,k] = i
[i ,k] = – j
[ j, i ] = –k
[k, j] = –i
[ k , i ]= j
Свойства векторного произведения
1.
[a,b] = – [b,a]
2.
[ a , b ] = [ a , b ] = [ a , b ]
3.
[ a1 + a2 , b ] = [ a1 , b ] + [ a2 , b ]
4.
[a,a] = 0
Лемма 6.1. Векторное произведение двух ненулевых
векторов есть нулевой вектор тогда и только тогда,
когда сомножители коллинеарны.

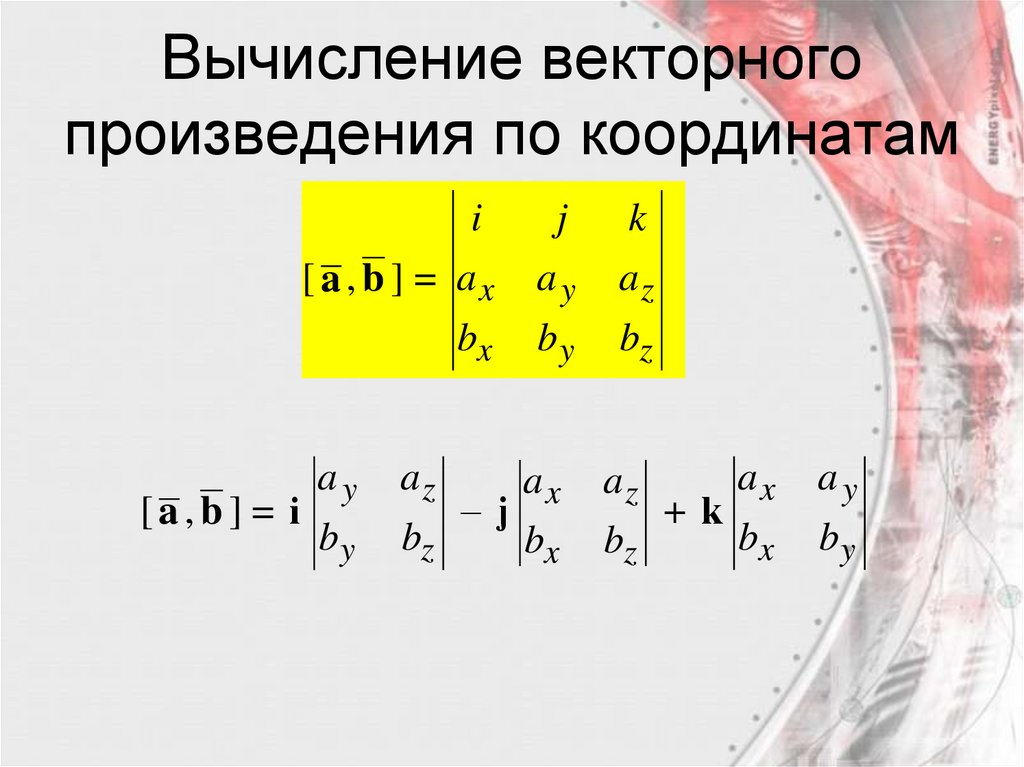
41.

Вычисление векторного
произведения по координатам
i
[ a , b ] = ax
bx
[a,b] = i
ay
az
by
bz
– j
j
k
ay
az
by
bz
ax
az
bx
bz
+k
ax
ay
bx
by

42.

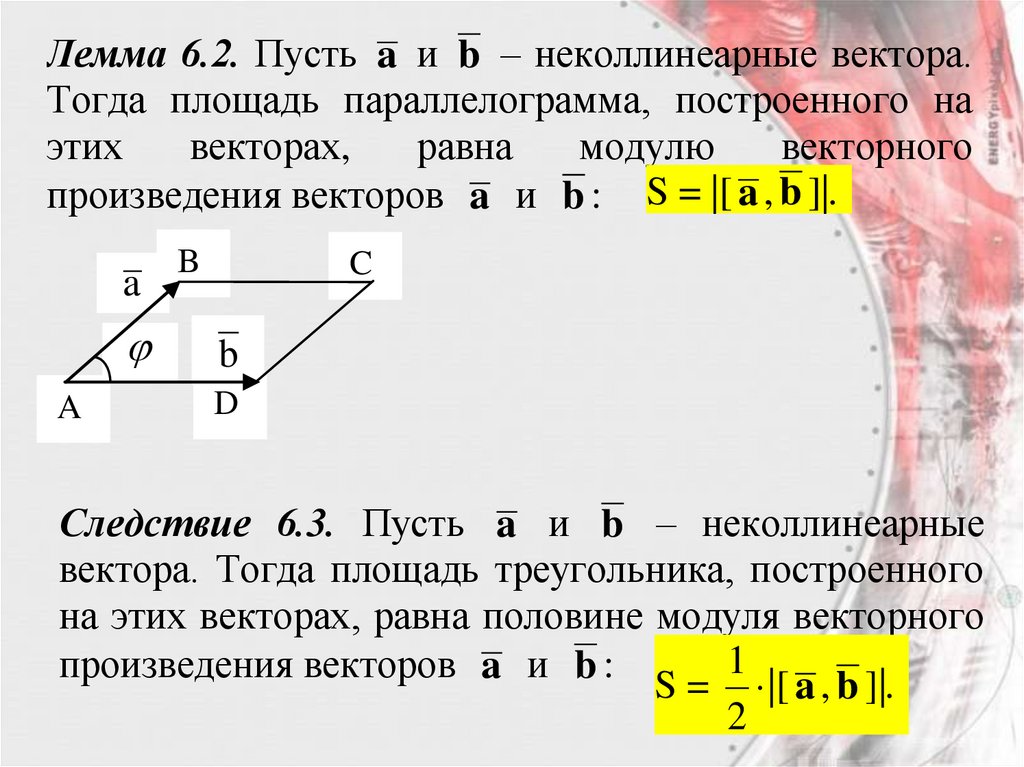
Лемма 6.2. Пусть a и b – неколлинеарные вектора.
Тогда площадь параллелограмма, построенного на
этих
векторах,
равна
модулю
векторного
произведения векторов a и b : S = |[ a , b ]|.
a
A
B
C
b
D
Следствие 6.3. Пусть a и b – неколлинеарные
вектора. Тогда площадь треугольника, построенного
на этих векторах, равна половине модуля векторного
1
произведения векторов a и b :
S = |[ a , b ]|.
2

43.

Определение. Смешанным произведением трёх
векторов a , b и c называется число, получаемое
следующим образом: векторное произведение [ a , b ]
умножаем скалярно на c :
( a , b , c ) = ([ a , b ], c ).

44.

Лемма 7.1. Пусть a , b и c – некомпланарные
вектора. Тогда объём параллелепипеда, построенного
на этих векторах, равен модулю смешанного
произведения векторов a , b и c :
V = |( a , b , c )|.
Следствие 7.2. Пусть a , b и c – некомпланарные
вектора. Тогда объём пирамиды, построенной на этих
векторах, равен одной шестой модуля смешанного
произведения векторов a , b и c :
1
V = |( a , b , c )|.
6

45.

Вычисление смешанного
произведения
Пусть a ={ a x , a y , a z }, b ={ bx , by , bz }, c ={ c x , c y , c z }.
ax
ay
az
( a , b , c ) = bx
cx
by
bz
cy
cz