Similar presentations:
Квадратные неравенства
1.
Стадия вызоваx2-5x+4=0
y=x2+3
x2-6x+5>0
y=-x2+3x-4
x2-4
x2-4x+4=0
16-x2
2.
МатематикаКвадратные неравенства
Федорова Е.А.
Учитель математики
и информатики
I категории
3.
Цель урока: сформировать у учащихсязнания о решении квадратных
неравенств средствами ТРКМ
Задачи урока:
1. Рассмотреть на примерах решение
неравенств второй степени с одной
переменной
2. Развитие математических навыков
решения квадратных неравенств
3. Воспитание познавательного
интереса к математике
4.
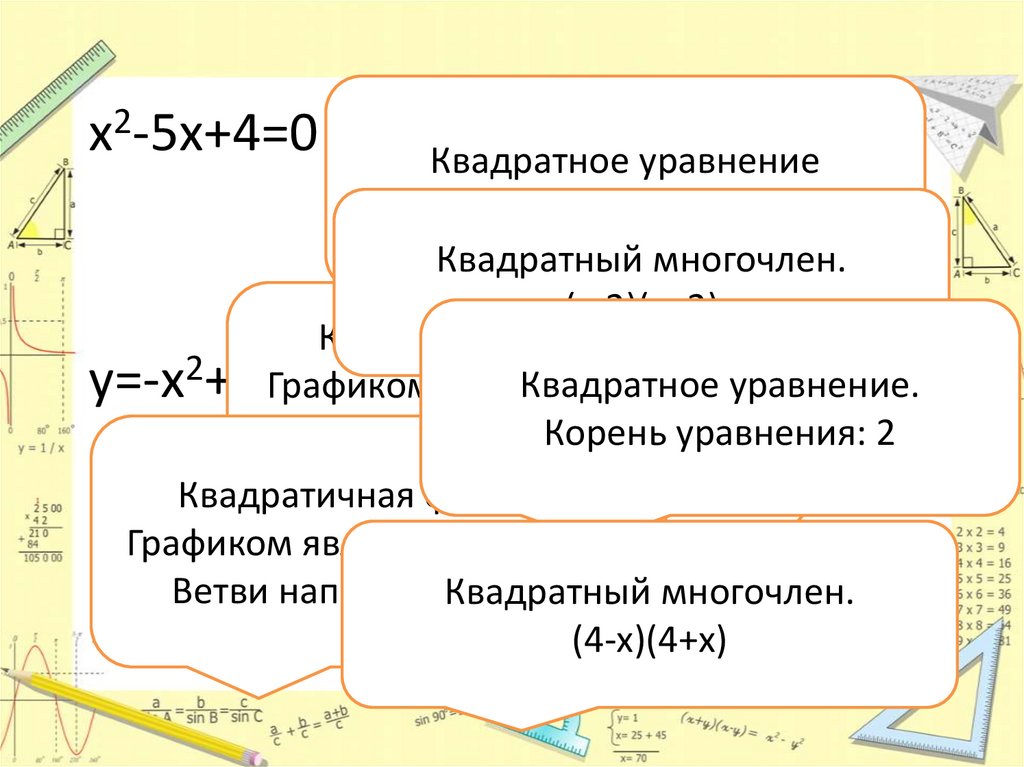
x2-5x+4=0Квадратное уравнение
Корни
уравнения: 1 и 4
y=x2+3
Квадратный многочлен.
2-6x+5>0
x
(х-2)(х+2)
Квадратичная функция.
y=-x2+3x-4
Квадратное
уравнение.
Графиком является
парабола.
Корень
уравнения: 2
Ветви направлены
вверх.
2
x
-4
(0;3)
–
точка
минимума
Квадратичная функция.
Графиком является парабола.
x2-4x+4=0
Ветви направлены
вниз.
Квадратный
многочлен.
16-x2
(4-х)(4+х)
5.
Стадия осмысления содержанияРассмотрим наше
неравенство
2
x -6x+5>0
6.
1. Графический способ1. Строим схематически у= x2-6x+5
• Отметим нули функции
• Учитывая направление ветвей
параболы, построим график
функции
2. Отмечаем промежутки,
удовлетворяющие неравенству
3. Записываем ответ.
7.
1. Графический способРешим второе
неравенство
2
-x +2x+3>0
8.
1. Графический способ1. Строим схематически у= -x2+2x+3
• Отметим нули функции
• Учитывая направление ветвей
параболы, построим график
функции
2. Отмечаем промежутки,
удовлетворяющие неравенству
3. Записываем ответ.
9.
Стадия осмысления содержанияРассмотрим наше
неравенство
2
x -6x+5>0
10.
2. Системами1. Разложим квадратный трехчлен x2-6x+5
на множители.
2. Используя свойства чисел, составить 2
системы.
3. Решить 2 системы линейных уравнений.
4. Объединить решения 2-х систем,
записав ответ.
11.
РефлексияНаписать синквейн по теме урока.
Правило составления синквейна:
1 существительное
2 прилагательных или причастия
3 глагола
Фраза (из 4 слов)
Синоним существительного
12.
РефлексияНеравенства
Линейные, квадратные
Смотрим, выбираем, решаем…
Найдем все его решения
Ответ
13.
Подведение итогов:• Сегодня на уроке мы рассмотрели 2
способа решения квадратных
неравенств: графический и системами.
• Все рассмотренные примеры содержали
случай, когда D>0.
• На следующем уроке мы рассмотрим
случаи: D<0 и D=0.
• Также далее нами будет рассмотрен 3
способ решения квадратных неравенств
– метод интервалов.
14.
Домашнее заданиеДома: §40, 41 читать,
№ 652(2,4), 660(2,4)
15.
МатематикаСпасибо за урок












 mathematics
mathematics








