Similar presentations:
Многогранники и их основные свойства
1.
Многогранники иих основные
свойства
2.
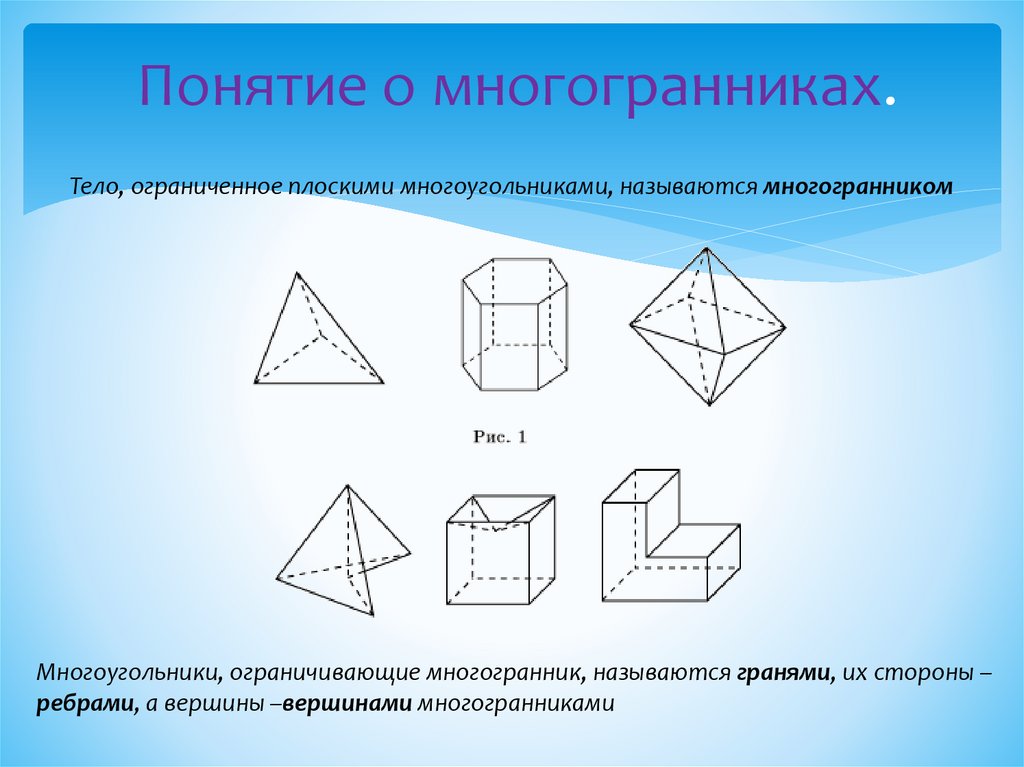
Понятие о многогранниках.Тело, ограниченное плоскими многоугольниками, называются многогранником
Многоугольники, ограничивающие многогранник, называются гранями, их стороны –
ребрами, а вершины –вершинами многогранниками
3.
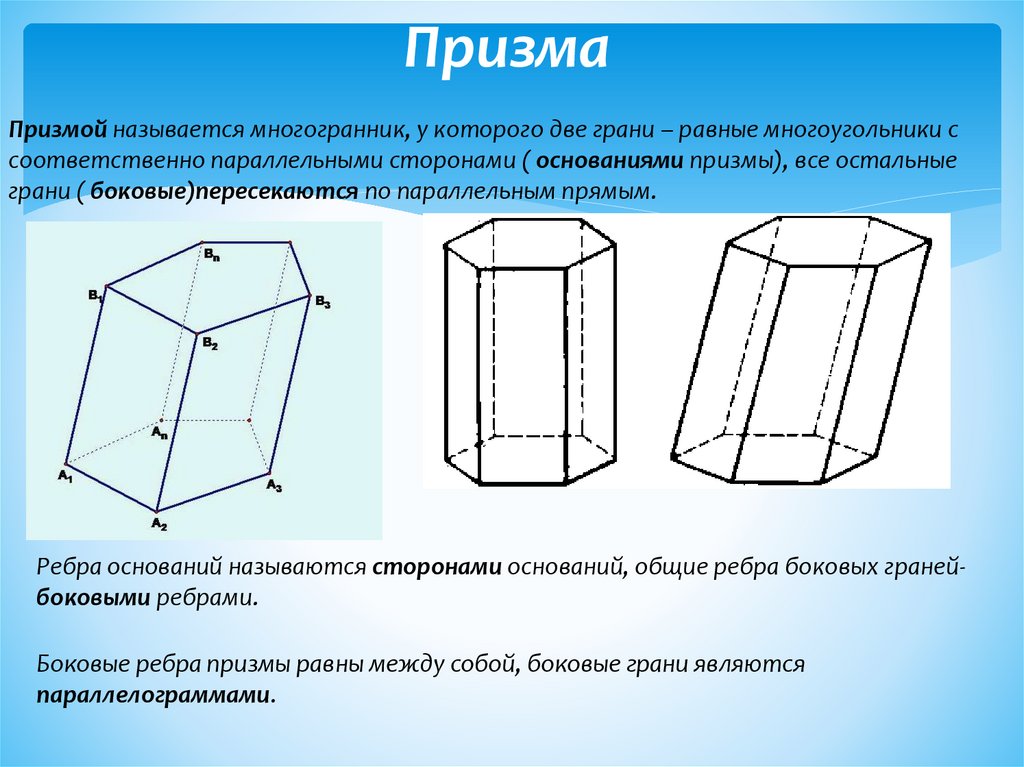
ПризмаПризмой называется многогранник, у которого две грани – равные многоугольники с
соответственно параллельными сторонами ( основаниями призмы), все остальные
грани ( боковые)пересекаются по параллельным прямым.
Ребра оснований называются сторонами оснований, общие ребра боковых гранейбоковыми ребрами.
Боковые ребра призмы равны между собой, боковые грани являются
параллелограммами.
4.
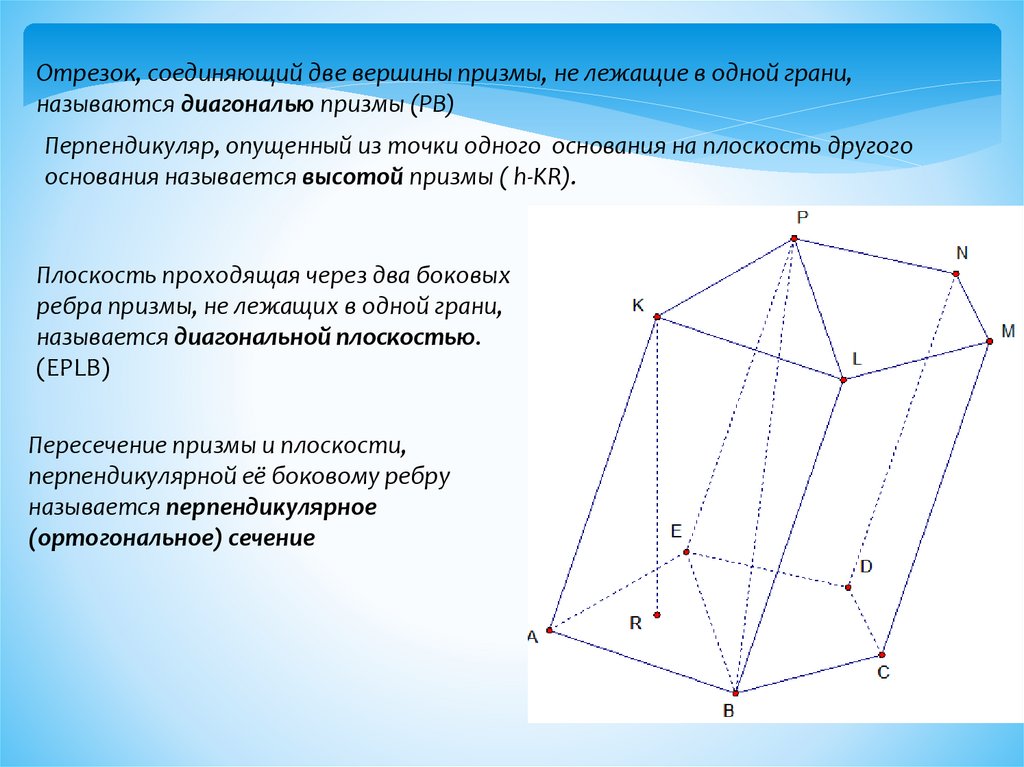
Отрезок, соединяющий две вершины призмы, не лежащие в одной грани,называются диагональю призмы (PB)
Перпендикуляр, опущенный из точки одного основания на плоскость другого
основания называется высотой призмы ( h-KR).
Плоскость проходящая через два боковых
ребра призмы, не лежащих в одной грани,
называется диагональной плоскостью.
(EPLB)
Пересечение призмы и плоскости,
перпендикулярной её боковому ребру
называется перпендикулярное
(ортогональное) сечение
5.
Свойства призмы1. Боковые ребра призмы параллельны и равны.
2. Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам
призмы.
3. Углы перпендикулярного сечения — это линейные углы двугранных углов при
соответствующих боковых рёбрах.
4. Перпендикулярное сечение перпендикулярно ко всем боковым граням
6.
ПризмаПрямая
Призму называют прямой, если плоскости
боковых граней перпендикулярны к плоскостям
оснований
Боковые грани прямой призмы - прямоугольник
Наклонная
Непрямая призма называется
наклонной
7.
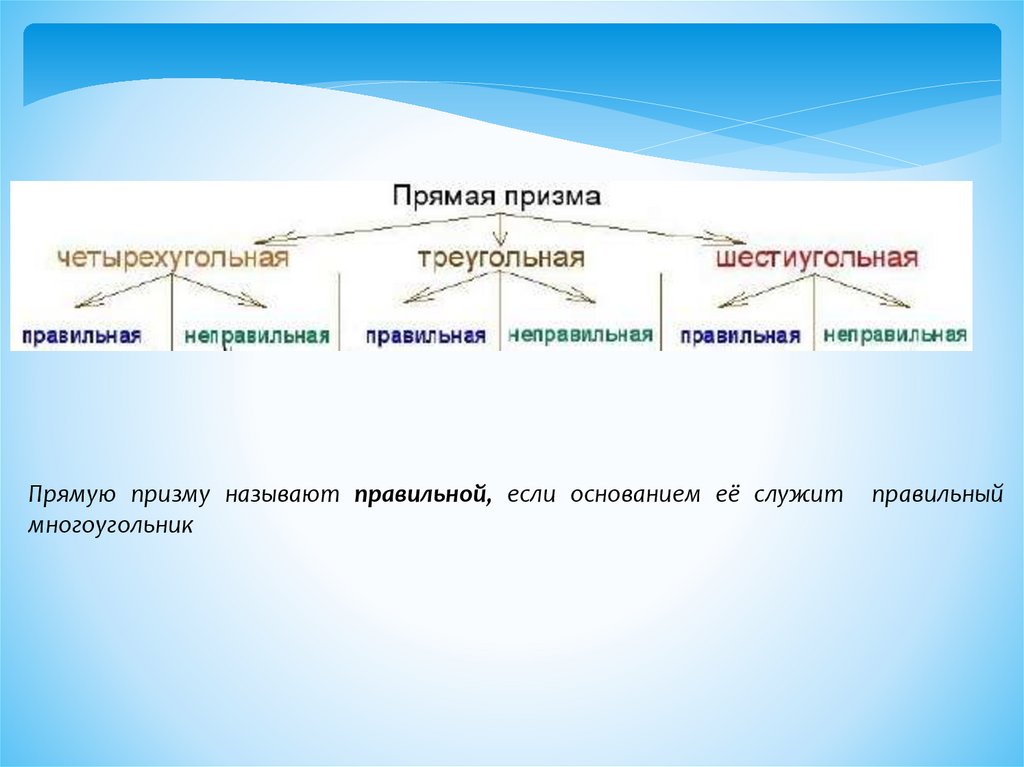
Прямую призму называют правильной, если основанием её служитмногоугольник
правильный
8.
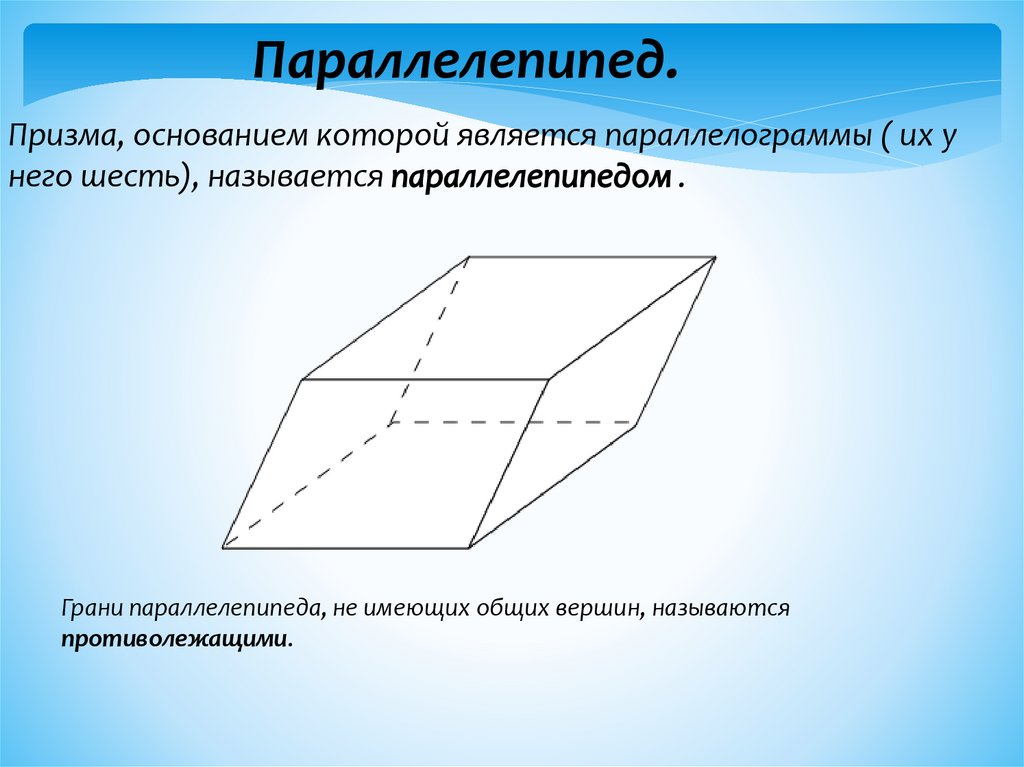
Параллелепипед.Призма, основанием которой является параллелограммы ( их у
него шесть), называется
Грани параллелепипеда, не имеющих общих вершин, называются
противолежащими.
9.
Типы параллелепипедаПрямоугольный параллелепипед — объёмная фигура, у которой шесть граней, и
каждая из них является прямоугольником.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов
трех его измерений
d a b c
2
2
2
2
10.
КубПрямоугольный параллелепипед с равными измерениями называется кубом. Все
шесть граней куба — равные квадраты
Квадрат диагонали куба равен утроенному произведению квадратов его ребер
d 3a
2
2
11.
Площади призмыSбок Pосн l
где Росн- периметр основания,
l-ребро призмы
Sполн 2Sосн Sбок
12.
Правильнаяпризма
Площадь боковой
поверхности
Площадь
основания
Треугольная
призма
3ah
a2 3
4
2S осн S бок а(
Четырехугольная
призма
4ah
а
2Sосн Sбок 2а(а 2h)
Шестиугольная
призма
6ah
3a 2 3
2
2
Площадь полной
поверхности
а 3
3h)
2
2Sосн Sбок 3а(а 3 2h)
13.
Решение задач по теме:«Призма и его виды»
14.
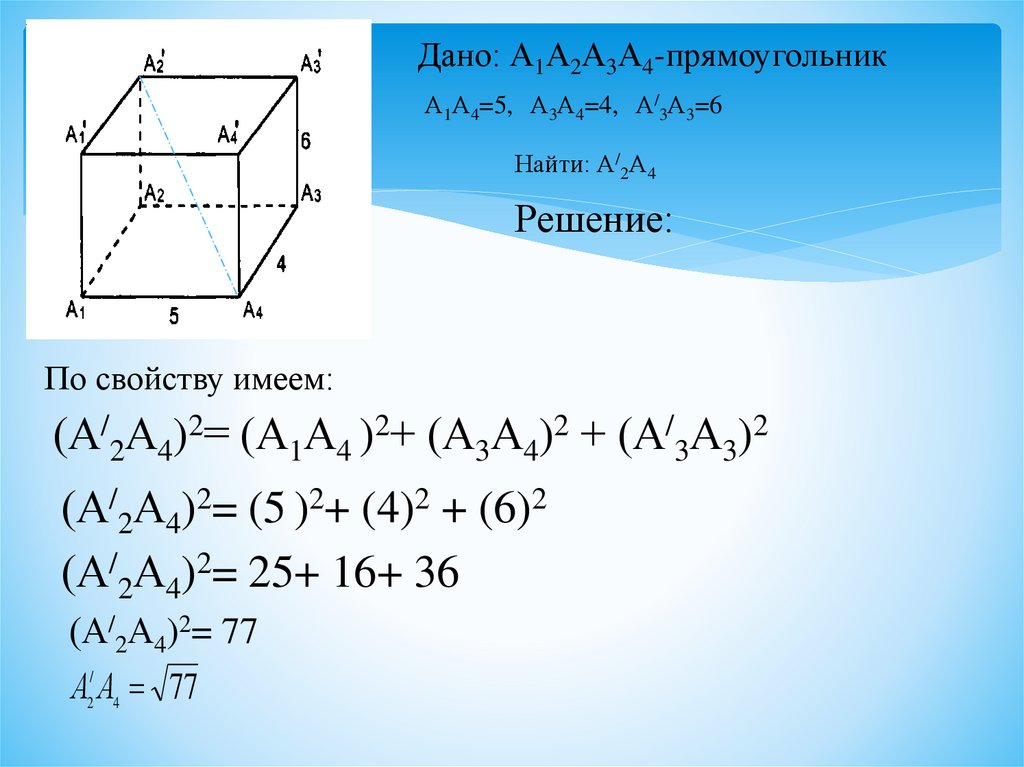
Дано: А1А2А3А4-прямоугольникА1А4=5, А3А4=4, А/3А3=6
Найти: А/2А4
Решение:
По свойству имеем:
(А/2А4)2= (А1А4 )2+ (А3А4)2 + (А/3А3)2
(А/2А4)2= (5 )2+ (4)2 + (6)2
(А/2А4)2= 25+ 16+ 36
(А/2А4)2= 77
А2/ А4 77
15.
1.Найдите
диагональ
прямоугольного
параллелепипеда, если его измерения равны:
1,1,2
2. Найдите диагональ прямоугольного
параллелепипеда, если его измерения равны:
8,9,12
3. Найдите диагональ прямоугольного
параллелепипеда, если его измерения равны:
12,16,21
16.
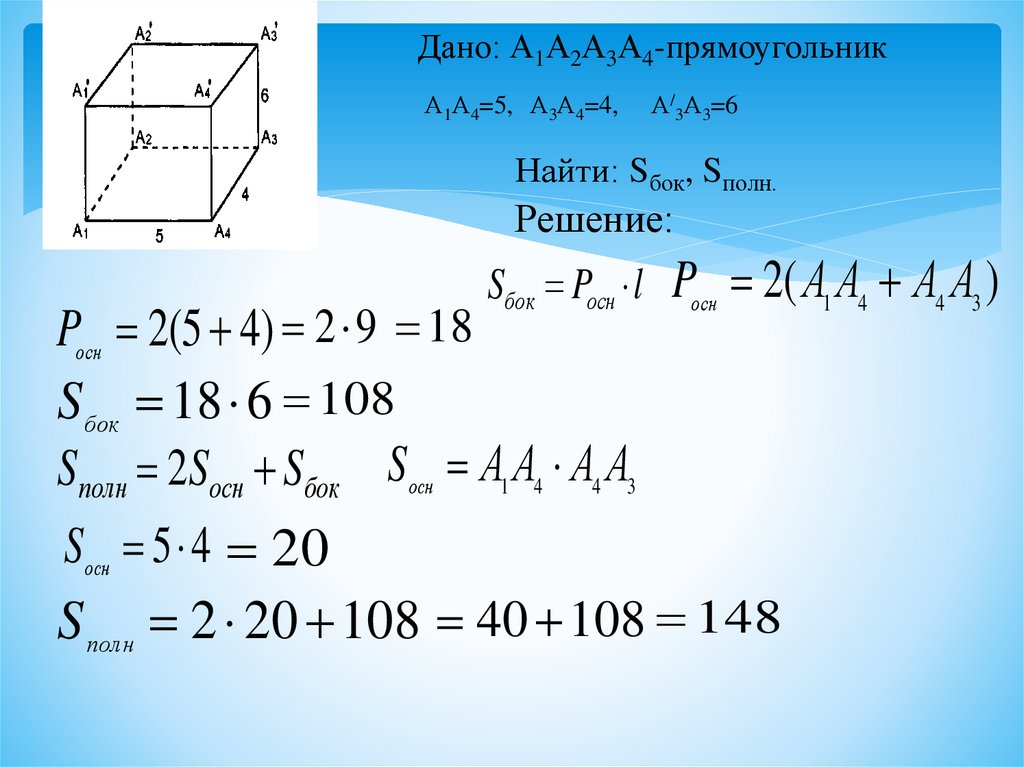
Дано: А1А2А3А4-прямоугольникА1А4=5, А3А4=4,
А/3А3=6
Найти: Sбок, Sполн.
Решение:
Sбок Pосн l
Pосн 2( А1 А4 А4 А3 )
Pосн 2(5 4) 2 9 18
S бок 18 6 108
Sполн 2Sосн Sбок Sосн А1 А4 А4 А3
Sосн 5 4 20
S полн 2 20 108 40 108 148
17.
Дано: А1А2А3 –призма, А1А2=13,А1А3=14, Sполн =378 А3А2=15,
Найти: А/1А1
Решение:
Sполн 2Sосн Sбок
2 S осн S бок 378
Sосн р( р а)( р в)( р с)
15 14 13 42 21
а в с
р
р
2
2
2
Sосн 21(21 15)(21 14)(21 13)
18.
Sосн 21 6 7 8S осн 3 7 2 2 84
Sбок Pосн l
Pосн 13 14 15 42
2 84 42 А1 А1 378
/
168 42 А1 А1 378
/
42 А1 А1 378 168
/
42 А1 А1 210
/
А1 А1 210 : 42
/
А1 А1 5
/
19.
4.Найдите площади полной и боковойповерхности призмы , если дана
правильная
треугольная
призма,
с
основанием 10 и боковым ребром 15.
(50 3 450)
5.Найдите площади полной и боковой
поверхности призмы , если дана
правильная четырехугольная призма, с
основанием 12 и высотой 8












 mathematics
mathematics








