Система линейных уравнений

1.

2.

Система m линейных уравнений с n
переменными в общем случае имеет вид:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
...
am1 x1 am 2 x2 ... amn xn bm
1

3.

Где числа
aij
(i 1,2...m,
j 1,2...n)
называются
коэффициентами
переменных;
bi - свободные члены;
xj
- переменные.
Иначе систему (1) можно записать:
n
a x
j 1
ij
j
bi
i 1,2...m
при

4.

Решением системы линейных уравнений
называется такая совокупность чисел
k1, k2,…kn
при подстановке которых каждое
уравнение обращается в верное
равенство.

5.

Система называется совместной, если
она имеет хотя бы одно решение.
Система называется определенной, если
она имеет ровно одно решение.
Система называется неопределенной, если
она имеет более одного решения.
Система называется несовместной, если
она не имеет решений.

6.

Запишем систему уравнений в матричной
форме.
Обозначим:
a11
a21
A
...
a
m1
a12
a22
am 2
... a1n
... a2 n
... amn
– матрица коэффициентов при переменных
или матрица системы

7.

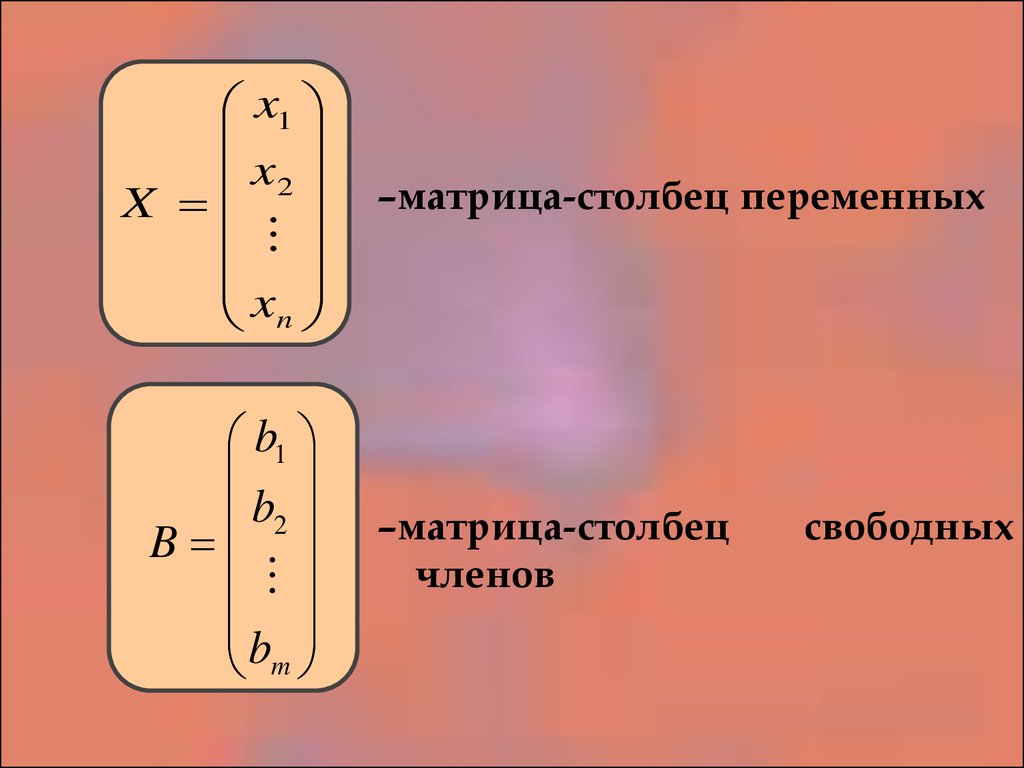
x1
x2
X
x
n
b1
b2
B
b
m
–матрица-столбец переменных
–матрица-столбец
членов
свободных

8.

Рассмотрим произведение:
a11 x1 a12 x2 ... a1n xn
a21 x1 a22 x2 ... a2 n xn
A X
...
a x a x ... a x
m2 2
mn n
m1 1
-
матрица-столбец, элементами которой
являются левые части системы (1).
Тогда в матричной форме систему (1) можно
записать:
АХ=В