Similar presentations:
Формула Ньютона-Лейбница. Площадь криволинейной трапеции
1.
Тема:Формула
Ньютона-Лейбница.
Площадь криволинейной
трапеции .
2.
3.
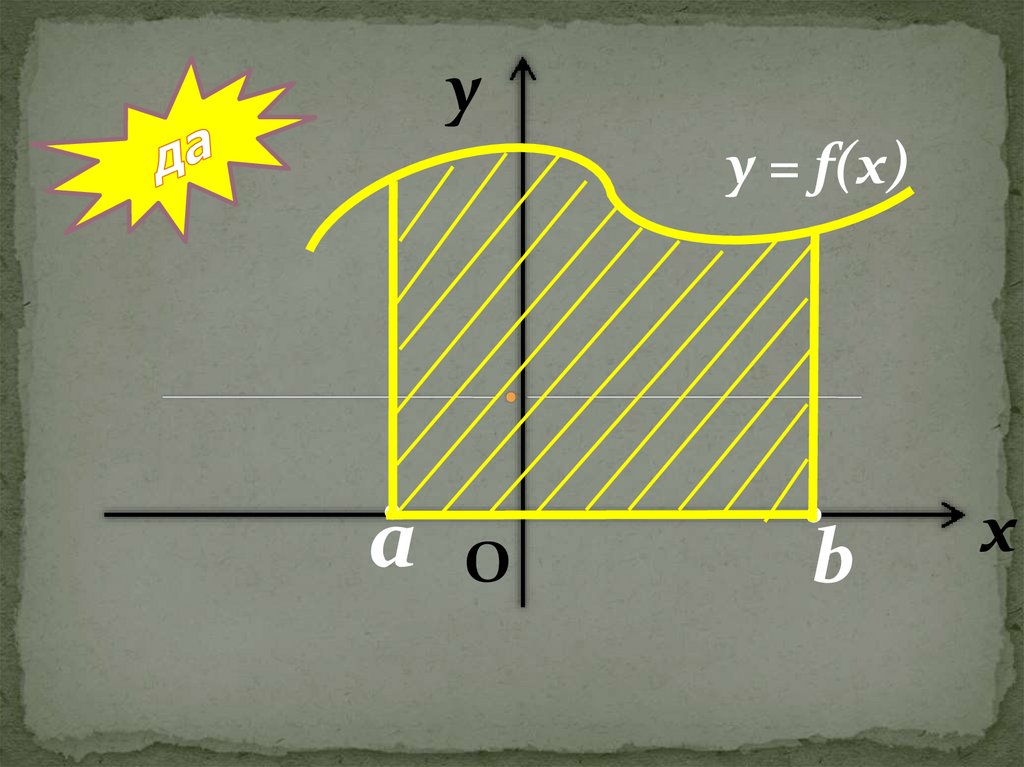
уy = f(x)
a
О
b
х
4.
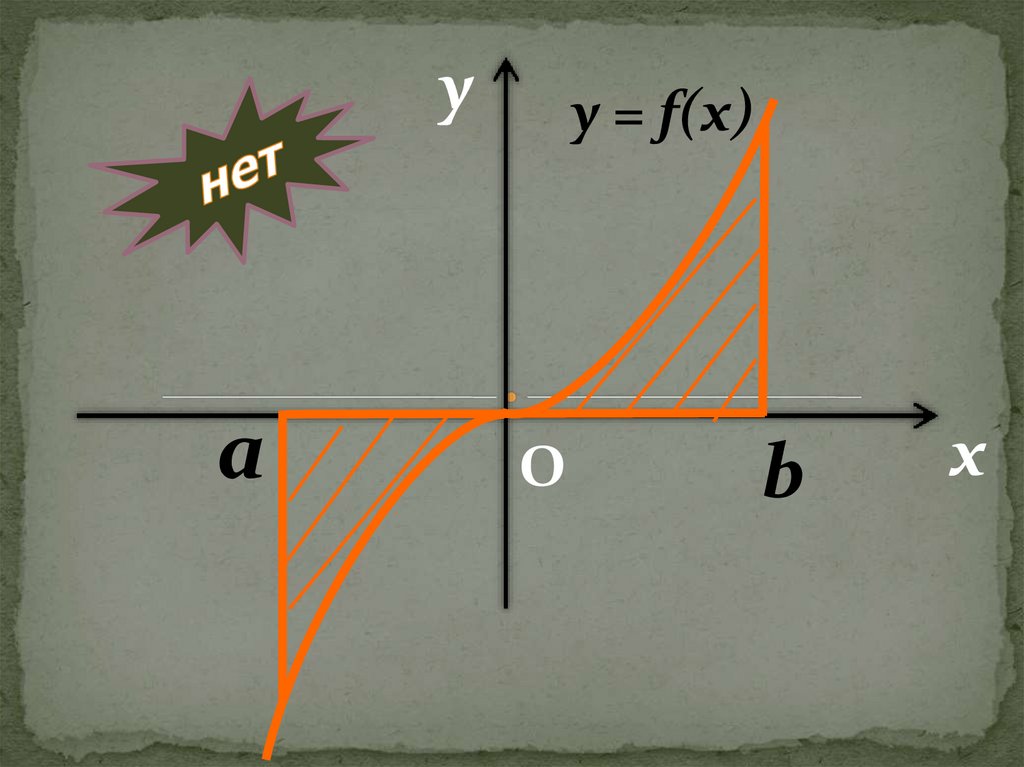
уa
y = f(x)
О
b
х
5.
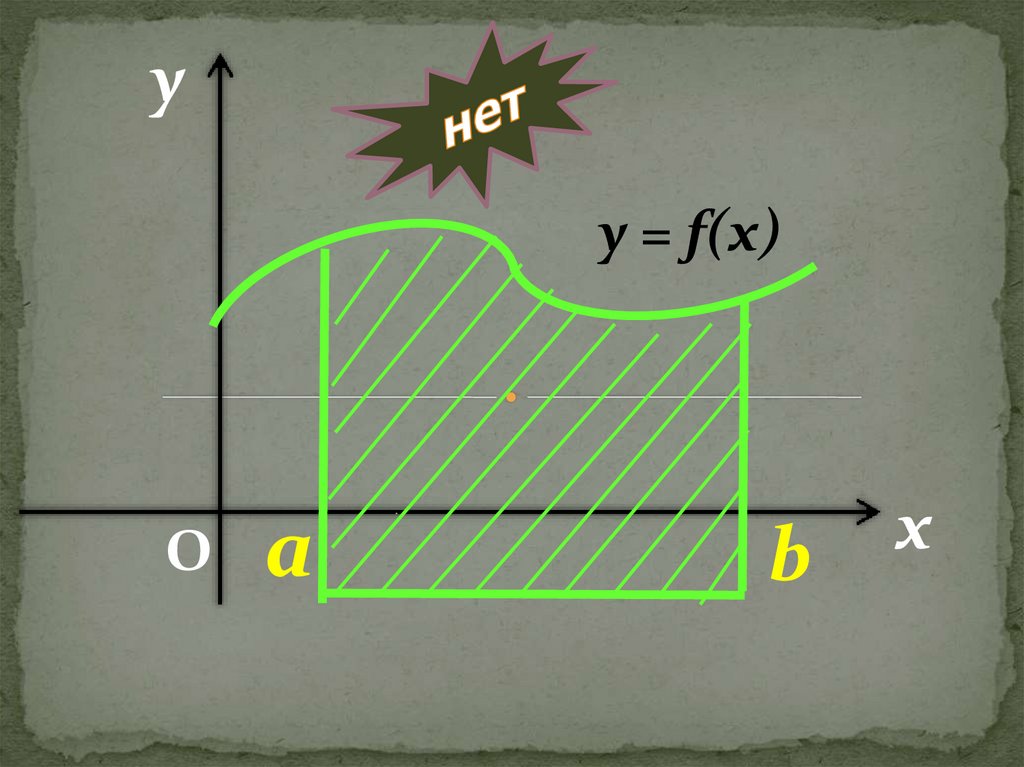
уО
y = f(x)
a
b
х
6.
уy = f(x)
О
a
b
х
7.
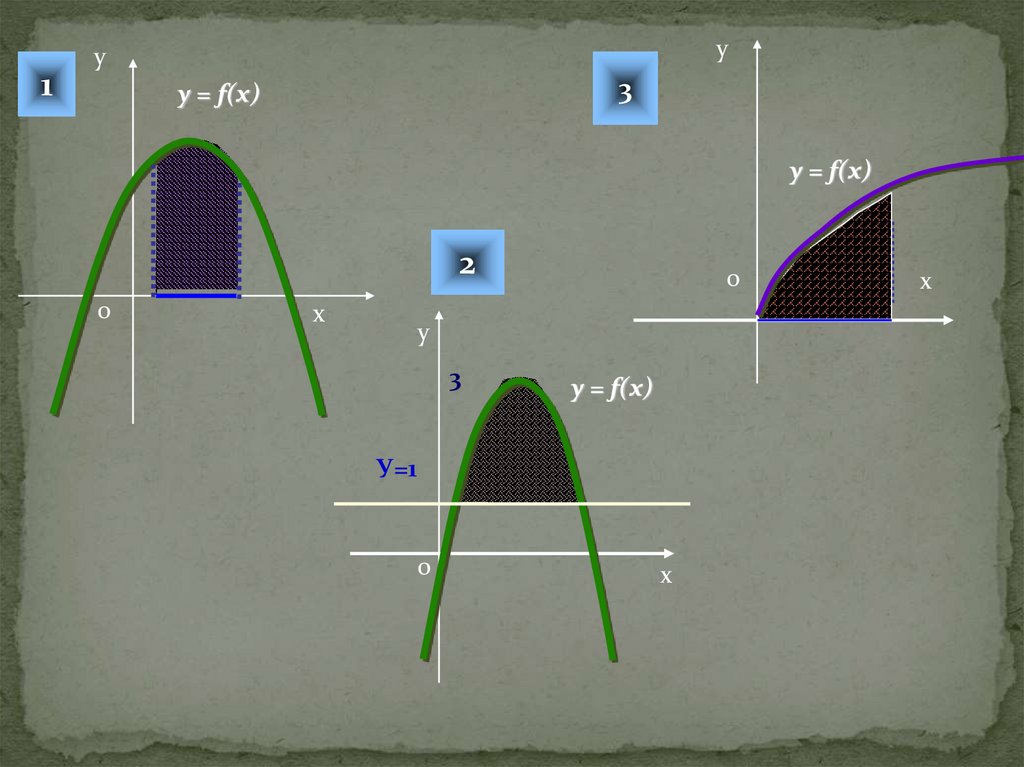
1у
у
3
y = f(x)
y = f(x)
2
0
х
0
у
3
y = f(x)
У=1
0
х
х
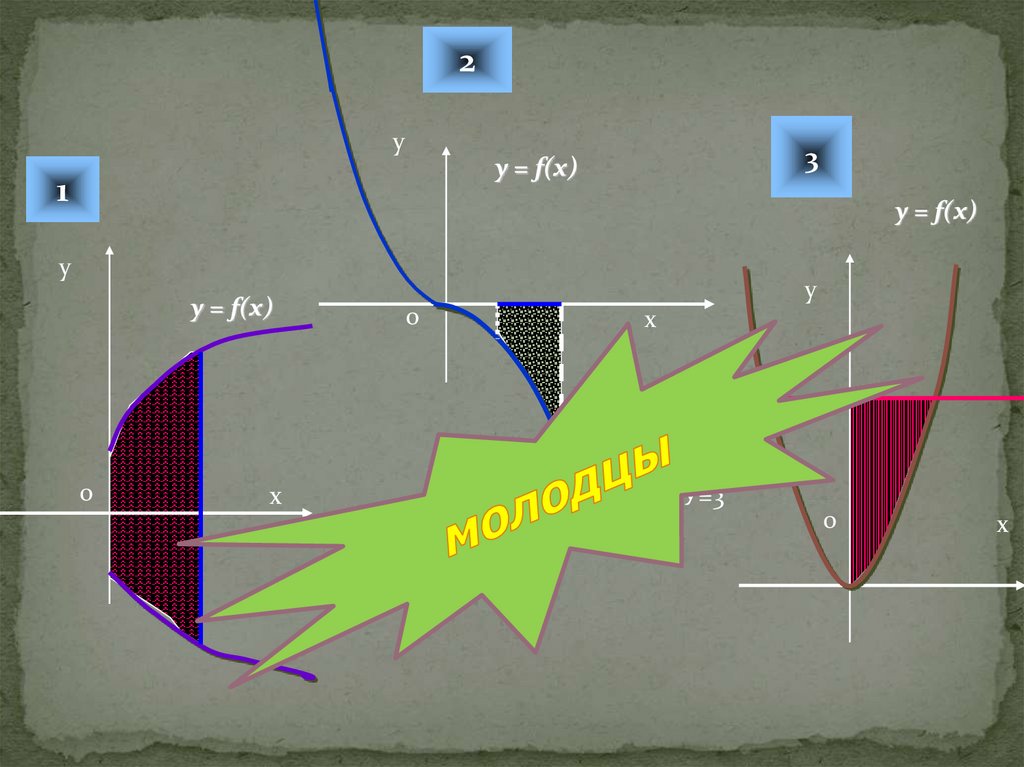
8.
2у
3
y = f(x)
1
y = f(x)
у
y = f(x)
0
х
у
0
х
У=3
0
х
9.
10.
Теоретический тест1.Если для любого х из множества Х
выполняется равенство F / ( x) f ( x)
то функцию F(x) называют …
для функции f(x) на данном
множестве.
А) производной;
В) обратной;
С) первообразной;
D) непрерывной.
11.
2. Если F(x) есть первообразнаядля функции f(x), то для
f(kx + b) первообразная имеет
вид ….
А) k F(x);
1
В) F(kх + b);
k
С) k F(kх);
1
D) F(x).
k
12.
3. Найдите множествопервообразных для функции
f(x) = 9
А) 0;
В) 9х ;
С) х + С;
D) 9х +С.
13.
4. Криволинейной трапециейназывается фигура, ограниченная
сверху:
А) Отрезком [a;b] оси ОХ;
В) Графиком непрерывной,
неотрицательной функции y = f(x);
С) Линиями: х = а, х = b
D) Осью ОХ.
14.
5. Площадь криволинейнойтрапеции вычисляется
по формуле:
А) S = F(b) – F(a);
В) S = f(b) – f(a);
С) S = f(a) – f(b) ;
D) S = F(а) – F(b).
15.
6. С помощью формулыНьютона – Лейбница
вычисляют…
А) неопределенный интеграл;
В) производную;
С) обратную функцию;
D) определенный интеграл.
16.
№вопроса
Вариант
ответа
1
2
3
4
С В D В
5
6
А D
Правильный ответ – 1 балл.
В оценочный лист отметьте
количество баллов, полученные
за тест.
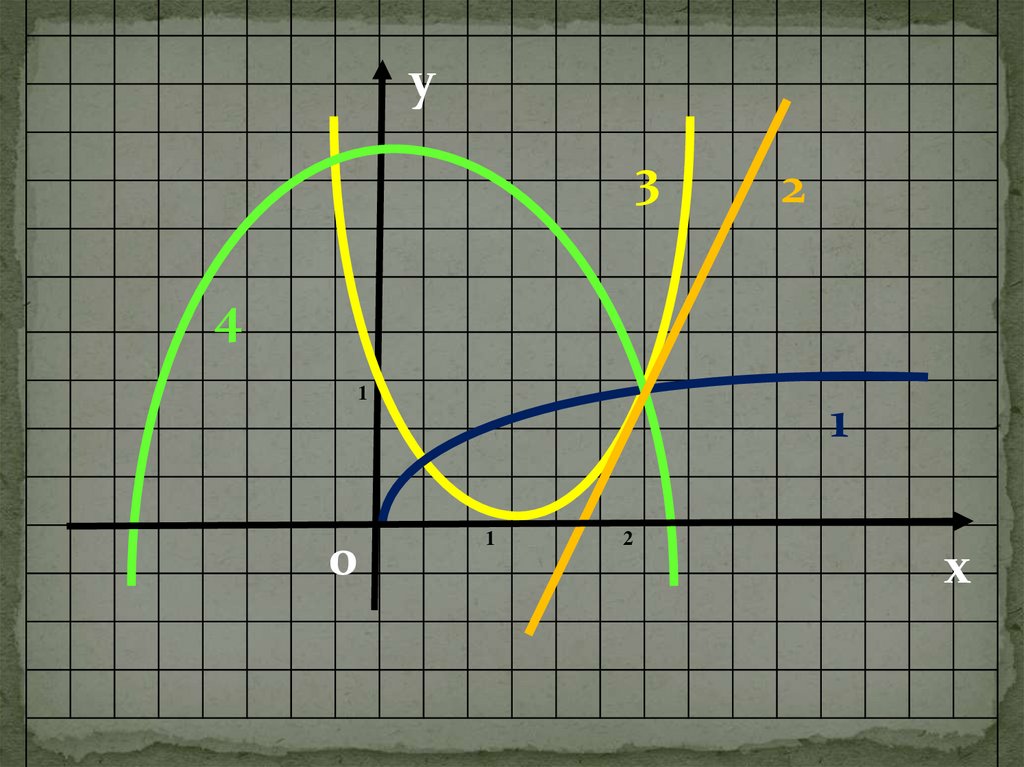
17.
«Для функции f(x) = 2х – 2найдите первообразную F(x),
график которой проходит через
точку В(2;1). Начертите график
функции F(x)».
18.
у3
2
4
1
0
1
1
2
х
19.
f(x) = 2x – 2 ,В( 2; 1)
1.Найдем все первообразные функции f(x):
1 1
x
2
F(x) = 2
2 x C х 2 x C,
1 1
2.Подставим координаты точки В: х = 2;F(x) =1
1 2 2 2 C,
2
1 4 4 C,
C 1,
3.Первообразная, график которой проходит
через точку В, имеет вид:
F ( x) х 2 x 1.
2
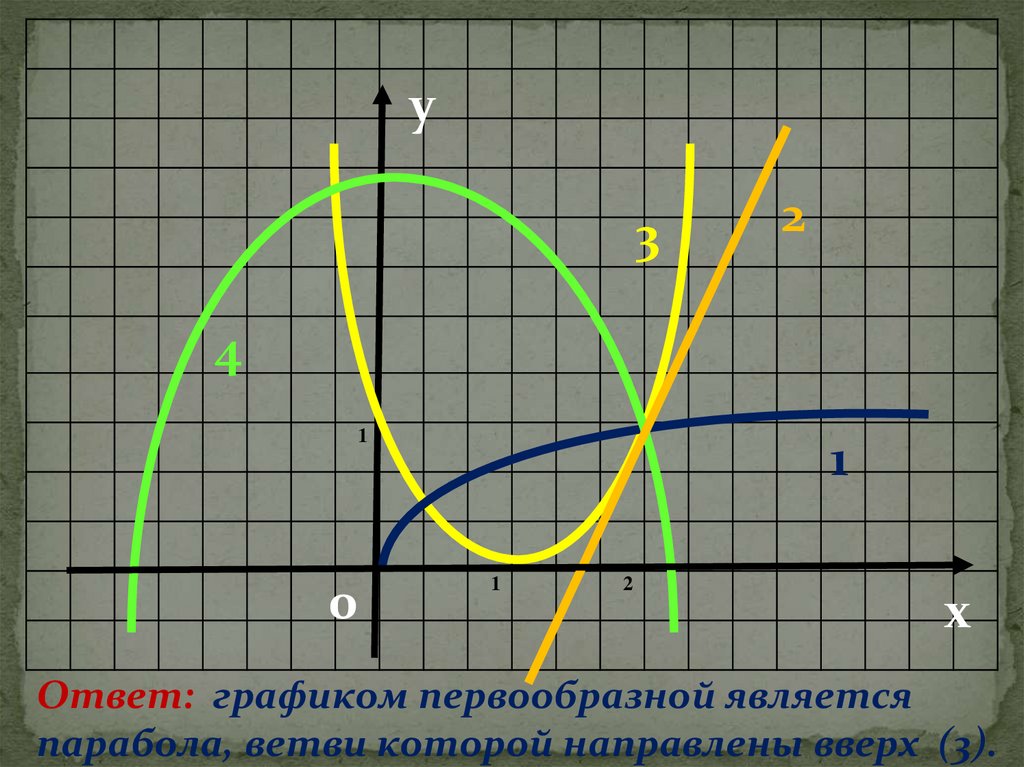
20.
у3
2
4
1
0
1
1
2
х
Ответ: графиком первообразной является
парабола, ветви которой направлены вверх (3).
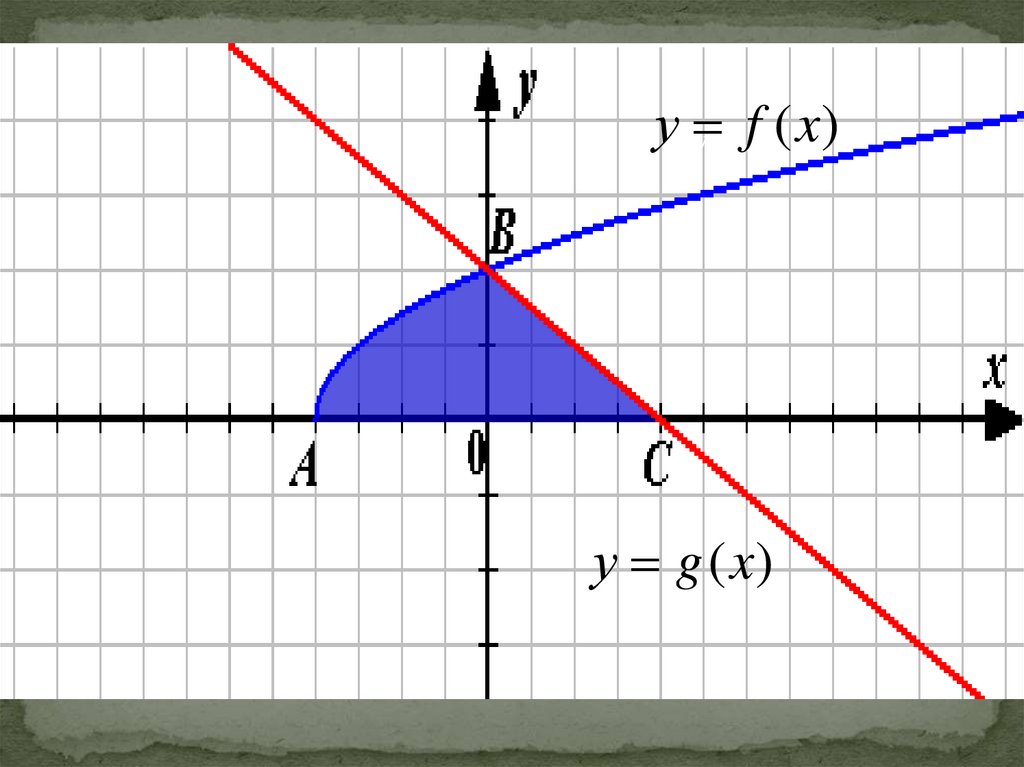
21.
y=f(x)у У=f(x)
f (x)
у g (x)
22.
23.
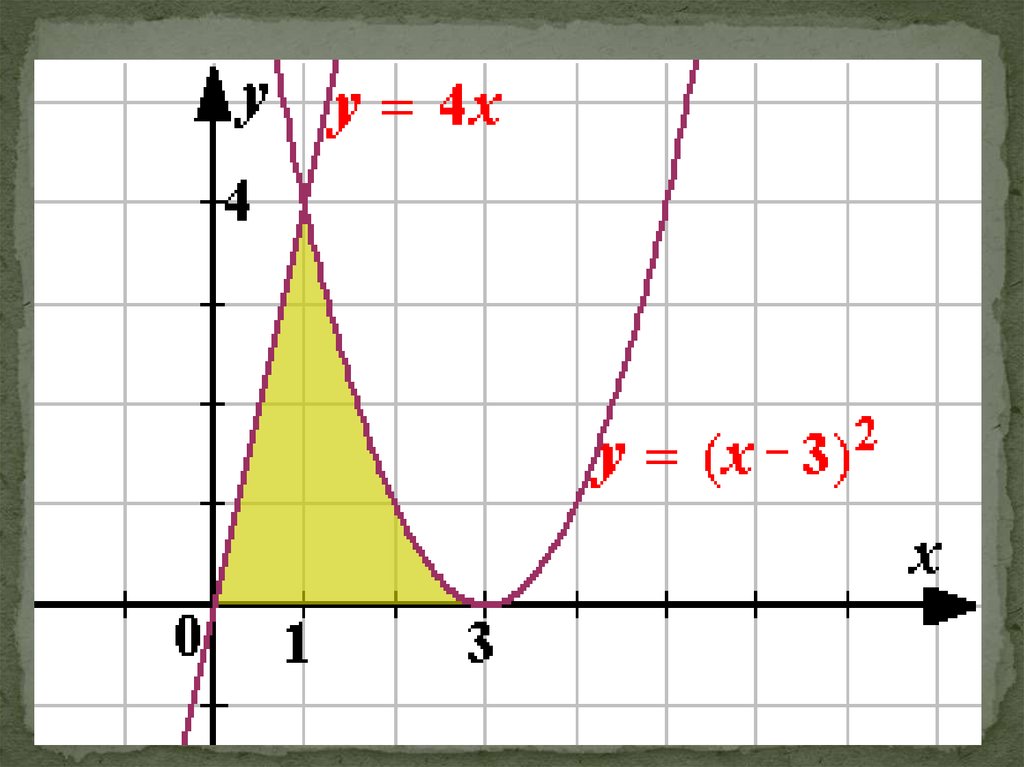
№124.
S13
x 0
dx
4
х
| 2
3
4 x
0
2
2
3
2
8
0 ( 8 )
0
4
2
3
3
8
24 8 16
1
8
5 ( кв .ед)
3
3
3
3
1
S 2 4 4 8 кв.ед
2
1
1
S 5 8 13 кв.ед
3
3
1
Ответ: S 13 кв.ед
3
25.
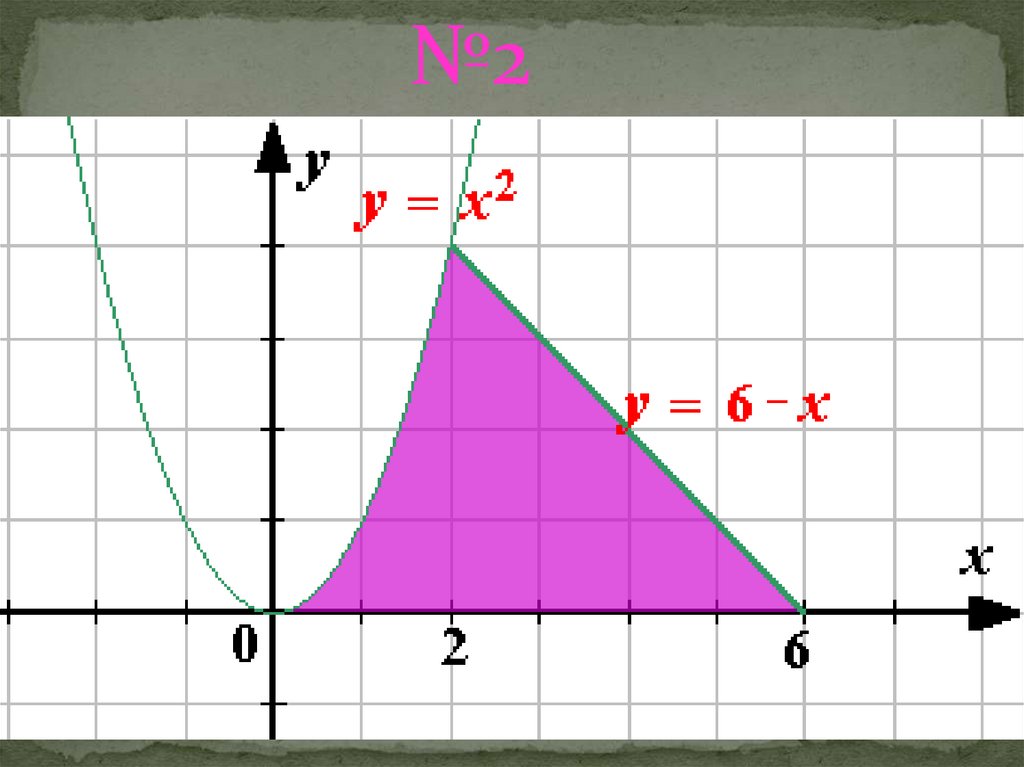
№226.
2х 2 2
8
2
S1 х dx
|0
0 2 (кв.ед)
3
3
3
3
0
3
3
2
1
S 2 4 4 8 кв.ед
2
2
2
S 2 8 10 кв.ед
3
3
Ответ:
2
S 10 кв.ед
3
27.
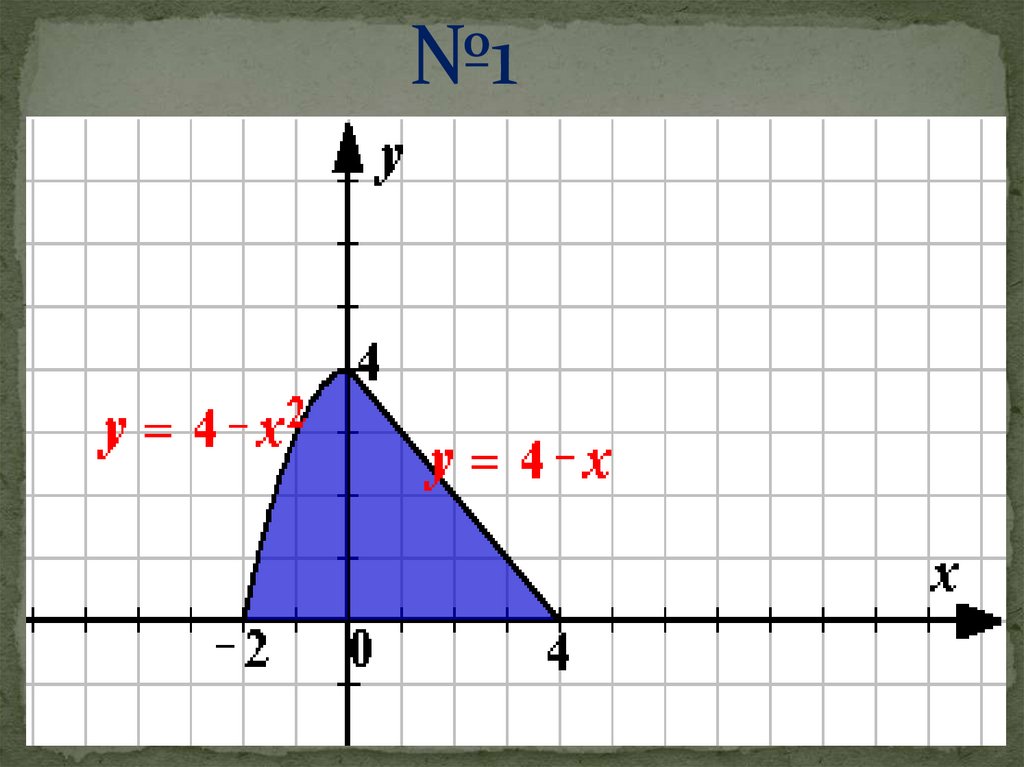
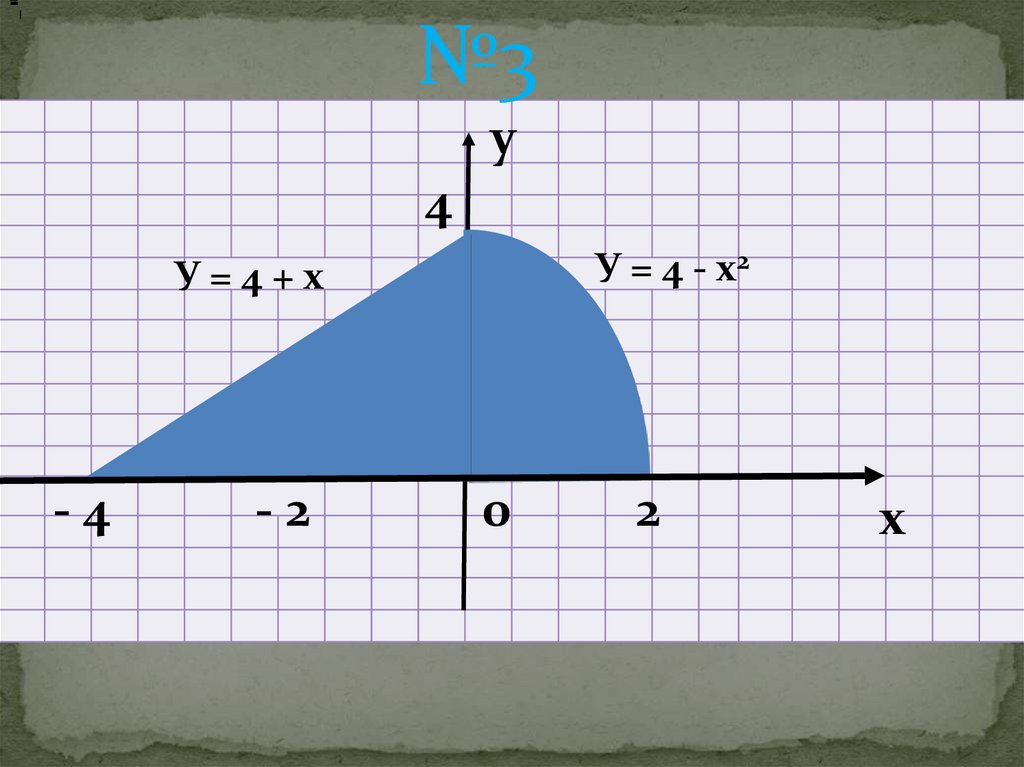
№3у
4
У = 4 - х2
У=4+х
-4
-2
0
2
х
28.
S13
x 2
dx
4х 3
|0
4 x
2
2
0
23
8
4 2 3
0 8 3
24 8
16
1
5 ( кв.ед)
3
3
3
1
1
1
S 2 4 4 8 кв.ед S 5 3 8 13 3 кв.ед
2
1
S
13
кв
.
ед
Ответ:
3
29.
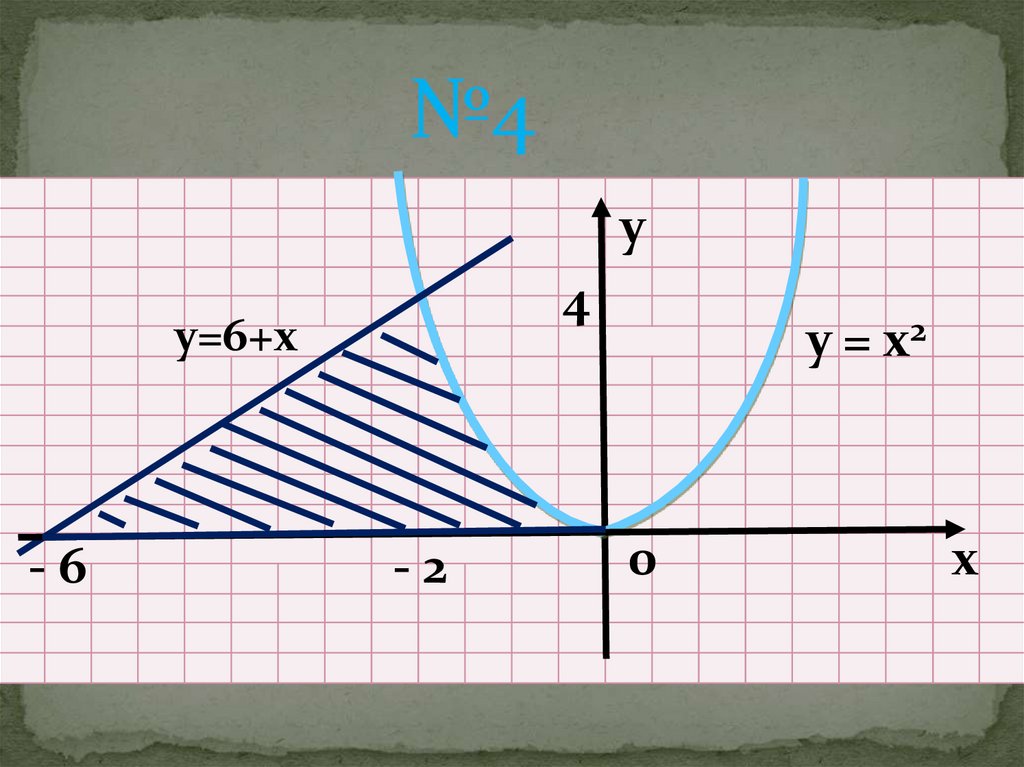
№4у
4
у=6+х
-6
-2
у = х2
0
х
30.
х 0( 2)
8
2
S1 х dx | 2 0
2 (кв.ед)
3
3
3
3
2
0
3
3
2
1
S 2 4 4 8 кв.ед
2
2
2
S 2 8 10 кв.ед
3
3
Ответ:
2
S 10 кв.ед
3
31.
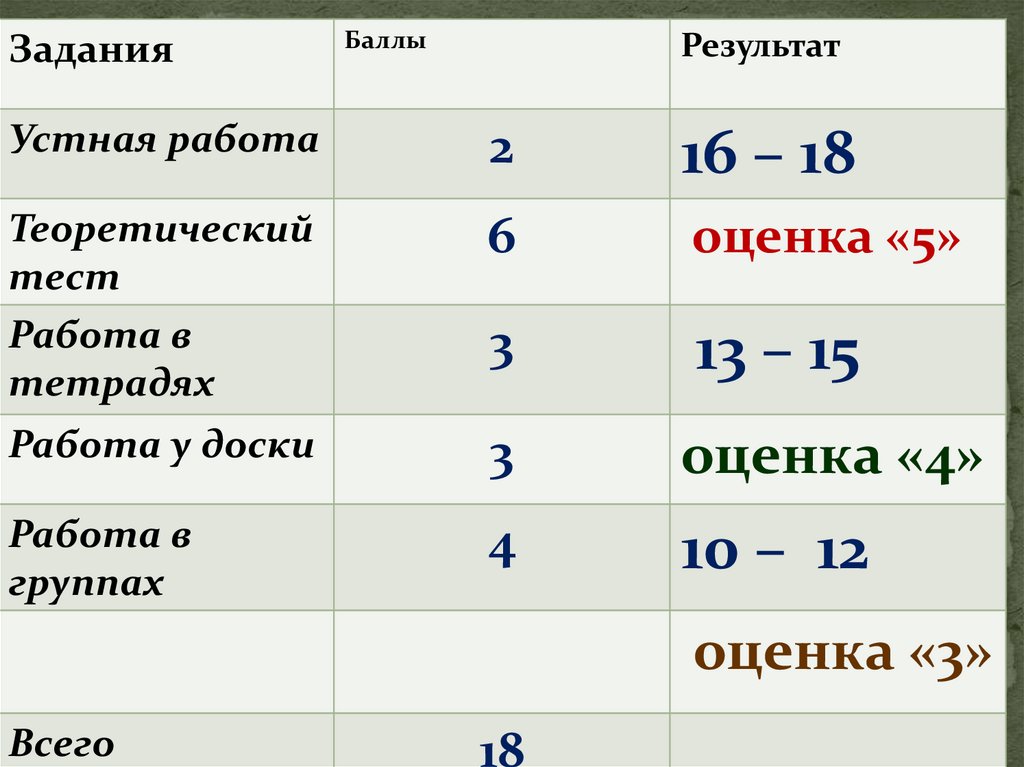
ЗаданияБаллы
Результат
Устная работа
2
16 – 18
Теоретический
тест
Работа в
тетрадях
6
оценка «5»
3
13 – 15
Работа у доски
3
оценка «4»
Работа в
группах
4
10 – 12
оценка «3»
Всего
18
32.
Эталон ответов:I вариант
II вариант
1 а) --
б) --
в) +
2 а) +
б) --
в) +
г) -г) --
а) +
б) --
а) +
б) +
у
в) -в) --
г) -г) --
у
4
2
3
-1 0 2
0 1
х
2
3
x3 2
x
S 6 x dx 6 х | 1 S 8 x 2 dx 8 х |2 1
1
3
3
1
3
3
3
23
1
2
1
8 2 8 1
6 2 6 1
3
3
3
3
28 17 45
40 23 63
15(кв.ед)
21(кв.ед)
2
4
-1
х
2
33.
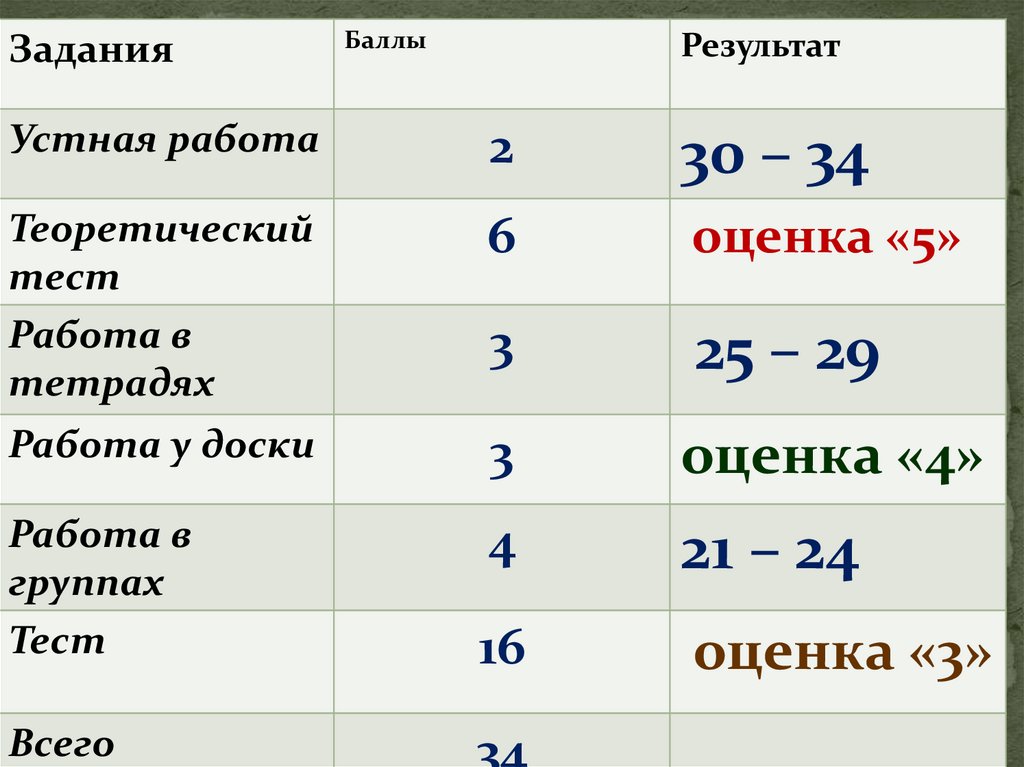
ЗаданияБаллы
Результат
Устная работа
2
30 – 34
Теоретический
тест
Работа в
тетрадях
6
оценка «5»
3
25 – 29
Работа у доски
3
оценка «4»
Работа в
группах
Тест
4
21 – 24
16
оценка «3»
Всего
34














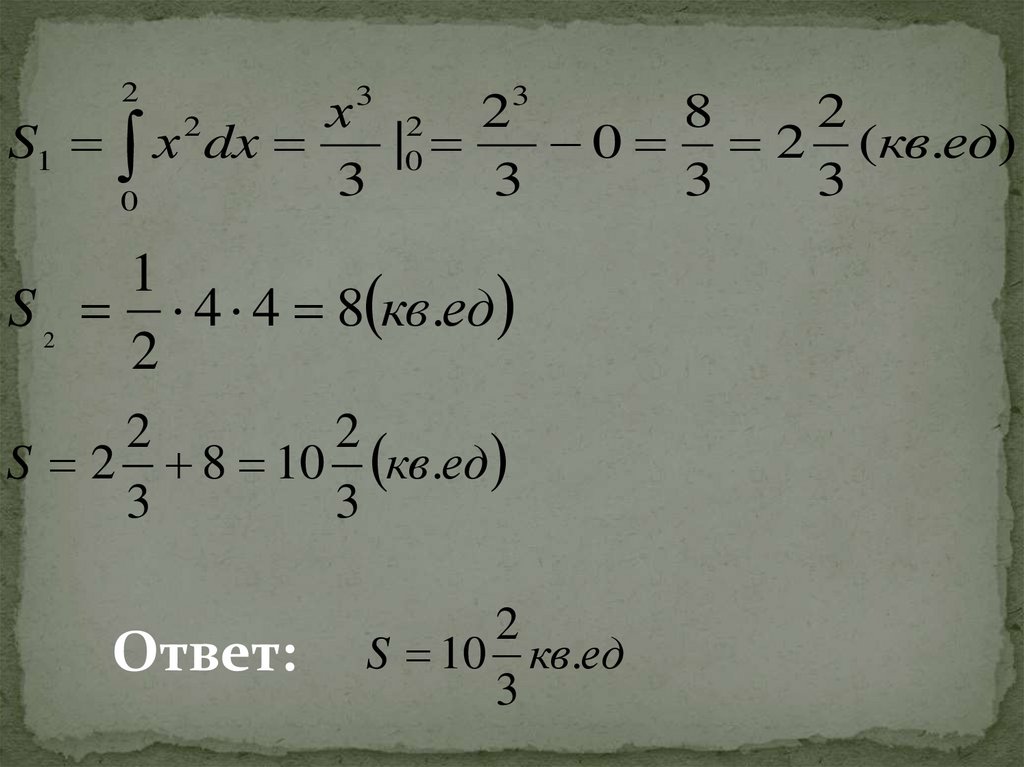
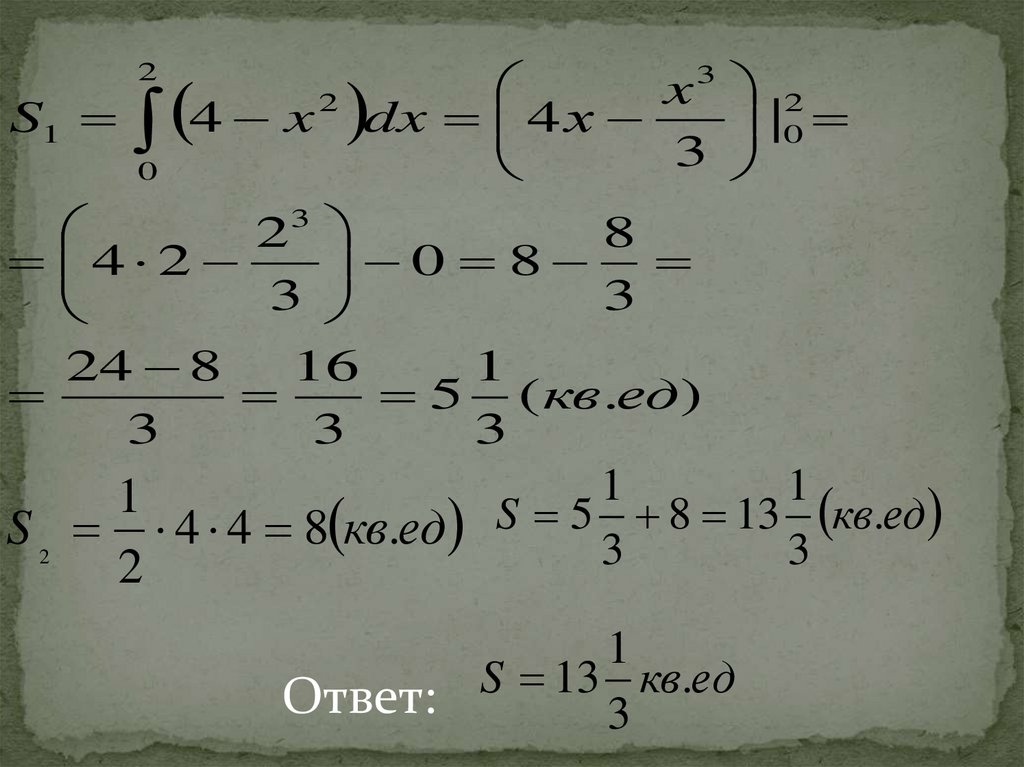
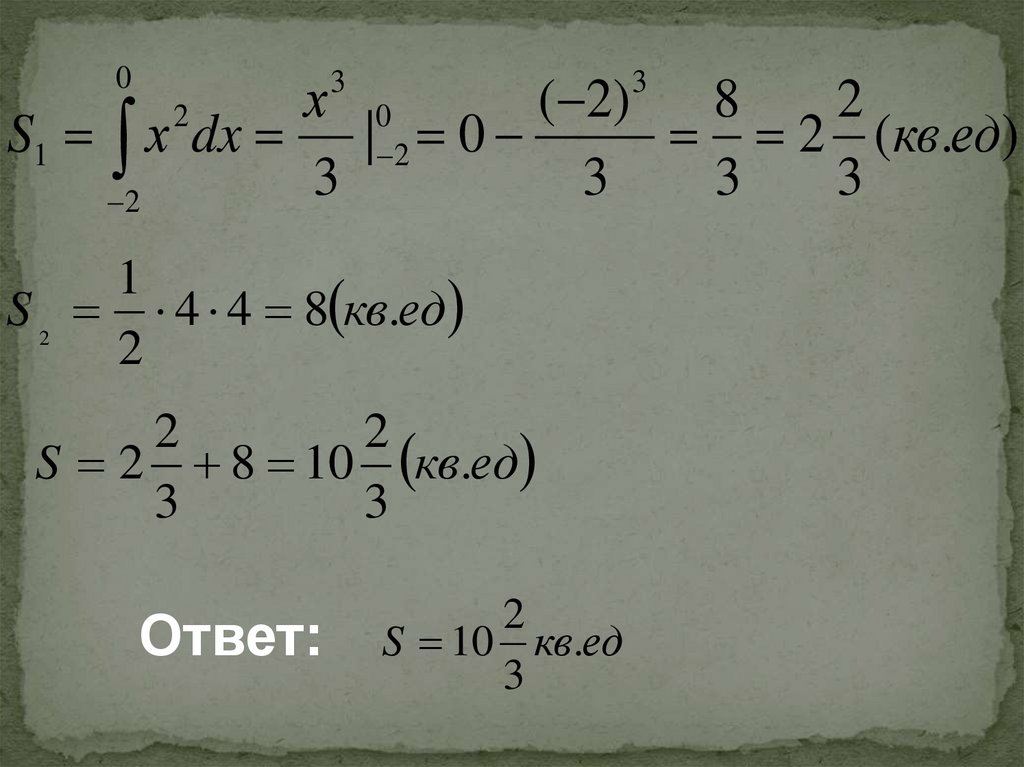

 mathematics
mathematics








