Теория нечетких множеств

1.

Теория нечетких множеств

2.

Лотфи Аскер Заде
(в научных работах обычно Лотфи
Заде или Лотфи А. Заде, азерб.
Lütfi Əsgər Zadə — Лютфи Аскер
Заде, англ. Lotfi Asker Zadeh —
Лотфи А. Заде) — американский
математик,
основатель
теории
нечётких множеств и нечёткой
логики,
профессор
Калифорнийского
университета
(Беркли).
2

3.

3

4.

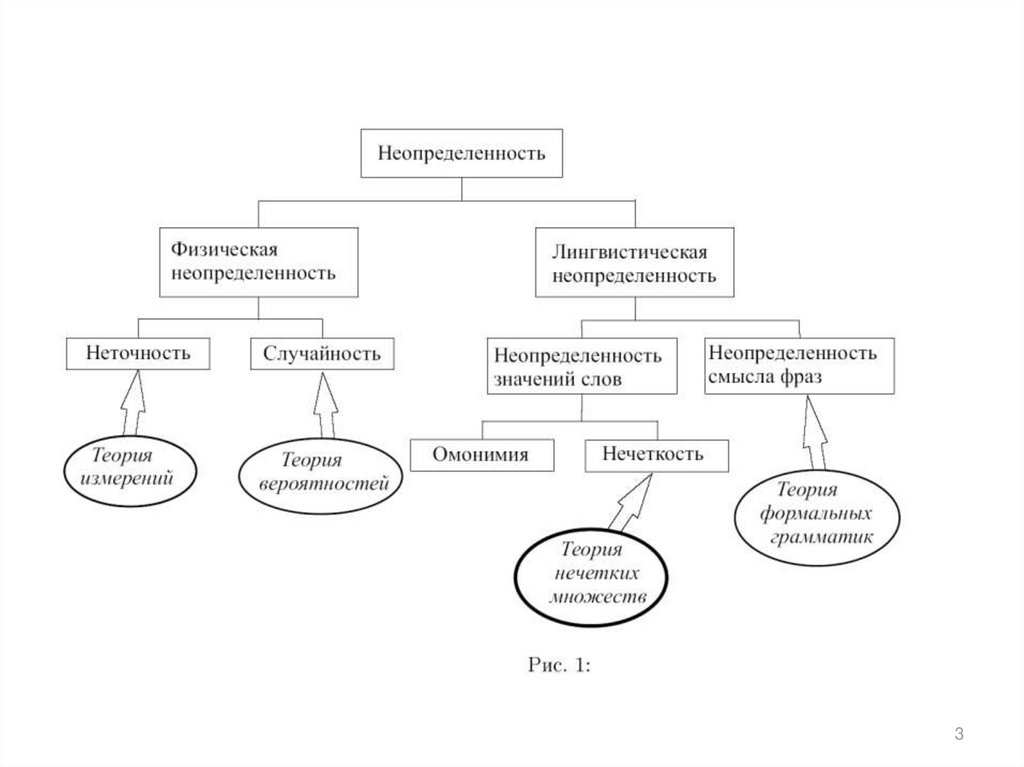
Неопределенность
Нечеткость
НЕДЕТЕРМИНИРОВАННОСТЬ
4

5.

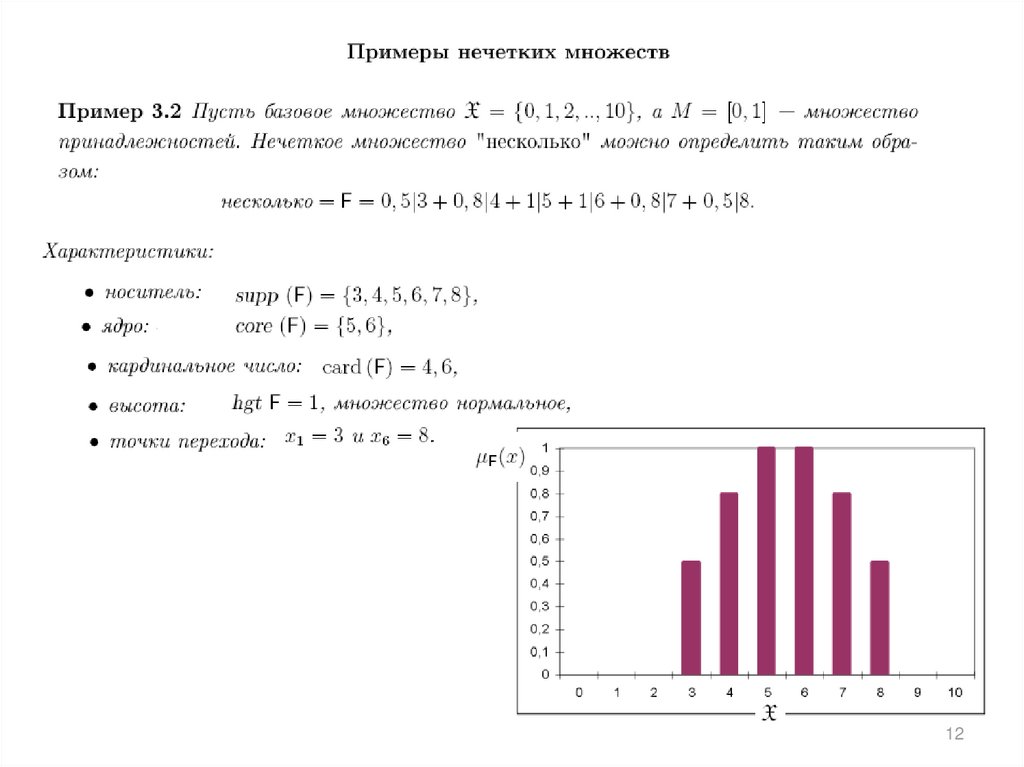
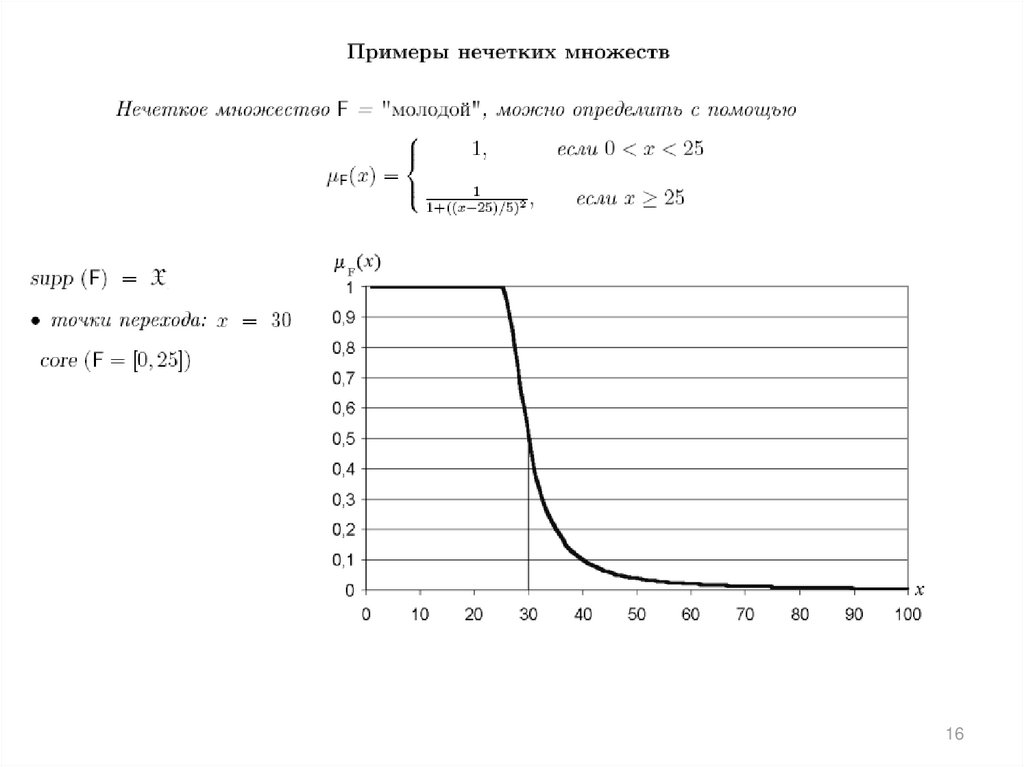
Характеристическая функция или индикатор множества
5

6.

6

7.

7

8.

8

9.

9

10.

10

11.

11

12.

12

13.

13

14.

14

15.

15

16.

16

17.

17

18.

18

19.

Отношения НМ
Включение:
19

20.

Отношения НМ
Эквивалентность:
20

21.

Операции над множествами
21

22.

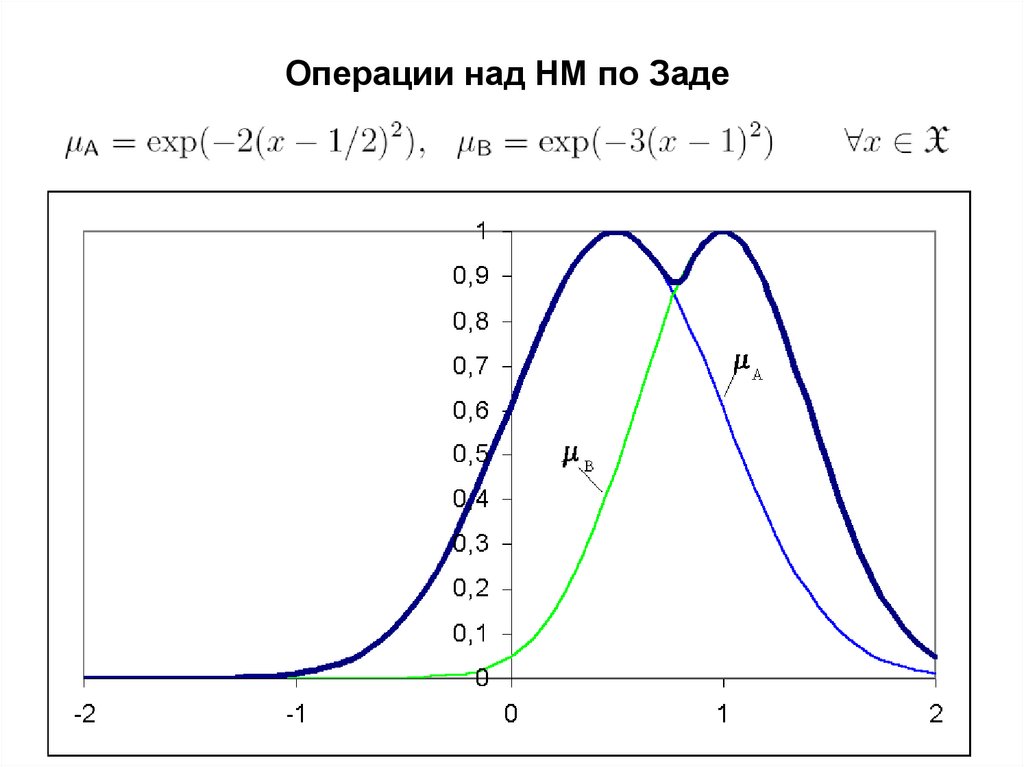
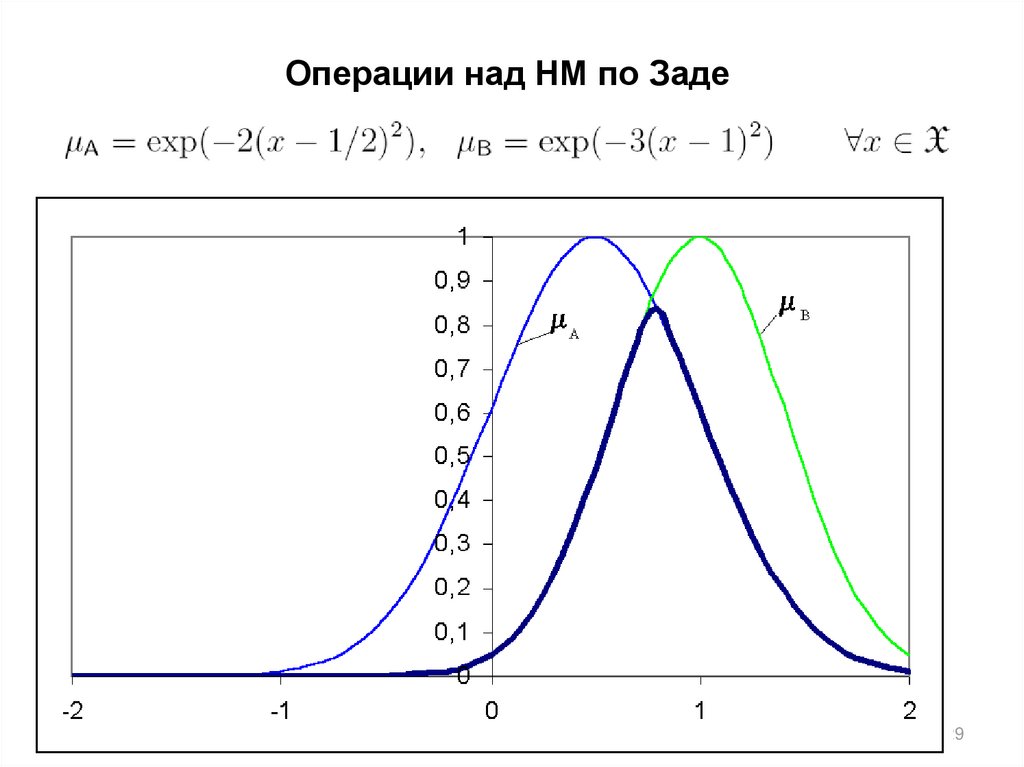
Операции над НМ по Заде
Дополнение НМ
22

23.

Операции над НМ по Заде
Дополнение НМ
23

24.

Операции над НМ по Заде
Объединение НМ
24

25.

Операции над НМ по Заде
Лемма
25

26.

Операции над НМ по Заде
26

27.

Операции над НМ по Заде
Пересечение НМ
27

28.

Операции над НМ по Заде
Лемма
28

29.

Операции над НМ по Заде
29

30.

Операции над НМ по Заде
Разность НМ
30

31.

Операции над НМ по Заде
31

32.

Операции над НМ по Заде
Дизъюнктивная сумма (Симметрическая разность) НМ
32

33.

Операции над НМ по Заде
33

34.

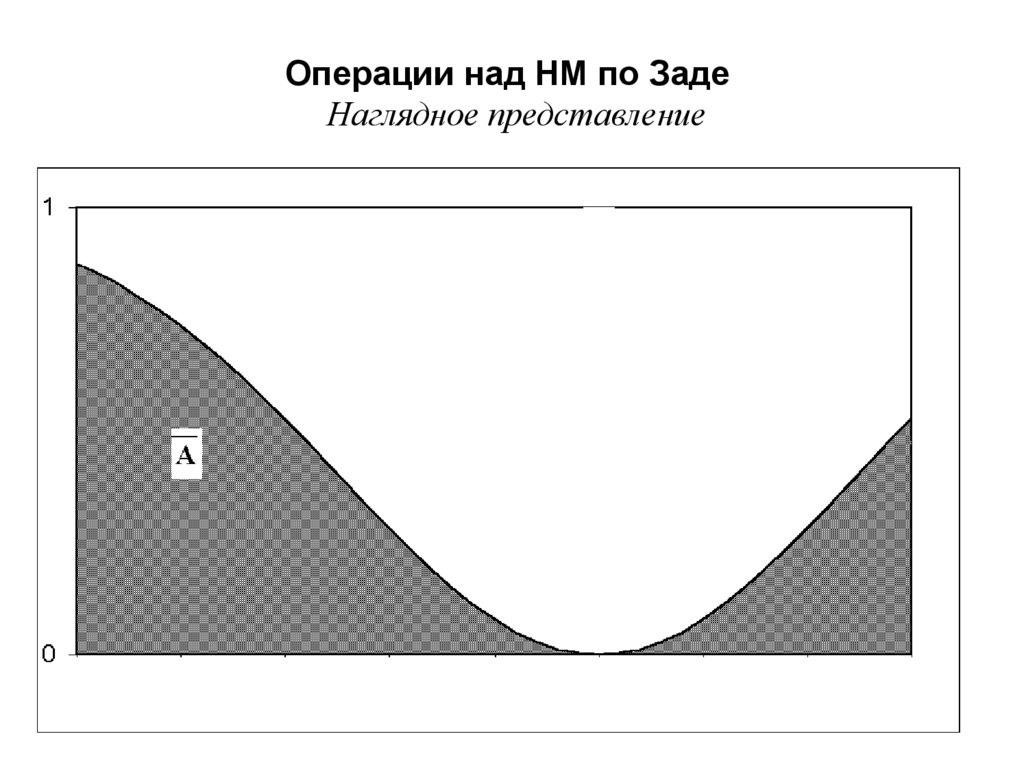
Операции над НМ по Заде
Наглядное представление
34

35.

Операции над НМ по Заде
Наглядное представление
35

36.

Операции над НМ по Заде
Наглядное представление
36

37.

Операции над НМ по Заде
Наглядное представление
37

38.

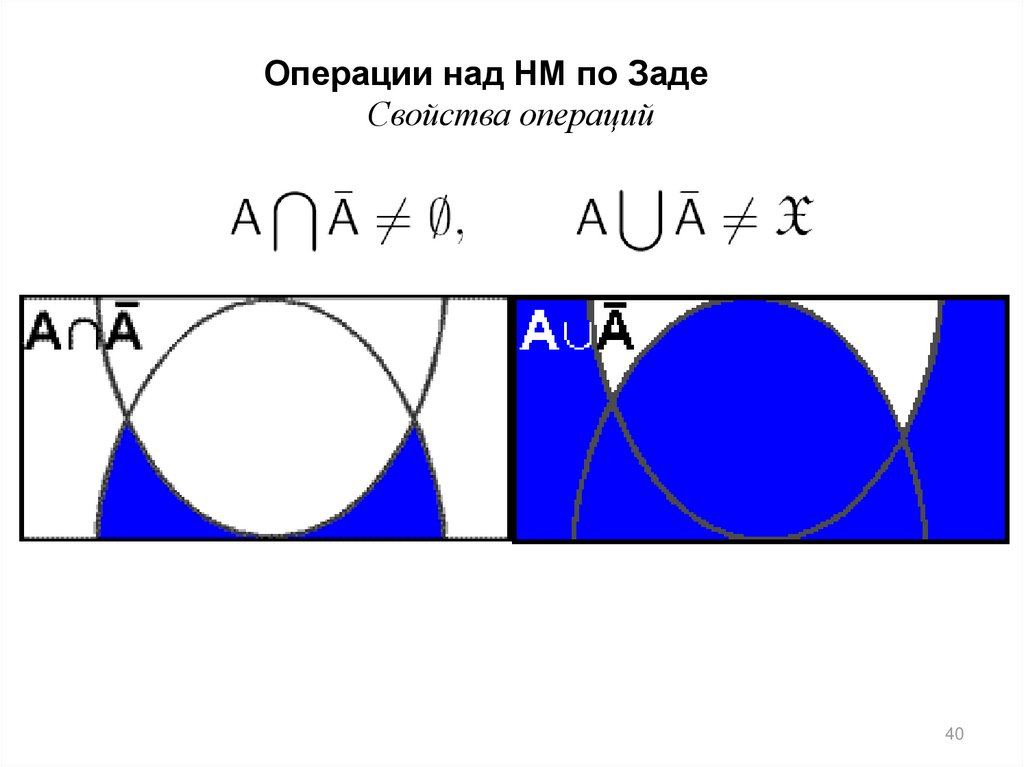
Операции над НМ по Заде
Свойства операций
38

39.

Операции над НМ по Заде
Свойства операций
39

40.

Операции над НМ по Заде
Свойства операций
40

41.

Операции над НМ по Заде
Возведение НМ в степень
41

42.

Операции над НМ по Заде
Произведение НМ на число
Выпуклая комбинация НМ
42

43.

Треугольная норма
(T1) –(T4)
Граничные условия:
43

44.

Треугольные нормы
Монотонность по обеим компонентам следует из (T3) и (T1)
44

45.

Треугольные конормы
(S1) –(S4)
Граничные условия:
45

46.

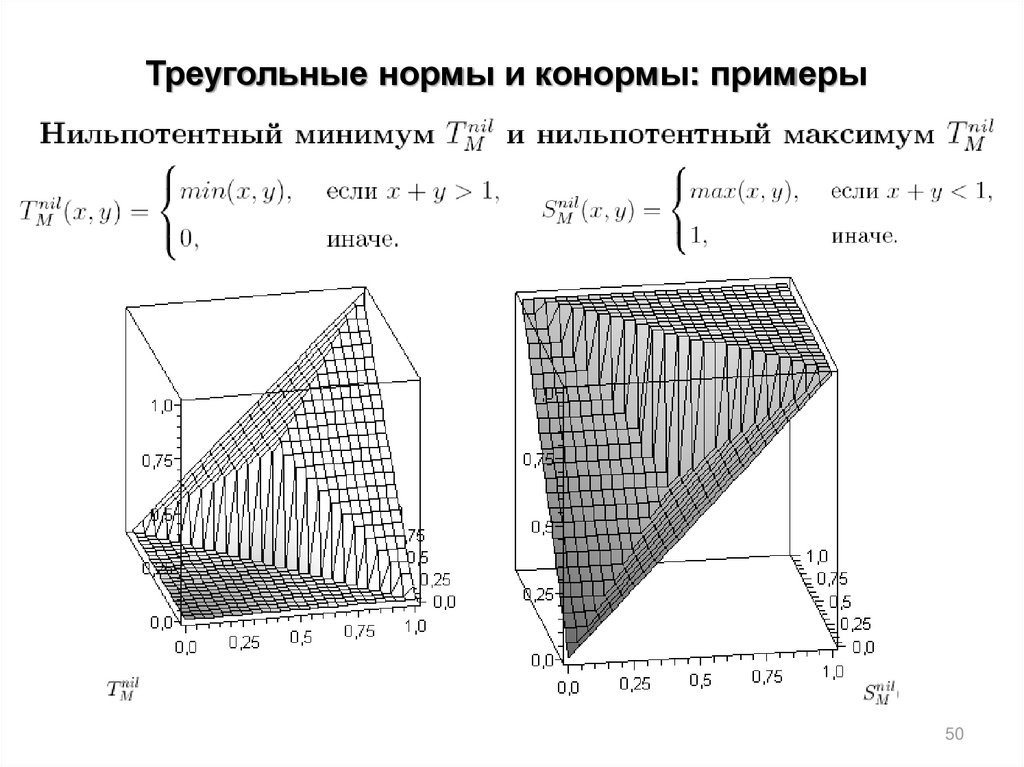
Треугольные нормы и конормы: примеры
46

47.

Треугольные нормы и конормы: примеры
47

48.

Треугольные нормы и конормы: примеры
48

49.

Треугольные нормы и конормы: примеры
49

50.

Треугольные нормы и конормы: примеры
50

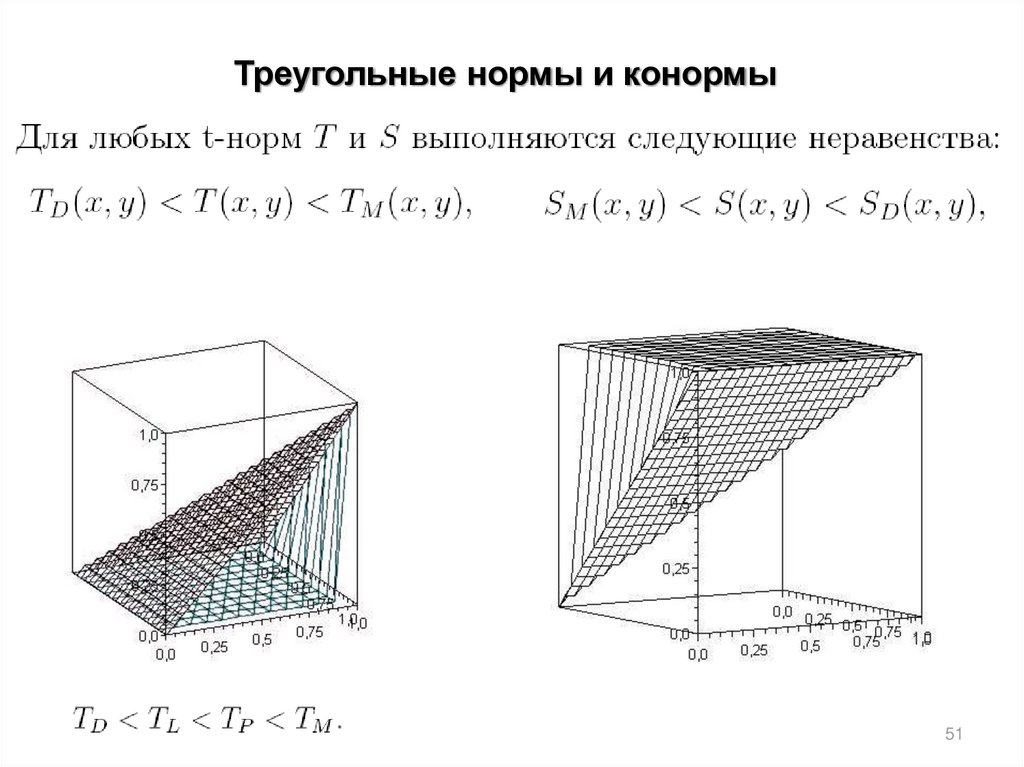
51.

Треугольные нормы и конормы
51

52.

Треугольные нормы и конормы
52

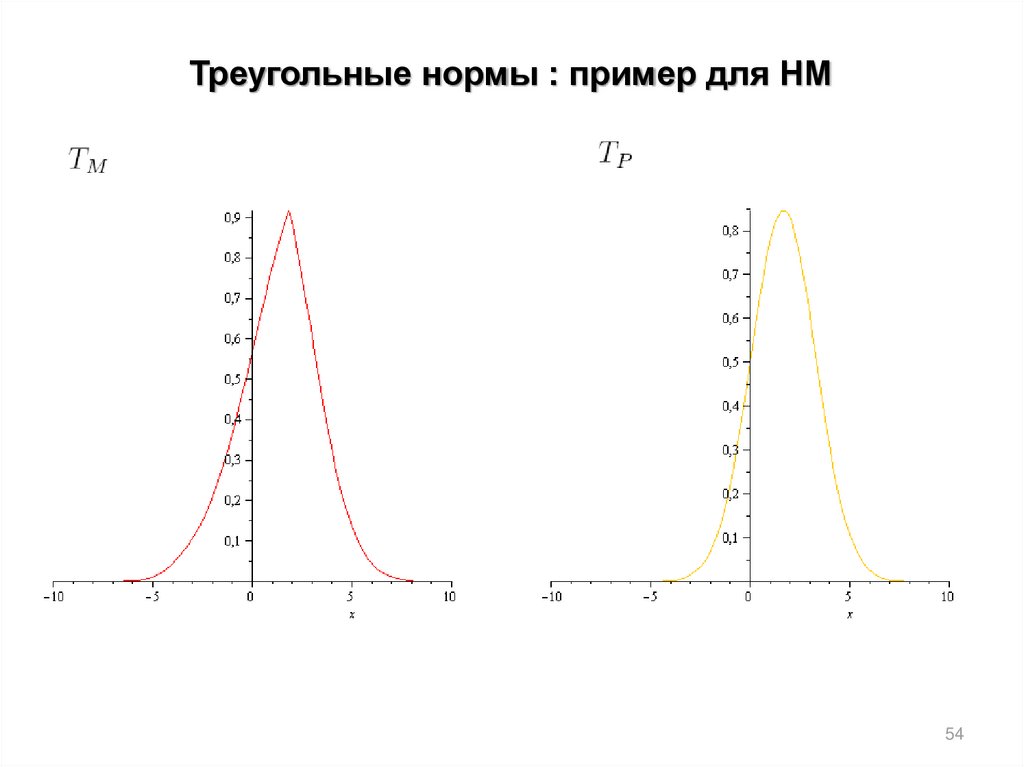
53.

Треугольные нормы : пример для НМ
53

54.

Треугольные нормы : пример для НМ
54

55.

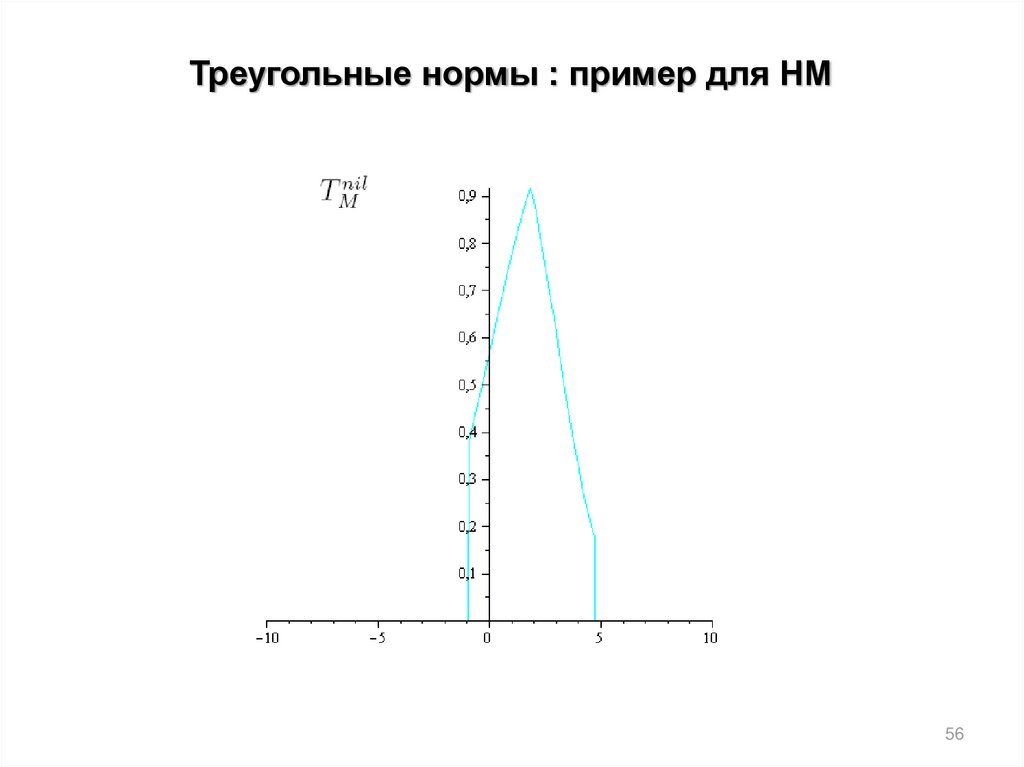
Треугольные нормы : пример для НМ
55

56.

Треугольные нормы : пример для НМ
56

57.

Треугольные нормы : пример для НМ
57

58.

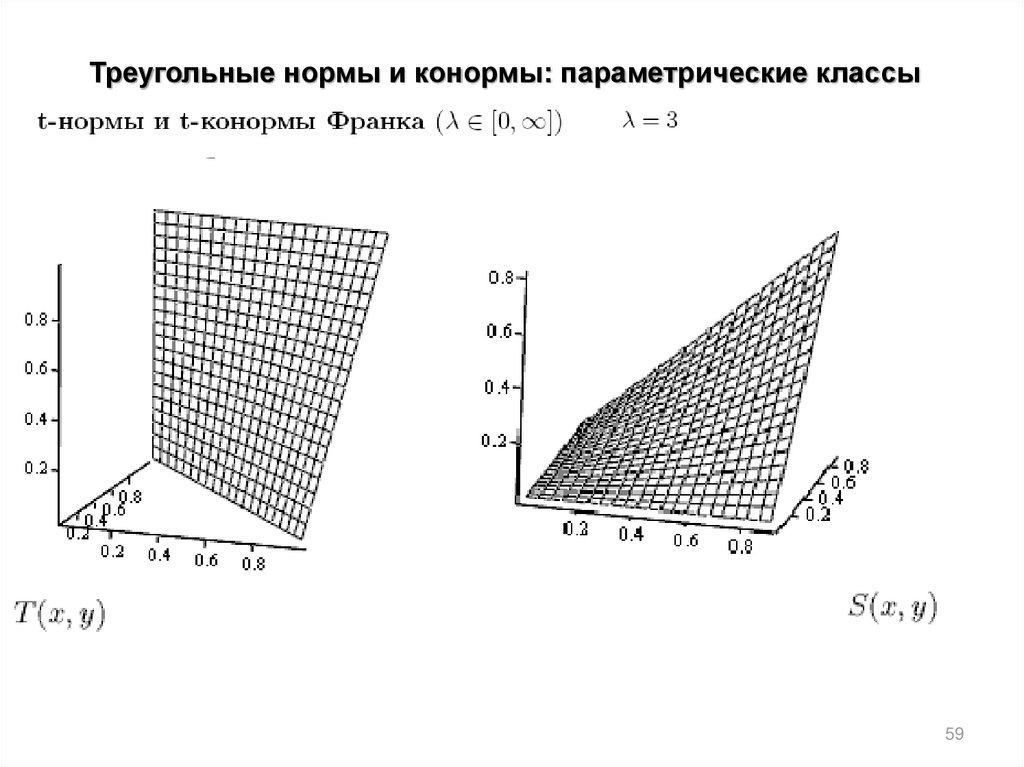
Треугольные нормы и конормы: параметрические классы
58

59.

Треугольные нормы и конормы: параметрические классы
59

60.

Треугольные нормы и конормы: параметрические классы
60

61.

Треугольные нормы и конормы: параметрические классы
61

62.

Треугольные нормы и конормы: параметрические классы
62

63.

Треугольные нормы и конормы: параметрические классы
63

64.

Отрицание
64

65.

Отрицание
Строгое
Квазистрогое
Типы отрицаний
Инволюция
Обычное
Слабое (интуиционисткое)
65

66.

Отрицание
m
классическое
Сугено, k = 3
квадратичное
66

67.

Тройки де Моргана

68.

Основные операции
Название
Пересечение
Объединение
Дополнение
Разность
Симметрическая разность
(дизъюнктивная сумма)
Степень НМ
Концентрирование (уплотнение)
Растяжение
Определение

69.

Основные операции
Название
Контрастная
интенсификация
Умножение на число
Выпуклая комбинация
Декартово
произведение
Оператор увеличения
нечеткости
Определение

70.

Степень НМ

71.

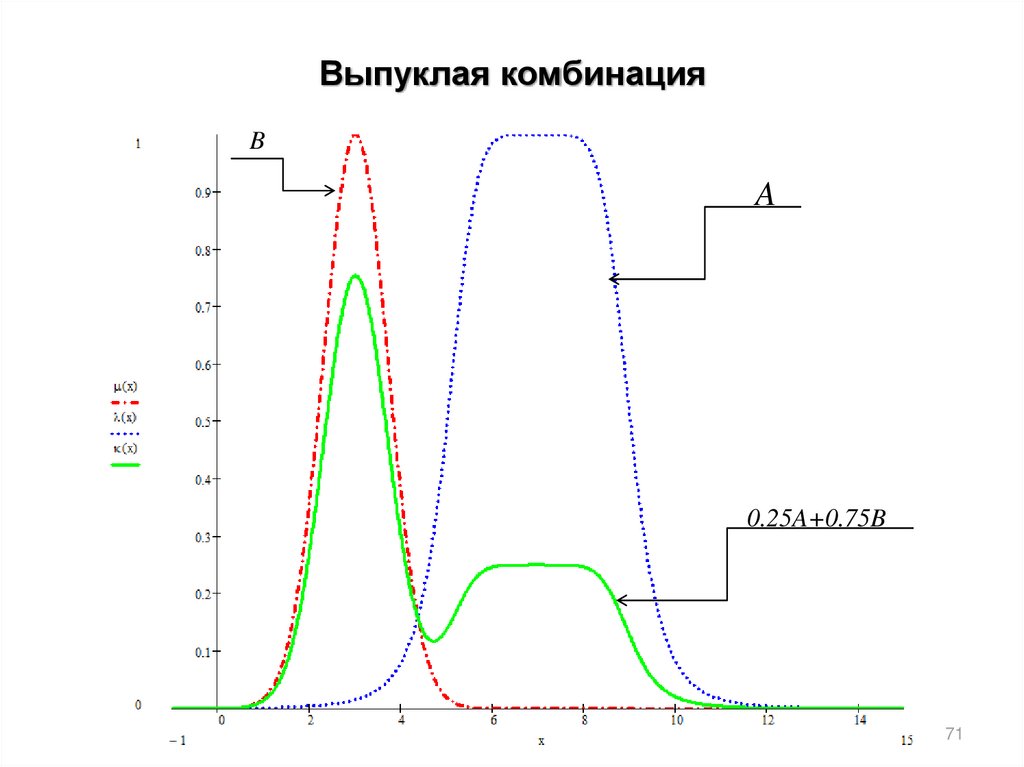
Выпуклая комбинация
B
A
0.25A+0.75B
71

72.

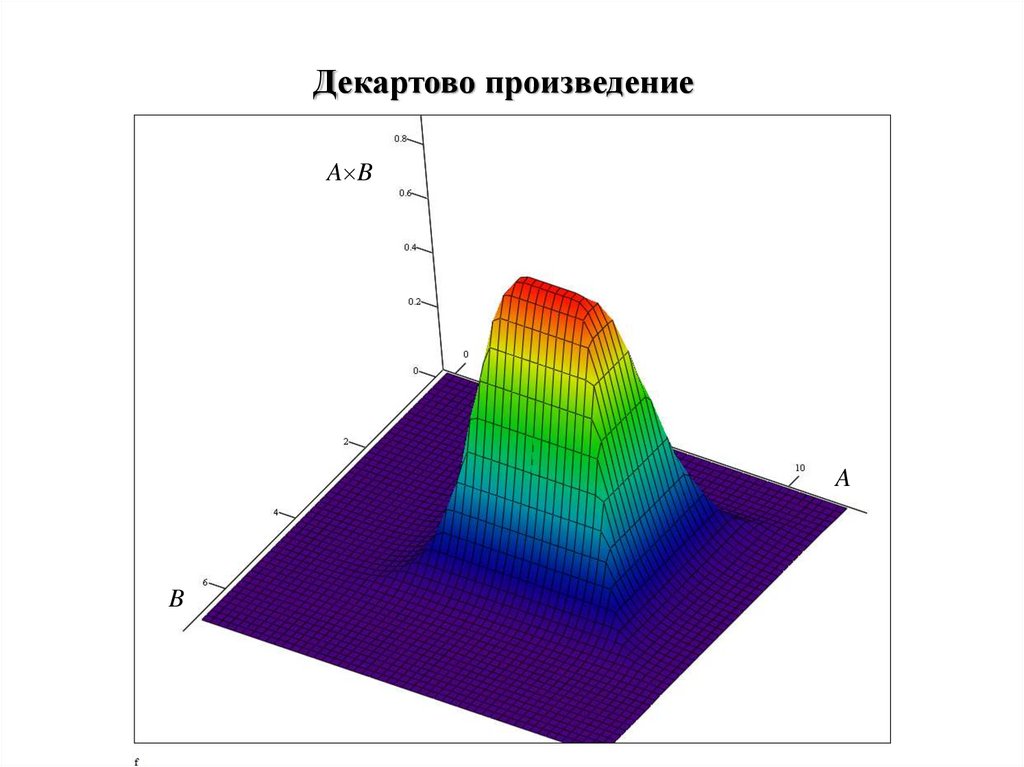
Декартово произведение
A B
A
B

73.

Оператор увеличения нечеткости

74.

Оператор увеличения нечеткости

75.

Множество уровня (сечение )

76.

Множество уровня (сечение )

77.

Множество уровня (сечение )
Сильное сечение
Слабое сечение
Свойства
Для
Для операций
по Заде
- любая выпуклая комбинация НМ
Tp
и Sp

78.

Теорема о декомпозиции
Доказательство

79.

Теорема о декомпозиции

80.

Теорема о декомпозиции: примеры
1.
2.

81.

Принцип обобщения Заде
Принцип обобщения как одна из основных идей теории
нечетких множеств носит эвристический характер и
позволяет расширить область определения исходного
отображения на класс нечетких множеств.
81

82.

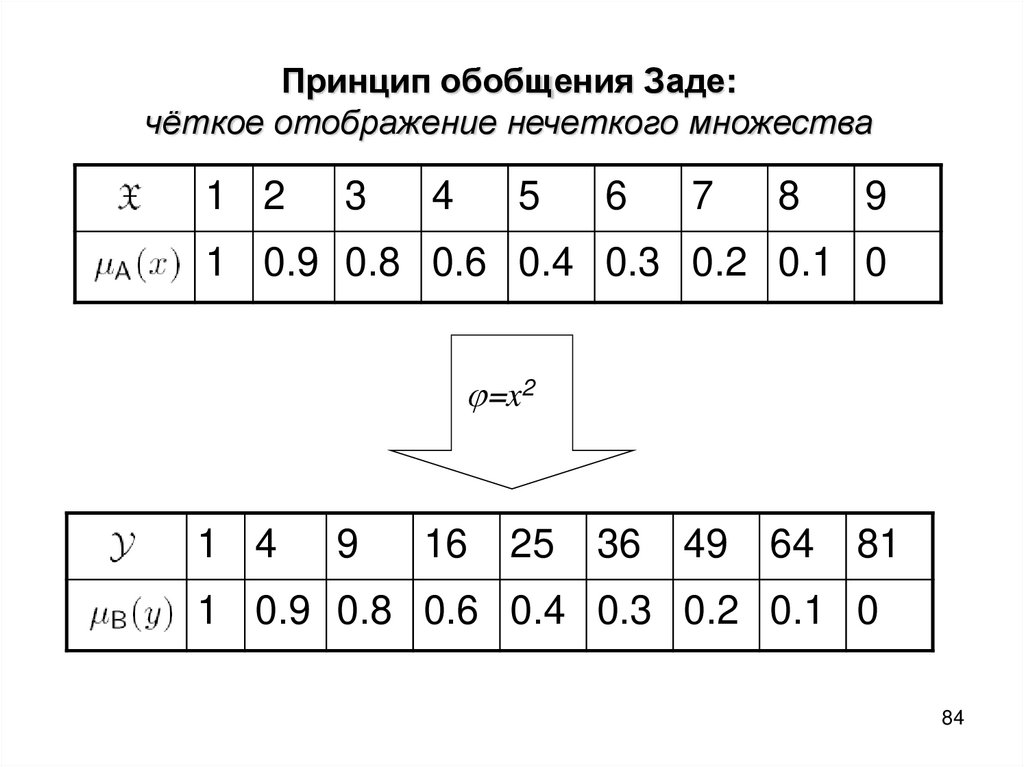
Принцип обобщения Заде:
чёткое отображение чёткого множества
Отображение множества
Значение
Образом множества
на множество
на элементе
при
:
называют образом элемента
отображении
называют множество
Прообраз
82

83.

Принцип обобщения Заде:
чёткое отображение нечеткого множества
- заданное чёткое отображение,
- некоторое нечеткое подмножество множества
принадлежности
В соответствии с принципом обобщения Заде образ
определяется как нечеткое подмножество множества
собой совокупность пар вида
где
с функцией
при отображении
, представляющее
функция принадлежности образа
где
83

84.

Принцип обобщения Заде:
чёткое отображение нечеткого множества
1 2
3
4
5
6
7
8
9
1 0.9 0.8 0.6 0.4 0.3 0.2 0.1 0
=x2
1 4
9
16
25
36
49
64
81
1 0.9 0.8 0.6 0.4 0.3 0.2 0.1 0
84

85.

Принцип обобщения Заде:
чёткое отображение нечеткого множества
-4
-3
-2
-1
0 1
2
3
4
0.1 0.3 0.5 0.6 1 0.9 0.7 0.2 0.1
=x2
0
1
4
9
16
{0}
{-1, 1}
{-2, 2}
{-3, 3}
{-4, 4}
1
0.9
0.7
0.3
0.1
85

86.

Принцип обобщения Заде:
чёткое отображение нечеткого множества
1
0.8
0.6
m ( x)
0.4
0.2
0
1
1
0.5
0
0.5
1
x
1.5
2
2.5
3
3
86

87.

Принцип обобщения Заде:
чёткое отображение нечеткого множества
x
( x)
2
1.5
1.5
1
( x)
0.5
0
1
1
0.5
0
0.5
1
x
1.5
2
2.5
3
3
87

88.

Принцип обобщения Заде:
чёткое отображение нечеткого множества
1
0.8
0.6
y ( x)
0.4
0.2
0
0
0
0
0.5
1
1.5
x
2
2.5
3
3
88

89.

Принцип обобщения Заде:
чёткое отображение нечеткого множества
1
0.8
0.6
y ( x)
m ( x)
0.4
0.2
0
0
1
0 1
0.5
0
0.5
1
x
1.5
2
3
2.5
3
89

90.

Принцип обобщения Заде:
нечёткое отображение чёткого множества
Нечеткое отображение можно описать как отображение
котором элементу
ставится в соответствие
не конкретный элемент множества
а нечеткое подмножество
, при
,
.
90

91.

Принцип обобщения Заде:
нечёткое отображение чёткого множества
Функция
при фиксированном
есть функция принадлежности нечеткого множества
в
, представляющего собой нечеткий образ элемента
при данном отображении
Образом четкого множества
отображении
.
при нечетком
будет объединение образов его элементов:
91

92.

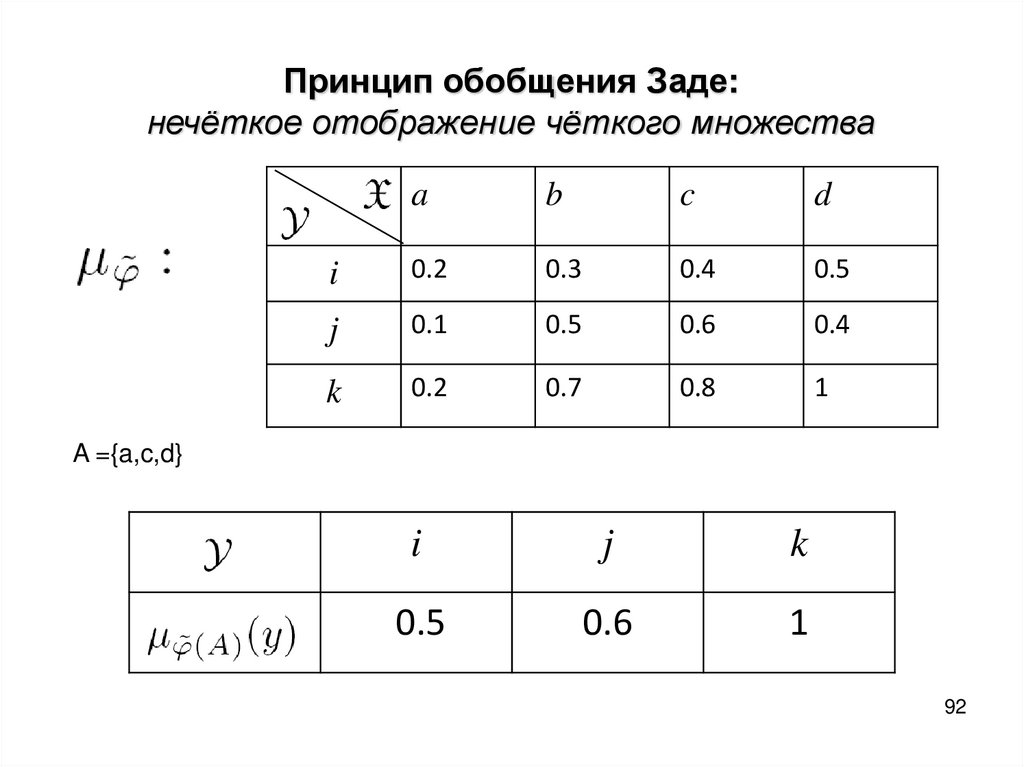
Принцип обобщения Заде:
нечёткое отображение чёткого множества
a
b
c
d
i
0.2
0.3
0.4
0.5
j
0.1
0.5
0.6
0.4
k
0.2
0.7
0.8
1
y
A ={a,c,d}
i
j
k
0.5
0.6
1
92

93.

Принцип обобщения Заде:
нечёткое отображение чёткого множества
y
93

94.

Принцип обобщения Заде:
нечёткое отображение чёткого множества
Образ точки x=2
94

95.

Принцип обобщения Заде:
нечёткое отображение чёткого множества
Образ множества [-1,1]
95

96.

Принцип обобщения Заде:
нечёткое отображение нечёткого множества
Пусть
- заданное нечеткое отображение,
- заданное нечеткое множество в
.
В соответствии с принципом обобщения Заде образ
отображении
где
при
определяется как совокупность пар вида
при каждом фиксированном
представляет собой нечеткое подмножество множества
96

97.

Принцип обобщения Заде:
нечёткое отображение нечёткого множества
Образом нечеткого множества
отображении
при нечетком
будет объединение образов его элементов:
97

98.

Принцип обобщения Заде:
нечёткое отображение нечёткого множества
a
b
c
d
i
0.2
0.3
0.4
0.5
j
0.1
0.5
0.6
0.4
k
0.2
0.7
0.8
1
y
a
b
c
1
0.8 0.5
d
0.2
i
j
k
0.4
0.5
0.7
98

99.

Принцип обобщения Заде:
нечёткое отображение нечёткого множества
y
99

100.

Принцип обобщения Заде:
нечёткое отображение нечёткого множества
100

101.

Принцип обобщения Заде:
нечёткое отображение нечёткого множества
Образ нечеткого множества
101

102.

Принцип обобщения Заде:
нечёткое отображение нечёткого множества
Нечеткое множество и его образ
102

103.

Принцип обобщения Заде:
прообраз нечёткого множества
Прообразом
нечеткого множества
в
при нечетком отображении
называется объединение всех нечетких множеств,
образы которых при этом отображении принадлежат
(являются подмножествами) множеству
.
103

104.

Принцип обобщения Заде:
прообраз нечёткого множества
104

105.

Принцип обобщения Заде:
прообраз нечёткого множества
Теорема. Пусть
Тогда прообраз
отображении
нечеткого множества
в
при нечетком
описывается функцией принадлежности
105

106.

Принцип обобщения Заде:
прообраз нечёткого множества
106

107.

Принцип обобщения Заде:
прообраз нечёткого множества
A
B
u
0.1
0.3
v
0.7
0.8
w
0.3
0.6
z
0.5
0.6
C
D
0.5
0.6
0.9
0.6
0.9
1
0.5
0.9
u
0.4
v
0.7
w
0.9
z
1
107

108.

Принцип обобщения Заде:
прообраз нечёткого множества
={(C,u), (D,u), (B,v), (C,v), (D,w)}
NA =
NB ={v}
NC ={u,v}
ND ={u,w}
={B, C, D}
108

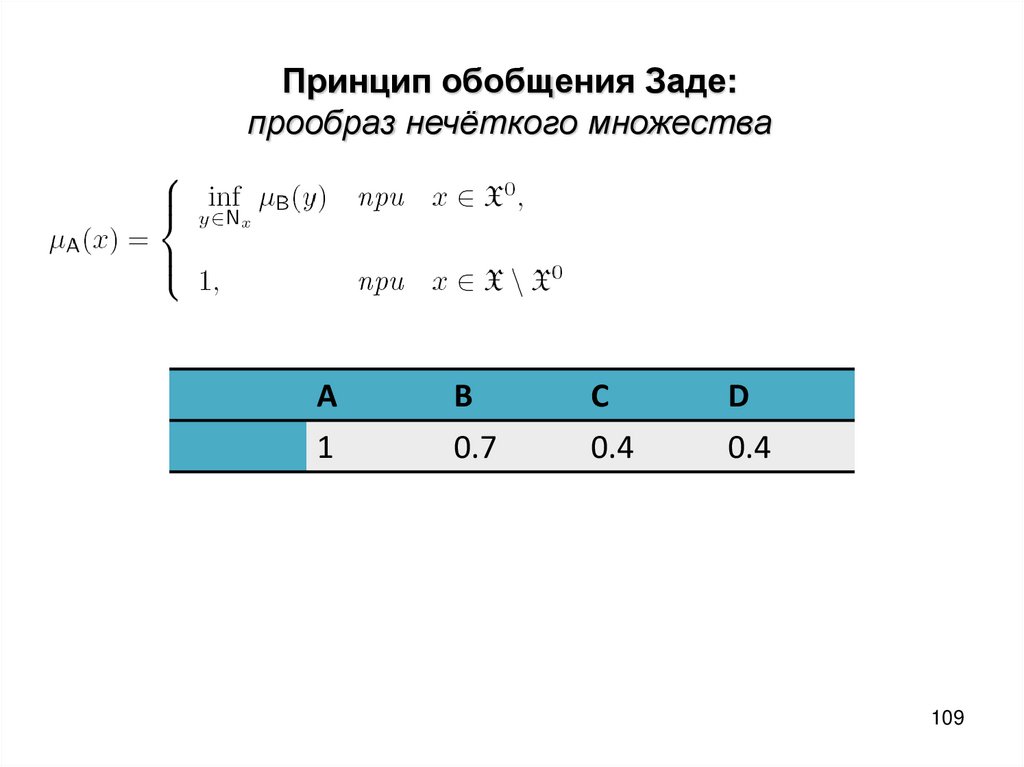
109.

Принцип обобщения Заде:
прообраз нечёткого множества
A
1
B
0.7
C
0.4
D
0.4
109

110.

Принцип обобщения Заде:
прообраз нечёткого множества
110

111.

Принцип обобщения Заде:
прообраз нечёткого множества
111

112.

Принцип обобщения Заде:
прообраз нечёткого множества
112

113.

Принцип обобщения Заде:
прообраз нечёткого множества
113

114.

Показатель размытости: подходы к определению
1. Интерпретация как показателя внутренней
неопределенности, двусмысленности,
противоречивости, обусловленных неполной,
частичной принадлежностью объектов множеству.
2. Интерпретация как меры отличия нечеткого
множества от обычного множества.
3. Существование нетривиального показателя
размытости, удовлетворяющего определенным
свойствам, напрямую зависит от свойств алгебры
нечетких множеств и характеризует ее как
алгебраическую структуру.
114

115.

Показатель размытости: подходы к определению
A. De Luca, S. Termini, A definition of a non-probabilistic
entropy in the setting of fuzzy sets theory, Information and
Control 20 (1972) 301–312
Bart Kosko, Fuzzy Entropy and Conditioning, Information
Sciences 40 (1986) 165–174
S. Al-Sharhan, F. Karray, W. Gueaieb, O. Basir, Fuzzy
entropy: a brief survey // The 10th IEEE International
Conference on Fuzzy Systems, 2001. Vol. 3 (S. l., 2001)
1135–1139.
115

116.

Аксиоматический подход
к определению показателя размытости нечеткого множества
Аксиомы Де Луки и Термини:
1. энтропия равна 0 только для четкого множества;
2. энтропия максимальна при значениях функций
принадлежности 0,5;
3. для более нечеткого множества энтропия всегда
больше, чем для менее нечеткого;
4. для нечеткого множества и его дополнения (отрицания)
энтропия одинакова.
116

117.

Аксиоматический подход
к определению показателя размытости нечеткого множества
Глобальный показатель размытости нечеткого множества
определим
в виде функционала , удовлетворяющего следующим условиям:
Показатель размытости - аддитивный, симметричный и строго возрастающий с
увеличением размытости нечеткого множества функционал, определенный на
множестве
всех нечетких подмножеств множества
117

118.

Аксиоматический подход
к определению показателя размытости нечеткого множества
Утверждение. Вещественный, определенный на
функционал является
показателем размытости тогда и только тогда, если он допускает
представление
где
вещественнозначные функции от
строго возрастает на интервале
множества
.
и
такие, что
— число элементов
118

119.

Аксиоматический подход
к определению показателя размытости нечеткого множества
Логарифмическая энтропия нечетких множеств
где
— функция Шеннона
119

120.

Метрический подход
к определению показателя размытости нечеткого множества
Метрика – функция расстояния.
1. Аксиома тождества
2. Аксиома неотрицательности
3. Аксиома симметричности
4. Неравенство треугольника
120

121.

Метрический подход
к определению показателя размытости нечеткого множества
Виды расстояний между нечеткими множествами
Формула
Область
значений
Хемминга
(линейное)
Евклидово
(квадратичное)
Относительное
расстояние
Хемминга
Относительное
евклидово
расстояние
121

122.

Метрический подход
к определению показателя размытости нечеткого множества
Множеством, ближайшим к нечеткому множеству
множество
такое, что
, называется обычное
Максимально размытое множество
122

123.

Метрический подход
к определению показателя размытости нечеткого множества
Метрический показатель размытости
мера отличия нечеткого множества от ближайшего к нему
обычного множества;
расстояние до максимального размытого множества
расстояние между нечетким множеством и его дополнением.
123