Similar presentations:
Оптимизация. Функция одной переменной. Определение локального экстремума. Классификация локального экстремума
1.
ОптимизацияГде же максимум?
Лукьянченко Петр Павлович
2.
Знакомство>10 лет преподавания в НИУ-ВШЭ
>3 лет – Quantitative Research (UFG, UBS)
>6 лет – Data Science (Retail, Госсектор)
Учился в London School of Economics,
University College London
Специализация:
Численные
методы
решения уравнений. Функциональные
языки программирования
2
3.
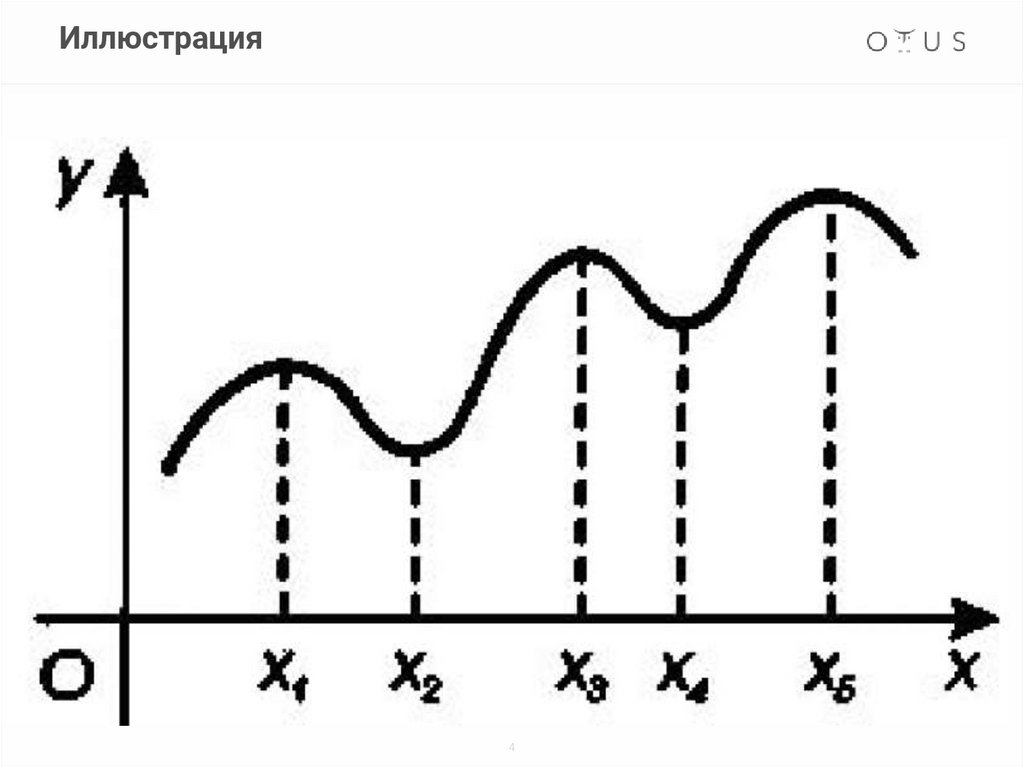
Функция одной переменнойОпределение Локального экстремума
Классификация Локального экстремума
Если вторая производная в точке экстремума положительная, то это точка локального
минимума.
Если вторая производная в точке экстремума отрицательная, то это точка локального
максимума.
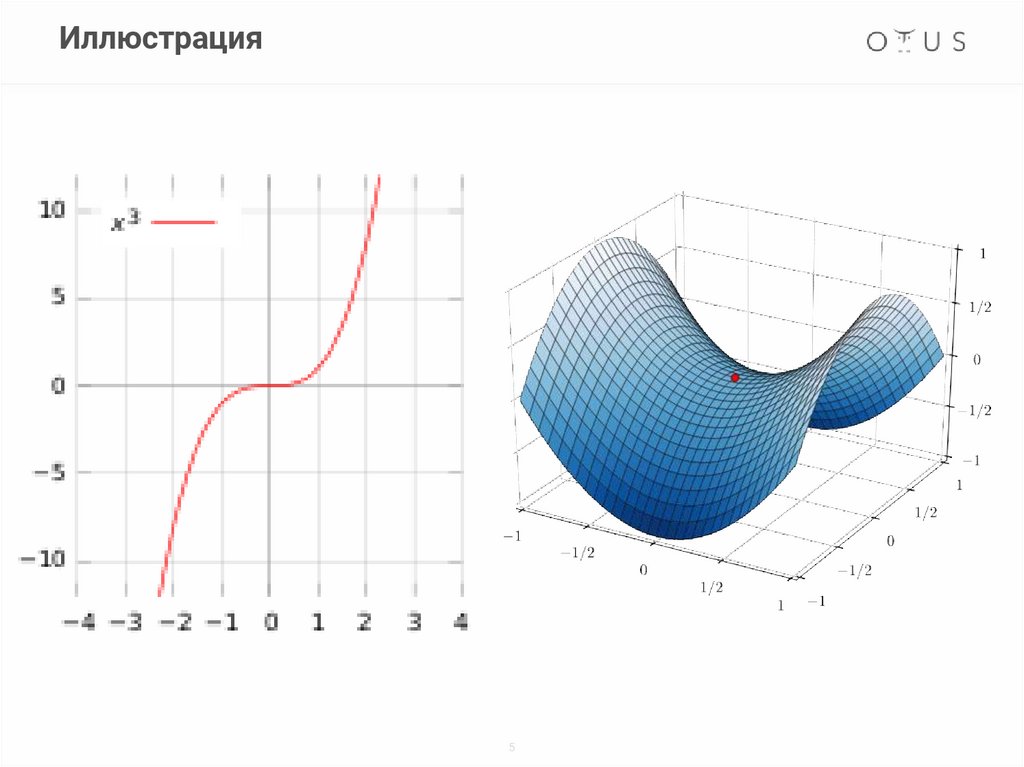
Если вторая производная равна нулю, тогда ?
3
4.
Иллюстрация4
5.
Иллюстрация5
6.
ПримерыВычислить максимум/минимум данных функций:
Вычислить максимум/минимум функции
на интервале
6
7.
Численные методыМетод перебора
N.B. Метод перебора (расширенный)
Домашнее задание:
7
8.
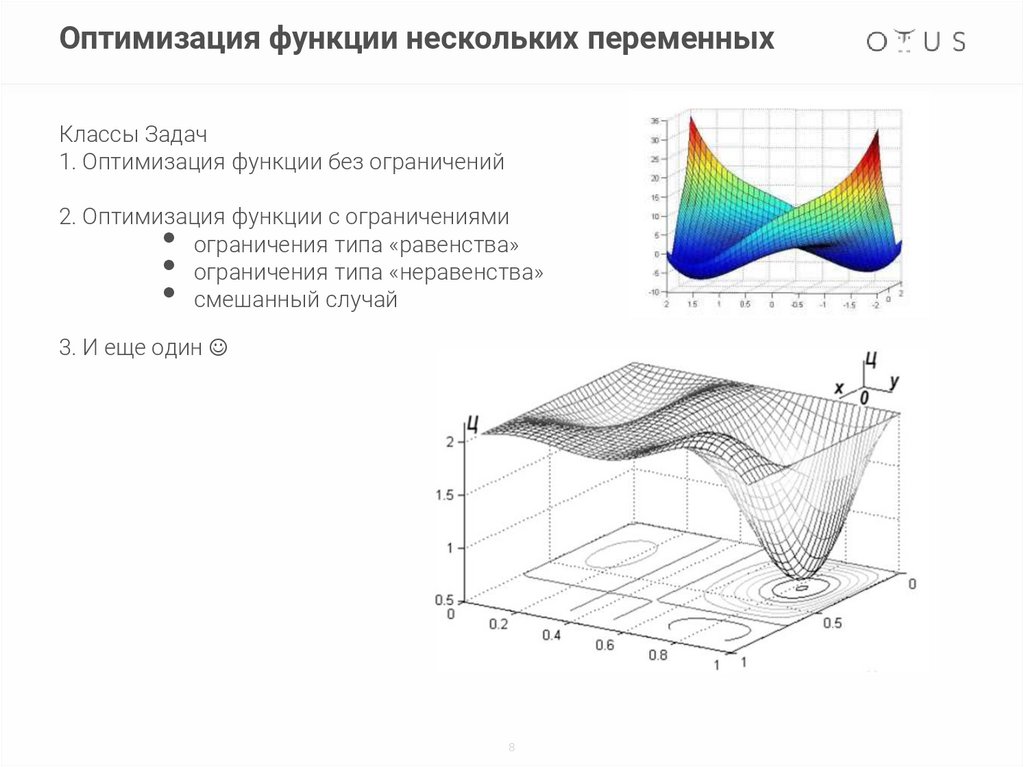
Оптимизация функции нескольких переменныхКлассы Задач
1. Оптимизация функции без ограничений
2. Оптимизация функции с ограничениями
ограничения типа «равенства»
ограничения типа «неравенства»
смешанный случай
3. И еще один
8
9.
Оптимизация функции без ограниченийОпределение Локального экстремума
Классификация Локального экстремума
9
10.
Оптимизация функции без ограниченийНайдите критические точки и классифицируйте их:
пример 1.
пример 2.
Домашнее задание:
Найдите критические точки функции:
10
11.
Оптимизация функции c ограничениямиАлгоритм:
1. Построить функцию Лагранжа
2. Найти критические точки функции Лагранжа
3. Классифицировать их с помощью матрицы Гессе (окаймленной)
матрица Гессе
окаймленная матрица Гессе
без ограничений
с ограничениями
11
12.
Оптимизация функции c ограничениями(равенства)
Найдите экстремумы функции
Найдите экстремумы функции
12
13.
Оптимизация функции c ограничениями(неравенства)
Найдите экстремумы функции при ограничении типа неравенство
13
14.
3-й класс задач ОптимизацииНайдите максимальное значение Линейной функции при Линейных ограничениях
14
15.
Линейное программированиеК задачам линейного программирования относятся задачи поиска экстремумов
линейных функций при линейных ограничениях.
Общая постановка задачи
15
16.
Методы решения№
Случай
Метод решения
1
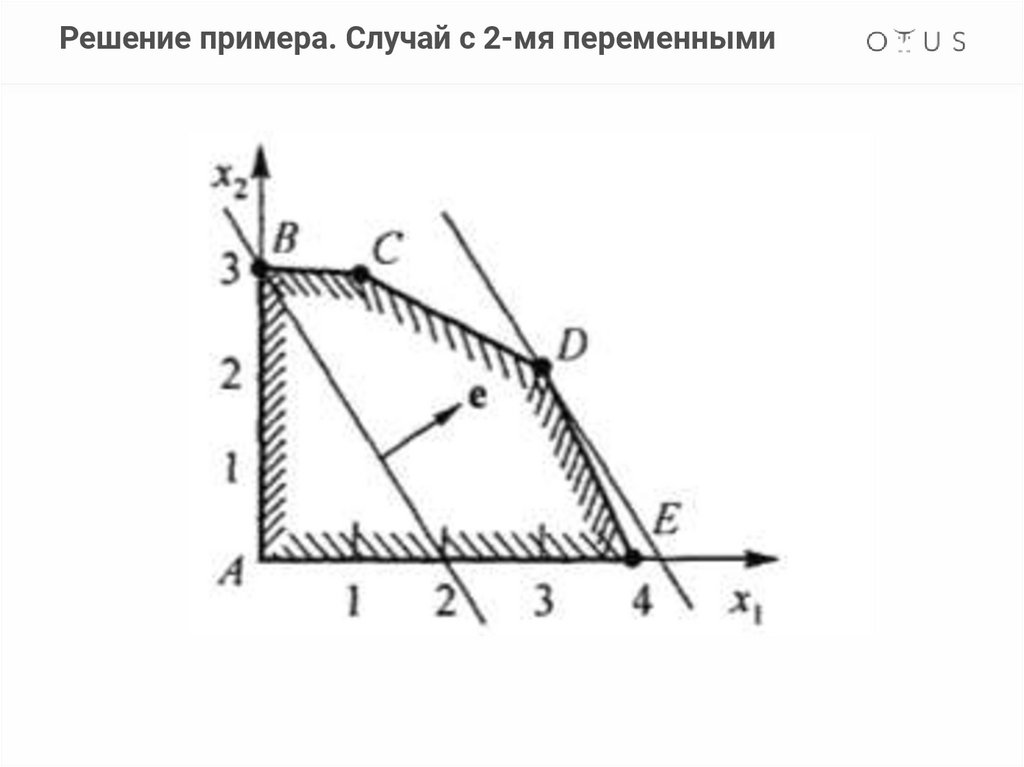
Случай с 2-мя
переменными
Графические способ решения
2
Случай с 2 ограничениями
«Теорема двойственности +
Графические способ решения»
3
Остальные
Симплекс-Метод
Пример:
16
17.
Решение примера. Случай с 2-мя переменными18.
Теорема двойственности18
19.
Спасибо за внимание!Лукьянченко Петр















 mathematics
mathematics








