Строение атома

1.

СТРОЕНИЕ АТОМА

2.

СТРОЕНИЕ АТОМА
РАДИОАКТИВНОСТЬ
При изучении электронной структуры атомов нет
необходимости запоминать полные электронные
конфигурации атомов всех элементов.
Важно ориентироваться в ПСЭ. Например, нужно
знать расположение s-, p-, d-,f-элементов, принципы
заполнения
электронных
оболочек
атомов,
изменение свойств атомов элементов по группам и
периодам.

3.

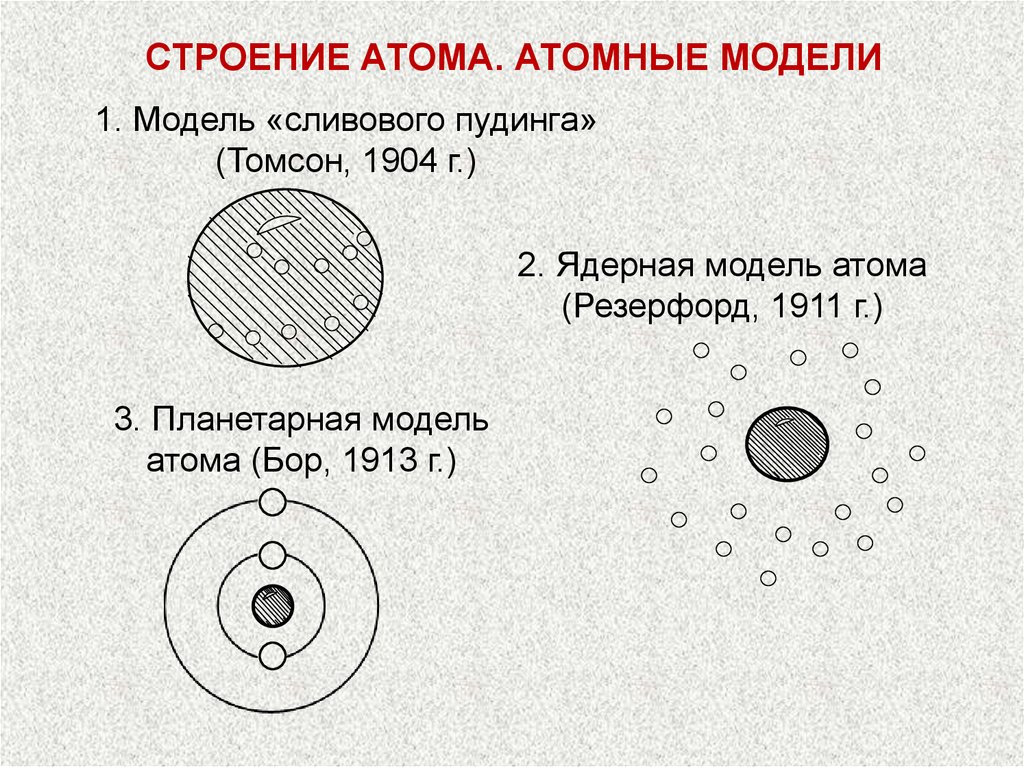
СТРОЕНИЕ АТОМА. АТОМНЫЕ МОДЕЛИ
1. Модель «сливового пудинга»
(Томсон, 1904 г.)
2. Ядерная модель атома
(Резерфорд, 1911 г.)
3. Планетарная модель
атома (Бор, 1913 г.)

4.

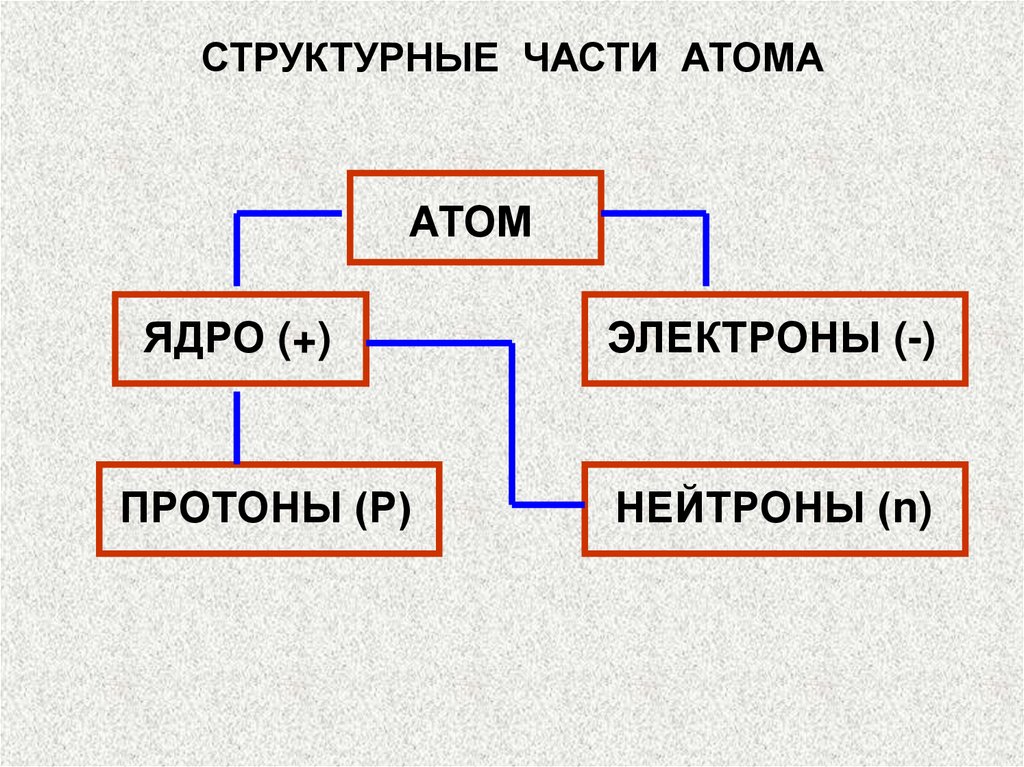
СТРУКТУРНЫЕ ЧАСТИ АТОМА
АТОМ
ЯДРО (+)
ПРОТОНЫ (Р)
ЭЛЕКТРОНЫ (-)
НЕЙТРОНЫ (n)

5.

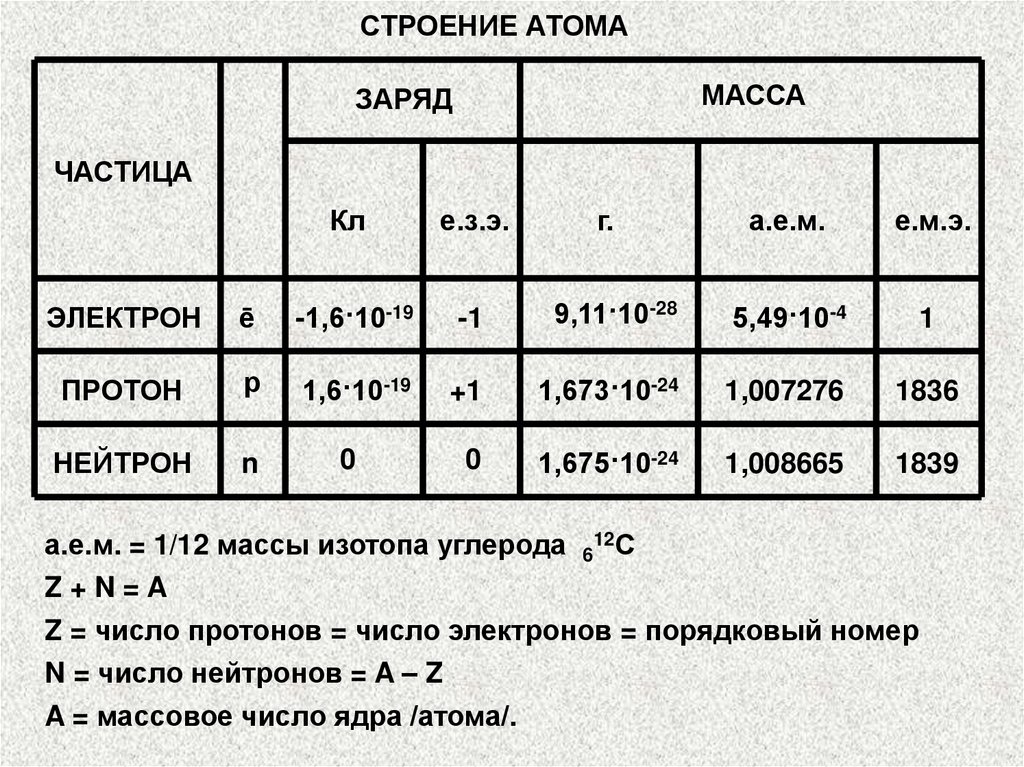
СТРОЕНИЕ АТОМА
МАССА
ЗАРЯД
ЧАСТИЦА
Кл
е.з.э.
г.
а.е.м.
е.м.э.
ЭЛЕКТРОН
ē
-1,6·10-19
-1
9,11·10-28
5,49·10-4
1
ПРОТОН
р
1,6·10-19
+1
1,673·10-24
1,007276
1836
НЕЙТРОН
n
0
1,675·10-24
1,008665
1839
0
а.е.м. = 1/12 массы изотопа углерода 612С
Z+N=A
Z = число протонов = число электронов = порядковый номер
N = число нейтронов = A – Z
A = массовое число ядра /атома/.

6.

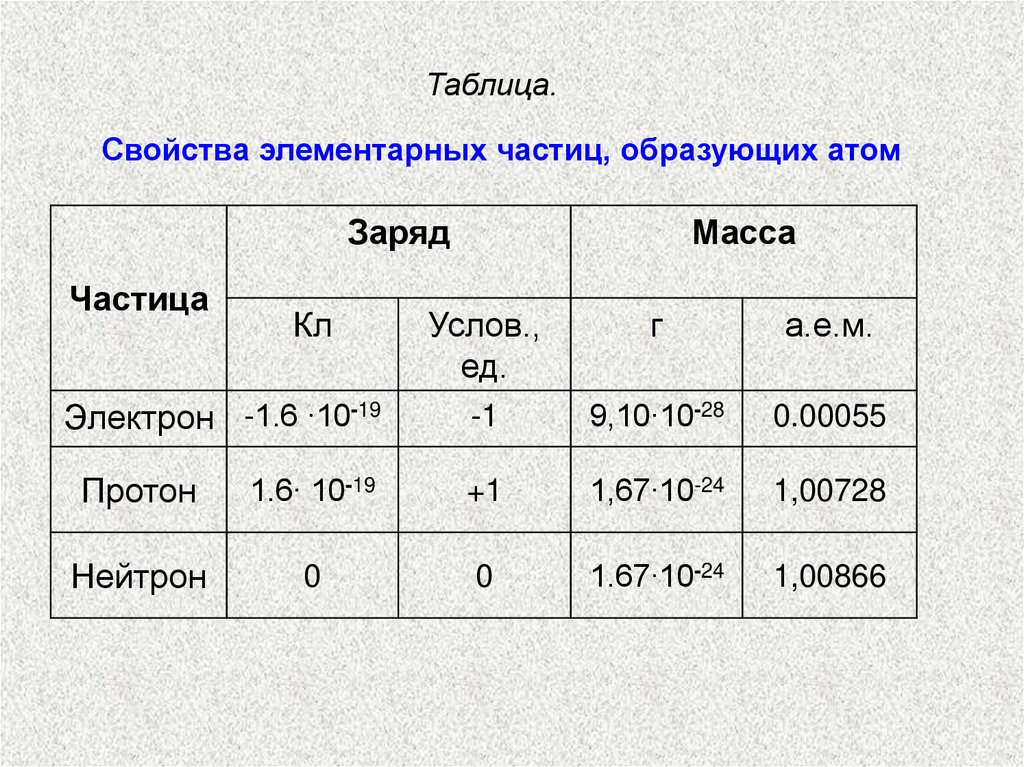
Таблица.
Свойства элементарных частиц, образующих атом
Заряд
Частица
Кл
Электрон -1.6 ∙10-19
Масса
Услов.,
ед.
г
а.е.м.
-1
9,10∙10-28
0.00055
Протон
1.6∙ 10-19
+1
1,67∙10-24
1,00728
Нейтрон
0
0
1.67∙10-24
1,00866

7.

МОДЕЛЬ АТОМА БОРА (1913 Г.)
Обоснованием планетарной и более поздних электронных моделей атома служат главным образом атомные
спектры и данные по энергии ионизации атомов.
АТОМНЫЕ СПЕКТРЫ
Всякий спектр представляет собой развертку, разложение
излучения на его компоненты. Ниже показан полный спектр
электромагнитного излучения:
Гаммалучи
10-5
Рентгеновские
лучи
10-3
1
Видимый (400-800 нм)
свет
МКВУФ
ИФК
излучение
лучи
лучи
103
10
105
Длина волны λ, нм
107
Радиоволны
109

8.

НЕПРЕРЫВНЫЕ И ДИСКРЕТНЫЕ СПЕКТРЫ
ИЗЛУЧЕНИЯ
1. Непрерывный (сплошной) спектр - Это
спектр, содержащий излучение со всеми
длинами
волн
в
пределах
некоторого
диапазона. Примером сплошного спектра является
видимый свет.
2. Дискретный спектр – это спектр, в котором
недостает
излучения
с
определенными
длинами волн. Примером такого спектра
является атомный спектр поглощения (или
испускания).

9.

НЕПРЕРЫВНЫЕ И ДИСКРЕТНЫЕ СПЕКТРЫ
ИЗЛУЧЕНИЯ
Если пучок белого света пропустить через
газообразный образец какого-либо элемента, то в
прошедшем через образец пучке света будет
недоставать излучения с определенными длинами
волн. Спектр такого излучения называется
атомным
спектром
поглощения.
При
нагревании газообразного образца до высок. темп.
Он будет испускать излучение с определенными
длинами волн - атомный спектр испускания.

10.

Постулаты Бора
2.1.
m·V·r = n·(h/2π) – квантовый момент
2.2.
h·ν = Е2 – Е1 – переход электрона с
количества движения
орбиты на орбиту

11.

УТВЕРЖДЕНИЯ БОРА
Объясняя дискретный характер атомных спектров
поглощения или испускания, Бор предположил, что между
линиями атомного спектра и энергиями электронов в
атомах существует соответствие.
Он утверждал, что электрон в атоме не может иметь
произвольных
значений
энергии
в
диапазоне
непрерывного изменения, а должен иметь только
определенные фиксированные значения энергии.
Эти значения энергии Бор назвал дискретными, или
квантовыми уровнями. Каждому такому значению
энергии Бор приписал определенное число, которое он
назвал квантовым числом.

12.

УРАВНЕНИЯ, ПОЛУЧЕННЫЕ БОРОМ
Воспользовавшись определениями кинетической
энергии частицы (К.Э. = mV2/2) и потенциальной
энергии электрона (П.Э. = –е2/r), Бор получил следующие уравнения:
n2
r =
1
λ
=
h2
Е =–
4π2me4
К
1
he
n2
–
1
m2
;
Ron = 1,0968·107 м-1
R =
К
n2
; К=
h2
n = 1, 2, 3, 4 …
2π2me4
К
he
2π2me4
=
h3·e
=
= 1,0978·107 м-1

13.

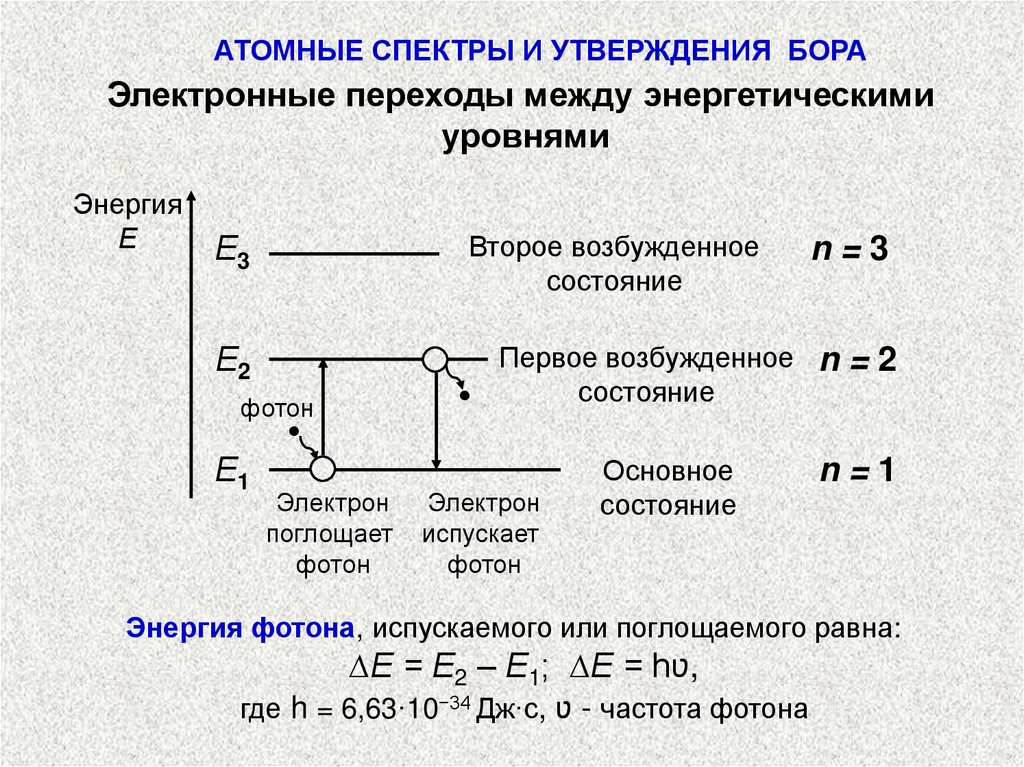
АТОМНЫЕ СПЕКТРЫ И УТВЕРЖДЕНИЯ БОРА
Электронные переходы между энергетическими
уровнями
Энергия
Е
Е3
Второе возбужденное
состояние
Е2
Первое возбужденное n = 2
состояние
фотон
Е1
n=3
Электрон
поглощает
фотон
Электрон
испускает
фотон
Основное
состояние
n=1
Энергия фотона, испускаемого или поглощаемого равна:
∆Е = Е2 – Е1; ∆Е = hʋ,
где h = 6,63·10−34 Дж·с, ʋ - частота фотона

14.

Схема уровней энергии и квантовые переходы
электрона атома водорода
серия Пашена
0
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
-12
-13
-14
n=∞
n=5
n=4
n=3
n=2
серия Бальмера
n=1
серия Лаймана

15.

КВАНТОВАЯ МОДЕЛЬ СТРОЕНИЯ АТОМА
В основе современного учения о строении атома
лежат преставления квантовой механики о том, что
движение и взаимодействие микрообъектов происходит по законам, отличным от законов классической
механики.
ОСНОВОПОЛАГАЮЩИЕ ИДЕИ КВАНТОВОЙ
МЕХАНИКИ
1. Дискретность или квантование энергии.
2. Корпускулярно – волновой дуализм микрочастиц.
3. Вероятностный характер законов микромира.

16.

КВАНТОВАЯ МОДЕЛЬ АТОМА
КВАНТОВАНИЕ ЭНЕРГИИ.
Планк (1900 г.), Эйнштейн (1905 г.)
Е=h·ν
h – постоянная Планка = 6,63 · 10 -34 Дж·с
λ·ν=с
с – скорость света = 3 · 108 м/с

17.

ВОЛНОВОЙ ХАРАКТЕР ДВИЖЕНИЯ МИКРОЧАСТИЦ
Корпускулярно – волновая двойственность.
Свет (и другие электро – магнитные излучения), обладает
как свойствами волны (дифракция, интерференция), так и
свойствами частицы (явление фотоэффекта, уменьшение
массы Солнца на 1,5·1017 кг/год ).
В 1924 г. Луи де Бройль выдвинул гипотезу, что с
каждым движущимся материальным объектом связан
волновой процесс, длина волны которого определя-ется
по формуле:
h
λ =
mV
m – масса частицы; V – скорость частицы; h = 6,63·10-34
Дж·с

18.

КВАНТОВАЯ МОДЕЛЬ АТОМА
КОРПУСКУЛЯРНО – ВОЛНОВАЯ ДВОЙСТВЕННОСТЬ.
Для электрона:
m = 9,1· 10 –31 кг;
V = 1,2 · 108 м/с
6,63 · 10 –34
λ =
= 0,6 · 10 –11 /м/
9,1· 10 –31 ·1,2·108
Для пули:
m = 25 г;
V = 900 м/с
6,63 · 10 –34
λ =
= 2,9 · 10 –35 /м/
25 · 10–3 · 9·102
!!!

19.

ВЕРОЯТНОСТНЫЙ ХАРАКТЕР ЗАКОНОВ МИКРОМИРА.
ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ
(ГЕЙЗЕНБЕРГ, 1927 Г.)
Двойственную природу микрочастиц объясняет
принцип неопределенности:
«невозможно одновременно определить и
скорость (или импульс Р = m·V) и положение
микрочастицы (ее координаты)»:
h
ΔX·ΔV >
2πm
Произведение неопределенностей положения ΔX
и скорости ΔV не может быть меньше чем h / 2πm

20.

ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ (ГЕЙЗЕНБЕРГ, 1927 Г.)
(продолжение)
Например: Неопределенность в положении
электрона, движущегося со скоростью 9 · 106 м/с,
составит:
6,63 · 10 –34
–10 м
∆х =
=
0,6
·
10
2· 3,14 · 9,1 · 10–31 · 9·106
при размере атома порядка 10–10
В то же время неопределенность в положении
автомашины: m = 1 т; V = 100 км/час – составляет:
ΔX =
6,63 · 10–34 · 3600
2 · 3,14 · 103 · 105
= 3,8 · 10 –39 м

21.

КВАНТОВАЯ МОДЕЛЬ АТОМА
УРАВНЕНИЕ ШРЕДИНГЕРА
Квантовая механика описывает движение
электрона в атоме при помощи так называемой
волновой функции ψ. Общий вид этой функции
находится из уравнения Шредингера, которое
связывает волновую функцию ψ с потенциальной
энергией электрона (U) и его полной энергией (Е)
d2 ψ
d2 ψ
+
+
2
2
dx
dy
d2 ψ
8 π2 m
+
(E – U)ψ = 0
2
2
dz
h

22.

ВОЛНОВАЯ ФУНКЦИЯ
Волновая функция ψ, являющаяся решением
уравнения Шредингера, называется атомной
орбиталью (АО).
Физический смысл ψ – функции состоит в
следующем:
квадрат
волновой
функции
(ψ2)
определяет плотность вероятности нахождения
электрона в некоторой точке с координатами (x; y; z).
Это означает, что вероятность нахождения
частицы (электрона) в небольшом элементе
объема dV вокруг точки (x; y; z) определяется
произведением:
ψ2·dV

23.

ВЕРОЯТНОСТЬ НАХОЖДЕНИЯ ЭЛЕКТРОНА
В АТОМЕ НА РАССТОЯНИИ R ОТ ЯДРА
4π r2 ψ2
ЭЛЕКТРОННОЕ
ОБЛАКО
0,53 A0
r

24.

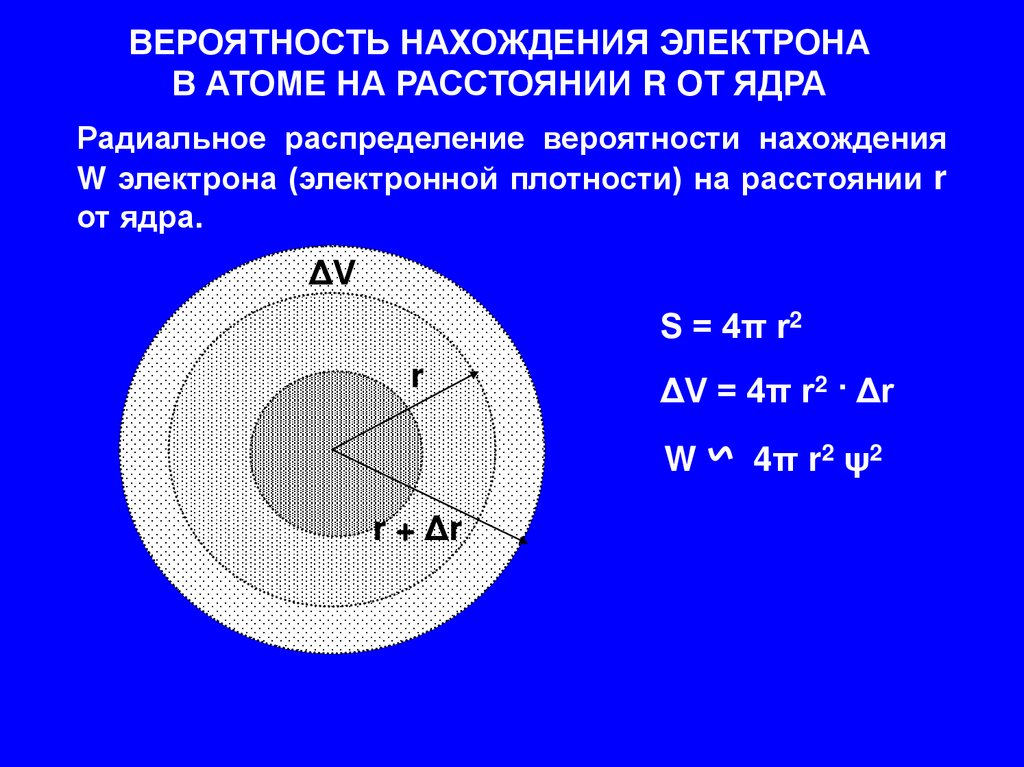
ВЕРОЯТНОСТЬ НАХОЖДЕНИЯ ЭЛЕКТРОНА
В АТОМЕ НА РАССТОЯНИИ R ОТ ЯДРА
Радиальное распределение вероятности нахождения
W электрона (электронной плотности) на расстоянии r
от ядра.
ΔV
S = 4π r2
r
ΔV = 4π r2 · Δr
W
r + Δr
4π r2 ψ2

25.

ВОЛНОВАЯ ФУНКЦИЯ
(продолжение)
Определяя значение ψ – функции, удовлетворяющей
уравнению Шредингера, мы находим то околоядерное
пространство, в котором с наибольшей вероятностью
пребывает электрон.
Околоядерное пространство, в котором с
наибольшей вероятностью пребывает
электрон есть атомная орбиталь.
Из уравнения Шредингера следует, что атомную
орбиталь
можно
однозначно
описать
тремя
параметрами:
Ψ = Ψ (n, l, m)
эти параметры получили название квантовых чисел.

26.

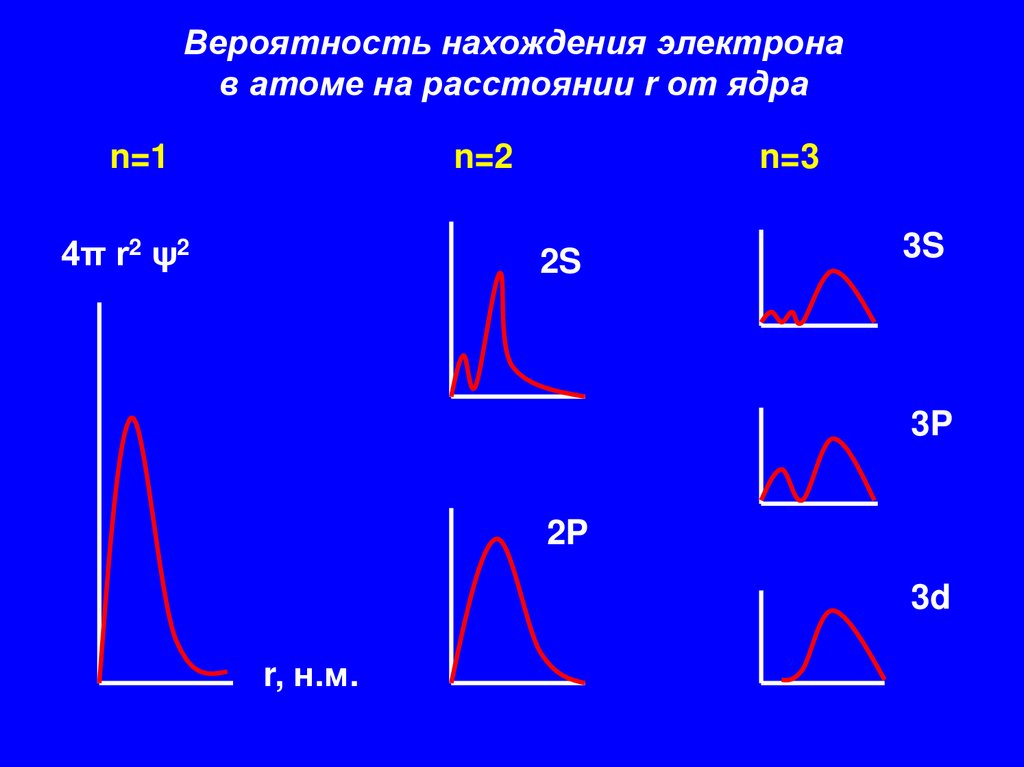
Вероятность нахождения электрона
в атоме на расстоянии r от ядра
n=1
n=2
4π r2 ψ2
n=3
2S
3S
3P
2P
3d
r, н.м.