Similar presentations:
Иррациональные уравнения
1. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
2. эпиграф
И чем труднеедоказательство, тем больше
будет удовольствия тому,
кто доказательство найдет.
Рене Декарт
3.
Иррациональное(от лат. irrationalis неразумный,
бессознательный)
находящееся за пределами разума,
противоречащее логике.
Обычно противопоставляется
рациональному как разумному,
целесообразному, обоснованному.
4.
ПОНЯТИЕ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯЕсли в уравнении переменная содержится
под знаком квадратного корня, то
уравнение называют иррациональным.
f ( x) g ( x)
5.
Примеры:2x 1 3
2x 5 4x 7
2 x 5x 2 x 6
2
6.
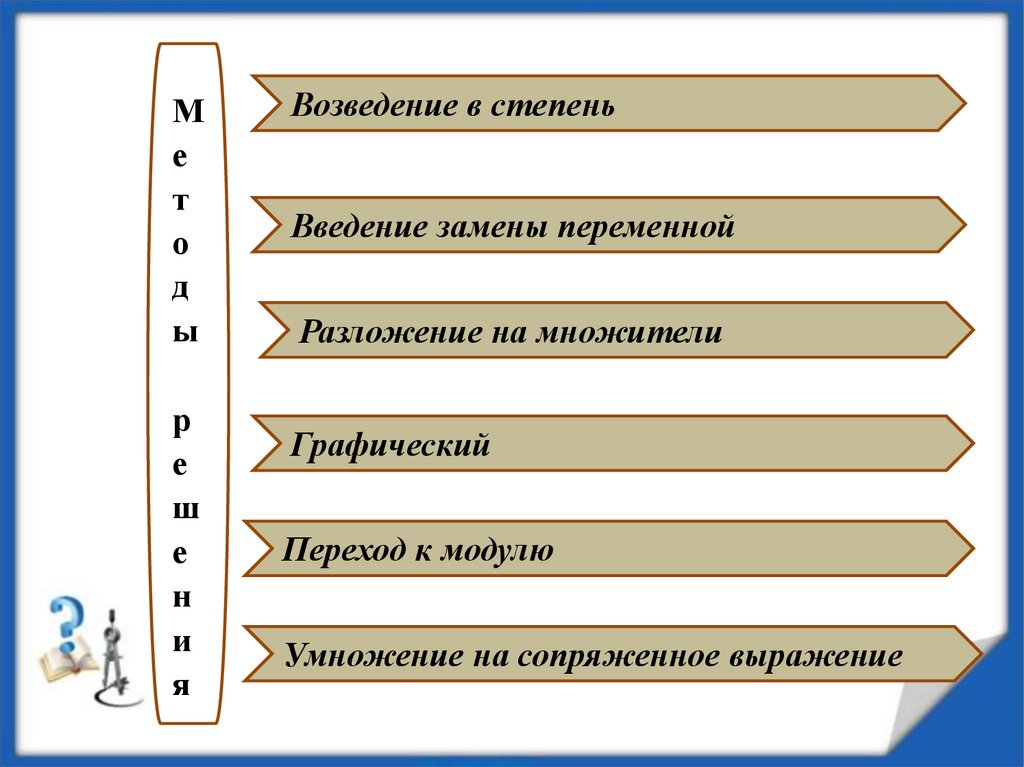
Ме
т
о
д
ы
р
е
ш
е
н
и
я
Возведение в степень
Введение замены переменной
Разложение на множители
Графический
Переход к модулю
Умножение на сопряженное выражение
7.
ИЗУЧАЕМ НОВОЕМетод возведения в квадрат обеих частей
уравнения
2x 1 3
2x 1 3
2
2x 1 9
2x 8
x 4
Ответ: x 4
8.
ПРОВЕРКА2 * 4 1 3
9 3
3 = 3 (верно)
9.
ИЗУЧАЕМ НОВОЕМетод возведения в квадрат обеих частей
уравнения
2x 5 4x 7
( 2x 5) ( 4x 7 )
2
2x 5 4x 7
x 1
Проверим!!!
2
10.
ПРОВЕРКАПодставим 1 вместо х в заданное
иррациональное уравнение, получим:
2 1 5 4 1 7
3 3
x 1 - посторонний корень
Ответ: иррациональное уравнение не
имеет корней
11.
ЗАПОМНИ1) Возвести обе части уравнения
в квадрат.
2) Обязательно сделать
проверку!!!
12.
ИЗУЧАЕМ НОВОЕМетод замены переменной
х 5 х 6 0
Делаем замену :
х t
x t2
t 2 5t 6 0
D 25 24 49
t1 6, t 2 1
Заменяем :
х 6
- посторонний корень
х 1, х 1
Ответ : х 1











 mathematics
mathematics








