Similar presentations:
Параллельные прямые, перпендикулярные к плоскости
1.
2.
D1C1
A1
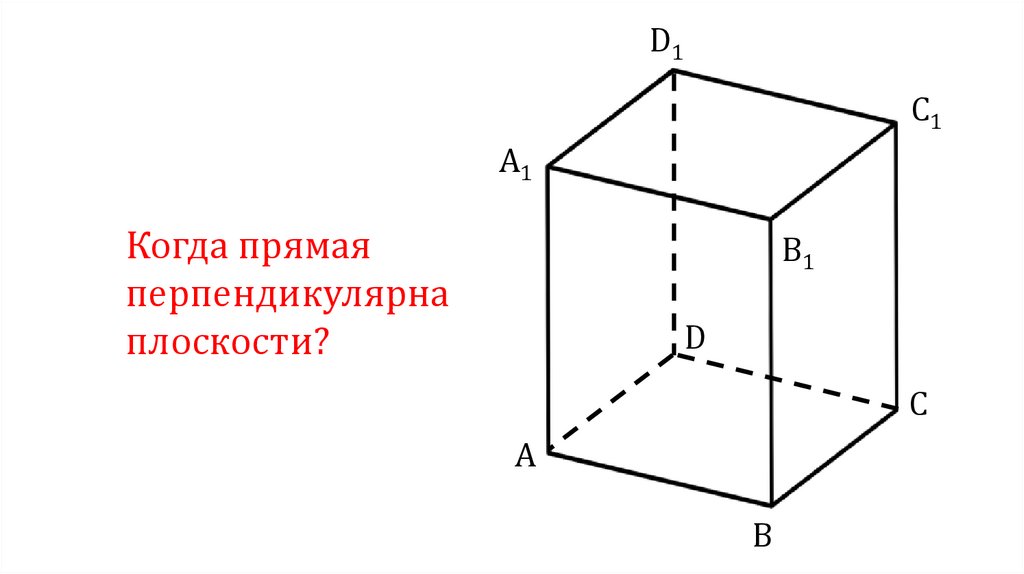
Когда прямая
перпендикулярна
плоскости?
B1
D
C
A
B
3.
D1C1
A1
B1
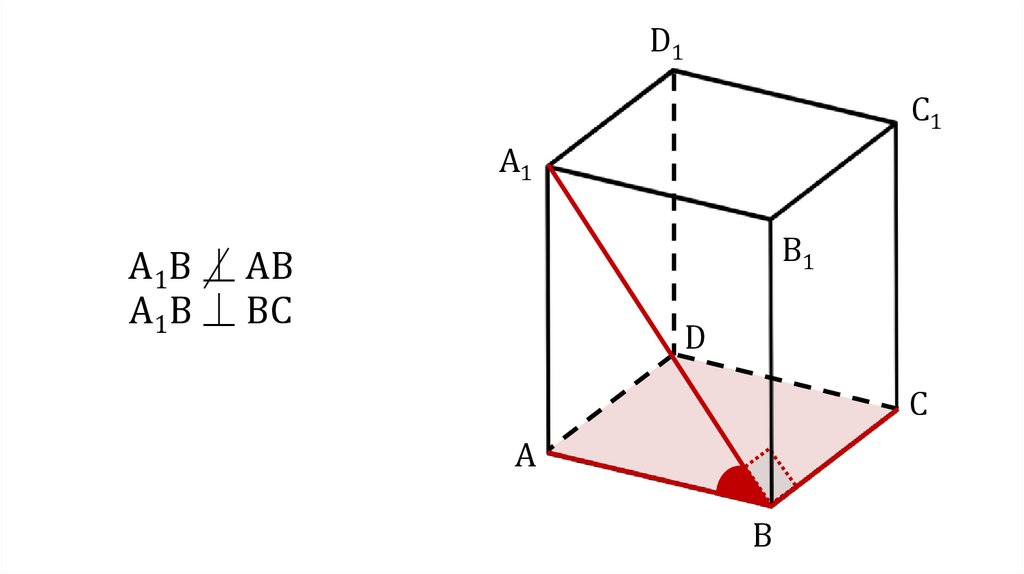
А1В ⏊ АВ
А1В ⏊ ВС
D
C
A
B
4.
D1C1
A1
B1
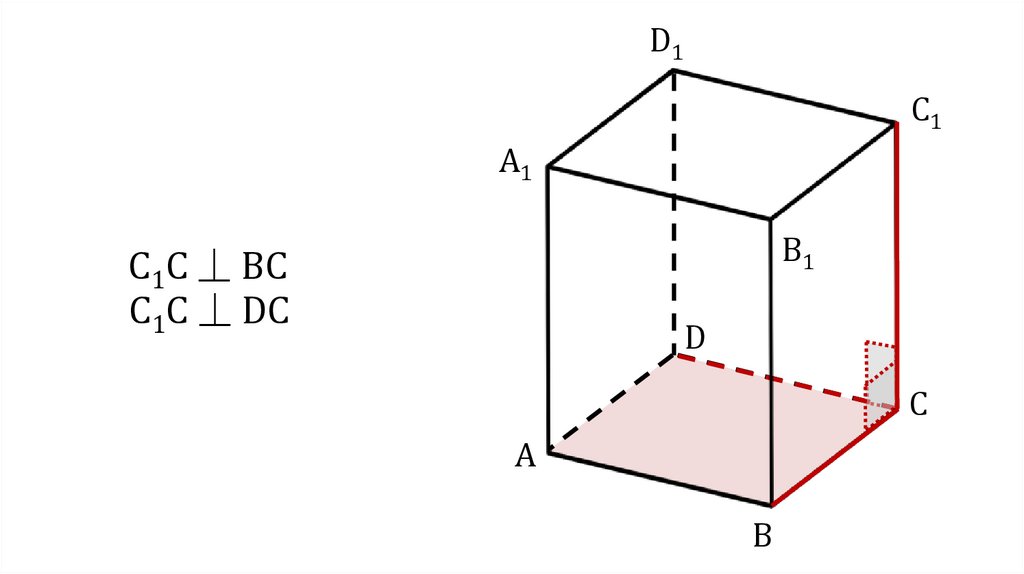
C1C ⏊ ВC
C1C ⏊ DС
D
C
A
B
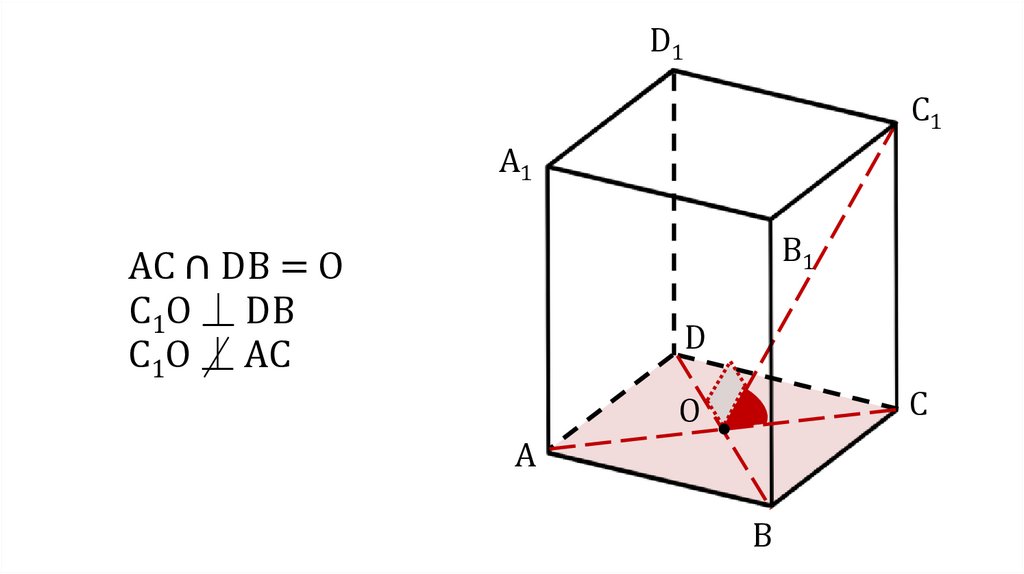
5.
D1C1
A1
B1
AC ∩ DВ = O
C1O ⏊ DB
C1O ⏊ AC
D
C
O
A
B
6.
D1D1
D1
C1
A1
C1
A1
C1
A1
B1
B1
B1
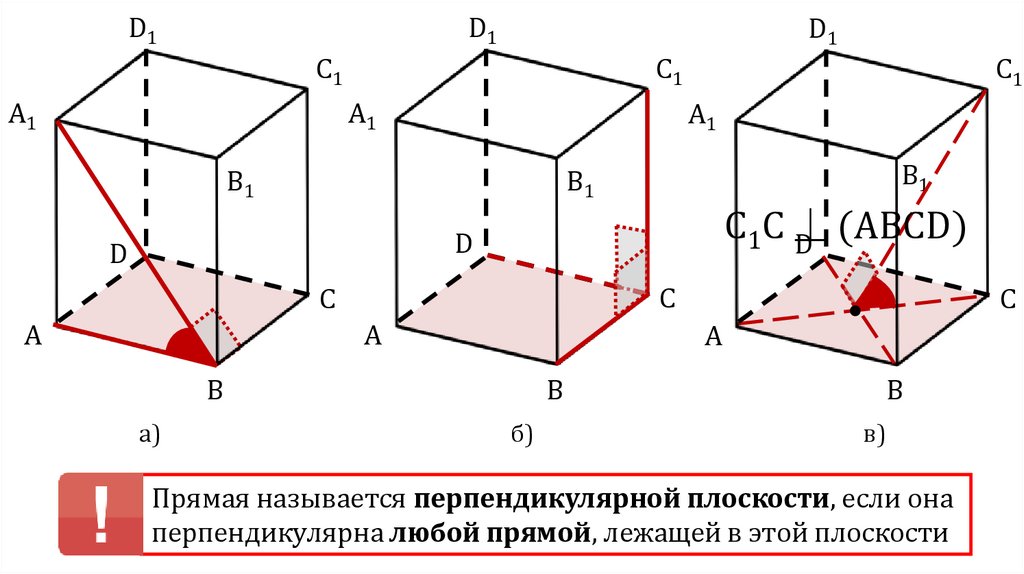
С1С ⏊
(АВСD)
D
D
D
C
C
A
A
A
B
B
а)
C
б)
B
в)
Прямая называется перпендикулярной плоскости, если она
перпендикулярна любой прямой, лежащей в этой плоскости
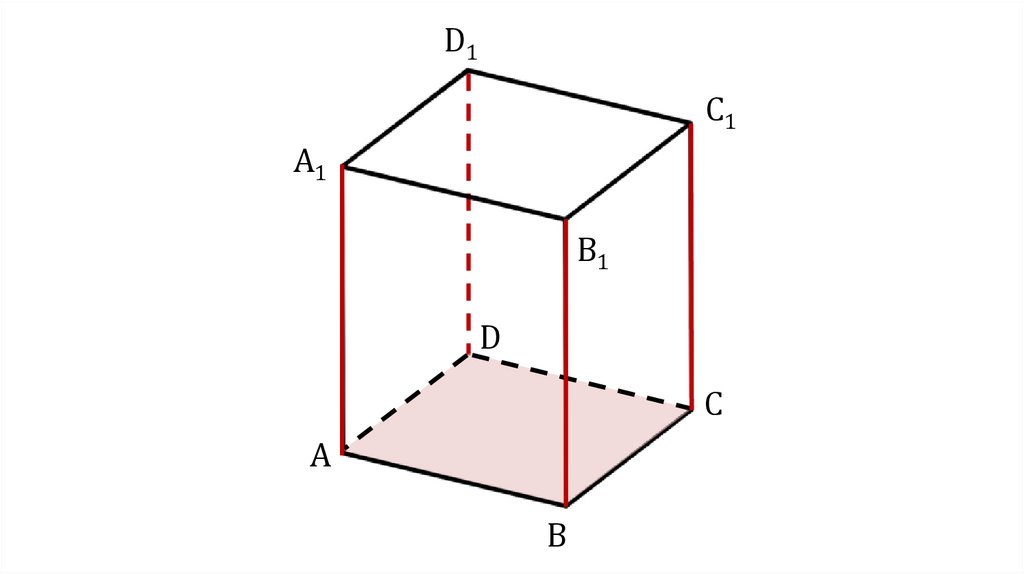
7.
D1C1
A1
B1
D
C
A
B
8.
ТеоремаЕсли одна из двух параллельных
прямых перпендикулярна
плоскости, то и другая прямая
перпендикулярна этой плоскости
9.
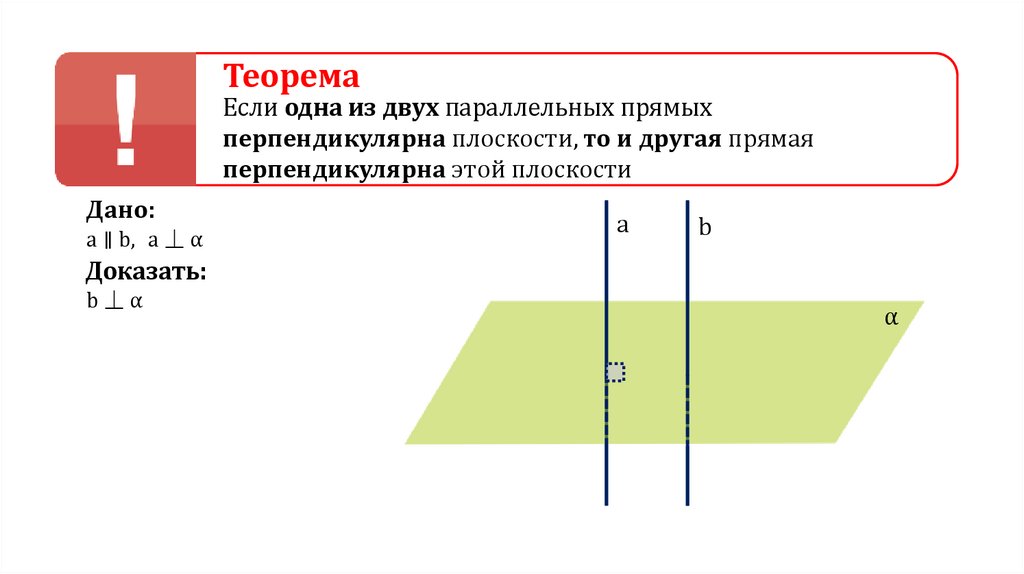
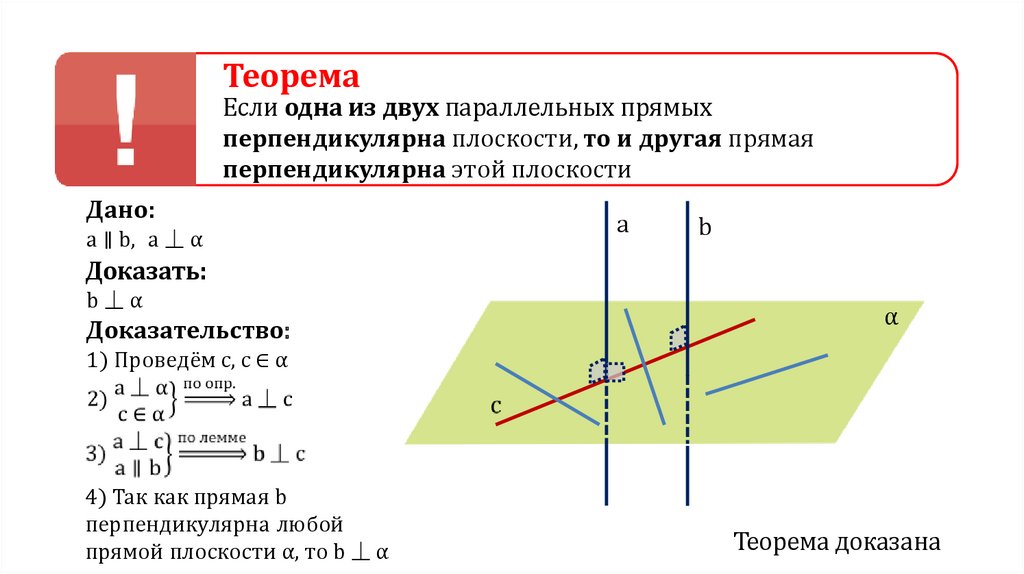
ТеоремаЕсли одна из двух параллельных прямых
перпендикулярна плоскости, то и другая прямая
перпендикулярна этой плоскости
Дано:
a ∥ b, a ⏊ α
a
b
Доказать:
b⏊α
α
10.
ТеоремаЕсли одна из двух параллельных прямых
перпендикулярна плоскости, то и другая прямая
перпендикулярна этой плоскости
Дано:
a ∥ b, a ⏊ α
a
b
Доказать:
b⏊α
Доказательство:
α
1) Проведём с, с ∈ α
4) Так как прямая b
перпендикулярна любой
прямой плоскости α, то b ⏊ α
Теорема доказана
11.
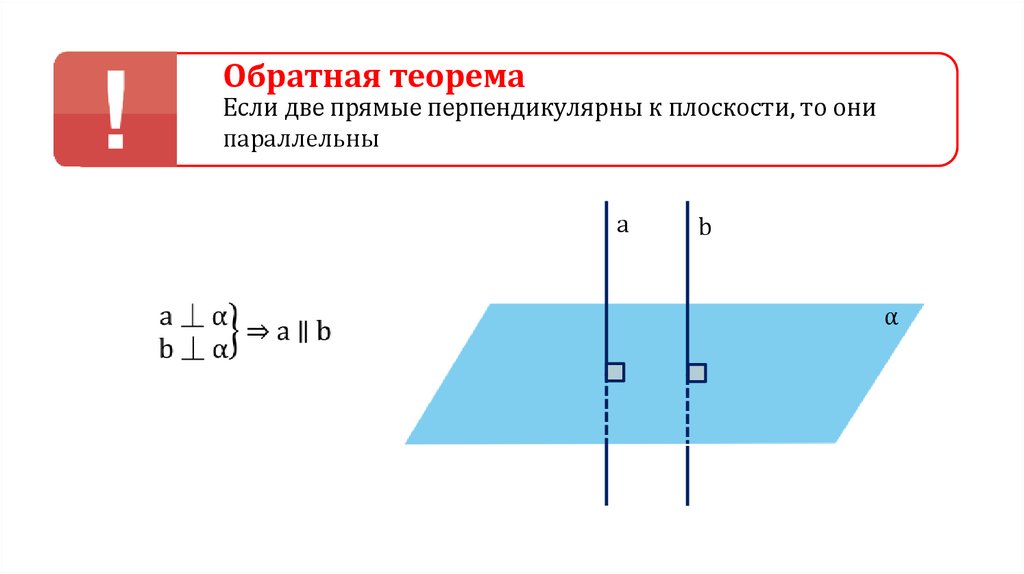
Обратная теоремаЕсли две прямые перпендикулярны к плоскости, то они
параллельны
a
b
α
12.
Задача 1B1
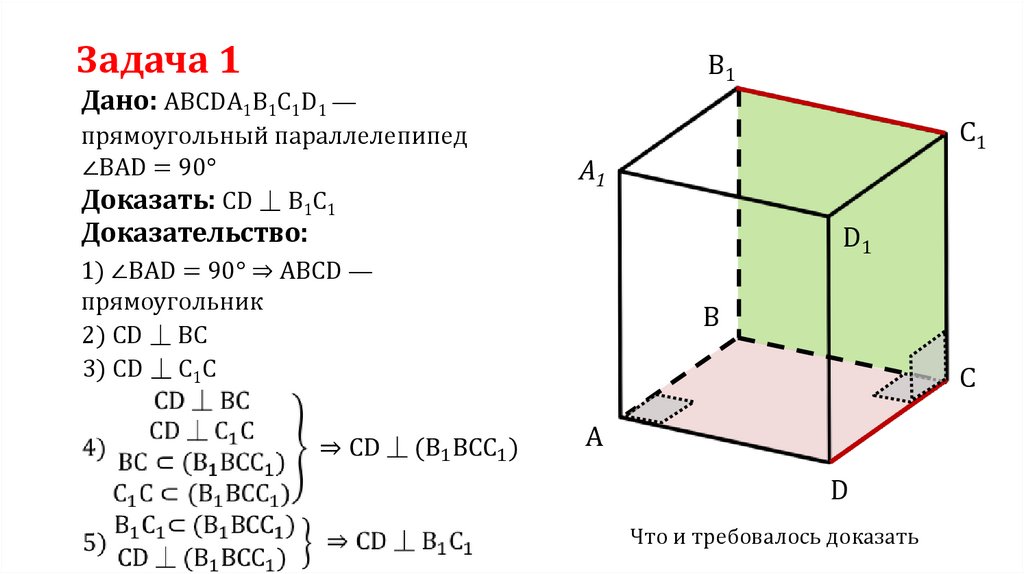
Дано: АВСDА1В1С1D1 —
прямоугольный параллелепипед
∠ВАD = 90°
Доказать: CD ⏊ В1С1
C1
A1
Доказательство:
D1
1) ∠ВАD = 90° ⇒ АВСD —
прямоугольник
2) CD ⏊ BС
3) CD ⏊ С1С
B
C
A
D
Что и требовалось доказать
13.
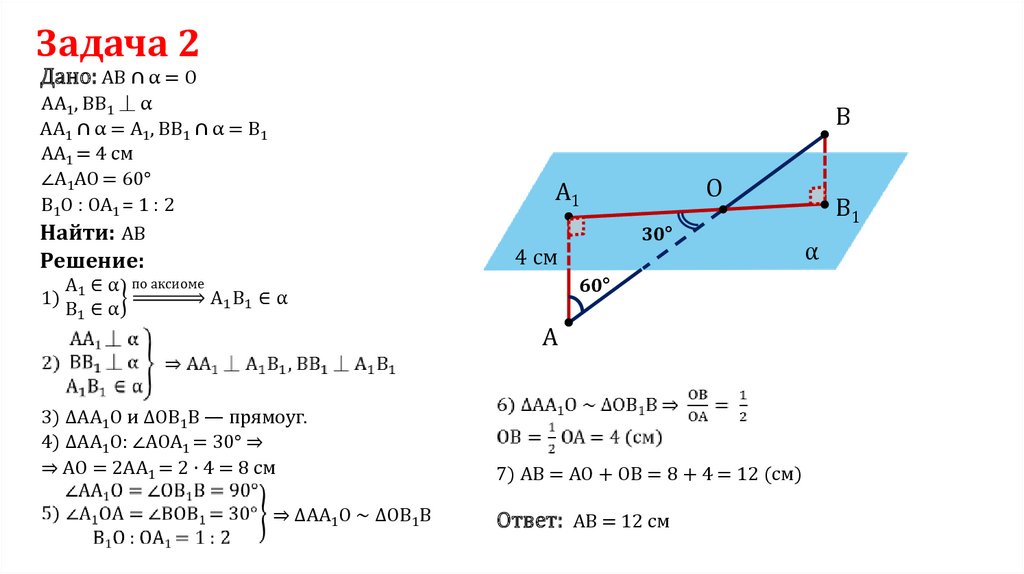
Задача 2Дано: АВ ∩ α = O
AA1, BB1 ⏊ α
AA1 ∩ α = А1, BB1 ∩ α = B1
AA1 = 4 см
∠A1AO = 60°
B1O : OA1 = 1 : 2
Найти: AВ
B
O
A1
30°
4 см
Решение:
60°
A
3) ΔАА1О и ΔОВ1В — прямоуг.
4) ΔАА1О: ∠АОА1 = 30° ⇒
⇒ АО = 2АА1 = 2 · 4 = 8 см
⇒ ΔАА1О ∼ ΔОВ1В
7) АВ = AO + OB = 8 + 4 = 12 (см)
Ответ: AB = 12 см
B1
α


 mathematics
mathematics