Перпендикулярности прямой и плоскости

1.

2.

3.

ЦЕЛЬ УРОКА:

4.

5.

Учебные достижения по изучению темы
- знать определение перпендикулярных прямой
и плоскости, их свойства, признак
перпендикулярности прямой и плоскости;
- уметь применять их при решении задач;
- уметь доказывать признак
перпендикулярности прямой и плоскости

6.

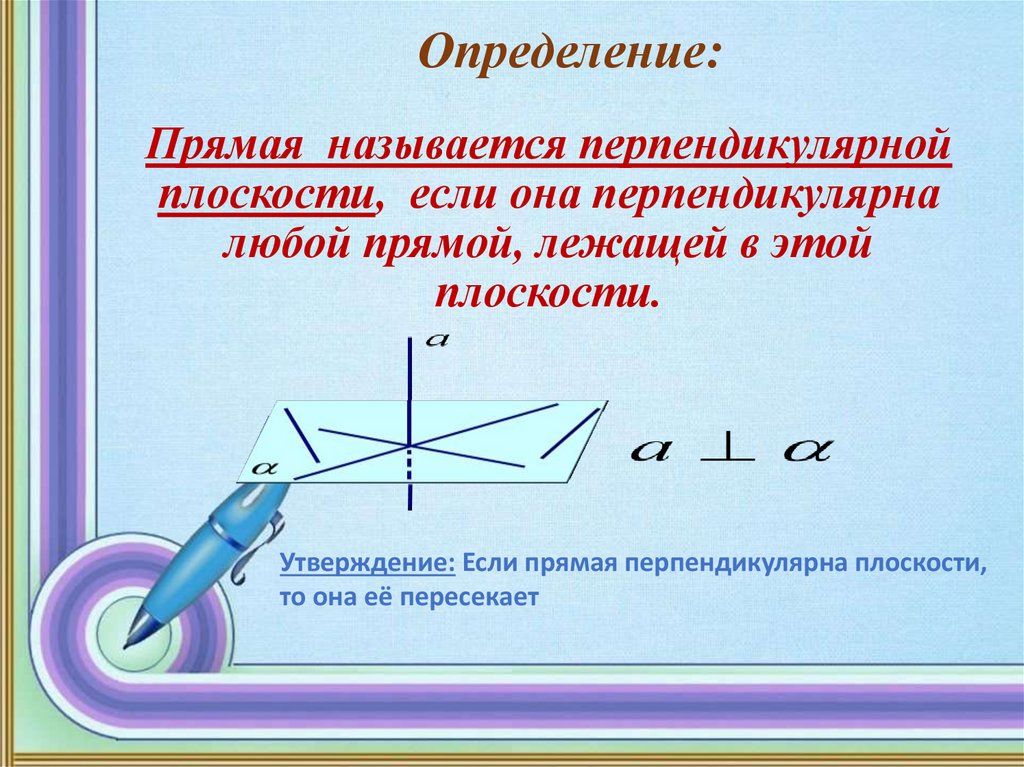
Определение:
Прямая называется перпендикулярной
плоскости, если она перпендикулярна
любой прямой, лежащей в этой
плоскости.
Утверждение: Если прямая перпендикулярна плоскости,
то она её пересекает

7.

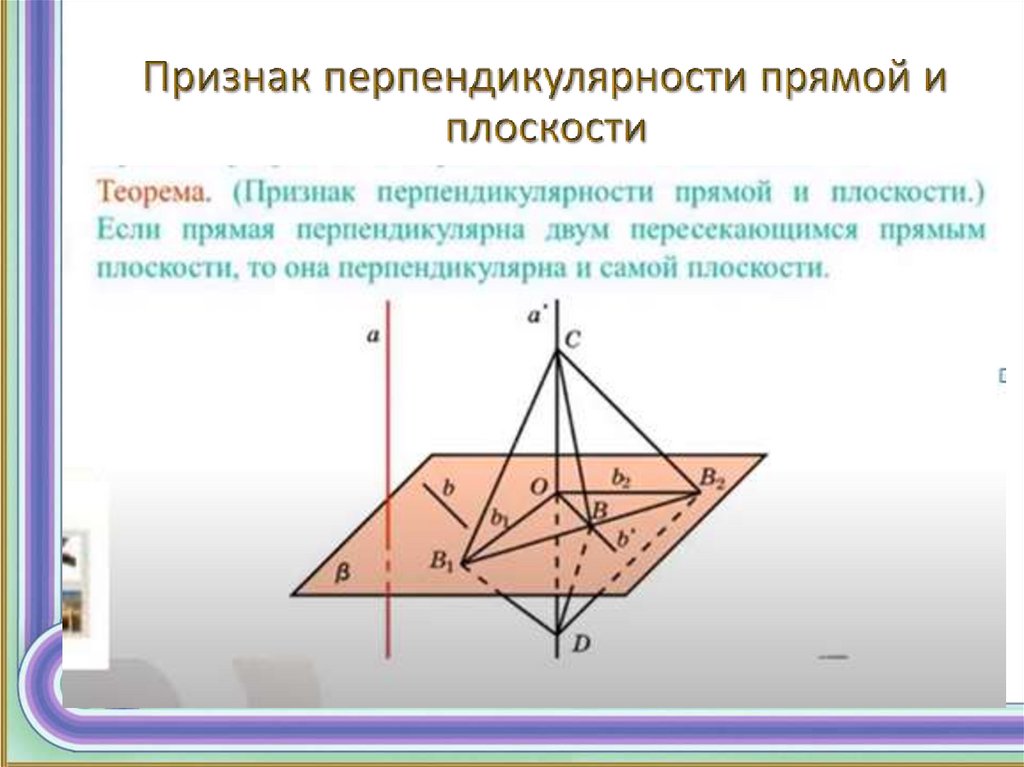
Теорема 1. Если одна из двух параллельных прямых
перпендикулярна плоскости, то и другая прямая,
перпендикулярна этой плоскости.
Теорема 2. Если две прямые перпендикулярны
плоскости, то они параллельны.
Теорема: через любую точку пространства
проходит прямая, перпендикулярная к данной
плоскости, и притом только одна.

8.

9.

Критерии оценивания:
- знают определение перпендикулярности
прямой и плоскости.
- знают свойство перпендикулярности прямой
и плоскости.
- применяют признак перпендикулярности
прямой и плоскости при решении задач.

10.

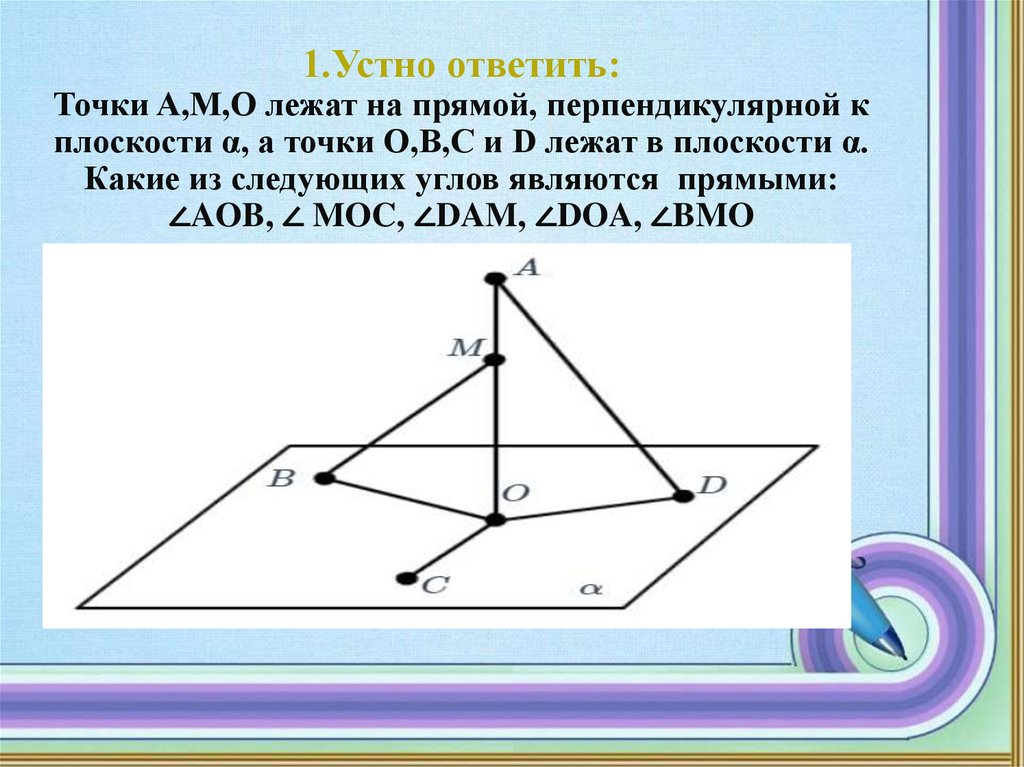
1.Устно ответить:
Точки A,M,O лежат на прямой, перпендикулярной к
плоскости α, а точки O,B,C и D лежат в плоскости α.
Какие из следующих углов являются прямыми:
∠AOB, ∠ MOC, ∠DAM, ∠DOA, ∠BMO

11.

12.

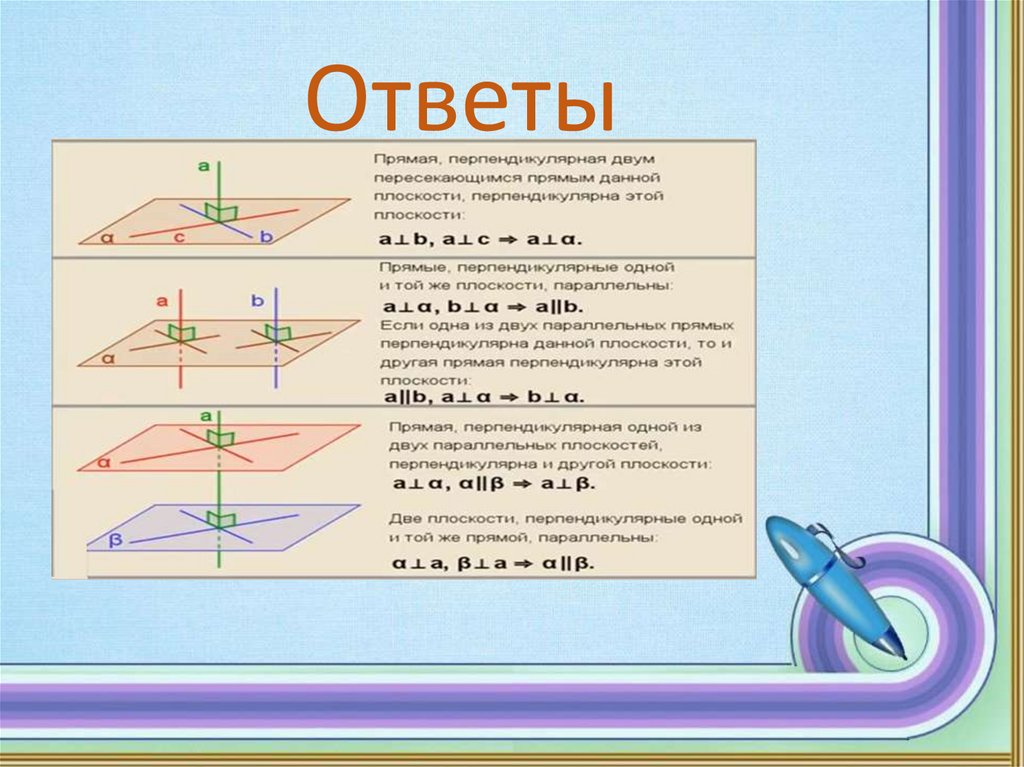
Ответы

13.

14.

15.

16.

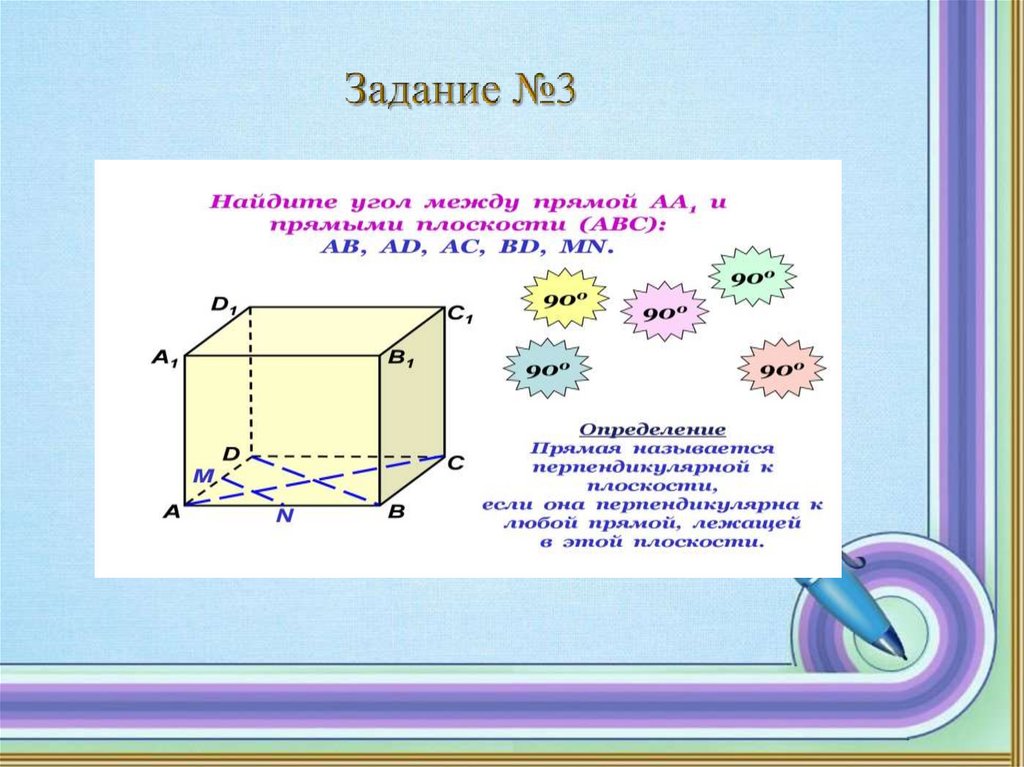
6.Задания для формативного оценивания

17.

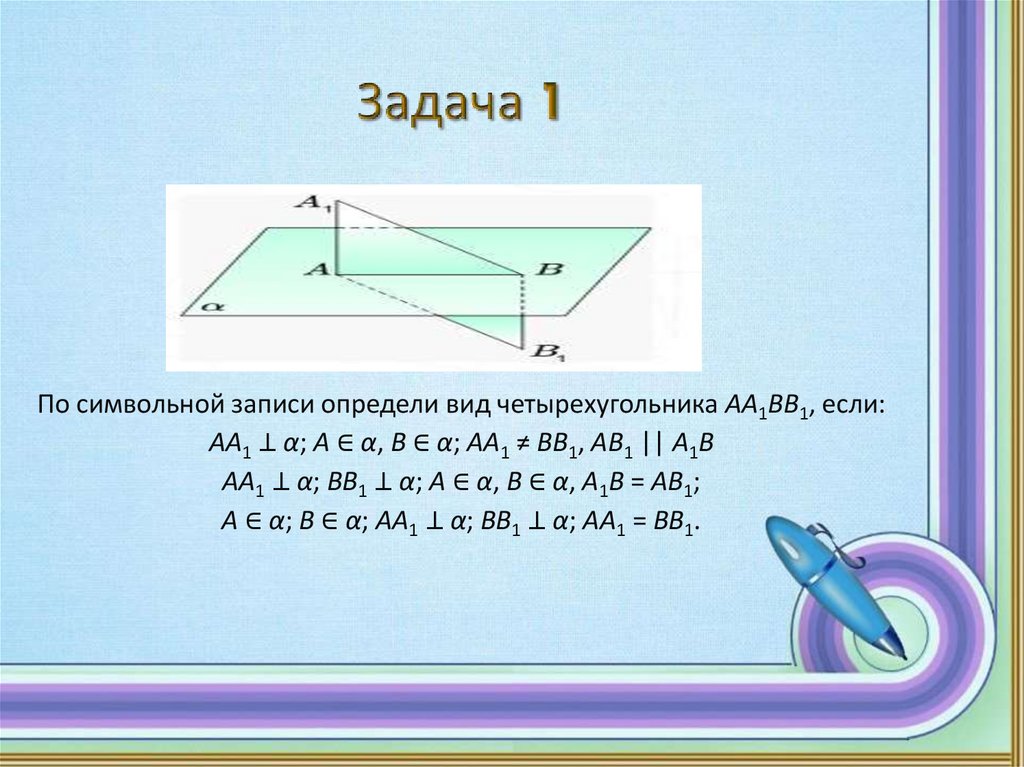
По символьной записи определи вид четырехугольника AA1BB1, если:
AA1 ⊥ α; A ∈ α, B ∈ α; AA1 ≠ BB1, AB1 || A1B
AA1 ⊥ α; BB1 ⊥ α; A ∈ α, B ∈ α, A1B = AB1;
A ∈ α; B ∈ α; AA1 ⊥ α; BB1 ⊥ α; AA1 = BB1.

18.

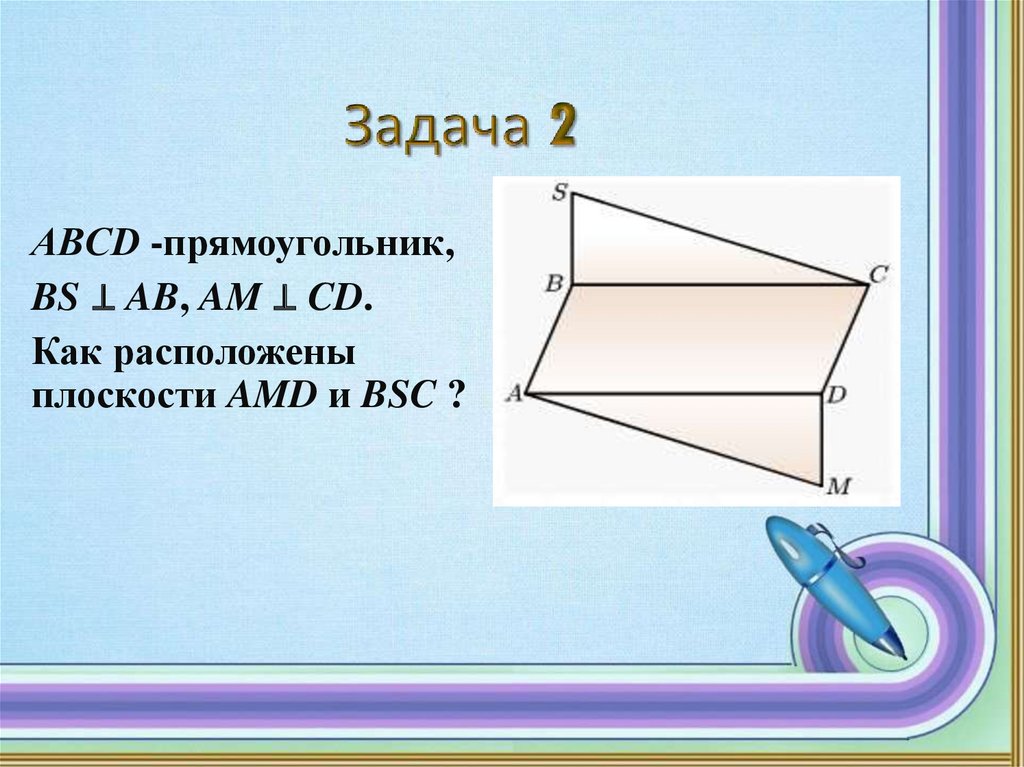
АBCD -прямоугольник,
BS ⊥ AB, AM ⊥ CD.
Как расположены
плоскости AMD и BSC ?

19.

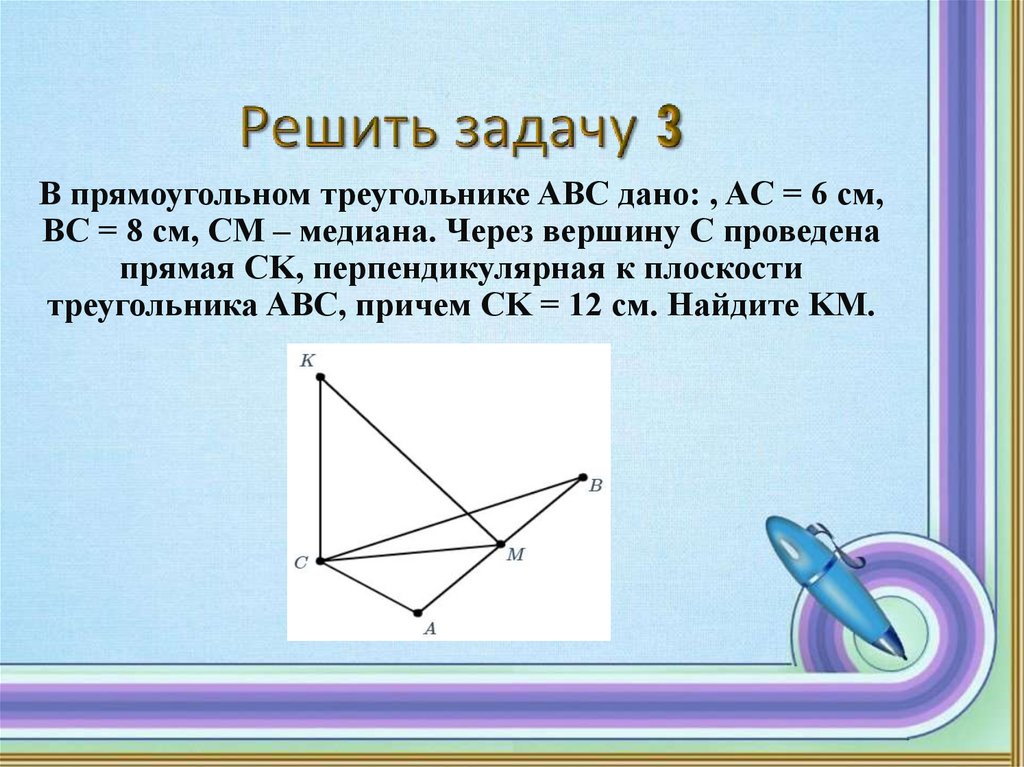
В прямоугольном треугольнике ABC дано: , AC = 6 см,
BC = 8 см, CM – медиана. Через вершину C проведена
прямая CK, перпендикулярная к плоскости
треугольника ABC, причем CK = 12 см. Найдите KM.

20.

ЗАДАЧА 4

21.

Дано: ΔACB-равностронний .