Урок 15. Точечная оценка числовой характеристики случайной величины, ее свойства

1. Урок 15. Точечная оценка числовой характеристики случайной величины, ее свойства.

2. Определение.

Выборочная оценка, используемая в качестве приближенного
значения неизвестной генеральной характеристики, называется
ее точечной статистической оценкой.
Генеральная совокупность, Г
Генеральная характеристика,
Выборка, Vn
Точечная оценка,
Математическое ожидание, МХ
Х
2
Выборочная дисперсия, S
Выборочная средняя,
Генеральная дисперсия, DX
Среднеквадратическое
отклонение, х
Выборочное отклонение,
S
Вероятность, Р
Относительная частота,

3.

1.
Вопрос: Как хорошо выбрано приближение?
Свойства точечных оценок:
Точечная оценка называется состоятельной,
если для любого значения 0 выполняется условие
lim P( ) 1
n
Чем больше объем информации, тем оценка
более состоятельна, Vn>30% от генеральной
совокупности (Г).

4. 2. Оценка называется несмещенной, если для любого фиксированного числа наблюдений n выполняется условие:

М ( n )
т.е. среднее значение оценки совпадает с
точным значением генеральной
характеристики.

5. 3. Несмещенная оценка генеральной характеристики называется эффективной, если она среди всех несмещенных оценок той же характеристики обл

3. Несмещенная оценка
генеральной
характеристики называется эффективной, если она
среди всех несмещенных оценок той же
характеристики обладает наименьшей дисперсией.
Закон
распределения
Нормальный
закон
распределения
Х
1
0
Р
р
1-р
min X
2
n
-
min DX
4
n
р (1 р )
n

6. Задача.

1.
2.
3.
4.
Пусть генеральную совокупность образуют 5
чисел: -2;-1;0;2;6.
Вычислить генеральное среднее и
генеральную дисперсию;
Составить все возможные выборки с
возвратом объема n=2;
Для каждой выборки определить
выборочную среднюю и выборочную
дисперсию;
Установить, какими свойствами обладают
выборочные характеристики.

7. Решение:

1.
Составить ряд распределения и вычислить
генеральные характеристики:
Х
-2
-1
0
2
6
Р
1/5
1/5
1/5
1/5
1/5
МХ=1/5(-2-1+0+2+6)=1
ДХ=1/5((-2-1)2+(-1-1)2+(0-1)2+(2-1)2+(6-1)2)=8

8.

2. Составить все возможные выборки с возвратом объема
n=2 и вычислить для каждой выборочную среднюю и
выборочную дисперсию, заполнив таблицу:
Выборка
Х1 Х2
Р(х1;х2)
х х
Х 1 2
2
-2 -2
1/25
-2
Х
4
2
2
2
2
х
х
2
Х 2 1 2 DX X (X )
2
4
0

9.

3. Построить ряд распределения выборочной средней и найти ее
математическое ожидание:4.
-2
-3/2
-1
-1/2
0
1/2
1
2
5/2
3
4
6
Х
Р
1/25 2/25 3/25 2/25 3/25 2/25 2/25 3/25 2/25 2/25 2/25 1/25
МХ
1
3
1
1
5
( 2 1 2 1 3 2 0 3 2 1 2 2 3 2 3 2 4 2 6 1) 1
25
2
2
2
2
Аналогично, построить ряд распределения выборочных дисперсий и
найти их математическое ожидание.

10.

5.
Определить, какими свойствами обладают
выборочные характеристики.
Состоятельность: V(Г)=5; Vn=2 (2/5)*100%=40%>30%,
следовательно оценки состоятельны.
Несмещенность: М ( Х ) МХ 1
М ( DX ) DX
Выборочная средняя несмещенная.
Выборочная дисперсия смещенная.

11.

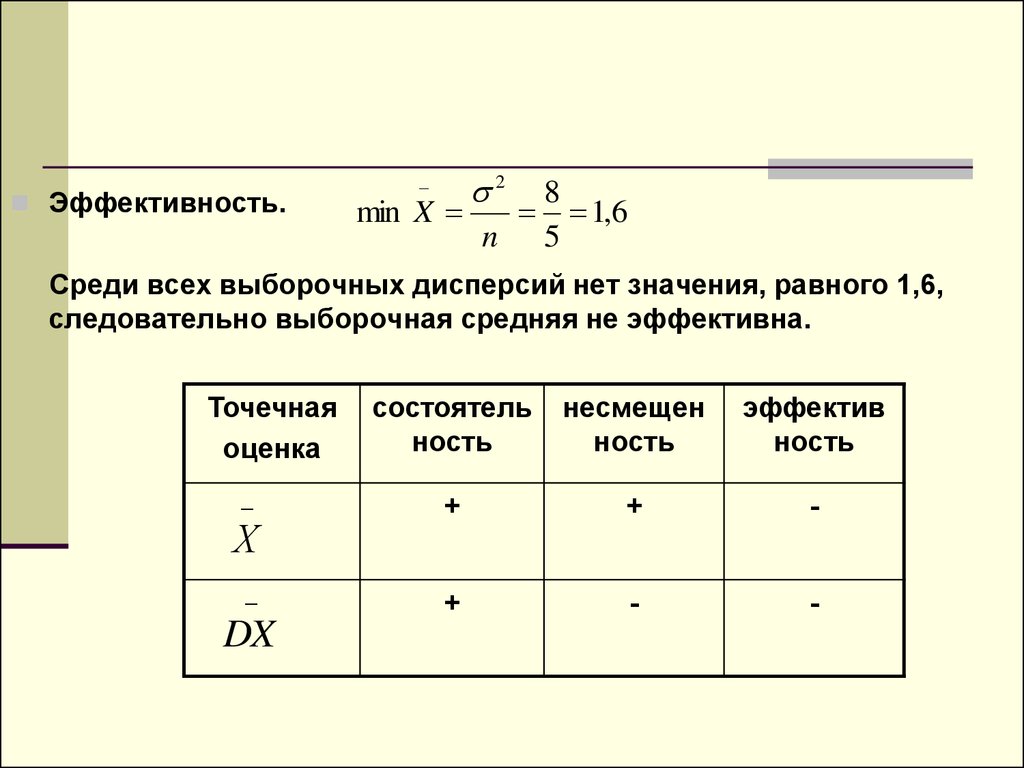
Эффективность.
min X
2
n
8
1,6
5
Среди всех выборочных дисперсий нет значения, равного 1,6,
следовательно выборочная средняя не эффективна.
Точечная
оценка
состоятель
ность
несмещен
ность
эффектив
ность
+
+
-
+
-
-
Х
DX