Постановка задачи оптимизации

1.

1

2.

По виду решаемой задачи – задача оптимизации:
минимизация, максимизация
По размерности решаемой задачи – задача оптимизации:
одномерная, двумерная, …, многомерная
По количеству оптимумов – задача оптимизации:
одноэкстремальная, многоэкстремальная
По количеству критериев – задача оптимизации:
однокритериальная, многокритериальная
По наличию ограничений на значения независимых переменных –
задача оптимизации:
безусловная, условная (обусловленная)
По принципу приближения к оптимуму – методы поиска оптимума:
детерминированные, градиентные, случайные (стохастические)
2

3.

Методы детерминированного поиска позволяют уточнять
решение задачи оптимизации на основе чёткого набора
инструкций, правил
Методы градиентного поиска позволяют уточнять решение задачи
оптимизации на основе информации об изменении (скорости
изменения) значения целевой функции в одной или нескольких
точках
Методы случайного поиска позволяют получать решение задачи
оптимизации на основе выбора случайного направления
движения к точке оптимума
3

4.

Цель решения задачи оптимизации – нахождение условий (значений независимых переменных),
обеспечивающих наилучшее (наименьшее или наибольшее) значение целевой функции (критерия
оптимальности)
Целевая функция, критерий оптимальности – выражение, с помощью которого можно численно
оценить качество возможного решения задачи оптимизации или сравнить несколько возможных
решений между собой
Задача минимизации – требуется найти значения независимых переменных, обеспечивающие
наименьшее значение критерия
Задача максимизации – требуется найти значения независимых переменных, обеспечивающие
наибольшее значение критерия
Можно от задачи минимизации перейти к задаче максимизации и наоборот, поменяв знак
выражения критерия оптимальности на противоположный
Глобальное решение задачи оптимизации – значения независимых переменных, обеспечивающие
наилучшее значение критерия среди всех возможных при заданных в задаче ограничениях
Локальное решение задачи оптимизации – значения независимых переменных, обеспечивающие
лучшее среди всех возможных значение критерия в некоторой локальной области изменения этих
независимых переменных

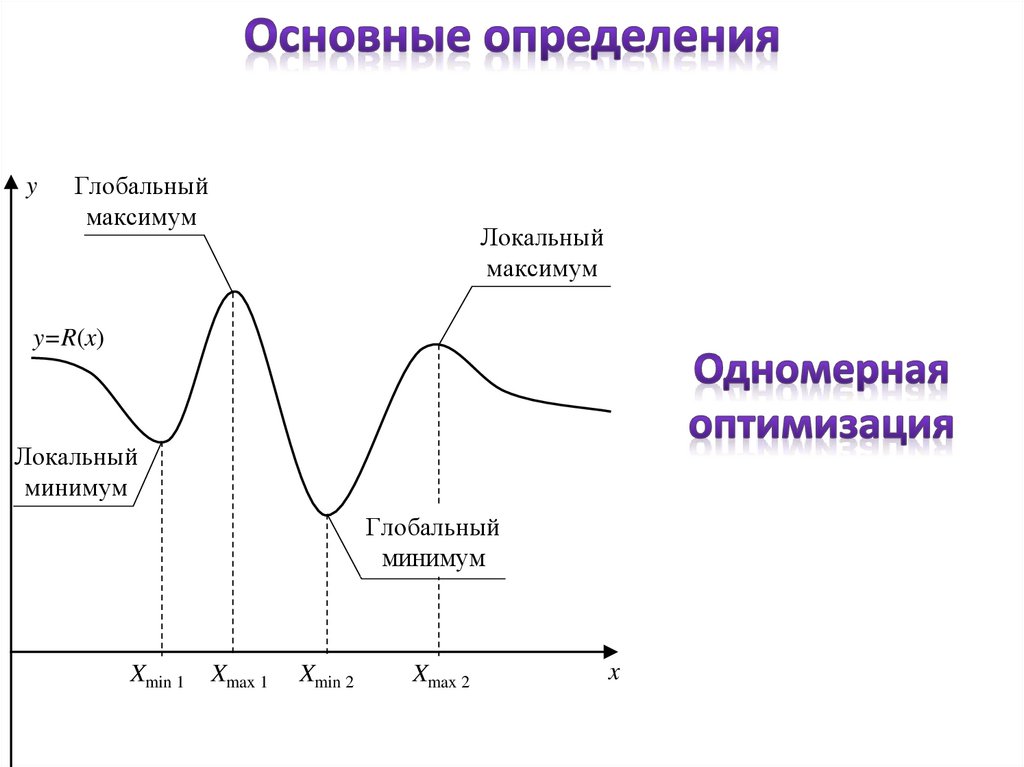
5.

y
Глобальный
максимум
Локальный
максимум
y=R(x)
Локальный
минимум
Глобальный
минимум
Xmin 1
Xmax 1
Xmin 2
Xmax 2
x

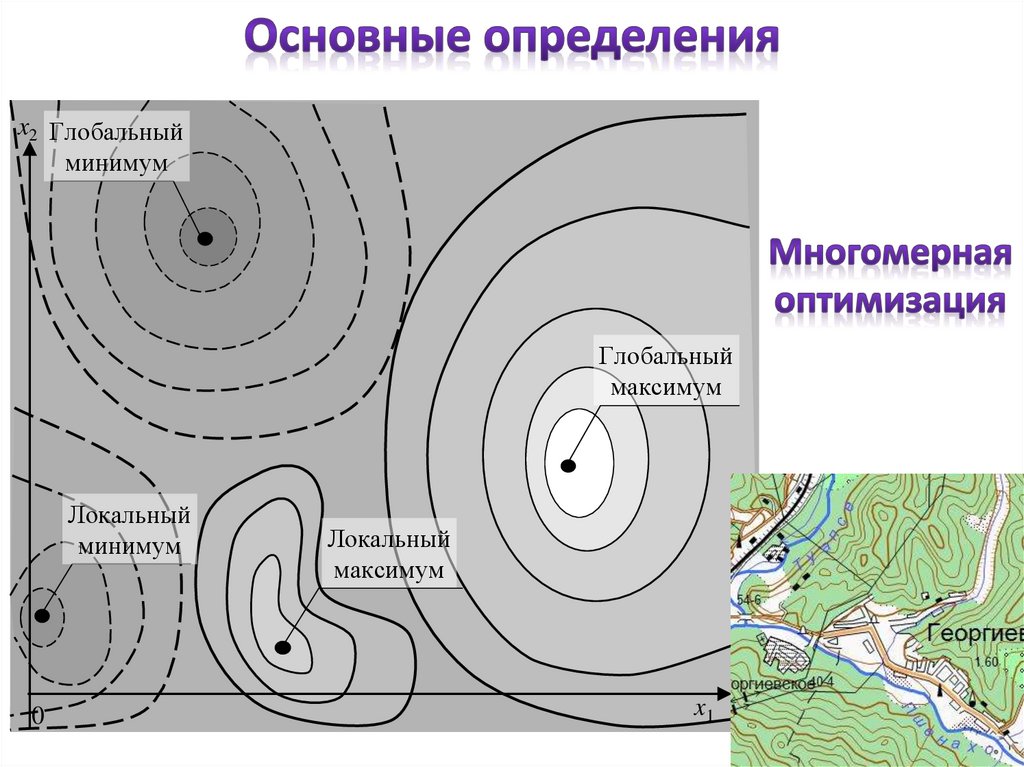
6.

x2 Глобальный
y=R(x1, x2)
минимум
Глобальный
максимум
Локальный
минимум
0
Локальный
максимум
x1

7.

Необходимое условие: точка оптимума должна быть критической
– производная критерия оптимальности равна нулю в точке
оптимума. Но не каждая критическая точка является точкой
оптимума
Достаточное условие: значение критерия оптимальности в точке
оптимума является лучшим среди значений критерия в любой
точке её окрестности – производная критерия меняет знак в точке
оптимума
Методы одномерной оптимизации – методы
детерминированного (локализации экстремума, золотого сечения,
чисел Фибоначчи, парабол) и градиентного (приращений) поиска
7

8.

R R x
dR
0
dx
R R
0
x 2 x
R x x R x x
0
2 x
x
Задача оптимизации сводится к решению
уравнения любым численным методом:
– половинного деления;
– пропорциональных частей;
– Ньютона;
– простых итераций.
R x x R x x 0 – решаемое уравнение
Условие: разный знак функции, стоящей в
левой части уравнения, на границах
начального интервала локализации оптимума
8

9.

R x 6 x
2
x 0, 10
0,01
x
6 x x 6 x x
2
a
0,000
5,000
5,000
5,000
5,625
5,938
5,938
5,938
5,977
5,996
2
d
5,000
7,500
6,250
5,625
5,938
6,094
6,016
5,977
5,996
6,006
b
10,000
10,000
7,500
6,250
6,250
6,250
6,094
6,016
6,016
6,016
0
f(a)
-0,240
-0,040
-0,040
-0,040
-0,015
-0,003
-0,003
-0,003
-0,001
0,000
f(d)
-0,040
0,060
0,010
-0,015
-0,003
0,004
0,001
-0,001
0,000
0,000
(b-a)/2
5,000
2,500
1,250
0,625
0,313
0,156
0,078
0,039
0,020
0,010
x= 0,01
* Для решения нелинейного алгебраического
уравнения использован метод половинного
деления
9

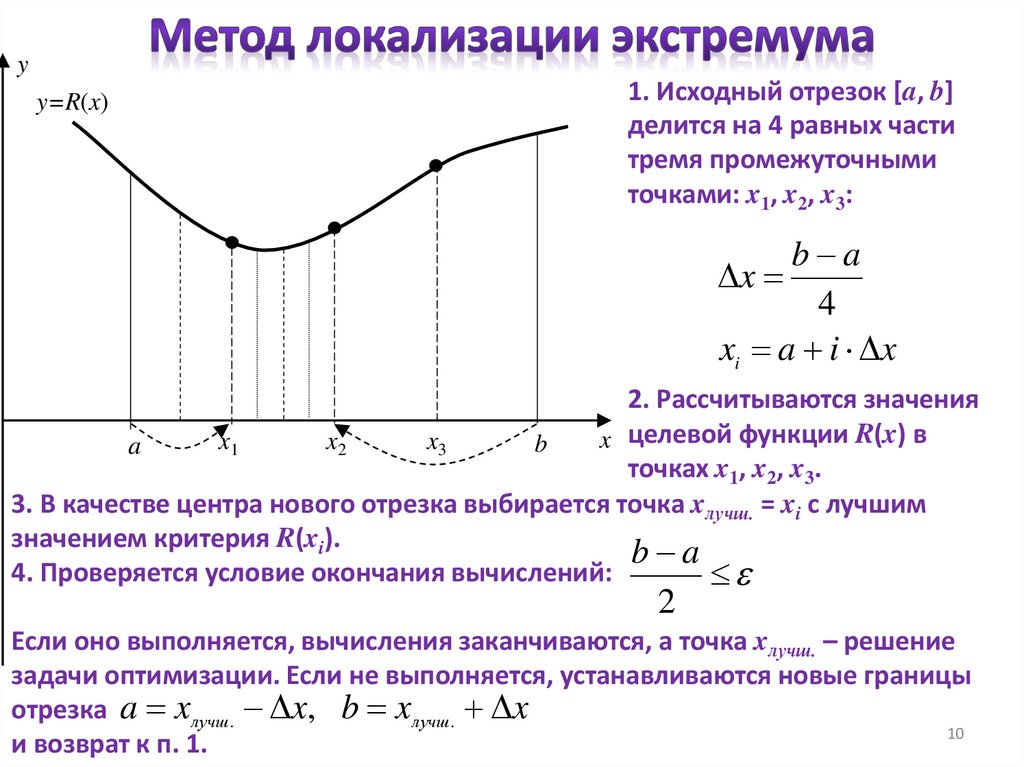
10.

y
y=R(x)
1. Исходный отрезок [a, b]
делится на 4 равных части
тремя промежуточными
точками: x1, x2, x3:
b a
x
4
xi a i x
2. Рассчитываются значения
x целевой функции R(x) в
x3
x1
x2
b
a
точках x1, x2, x3.
3. В качестве центра нового отрезка выбирается точка xлучш. = xi с лучшим
значением критерия R(xi).
b a
4. Проверяется условие окончания вычислений:
2
Если оно выполняется, вычисления заканчиваются, а точка xлучш. – решение
задачи оптимизации. Если не выполняется, устанавливаются новые границы
отрезка a x лучш . x, b x лучш . x
10
и возврат к п. 1.

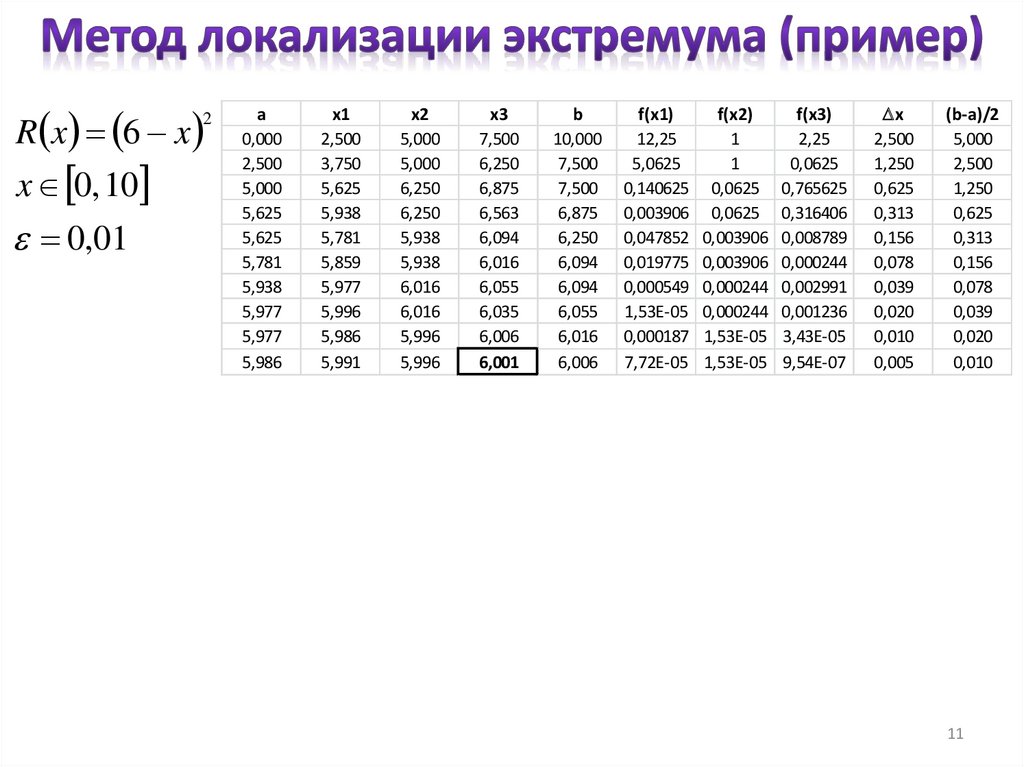
11.

R x 6 x
2
x 0, 10
0,01
a
0,000
2,500
5,000
5,625
5,625
5,781
5,938
5,977
5,977
5,986
x1
2,500
3,750
5,625
5,938
5,781
5,859
5,977
5,996
5,986
5,991
x2
5,000
5,000
6,250
6,250
5,938
5,938
6,016
6,016
5,996
5,996
x3
7,500
6,250
6,875
6,563
6,094
6,016
6,055
6,035
6,006
6,001
b
10,000
7,500
7,500
6,875
6,250
6,094
6,094
6,055
6,016
6,006
f(x1)
12,25
5,0625
0,140625
0,003906
0,047852
0,019775
0,000549
1,53E-05
0,000187
7,72E-05
f(x2)
1
1
0,0625
0,0625
0,003906
0,003906
0,000244
0,000244
1,53E-05
1,53E-05
f(x3)
2,25
0,0625
0,765625
0,316406
0,008789
0,000244
0,002991
0,001236
3,43E-05
9,54E-07
x
2,500
1,250
0,625
0,313
0,156
0,078
0,039
0,020
0,010
0,005
(b-a)/2
5,000
2,500
1,250
0,625
0,313
0,156
0,078
0,039
0,020
0,010
11

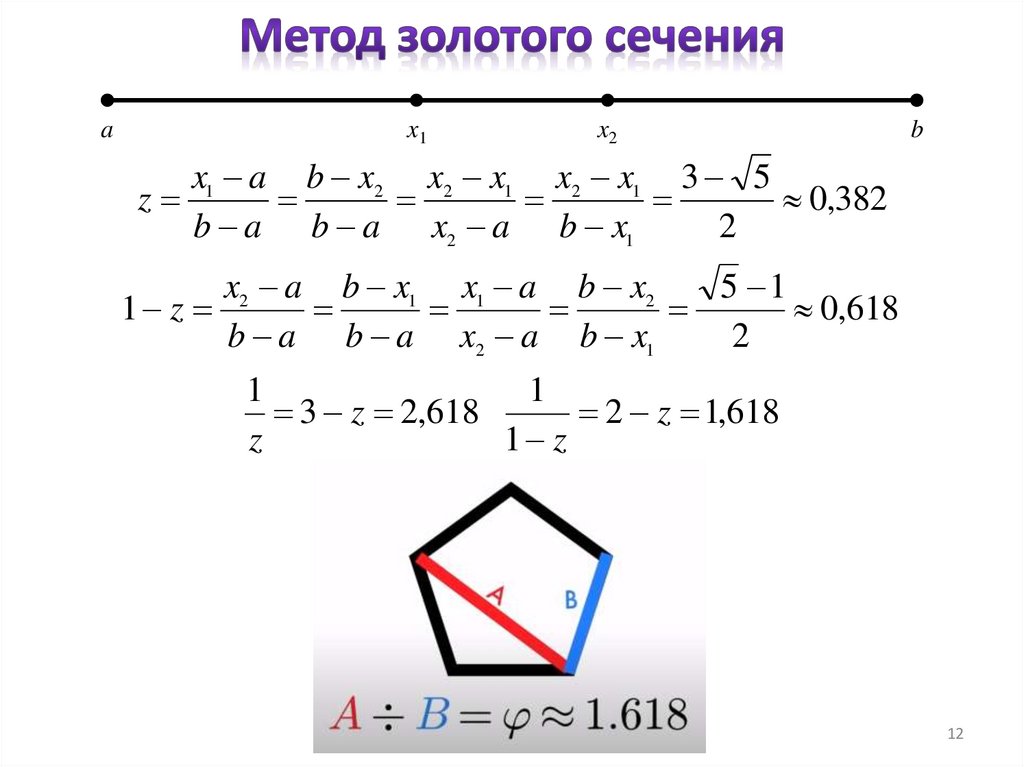
12.

a
x1
x2
b
x1 a b x2 x2 x1 x2 x1 3 5
z
0,382
b a b a x2 a b x1
2
x2 a b x1 x1 a b x2
5 1
1 z
0,618
b a b a x2 a b x1
2
1
1
3 z 2,618
2 z 1,618
z
1 z
12

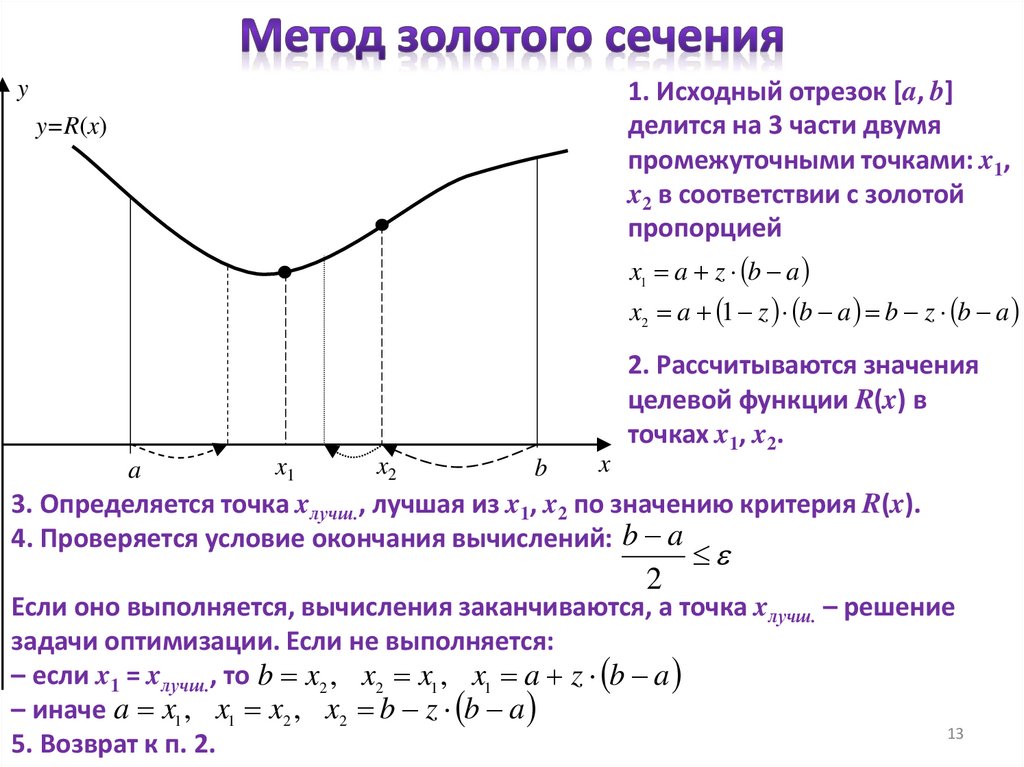
13.

1. Исходный отрезок [a, b]
делится на 3 части двумя
промежуточными точками: x1,
x2 в соответствии с золотой
пропорцией
y
y=R(x)
x1 a z b a
x2 a 1 z b a b z b a
2. Рассчитываются значения
целевой функции R(x) в
точках x1, x2.
a
x1
x2
b
x
3. Определяется точка xлучш., лучшая из x1, x2 по значению критерия R(x).
4. Проверяется условие окончания вычислений: b a
2
Если оно выполняется, вычисления заканчиваются, а точка xлучш. – решение
задачи оптимизации. Если не выполняется:
– если x1 = xлучш., то b x2 , x2 x1 , x1 a z b a
– иначе a x1 , x1 x2 , x2 b z b a
13
5. Возврат к п. 2.

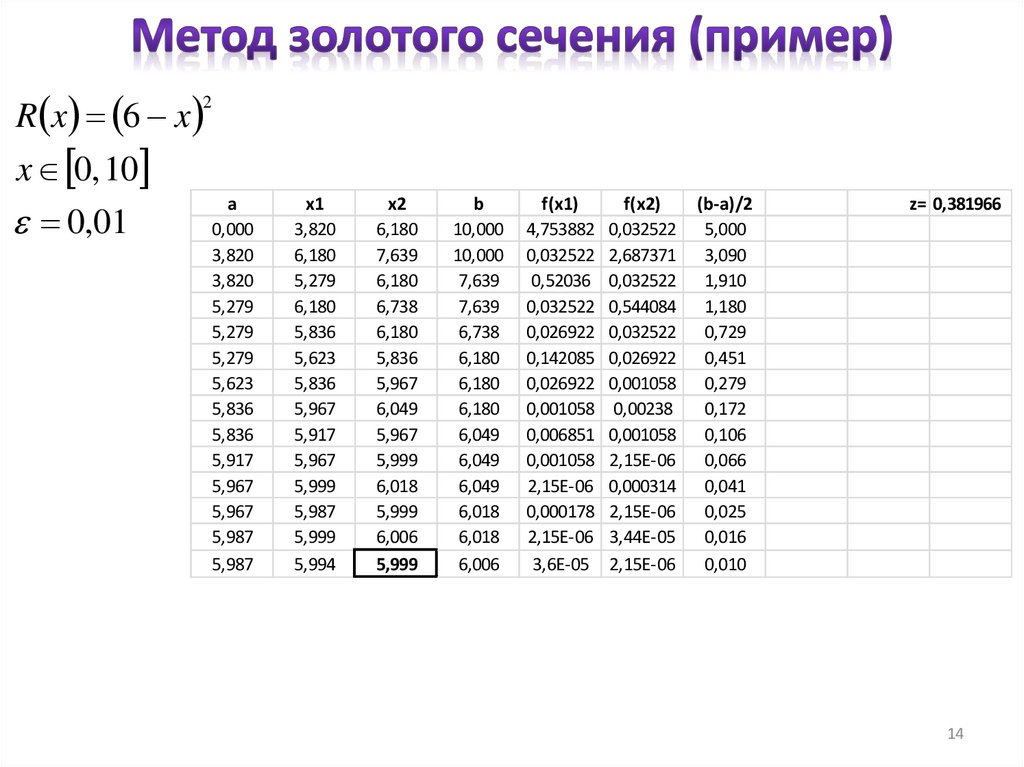
14.

R x 6 x
2
x 0, 10
0,01
a
0,000
3,820
3,820
5,279
5,279
5,279
5,623
5,836
5,836
5,917
5,967
5,967
5,987
5,987
x1
3,820
6,180
5,279
6,180
5,836
5,623
5,836
5,967
5,917
5,967
5,999
5,987
5,999
5,994
x2
6,180
7,639
6,180
6,738
6,180
5,836
5,967
6,049
5,967
5,999
6,018
5,999
6,006
5,999
b
10,000
10,000
7,639
7,639
6,738
6,180
6,180
6,180
6,049
6,049
6,049
6,018
6,018
6,006
f(x1)
4,753882
0,032522
0,52036
0,032522
0,026922
0,142085
0,026922
0,001058
0,006851
0,001058
2,15E-06
0,000178
2,15E-06
3,6E-05
f(x2)
0,032522
2,687371
0,032522
0,544084
0,032522
0,026922
0,001058
0,00238
0,001058
2,15E-06
0,000314
2,15E-06
3,44E-05
2,15E-06
(b-a)/2
5,000
3,090
1,910
1,180
0,729
0,451
0,279
0,172
0,106
0,066
0,041
0,025
0,016
0,010
z= 0,381966
14

15.

S 0
1
2
3
4
5
6
…
10
11
12
FS 1
1
2
3
5
8
13
…
89
144
233
FS-1/FS
-
1,000
0,500
0,667
0,600
0,625
0,615
…
0,618
0,618
0,618
FS-2/FS
-
-
0,500
0,333
0,400
0,375
0,385
…
0,382
0,382
0,382
z 0,382
1 z 0,618
1
3 z 2,618
z
1
2 z 1,618
1 z
Приближённое определение числа Фибоначчи FS по его номеру в
последовательности (формула Бине):
2 z
z 2
3 2z
S 1
FS
S 1
15

16.

1. Определяется пороговое число Фибоначчи FS, удовлетворяющее условию:
где N
b a
FS 1 N FS
.
2. Рассчитывается шаг поиска точки оптимума: x
b a
.
FS
3. На шаге расчёта с номером k исходный отрезок [a, b] делится на 3 части
двумя промежуточными точками x1, x2 в соответствии с соотношениями:
k
x1 a x FS k 1
x2
k
a x FS k
Определяются значения критерия: R(x1), R(x2).
4. Если x1 лучше, чем x2, то b x2 , x2 x1 ,
иначе a x1 , x1 x2 .
5. Процедура продолжается с п. 3 до тех пор, пока FS k FS k 1.
Решение – лучшая из координат x1, x2 во время последней проверки.
16

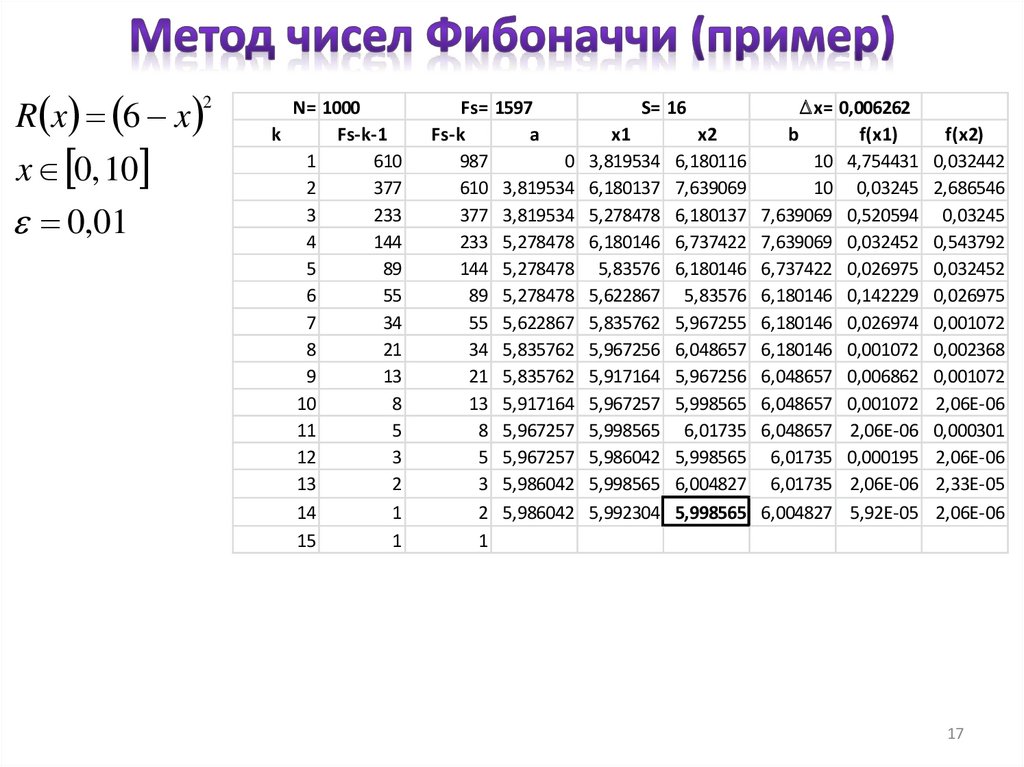
17.

R x 6 x
2
x 0, 10
0,01
N= 1000
k
Fs-k-1
1
610
2
377
3
233
4
144
5
89
6
55
7
34
8
21
9
13
10
8
11
5
12
3
13
2
14
1
15
1
Fs= 1597
Fs-k
a
987
0
610 3,819534
377 3,819534
233 5,278478
144 5,278478
89 5,278478
55 5,622867
34 5,835762
21 5,835762
13 5,917164
8 5,967257
5 5,967257
3 5,986042
2 5,986042
1
S= 16
x1
3,819534
6,180137
5,278478
6,180146
5,83576
5,622867
5,835762
5,967256
5,917164
5,967257
5,998565
5,986042
5,998565
5,992304
x2
6,180116
7,639069
6,180137
6,737422
6,180146
5,83576
5,967255
6,048657
5,967256
5,998565
6,01735
5,998565
6,004827
5,998565
x= 0,006262
b
f(x1)
10 4,754431
10 0,03245
7,639069 0,520594
7,639069 0,032452
6,737422 0,026975
6,180146 0,142229
6,180146 0,026974
6,180146 0,001072
6,048657 0,006862
6,048657 0,001072
6,048657 2,06E-06
6,01735 0,000195
6,01735 2,06E-06
6,004827 5,92E-05
f(x2)
0,032442
2,686546
0,03245
0,543792
0,032452
0,026975
0,001072
0,002368
0,001072
2,06E-06
0,000301
2,06E-06
2,33E-05
2,06E-06
17

18.

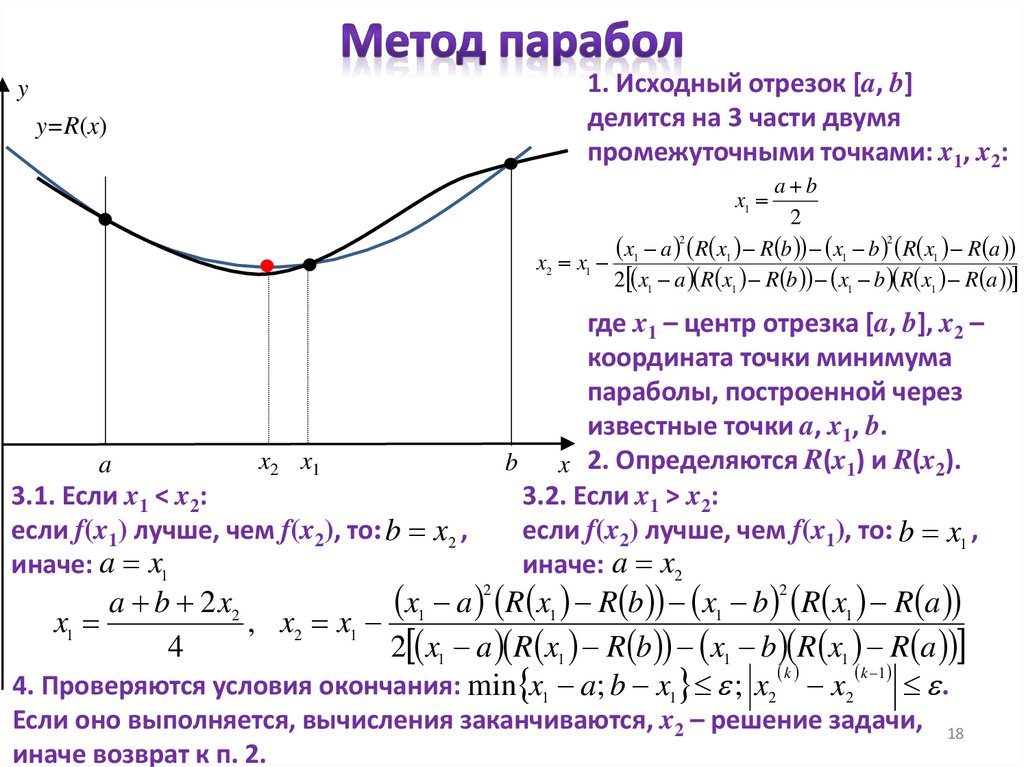
1. Исходный отрезок [a, b]
делится на 3 части двумя
промежуточными точками: x1, x2:
y
y=R(x)
a b
2
2
2
x1 a R x1 R b x1 b R x1 R a
x2 x1
2 x1 a R x1 R b x1 b R x1 R a
x1
a
где x1 – центр отрезка [a, b], x2 –
координата точки минимума
параболы, построенной через
известные точки a, x1, b.
b
x 2. Определяются R(x1) и R(x2).
3.2. Если x1 > x2:
если f(x2) лучше, чем f(x1), то: b x1 ,
иначе: a x2
x2 x1
3.1. Если x1 < x2:
если f(x1) лучше, чем f(x2), то: b x2 ,
иначе: a x1
a b 2 x2
x1 a R x1 R b x1 b R x1 R a
x1
, x2 x1
4
2 x1 a R x1 R b x1 b R x1 R a
k
k 1
4. Проверяются условия окончания: min x1 a; b x1 ; x2 x2
.
2
2
Если оно выполняется, вычисления заканчиваются, x2 – решение задачи,
иначе возврат к п. 2.
18

19.

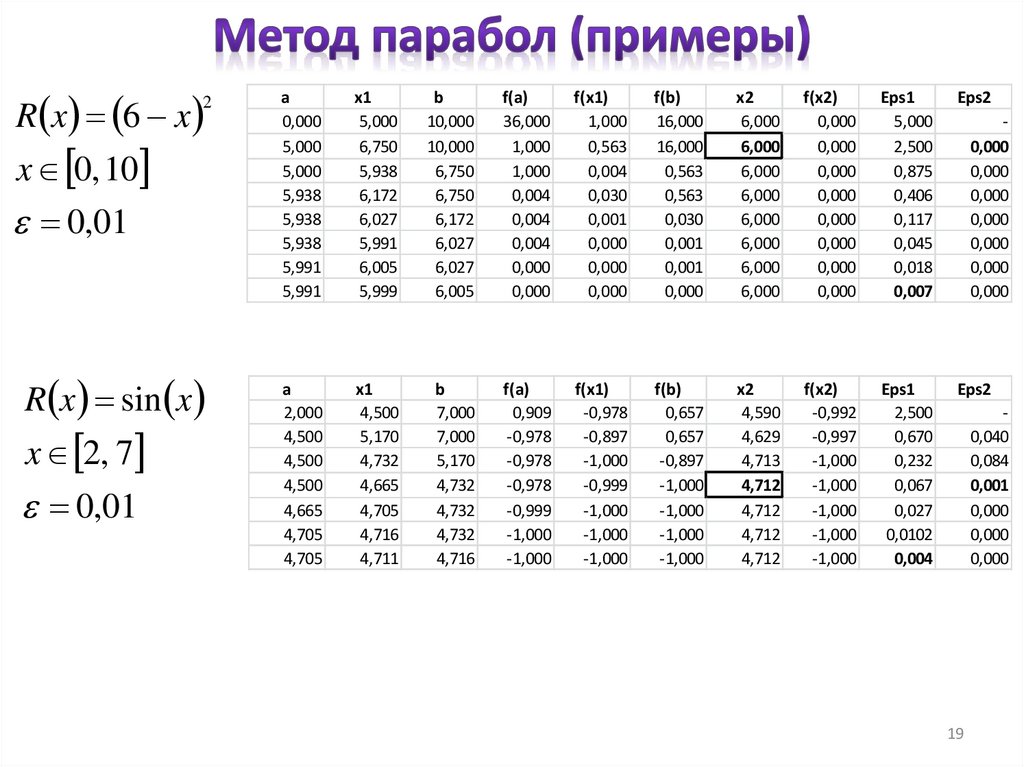
R x 6 x
2
x 0, 10
0,01
R x sin x
x 2, 7
0,01
a
0,000
5,000
5,000
5,938
5,938
5,938
5,991
5,991
x1
5,000
6,750
5,938
6,172
6,027
5,991
6,005
5,999
b
10,000
10,000
6,750
6,750
6,172
6,027
6,027
6,005
f(a)
36,000
1,000
1,000
0,004
0,004
0,004
0,000
0,000
f(x1)
1,000
0,563
0,004
0,030
0,001
0,000
0,000
0,000
f(b)
16,000
16,000
0,563
0,563
0,030
0,001
0,001
0,000
x2
6,000
6,000
6,000
6,000
6,000
6,000
6,000
6,000
f(x2)
0,000
0,000
0,000
0,000
0,000
0,000
0,000
0,000
Eps1
5,000
2,500
0,875
0,406
0,117
0,045
0,018
0,007
Eps2
a
2,000
4,500
4,500
4,500
4,665
4,705
4,705
x1
4,500
5,170
4,732
4,665
4,705
4,716
4,711
b
7,000
7,000
5,170
4,732
4,732
4,732
4,716
f(a)
0,909
-0,978
-0,978
-0,978
-0,999
-1,000
-1,000
f(x1)
-0,978
-0,897
-1,000
-0,999
-1,000
-1,000
-1,000
f(b)
0,657
0,657
-0,897
-1,000
-1,000
-1,000
-1,000
x2
4,590
4,629
4,713
4,712
4,712
4,712
4,712
f(x2)
-0,992
-0,997
-1,000
-1,000
-1,000
-1,000
-1,000
Eps1
2,500
0,670
0,232
0,067
0,027
0,0102
0,004
Eps2
0,000
0,000
0,000
0,000
0,000
0,000
0,000
0,040
0,084
0,001
0,000
0,000
0,000
19

20.

y
y=R(x)
a
x1
x2
b
x
20

21.

Решить задачу минимизации всеми методами. N – номер варианта
лабораторного практикума.
R x exp a0 a1 x a2 x 2
1
N
a0
N
20
N
1 N 25
a1
20
N 15
a2
200
x 10, 10
0,01

22.

22