Similar presentations:
Математические основы анализа свойств систем и наблюдения их состояния (лекция № 17)
1.
Дисциплина1
ОСНОВЫ ТЕОРИИ СИСТЕМ И УПРАВЛЕНИЯ
Раздел №2. Основы теории систем
Тема №5. Математические основы анализа свойств систем и наблюдения их состояния
(лекция № 17)
Задача наблюдения состояния ДС
Учебные вопросы:
5.7 Постановка задачи наблюдения состояния ДС.
5.8 Основные принципы построения алгоритмов наблюдения в условиях
детерминированной среды для ЛДДС при линейных измерениях.
5.9 Интегральный алгоритм наблюдения. Концепция динамической
фильтрации.
2.
5.7 Постановка задачи наблюдения состояния ДС2
5.7.1 Общая математическая постановка проблемы наблюдения состояния
динамической системы
Проблема наблюдения состояния динамической системы является одной из
четырех фундаментальных проблем системных исследований.
Динамическая система в канонической форме задается общим выражением
{T,X,R,P,U,V,Y,N; , },
переходное отображение:
выходное отображение:
x(t ) (t, ,x( ), uT ,vT ),
y(t )= (t,x(t ), v(t )).
при рассмотрении проблемы наблюдения выходное отображение называется
также уравнением измерителя.
Композиция выходного и переходного отображений определяет
терминальное отображение:
y(t ) d (t, ,x( ), uT ,vT ) (t, (t, ,x( ), uT ,vT ), v(t )),
которое определяет некоторый оператор с параметром :
yT k ( ,x( ), uT ,vT ),
k ( , , , ) : X U V N ,
3.
Пусть в конкретном опыте средой реализовано некоторое конкретноедопустимое возмущающее воздействие vT V , в результате чего
зафиксирована соответствующая реакция:
3
y k (tÍ , x(tÍ ), uT ,vT ).
Дано:
– динамическая система Σ ;
– управляющее воздействие uT U ;
– характеристика возмущающей среды (типа α, β, γ или δ);
– множество моментов времени наблюдения T ;
– некоторый момент времени tН T .
Определить:
по заданному фрагменту y N соответствующей реакции системы
определить ее состояние в момент времени tН .
Отсюда следует, что решить проблему наблюдения – значит найти решение
относительно z X следующего операторного уравнения:
(*)
k (tÍ , z,uT ,vT ) y vT V
правая часть которого представляет собой измеренные значения реакции
системы на соответствующем интервале времени. В левой части этого
уравнения – неизвестное возмущающее воздействие, относительно которого
известно только, что оно принадлежит классу допустимых возмущений V и
формируется средой в соответствии с типом среды (α, β, γ , δ,).
4.
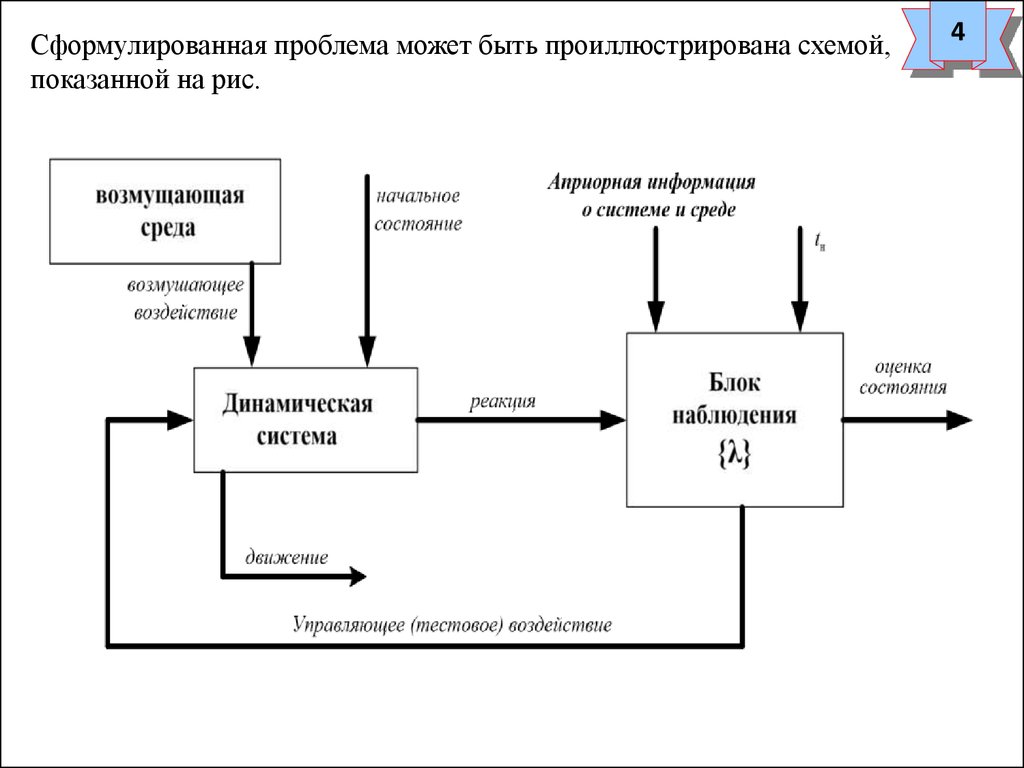
Сформулированная проблема может быть проиллюстрирована схемой,показанной на рис.
4
5.
5отсутствие возмущений (замкнутая ДС)
Условия наблюдения
(проблема идеального наблюдения)
состояния ДС
наличие возмущений (открытая ДС
стохастическая среда - β
целенаправленная среда - γ
Источник информации свободная реакция ДС
о состоянии
вынужденная реакция ДС
Характер момента
времени оценки (наблюдения)
неизвестная среда - δ
ретроспекция - С0
текущее оценивание - С1
прогноз (экстраполяция) - С2
непрерывные
Алгоритм обработки измерений
дискретные
обработка текущей информации
обработка полной выборки
Структура множества
моментов времени
ДС с непрерывным временем
ДС с дискретным временем
Характер переходного и Линейные ДС
выходного отображений Нелинейные ДС
Измерения
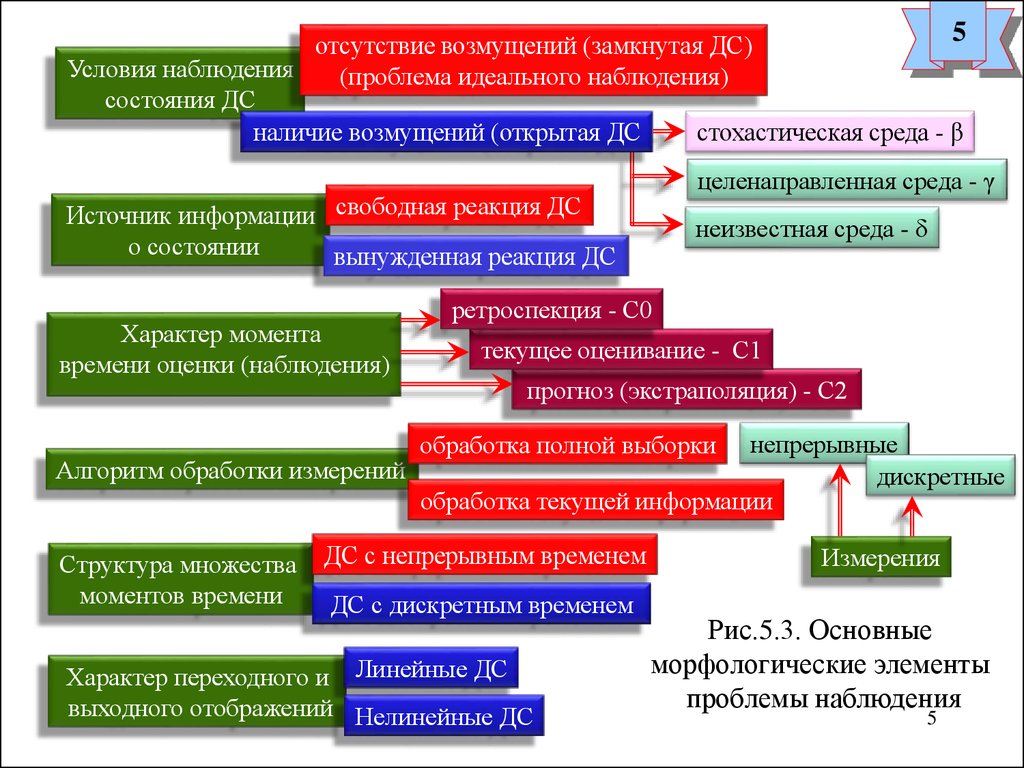
Рис.5.3. Основные
морфологические элементы
проблемы наблюдения
5
6.
5.8. Основные принципы построения алгоритмов наблюдения в условияхдетерминированной среды для ЛДДС при линейных измерениях.
6
1. Общая математическая постановка и качественный анализ проблемы
наблюдения состояния замкнутой динамической системы
Этот вариант проблемы наблюдения уже обсуждался в предыдущей теме, в п.
7.6. Напомним и уточним постановку задачи, считая систему обратимой.
Рассмотрим свободную реакцию замкнутой динамической системы, которая
определяется совокупностью переходного и выходного отображений :
x(t) 0ñâ (t, , x( )),
y(t)= 0 (t, x(t)),
и соответствующего терминального отображения:
y(t) d 0ñâ (t, , x( )) (t, 0ñâ (t, , x( ))).
Обозначим соответствующую динамическую систему через
0ñâ {T,X,Y, N; 0ñâ , 0 }.
Зафиксируем некоторый момент времени t1 T (t 0 ) и рассмотрим отрезок
реакции, отвечающий множеству моментов времени (t 0 , t1 ] T :
y : Y.
6
7.
В соответствии с общей постановкой задачи наблюдений п.5.7указанным отображениям можно соотнести оператор:
7
y k 0ñâ ( , x( )), k 0ñâ ( , ) : X N ,
действующий из одного гильбертова пространства в другое, и сформулировать
следующую проблему идеального наблюдения.
Пусть в конкретном опыте состоянию системы x(t Í ) , в котором она находилась в момент времени t Í , соответствует реакция
y k 0ñâ (t Í , x(t Í )).
Проблема идеального наблюдения состояния динамической системы
Пусть заданы:
- динамическая система 0ñâ (8.14);
- множество моментов времени наблюдения T;
- некоторый момент времени t Í T.
Требуется: по заданному фрагменту y N соответствующей реакции
системы определить ее состояние в момент времени t Í .
{ 0ñâ , t Í ; y } x(t Í ) ?
7
8.
5.9. Интегральный алгоритм идеального наблюдения состояниялинейной конечномерной дифференциальной динамической системы
8
Рассмотрим задачу идеального наблюдения для замкнутой линейной системы
с конечномерным пространством состояний, уравнения которой имеют следующий вид:
x=A(t)x
y=C(t)x
Здесь A(t) - квадратная n n - матрица, C(t) - прямоугольная m n - матрица ( 1 m<n ). Будем полагать, что элементы этих матриц представляют собой
вещественные функции, определенные и имеющие непрерывные производные
n-1 – порядка на T=R1.
Если в момент времени t Í система находилась в состоянии x(t Í ) , то это однозначно определяет реакцию системы на всей вещественной оси моментов времени:
y(t) C(t) (t, t Í )x(t Í ),
- линейный оператор, действующий из конечномерного гильбертова пространства состояний в гильбертово пространство реакций.
Уточним задачу наблюдения. Предположим, что реакция фиксируется (измеряется) на некотором интервале (t 0 , t] , т.е. измерения производятся непрерывно и требуется найти состояние системы в конце этого интервала, т.е. t Í t.
В этом случае реакция системы может быть представлена в виде:
9.
9y ( ) C( ) ( , t)x(t), (t 0 , t].
Рассматриваемая задача заключается в нахождении решении уравнения:
C( ) ( , t)z y ( ), (t 0 , t],
относительно z X .
Будем предполагать, что условие полной наблюдаемости в данном случае выполнено (!), тогда решение операторного уравнения существует, единственно и совпадает с искомым истинным состоянием x(t) .
Найдем это решение. С этой целью введем следующую вещественную функцию от z :
t
1
T
p(t,z) y ( ) C( ) ( , t)z Q( ) y ( ) C( ) ( , t)z d , (*)
2 t0
где Q( ) - произвольная положительно-определенная m n - матричная функция
от . При этом подынтегральное выражение является положительно определенной формой от выражения в квадратных скобках и достигает минимального значения при равенстве этого выражения нулю.
В связи с этим рассмотрим гладкую задачу на безусловный минимум:
p(t,z) min
z X
9
10.
Найдем указанный минимум. С этой целью используем известное необходимоеусловие экстремума гладкой функции при отсутствии ограничений:
10
gradp(t,z)
p(t,z)
0,
z
где 0 - нулевая вектор-строка. Дифференцируя функцию (8.23) по вектору z ,
запишем условие (8.24) в виде:
p(t,z)
zT P(t) y T ( )Q( )C( ) ( , t)d 0.
z
t0
t
Здесь P(t) - квадратная n n - матрица, определяемая формулой:
t
P(t) T ( , t)CT ( )Q( )C( ) ( , t)d . (**)
t0
Можно показать, что если условие полной наблюдаемости для системы
выполнено, то при любой положительно-определенной матрице Q( )
матрица (**) является неособенной. Отсюда следует, что искомое решение
задачи (минималь) имеет следующий вид:
t
z x(t) P 1 (t) T ( , t)CT ( )Q( )y ( )d .
t0
(***)
10
11.
Эта формула определяет интегральный алгоритм наблюдения, при использовании которогоискомая оценка состояния формируется в резуtÍ t
льтате интегрирования реакции в целом, зафиy
ксированной на интервале (t 0 , t], подвергИнтегральный z x(t)
нутой некоторому специальному матричному
t блок наблюдения
оценка
реакция
{λ}
преобразованию (рис.5.4). Истинность полученсостояния
ного решения легко проверяется непосредственРис.5.4
ной подстановкой в (***).
В результате проведения вычислений по формуле интегрального алгоритма
(***) находится истинное состояние системы в момент времени t Í t, т.е. в
момент окончания измерений. Если необходимо узнать состояние системы в любой другой момент времени, то вследствие обратимости системы это состояние
может быть найдено по формуле:
Априорная информация
о системе
x(t Í ) (t Í , t)x(t),
для любого значения t Í - как в прошлом, при t Í t (ретроспективное наблюдение), так и будущем, при t Í t (прогноз состояния).
Таким образом, задача идеального линейного наблюдения при непрерывном
поступлении измерительной информации и обработки соответствующей отрезка
реакции решена полностью.
11









 mathematics
mathematics informatics
informatics








