Similar presentations:
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
1.
Обработка экспериментальных данныхЛекция 6:
Регрессионный и корреляционный анализ.
Нелинейная зависимость
Преподаватель: Аникеева Александра Евгеньевна
2.
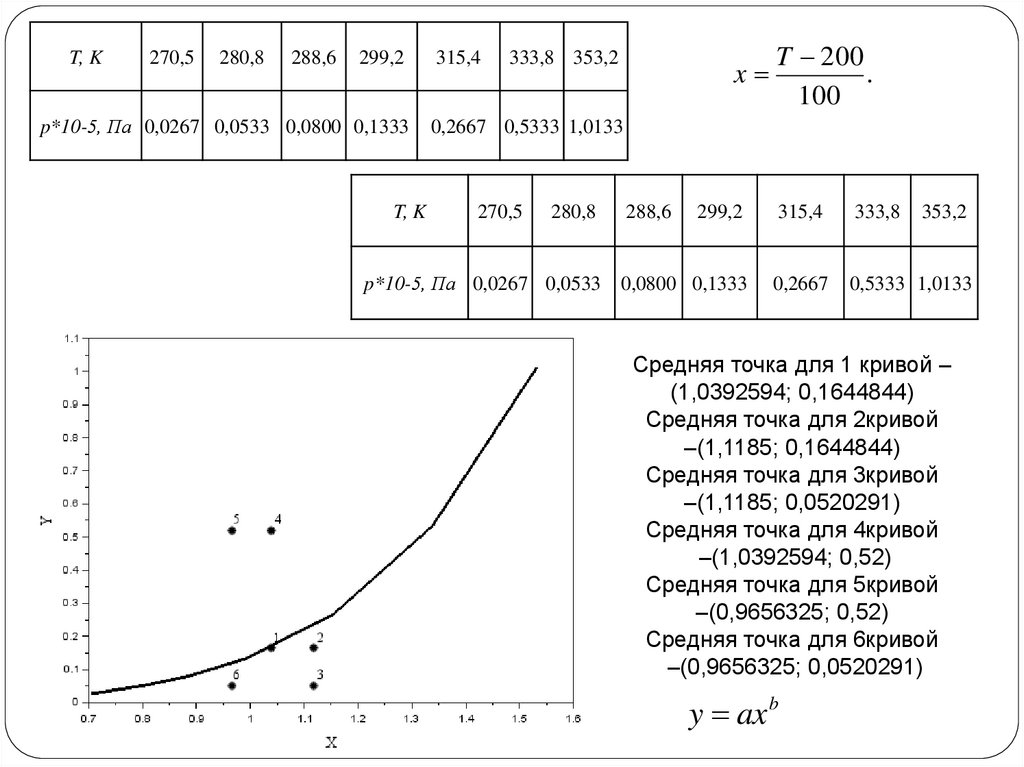
Метод средних точек3.
T, K270,5
280,8
288,6
299,2
p*10-5, Па 0,0267 0,0533 0,0800 0,1333
T, K
315,4
333,8 353,2
x
T 200
.
100
0,2667 0,5333 1,0133
270,5
280,8
288,6
299,2
315,4
333,8
353,2
p*10-5, Па 0,0267 0,0533 0,0800 0,1333
0,2667
0,5333 1,0133
Средняя точка для 1 кривой –
(1,0392594; 0,1644844)
Средняя точка для 2кривой
–(1,1185; 0,1644844)
Средняя точка для 3кривой
–(1,1185; 0,0520291)
Средняя точка для 4кривой
–(1,0392594; 0,52)
Средняя точка для 5кривой
–(0,9656325; 0,52)
Средняя точка для 6кривой
–(0,9656325; 0,0520291)
y ax b
4.
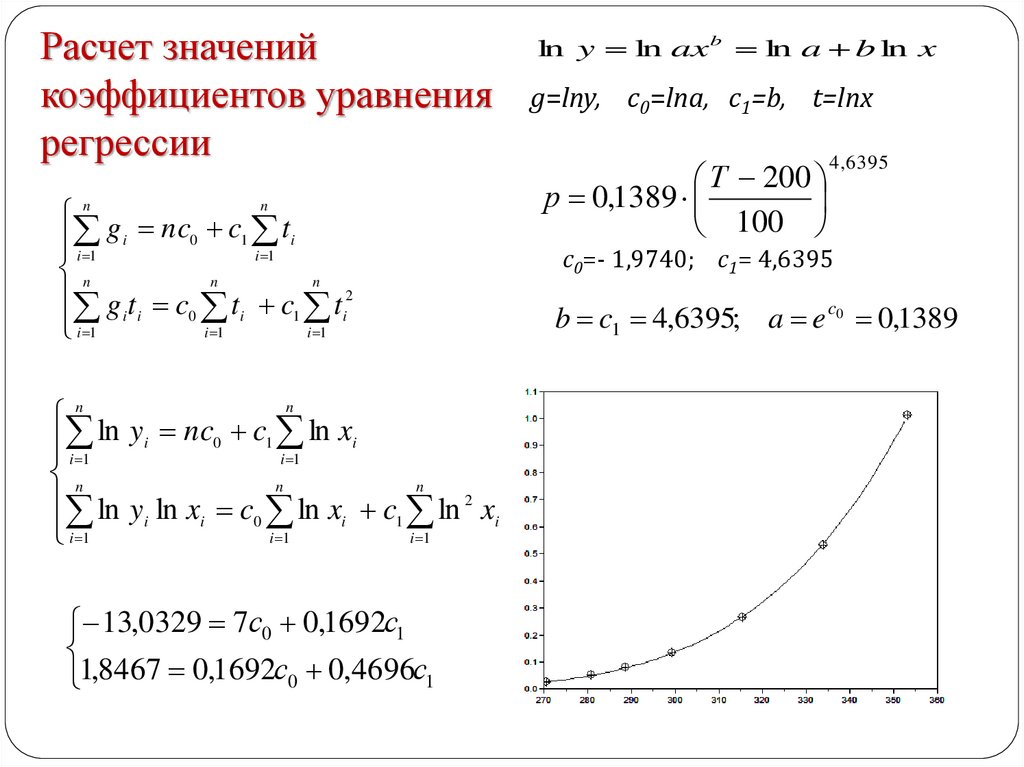
Расчет значенийкоэффициентов уравнения
регрессии
n g nc c n t
i
0
1 i
i 1
i 1
n
n
n
g i ti c0 ti c1 ti2
i 1
i 1
i 1
n ln y nc c n ln x
i
0
1
i
i 1
i 1
n
n
n
ln yi ln xi c0 ln xi c1 ln 2 xi
i 1
i 1
i 1
13,0329 7с0 0,1692с1
1,8467 0,1692с0 0,4696с1
ln y ln ax b ln a b ln x
g=lny, c0=lna, c1=b, t=lnx
Т 200
р 0,1389
100
4, 6395
с0=- 1,9740; с1= 4,6395
b c1 4,6395; a e c0 0,1389
5.
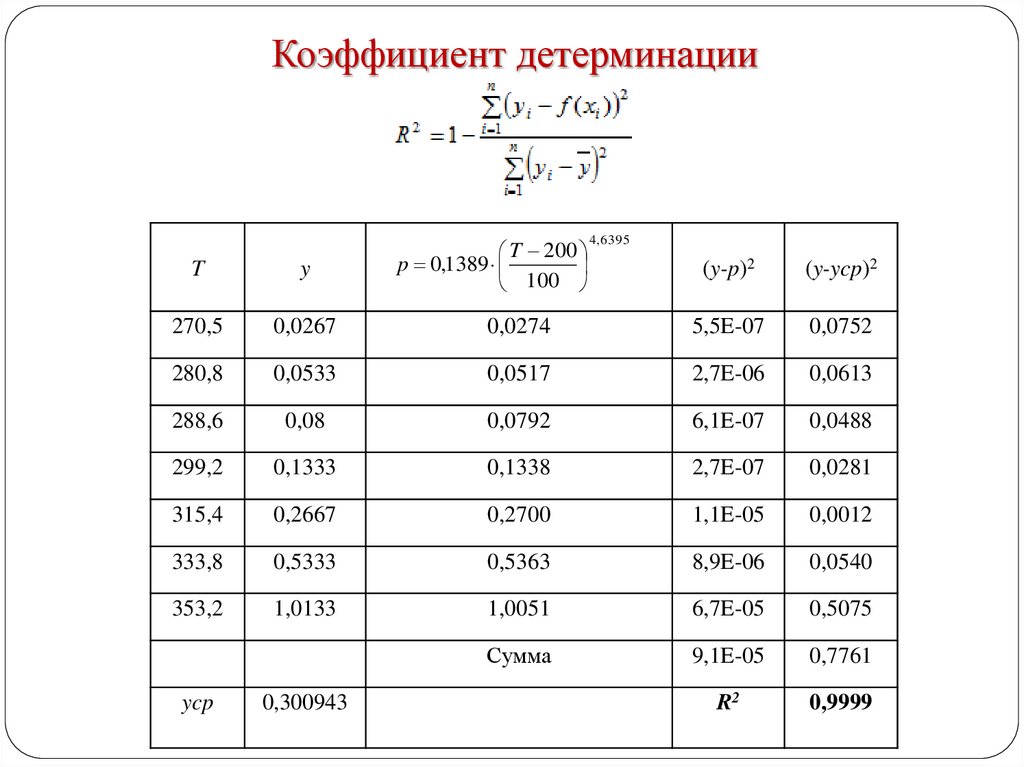
Коэффициент детерминацииT 200
p 0,1389
100
4, 6395
(y-p)2
(y-ycp)2
0,0274
5,5E-07
0,0752
0,0533
0,0517
2,7E-06
0,0613
288,6
0,08
0,0792
6,1E-07
0,0488
299,2
0,1333
0,1338
2,7E-07
0,0281
315,4
0,2667
0,2700
1,1E-05
0,0012
333,8
0,5333
0,5363
8,9E-06
0,0540
353,2
1,0133
1,0051
6,7E-05
0,5075
Сумма
9,1E-05
0,7761
R2
0,9999
T
y
270,5
0,0267
280,8
ycp
0,300943
6.
Проверка адекватности модели по критериюФишера-Снедекора
Проверим гипотезу об адекватности полученной сглаживающей кривой
исходным данным по критерию Фишера при уровне значимости α=0,05.
Fвыб
R 2 (n 2) 0,9999 (7 2)
55013,3
2
1 R
1 0,9999
Здесь R2 – коэффициент детерминации, n=7. По числу степеней
свободы k1=1 и k2=n-2=5 найдем критическое значение Fкр= 6,607891.
Так как Fвыб>Fкр , делаем вывод о том, что полученное уравнение
экспоненциальной регрессии:
4.6395
Т 200
р 0,1389
100
статистически значимо описывает результаты эксперимента.
7.
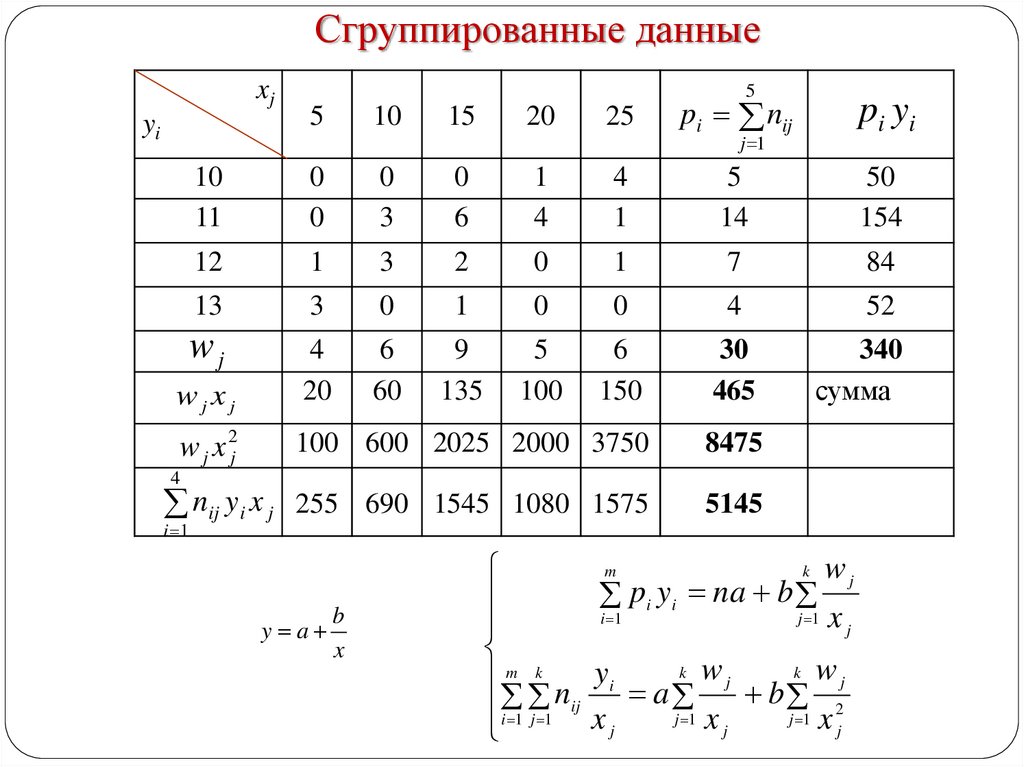
Сгруппированные данныеxj
5
5
10
15
20
25
pi nij
pi yi
10
11
0
0
0
3
0
6
1
4
4
1
5
14
50
154
12
1
3
2
0
1
7
84
13
3
0
1
0
0
4
52
wj
wj xj
4
20
6
60
9
135
5
100
6
150
30
465
w j x 2j
100 600 2025 2000 3750
8475
nij yi x j 255 690 1545 1080 1575
5145
yi
j 1
340
сумма
4
i 1
y a
b
x
m
k w
j
p
y
na
b
i i
i 1
j 1 x
j
m k
k w
k w
yi
j
b 2j
nij a
i 1 j 1 x j
j 1 x
j 1 x
j
j
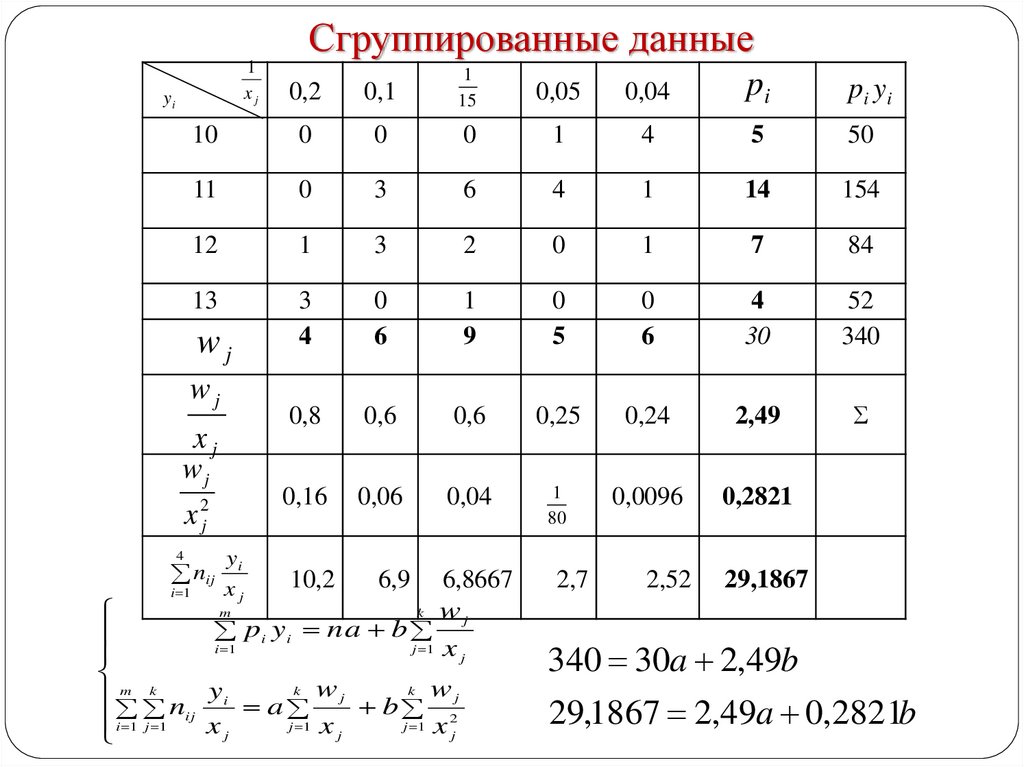
8.
Сгруппированные данные1
xj
0,2
0,1
1
15
0,05
0,04
pi
pi yi
10
0
0
0
1
4
5
50
11
0
3
6
4
1
14
154
12
1
3
2
0
1
7
84
13
3
4
0
6
1
9
0
5
0
6
4
30
52
340
0,8
0,6
0,6
0,25
0,24
2,49
Σ
0,16
0,06
0,04
1
80
0,0096
0,2821
10,2
6,9
yi
wj
wj
xj
wj
x 2j
4
nij
i 1
yi
xj
6,8667
m
k w
j
p
y
na
b
i i
i 1
j 1 x
j
m k
k w
k w
y
j
b 2j
nij i a
i 1 j 1
j 1 x
j 1 x
xj
j
j
2,7
2,52
29,1867
340 30a 2,49b
29,1867 2,49a 0,2821b
9.
Коэффициент детерминации.
f (x ) y w
k
12,81542723
f ( x) 10,269653
x
R2
yi y pi 24,6667
m
i 1
y
2
2
j
j 1
y
m
i 1
y
2
i
j
pi
4
m y
i
i 1
i
n
R2
340
11,3333
30
12,3883
0,50223
24,6667
xj
5
10
15
20
25
f(xj)
12,8327
11,5512
11,1240
10,9104
10,7823
wj
4
6
9
5
6
( f ( x j y) 2 w j
8,9929
0,2848
0,3943
0,8943
1,8220
5
( f ( x j y) 2 w j
j 1
Уравнение регрессии
12,3883
12,81542723
x
объясняет примерно 50% всей вариации зависимой величины Y.
f ( x) 10,269653
10.
Проверка адекватностиxj
S
2
повт
Qповт
Qадекв
2
; S адекв
30 5
5 2
5
10
15
20
25
12,833
11,551
11,124
10,910
10,782
12,75
11,5
11,444
10,8
10,5
wj
4
6
9
5
6
( f (x j y j )2 w j
0,0274
0,0157
0,9241
0,0610
0,4781
f (x j )
yj
5
2
Qпов т 10,77222
Qадекв f ( x j ) y j w j (12,83274 12,75) 2 4
j 1
1,506
(11,5512 11,5) 2 6 (11,12401 11,44444) 2 9 (10,91042 10,8) 2 5
(10,78227 10,5) 2 6 1,506211
0,502070352
f выб
1,165197
0,430889
fкр(0,05, 3, 25)=2,991
10,77222
0,430889;
25
1,506211
0,502070352.
3
2
S пов
т
2
S адекв
Поскольку fвыб<fкрделаем вывод об адекватности модели выборочным данным.
11.
Определение силы криволинейной связиКорреляционное отношение η
Общая дисперсия
2
yx
Sy
Межгрупповая дисперсия
S y2
2
Sy
1 k
( y j y) 2 w j
n j 1
1m
S ( y i y ) 2 pi
n i 1
2
y
2
m
1
1
S
0,463148
0,750525
S y2 ( yi y) 2 pi 24,66667 0,82222 yx 2y
0,82222
Sy
n i 1
30
i 1
S yx2
S
S y2
2
yx
1m
( yi y xi ) 2
n i 1
Значение
η=0
0 < η < 0,2
0,2 ≤ η < 0,3
Характер связи
Отсутствует
Очень слабая
Слабая
Значение
0,5 ≤ η < 0,7
0,7 ≤ η < 0,9
0,9 ≤ η < 1
Характер связи
Заметная
Сильная
Весьма сильная
0,3 ≤ η < 0,5
Умеренная
η=1
Функциональная







 mathematics
mathematics








