Similar presentations:
Тригонометрические уравнения
1. Тригонометрические уравнения
sin x=a, cos x=a, tg x=a, ctg x=ahttp://aida.ucoz.ru
2. Арксинус, арккосинус, арктангенс, арккотангенс числа
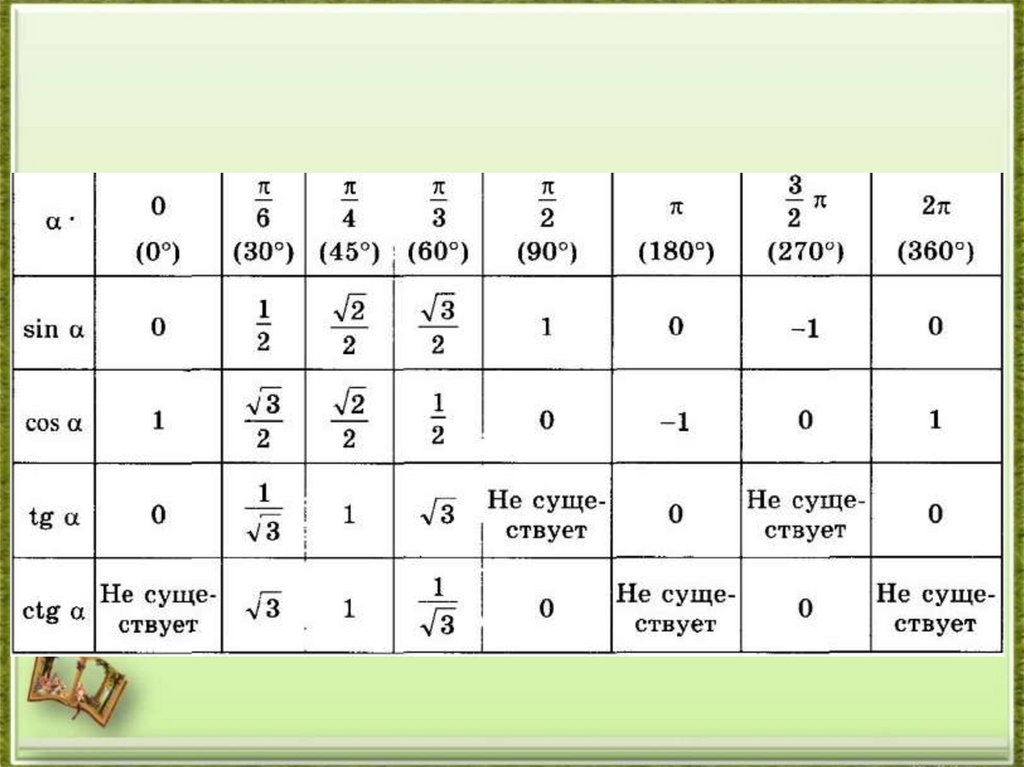
3.
4.
5.
6.
7. Свойства с отрицательными значениями
8. Практическая работа. Арккосинус
9. Арксинус
10. Арктангенс, арккотангенс
11. Решение простейших тригонометрических уравнений.
12.
13. Решение уравнения cos х = a
Решается с помощью единичной окружностиy
a
0
-1
1
2. Отметить точку а на оси
абсцисс (линии косинусов – ось x)
3. Провести перпендикуляр
из этой точки к окружности
4. Отметить точки
пересечения перпендикуляра
с окружностью.
x 5. Полученные числа–
решения уравнения cosх = a.
6. Записать общее решение
уравнения.
n
-х1
Запись +2πn означает, что из точки x
на окружности можно сделать сколько
угодно полных оборотов и все равно
получим точку x)
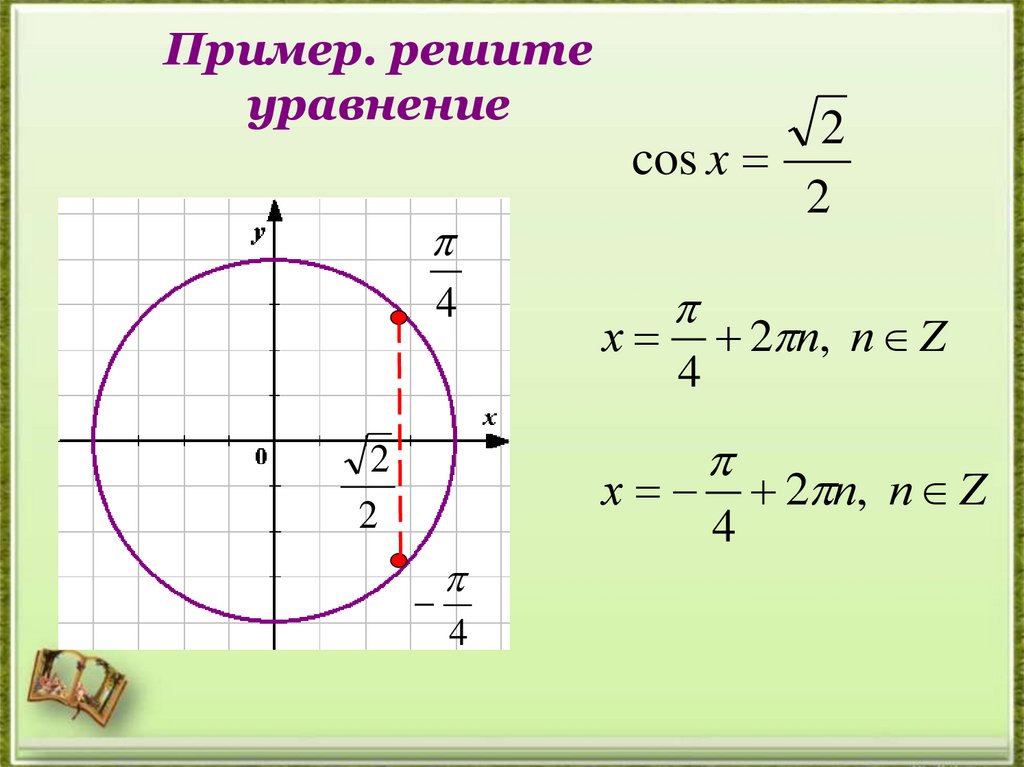
14. Пример. решите уравнение
42
2
2
cos x
2
х
4
х
4
2 п, п Z
4
2 п, п Z
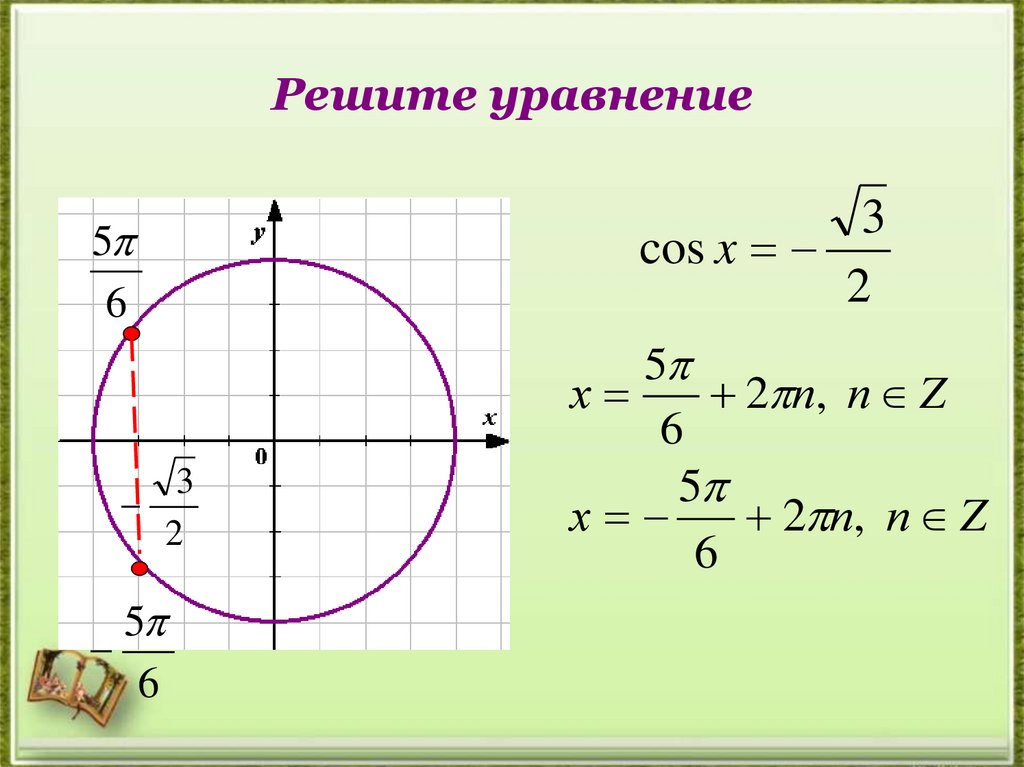
15. Решите уравнение
56
3
2
5
6
3
cos x
2
5
х
2 п, п Z
6
5
х
2 п, п Z
6
16.
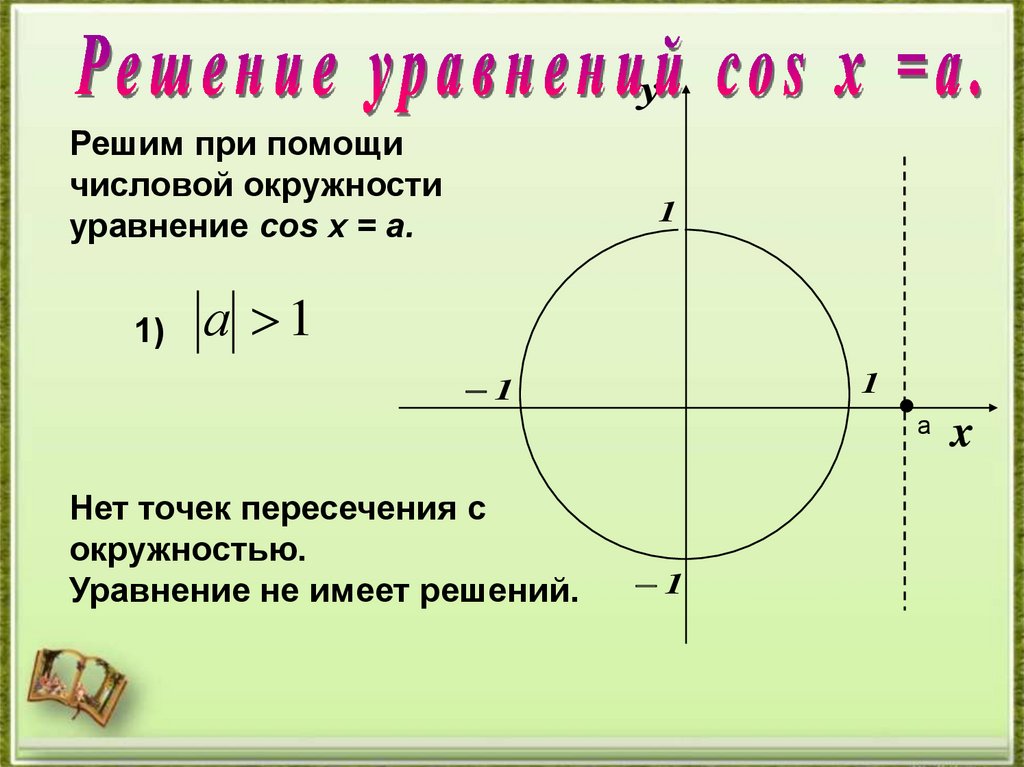
yРешим при помощи
числовой окружности
уравнение cos х = a.
1)
1
а 1
1
1
а
Нет точек пересечения с
окружностью.
Уравнение не имеет решений.
1
x
17.
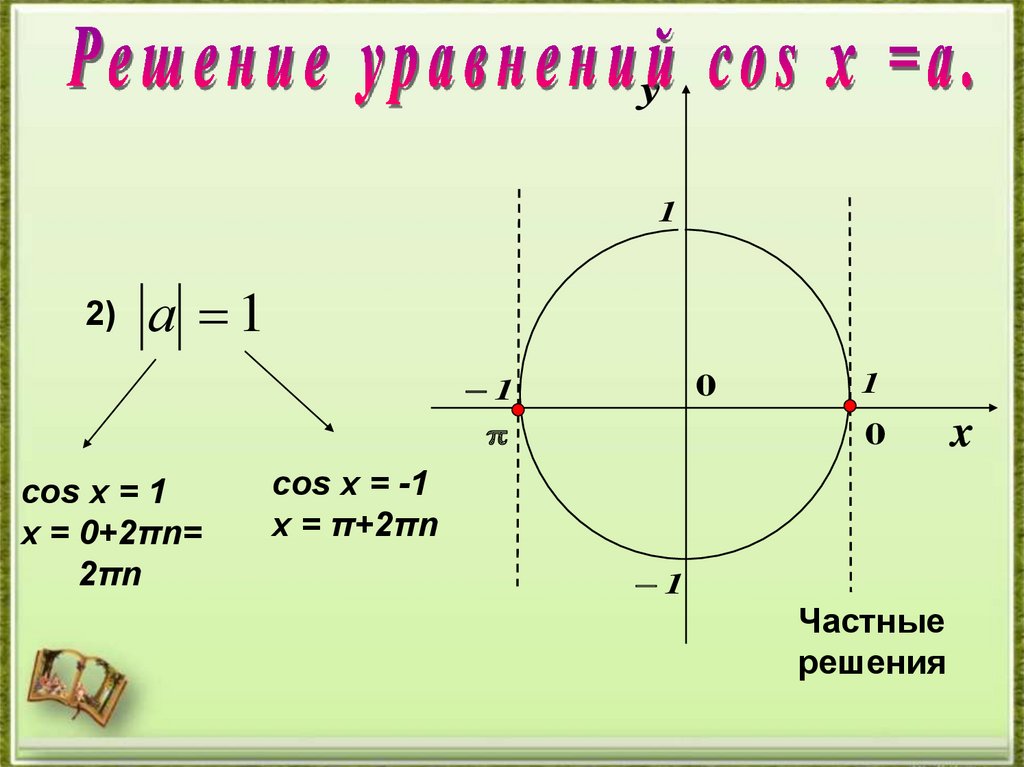
y1
2)
а 1
1
0
cos х = 1
х = 0+2πn=
2πn
1
0
cos х = -1
х = π+2πn
1
Частные
решения
x
18.
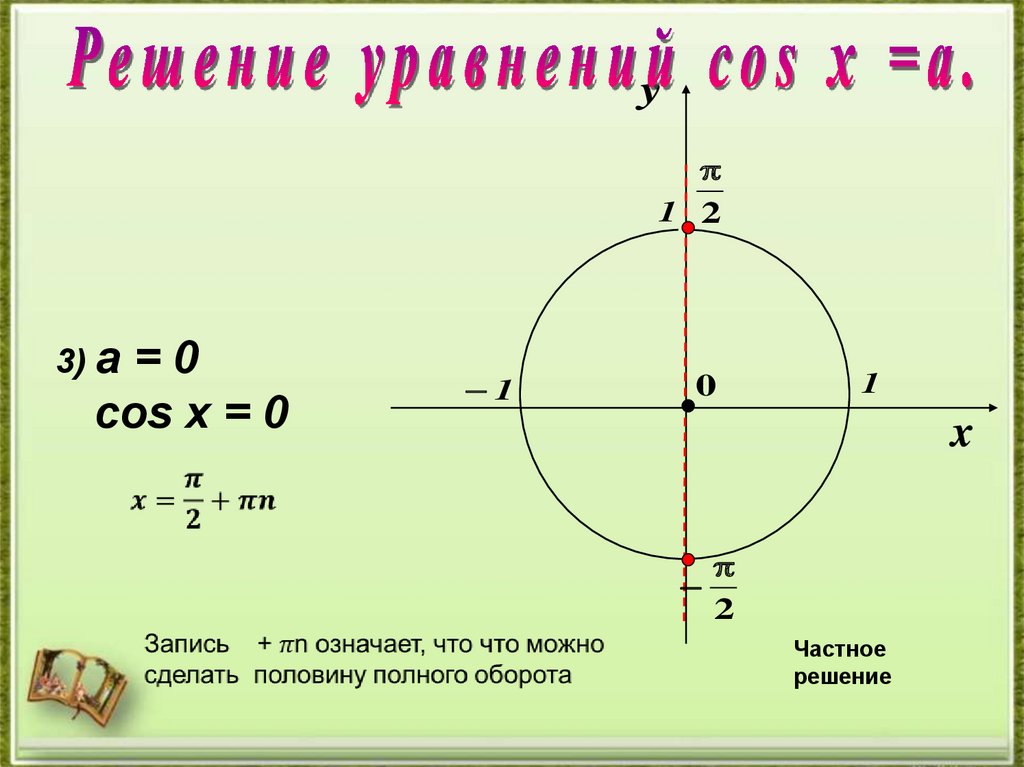
y1 2
3) а
=0
сos x = 0
1
0
1
x
2
Частное
решение
19.
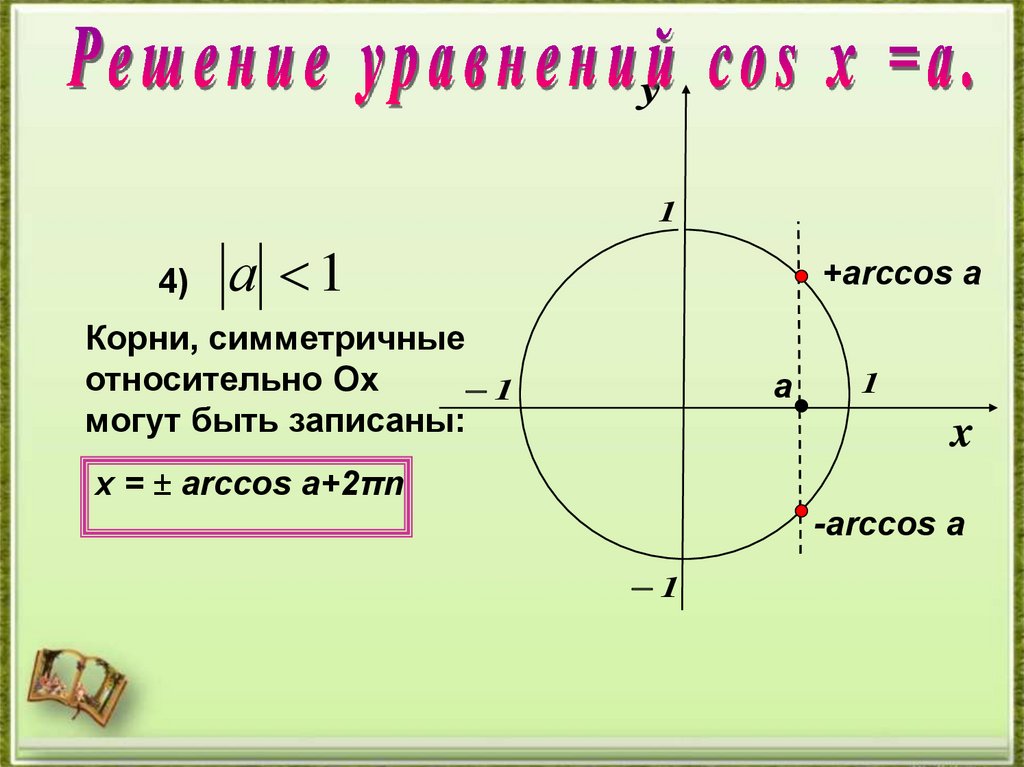
y1
4)
а 1
+arccos а
Корни, симметричные
относительно Оx
1
могут быть записаны:
а
1
x
х = ± arccos a+2πn
-arccos а
1
20. Практическая работа
21.
Решение уравнения sin х = aРешается с помощью единичной окружности
2. Отметить точку а на оси ординат (линии синусов – ось y)
3. Провести перпендикуляр из этой точки к окружности
4. Отметить точки пересечения перпендикуляра с
окружностью.
5. Полученные числа– решения уравнения sin х = a.
6. Записать общее решение уравнения.
x1 = arсsin a + 2πk, n ϵ Z
x 2 = π - arсsin a + 2πk, n ϵ Z. Или
Запись +2πk означает, что из точки x на окружности можно
сделать сколько угодно полных оборотов и все равно получим
точку x)
22. Решение уравнения вида: sin x = a
a)при -1< x < 1 имеет две серии корней
x1 = arсsin a + 2πn, n ϵ Z
x 2 = π - arсsin a + 2πn, n ϵ Z.
Или
б) при а = 1 имеет одну серию решений
sin х = 1
x=
+ 2πn, n ϵ Z
в) при а = -1 имеет одну серию решений
sin х = -1
x= + 2πn, n ϵ Z;
г) при а = 0 :
sin х = 0
x = πn, n ϵ Z ;
д) при а > 1 и a < -1
уравнение не имеет корней.
23. Решите уравнение
,,sin х =
24. Решите уравнение
(;,,;
Решите
2) sin х = -
2
2
уравнение
25. Задание Найти корни уравнения:
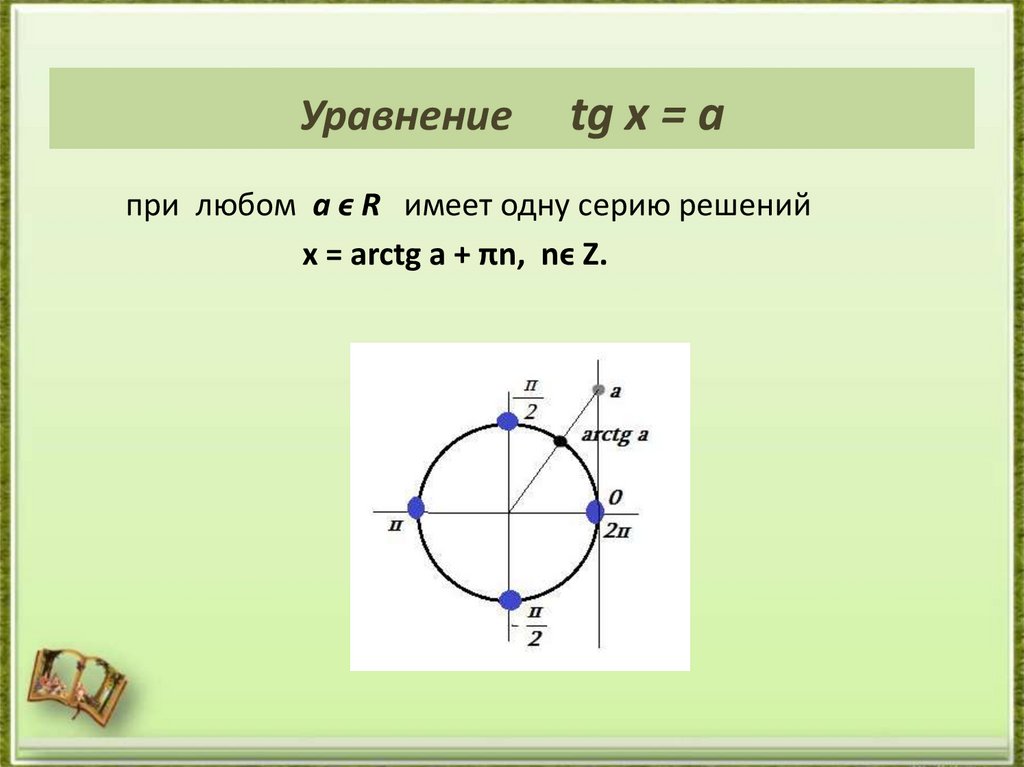
Задание Найти корни уравнения:26. Уравнение tg x = a
при любом а ϵ R имеет одну серию решенийх = аrctg a + πn, nϵ Z.
27. Решите уравнение
Решите1) tg x =
х = аrctg
x=
уравнение
2) tg x = -
+ πn, nϵ Z.
+ πn, nϵ Z.
х = аrctg(x=-
) + πn, nϵ Z,
+ πn, nϵ Z.
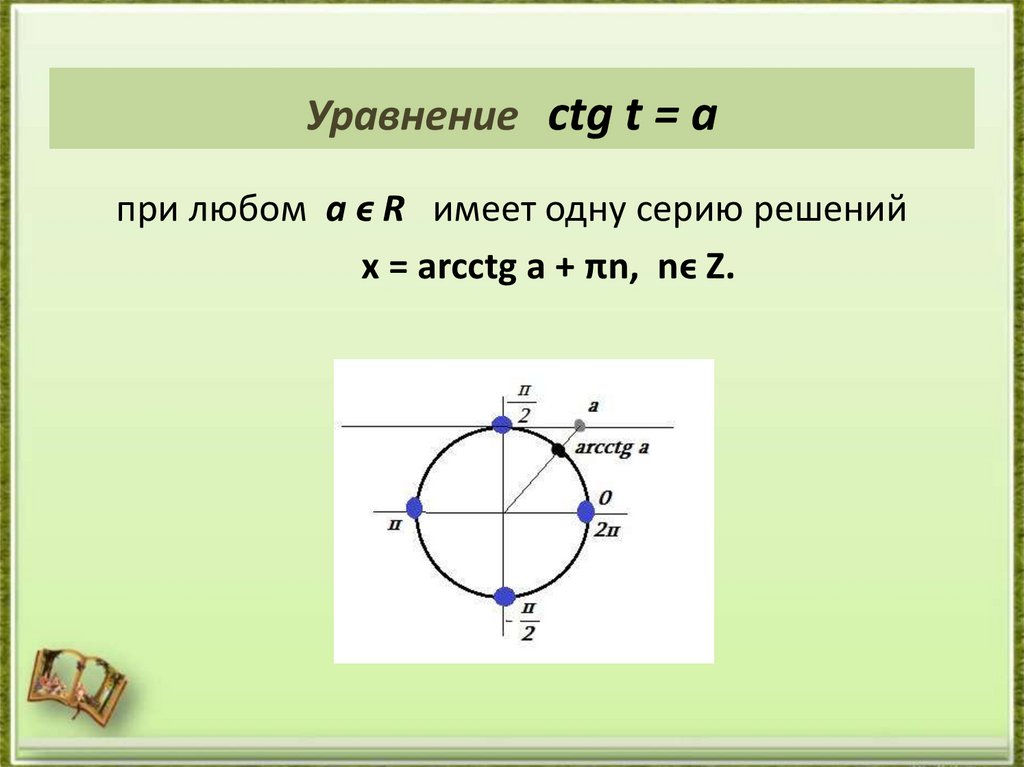
28. Уравнение ctg t = a
при любом а ϵ R имеет одну серию решенийх = аrcctg a + πn, nϵ Z.
29. Решите уравнение
Решите1) ctg x = 1
уравнение
2)
ctg x = - 1
х = аrcctg 1 + πn, nϵ Z,
х = аrcctg ( -1) + πn, nϵ Z
х=
х = π - аrcctg 1 + πn, nϵ Z
+ πn, nϵ Z.
х=
+ πn, nϵ Z.
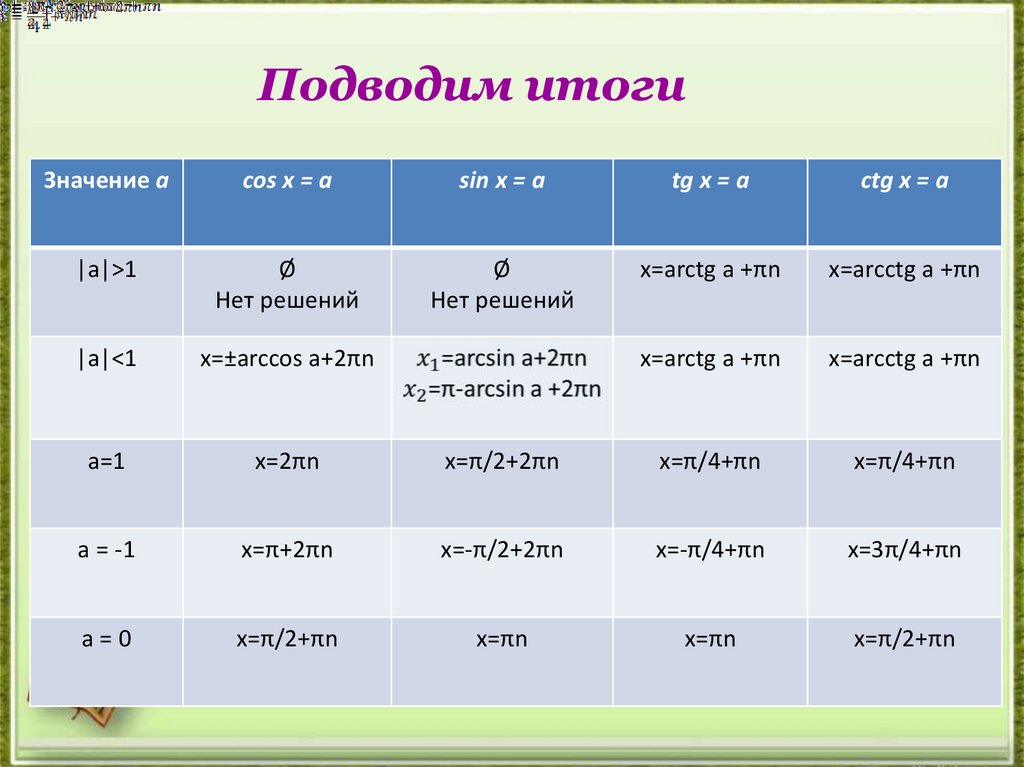
30. Подводим итоги
Значение аcos x = a
sin x = a
tg x = a
ctg x = a
|a|>1
Ø
Нет решений
Ø
Нет решений
x=arctg a +πn
x=arcctg a +πn
|a|<1
x=±arccos a+2πn
x=arctg a +πn
x=arcctg a +πn
a=1
x=2πn
x=π/2+2πn
x=π/4+πn
x=π/4+πn
a = -1
x=π+2πn
x=-π/2+2πn
x=-π/4+πn
x=3π/4+πn
a=0
x=π/2+πn
x=πn
x=πn
x=π/2+πn
31. Домашнее задание.
Выучить формулы для решениятригонометрических уравнений





















 mathematics
mathematics








