Тригонометрические уравнения

1.

Тригонометрические
уравнения
http://aida.ucoz.ru

2.

Определение.
• Уравнения вида f(x) = а, где а – данное
число, а f(x) – одна из тригонометрических
функций,
называются
простейшими
тригонометрическими уравнениями.

3.

Решение простейших
тригонометрических уравнений.

4.

Чтобы успешно решать простейшие
тригонометрические уравнения нужно
1) уметь отмечать точки на числовой
окружности;
2) уметь определять значения синуса, косинуса,
тангенса и котангенса для точек числовой
окружности;
3) знать свойства основных
тригонометрических функций;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
15.12.2020
4

5.

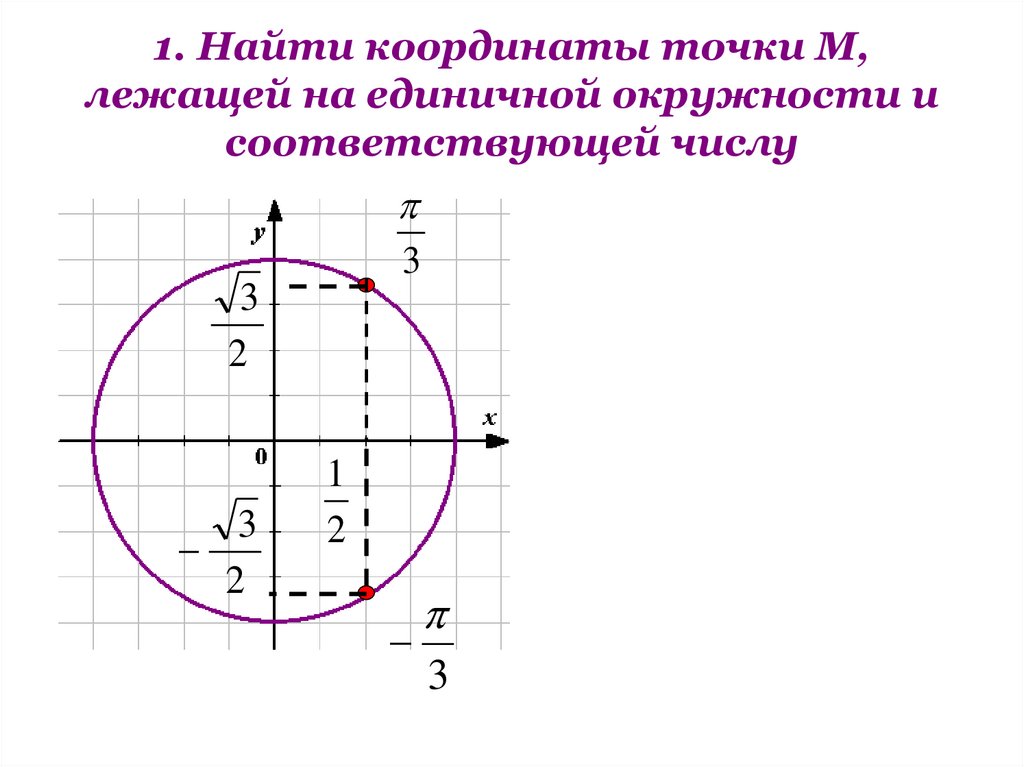
1. Найти координаты точки М,
лежащей на единичной окружности и
соответствующей числу
3
3
2
3
2
1
2
3

6.

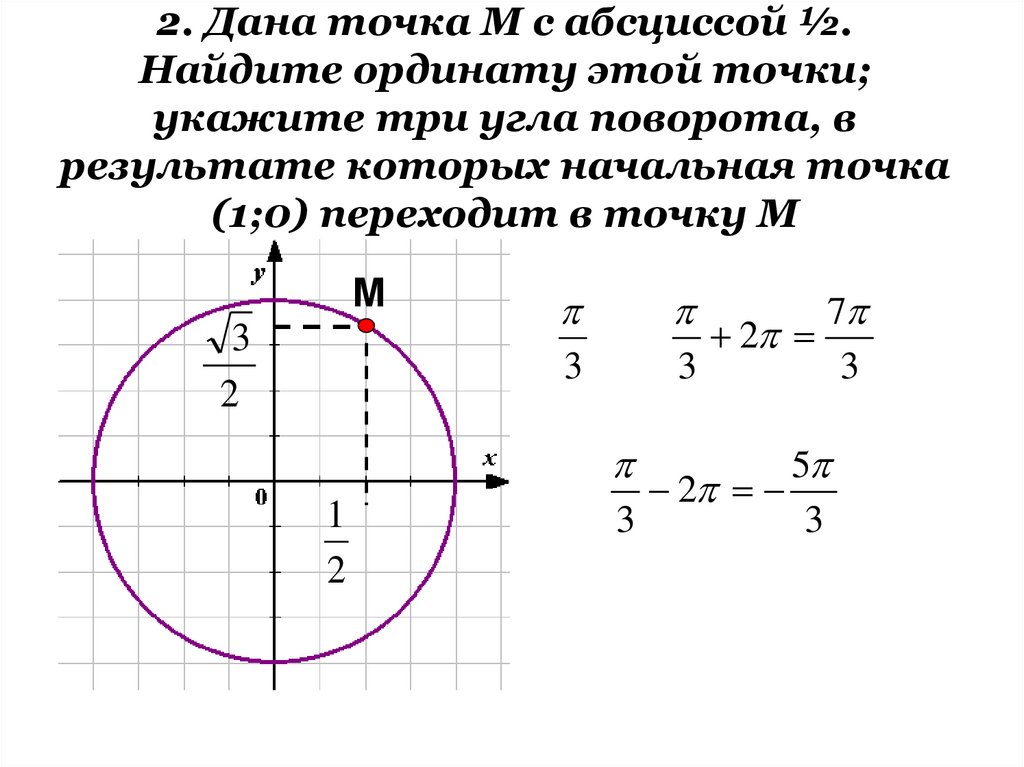
2. Дана точка М с абсциссой ½.
Найдите ординату этой точки;
укажите три угла поворота, в
результате которых начальная точка
(1;0) переходит в точку М
М
3
2
7
2
3
3
3
1
2
5
2
3
3

7.

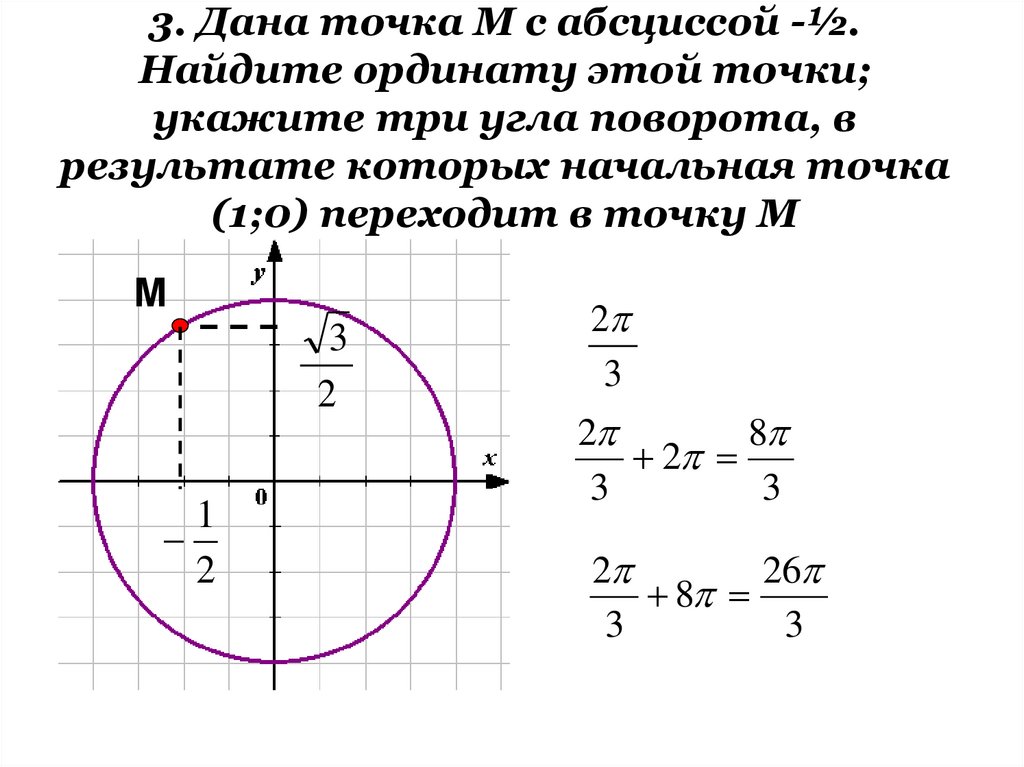
3. Дана точка М с абсциссой -½.
Найдите ординату этой точки;
укажите три угла поворота, в
результате которых начальная точка
(1;0) переходит в точку М
М
3
2
1
2
2
3
2
8
2
3
3
2
26
8
3
3

8.

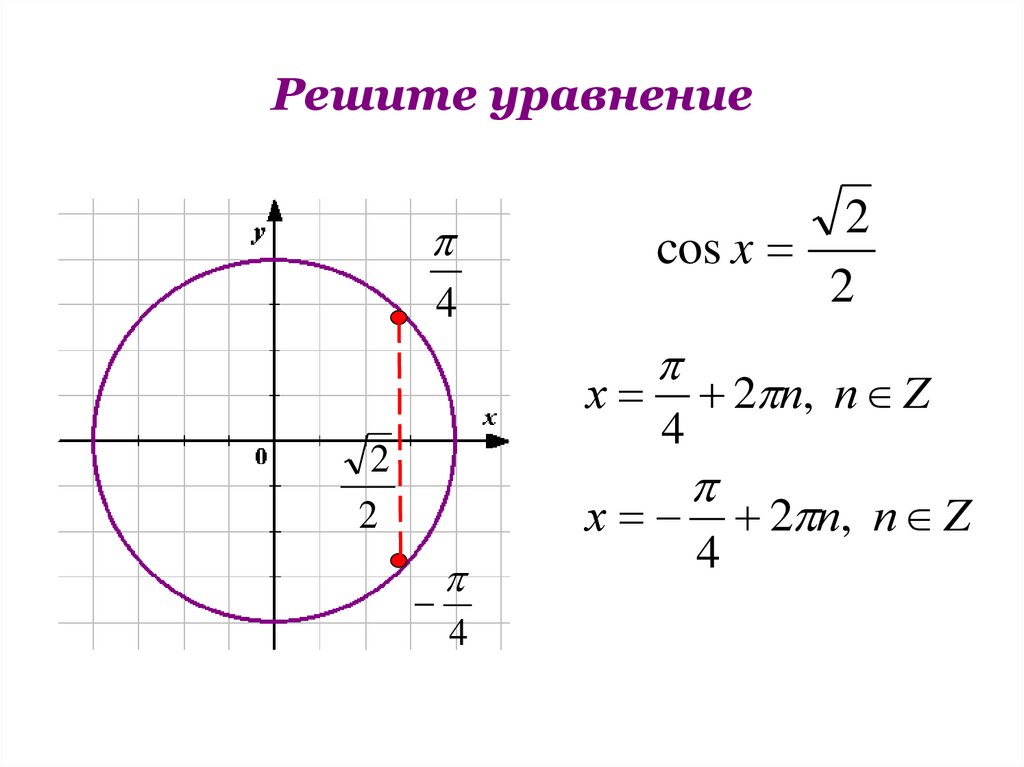
Решите уравнение
2
cos x
2
4
х
2
2
4
х
4
2 п, п Z
4
2 п, п Z

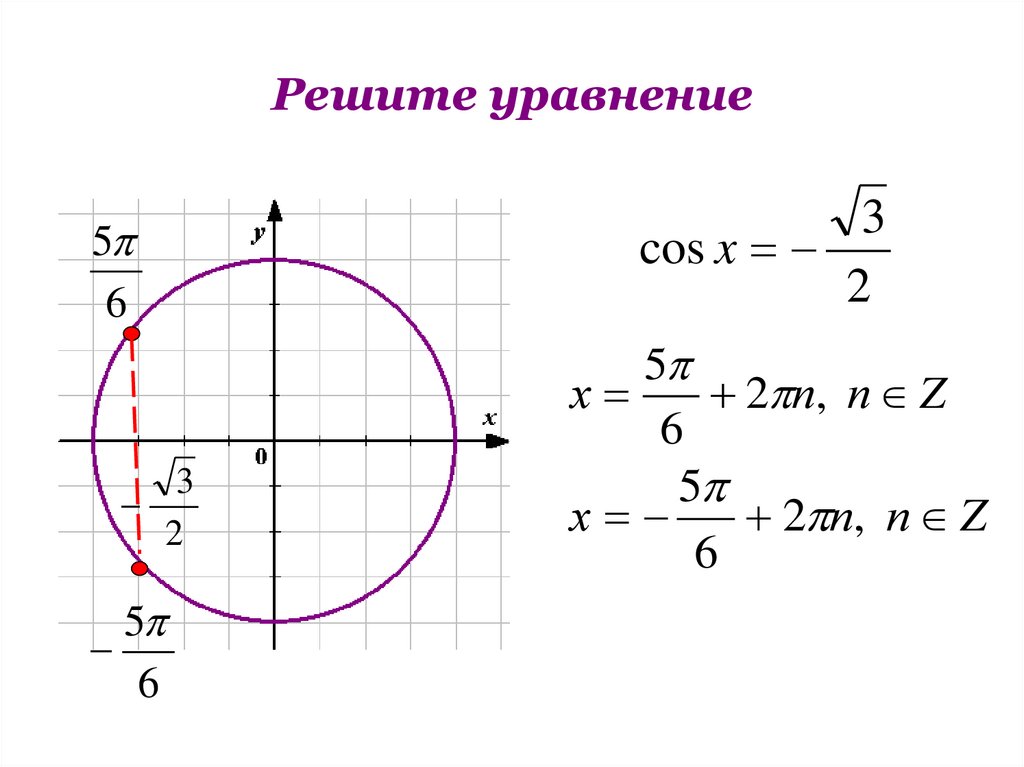
9.

Решите уравнение
5
6
3
2
5
6
3
cos x
2
5
х
2 п, п Z
6
5
х
2 п, п Z
6

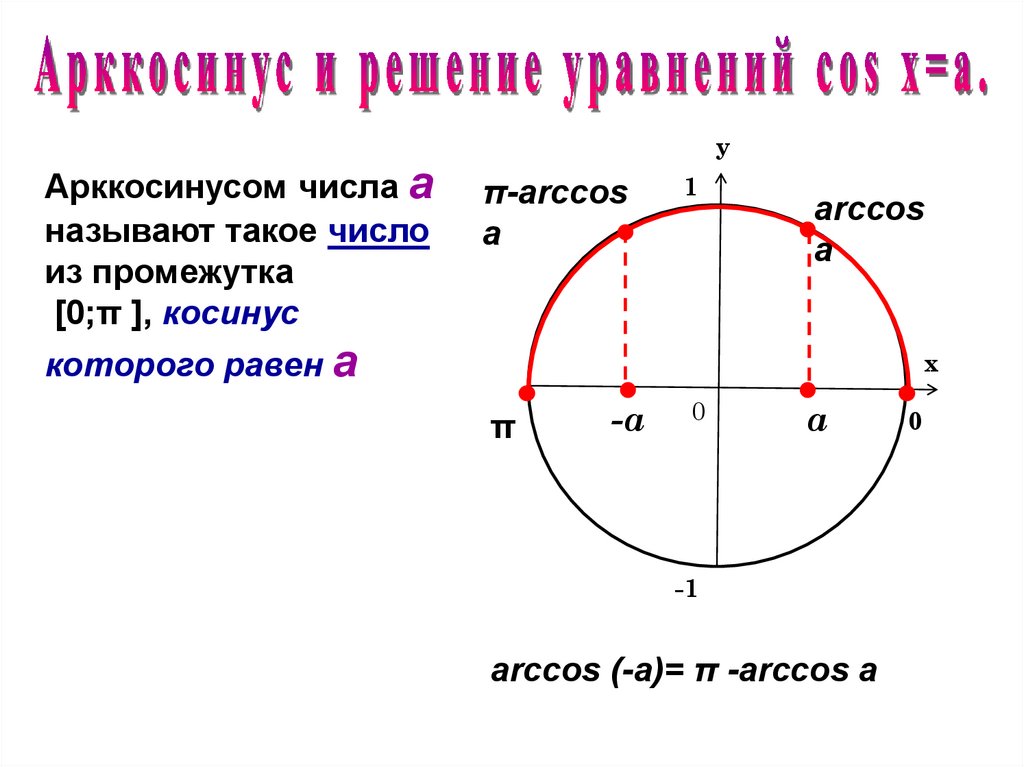
10.

Арккосинусом числа а
называют такое число
из промежутка
[0;π ], косинус
у
π-arccos
a
1
arccos
а
которого равен а
х
π
-а
0
а
-1
arccos (-a)= π -arccos a
0

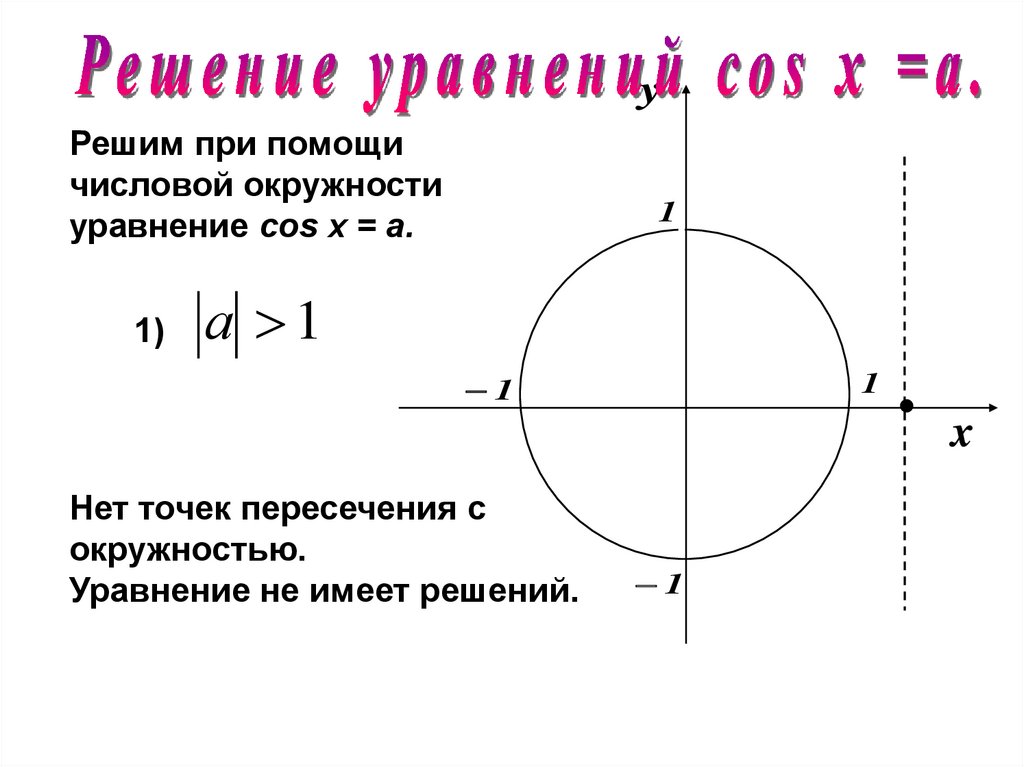
11.

y
Решим при помощи
числовой окружности
уравнение cos х = a.
1)
1
а 1
1
1
x
Нет точек пересечения с
окружностью.
Уравнение не имеет решений.
1

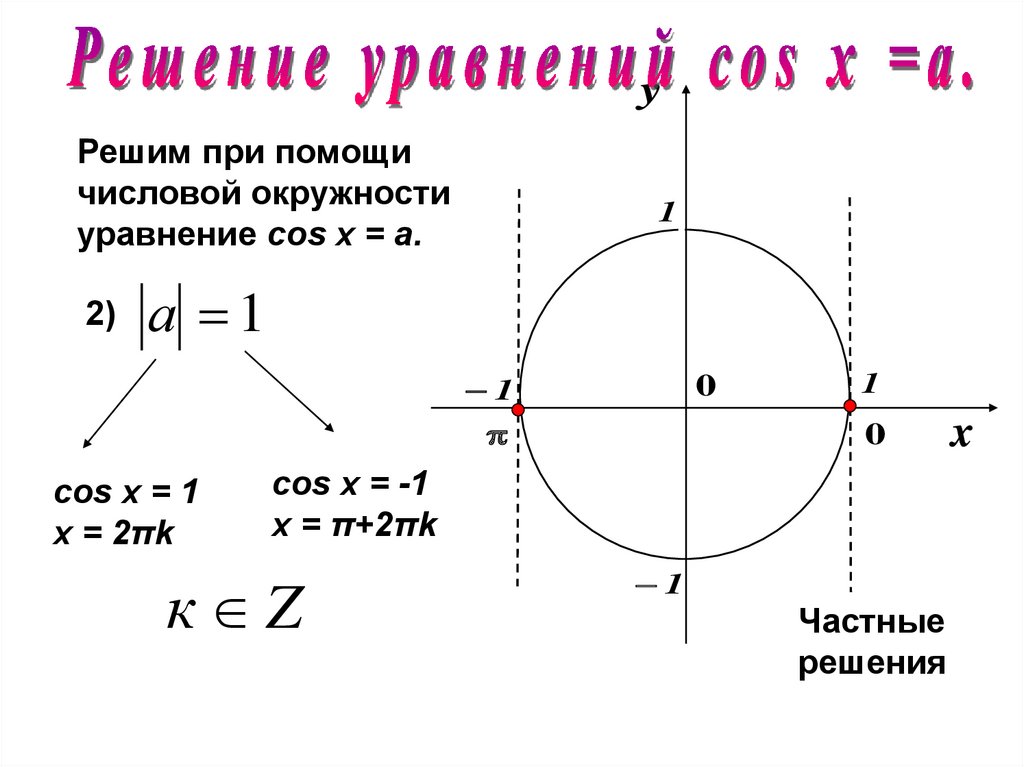
12.

y
Решим при помощи
числовой окружности
уравнение cos х = a.
2)
1
а 1
1
0
cos х = 1
х = 2πk
1
0
cos х = -1
х = π+2πk
к Z
1
Частные
решения
x

13.

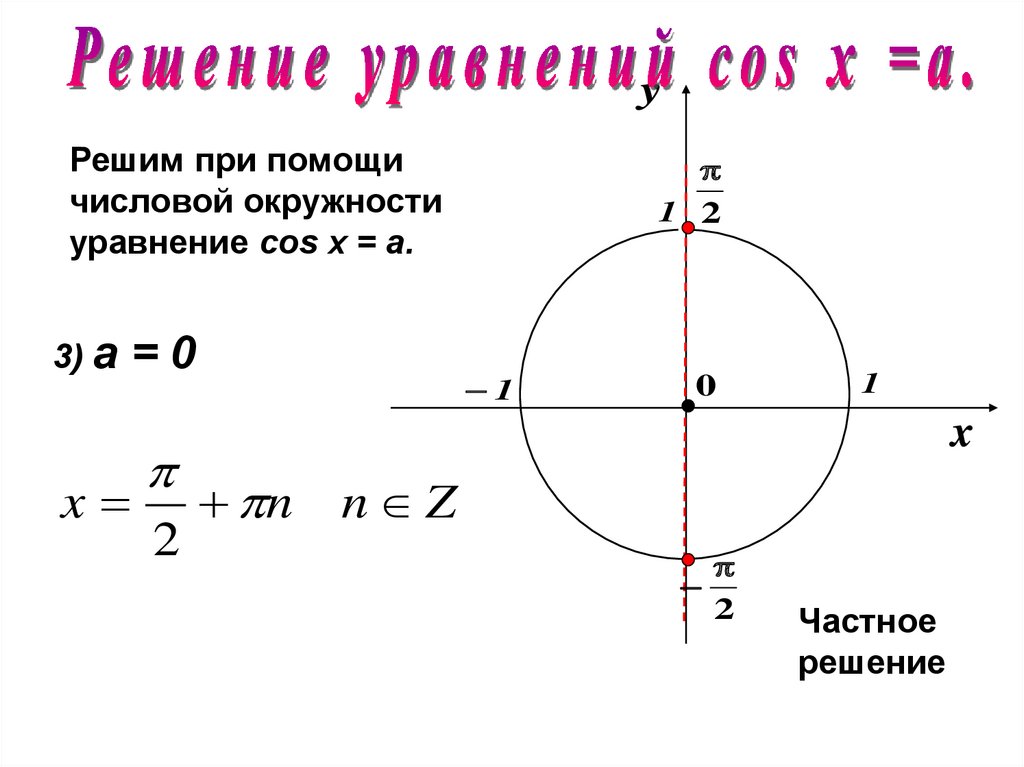
y
Решим при помощи
числовой окружности
уравнение cos х = a.
3) а
x
=0
2
1 2
1
0
1
x
n n Z
2
Частное
решение

14.

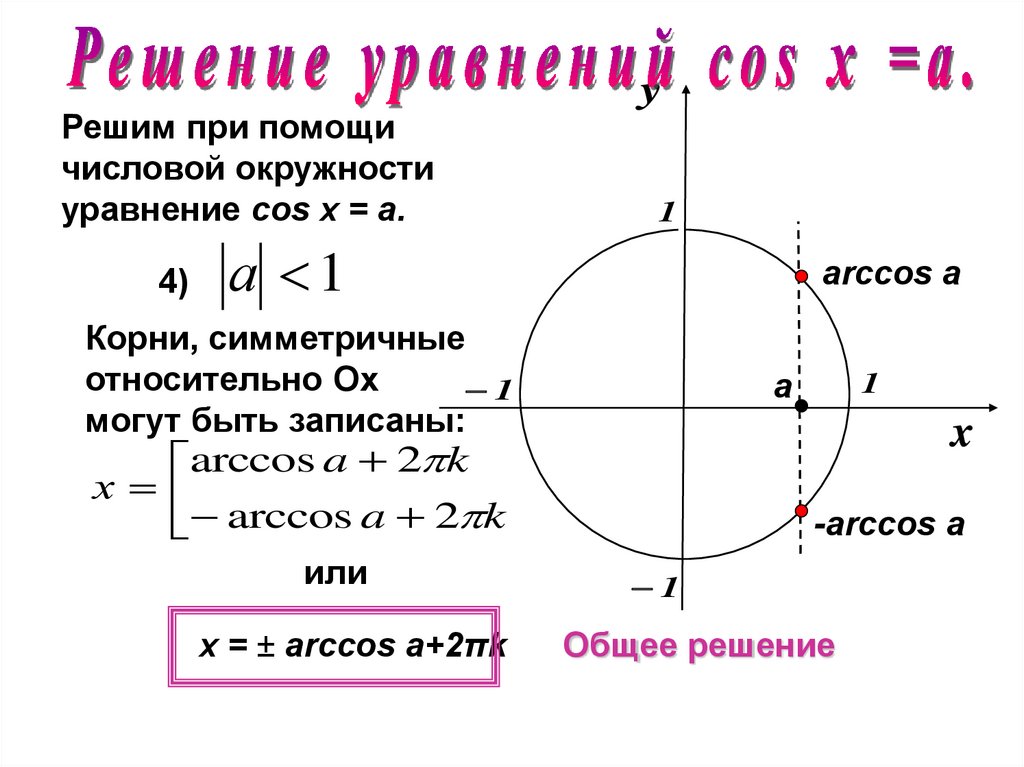
Решим при помощи
числовой окружности
уравнение cos х = a.
4)
y
1
а 1
arccos а
Корни, симметричные
относительно Оx
1
могут быть записаны:
а
x
arccos a 2 k
х
arccos a 2 k
или
х = ± arccos a+2πk
1
-arccos а
1
Общее решение

15.

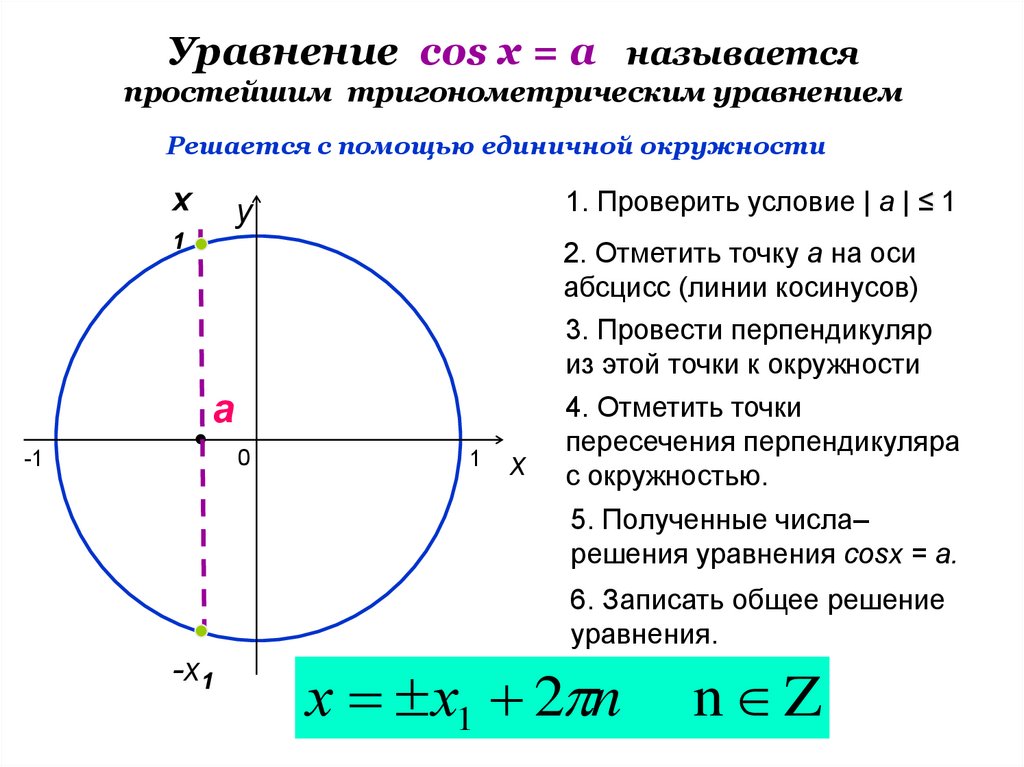
Уравнение cos х = a называется
простейшим тригонометрическим уравнением
Решается с помощью единичной окружности
х
1. Проверить условие | a | ≤ 1
y
1
a
0
-1
1
x
2. Отметить точку а на оси
абсцисс (линии косинусов)
3. Провести перпендикуляр
из этой точки к окружности
4. Отметить точки
пересечения перпендикуляра
с окружностью.
5. Полученные числа–
решения уравнения cosх = a.
6. Записать общее решение
уравнения.
-х1
х х1 2 n
n Z

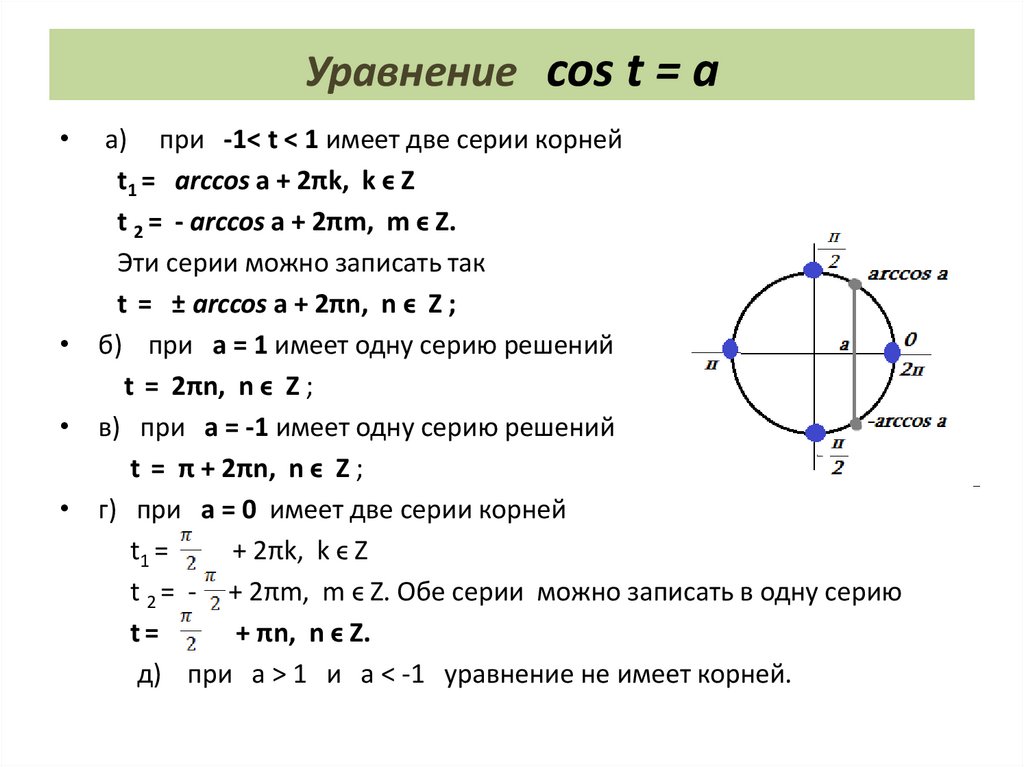
16.

Уравнение cos t = a
a) при -1< t < 1 имеет две серии корней
t1 = arсcos a + 2πk, k ϵ Z
t 2 = - arсcos a + 2πm, m ϵ Z.
Эти серии можно записать так
t = ± arсcos a + 2πn, n ϵ Z ;
• б) при а = 1 имеет одну серию решений
t = 2πn, n ϵ Z ;
• в) при а = -1 имеет одну серию решений
t = π + 2πn, n ϵ Z ;
• г) при а = 0 имеет две серии корней
t1 =
+ 2πk, k ϵ Z
t 2 = - + 2πm, m ϵ Z. Обе серии можно записать в одну серию
t=
+ πn, n ϵ Z.
д) при а > 1 и a < -1 уравнение не имеет корней.

17.

Решите уравнение
1) cos х =
1
2
2) cos х = -
1
2

18.

Решите уравнение
3) cos 4x = 1
4x = 2πn, n ϵ Z
4)

19.

.
Решите уравнение
5)

20.

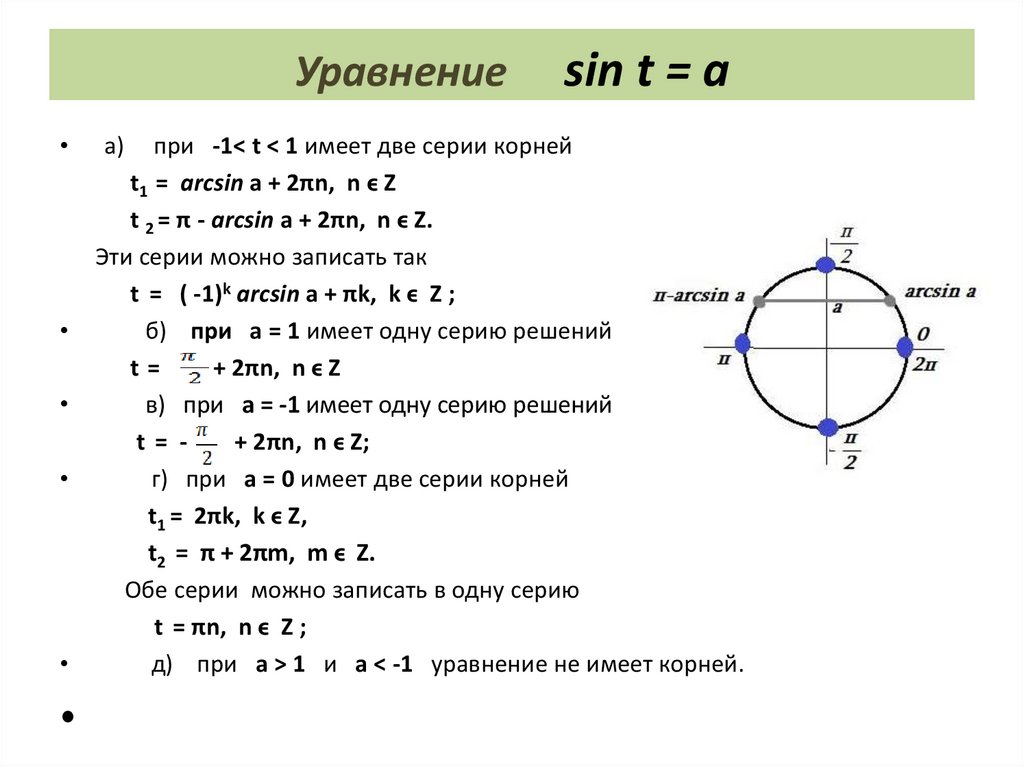
Уравнение
a)
sin t = a
при -1< t < 1 имеет две серии корней
t1 = arсsin a + 2πn, n ϵ Z
t 2 = π - arсsin a + 2πn, n ϵ Z.
Эти серии можно записать так
t = ( -1)k arсsin a + πk, k ϵ Z ;
б) при а = 1 имеет одну серию решений
t=
+ 2πn, n ϵ Z
в) при а = -1 имеет одну серию решений
t= + 2πn, n ϵ Z;
г) при а = 0 имеет две серии корней
t1 = 2πk, k ϵ Z,
t2 = π + 2πm, m ϵ Z.
Обе серии можно записать в одну серию
t = πn, n ϵ Z ;
д) при а > 1 и a < -1 уравнение не имеет корней.

21.

Решите уравнение
,,
1) sin х =
x = ( -1)k
+ πk,
kϵ Z.

22.

(;
Решите
,,;
2) sin х = -
x = ( -1)k ( -
уравнение
2
2
+ πk, k ϵ Z
x = ( -1)k+1
+ πk, k ϵ Z

23.

Задание 2. Найти корни уравнения:
1) a) sin x =1 б) sin x = - 1 в) sin x = 0
г) sin x =1,2
д) sin x = 0,7
2) а)
б)
в)
г)

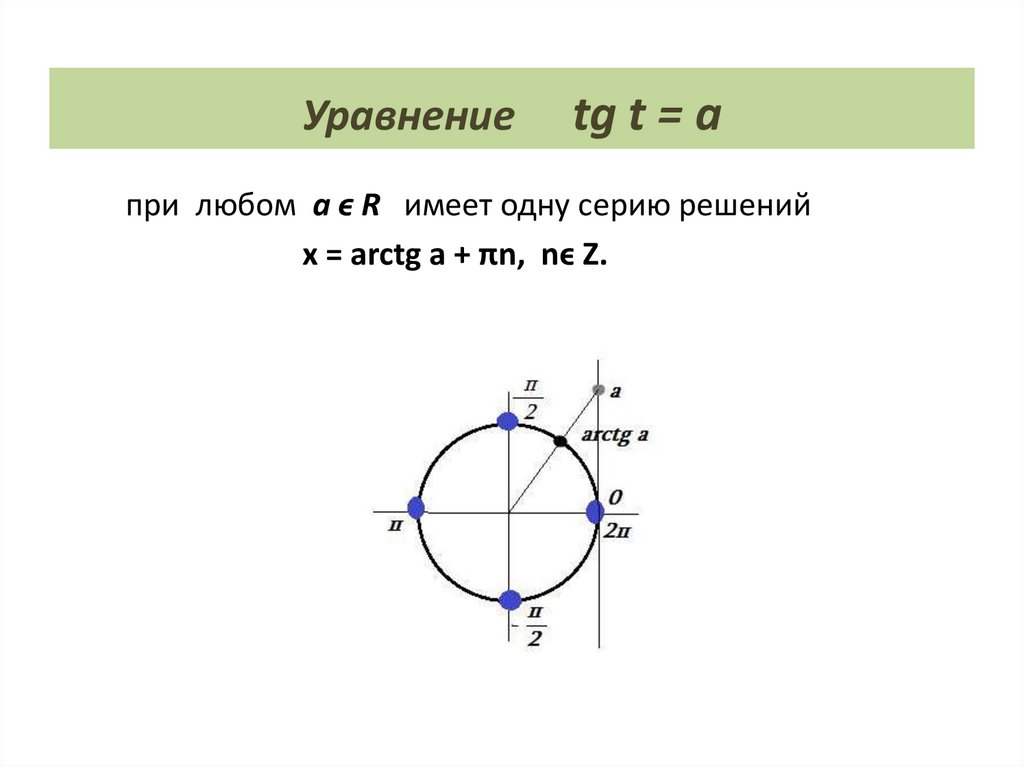
24.

Уравнение
tg t = a
при любом а ϵ R имеет одну серию решений
х = аrctg a + πn, nϵ Z.

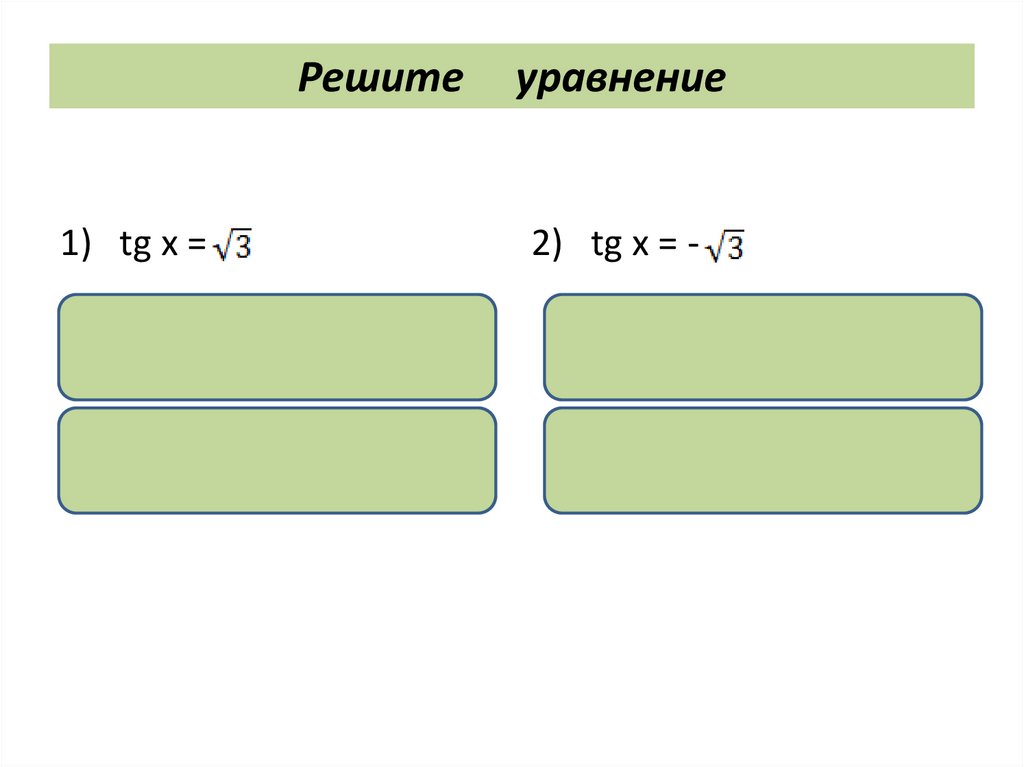
25.

Решите
1) tg x =
х = аrctg
x=
уравнение
2) tg x = -
+ πn, nϵ Z.
+ πn, nϵ Z.
х = аrctg(x=-
) + πn, nϵ Z,
+ πn, nϵ Z.

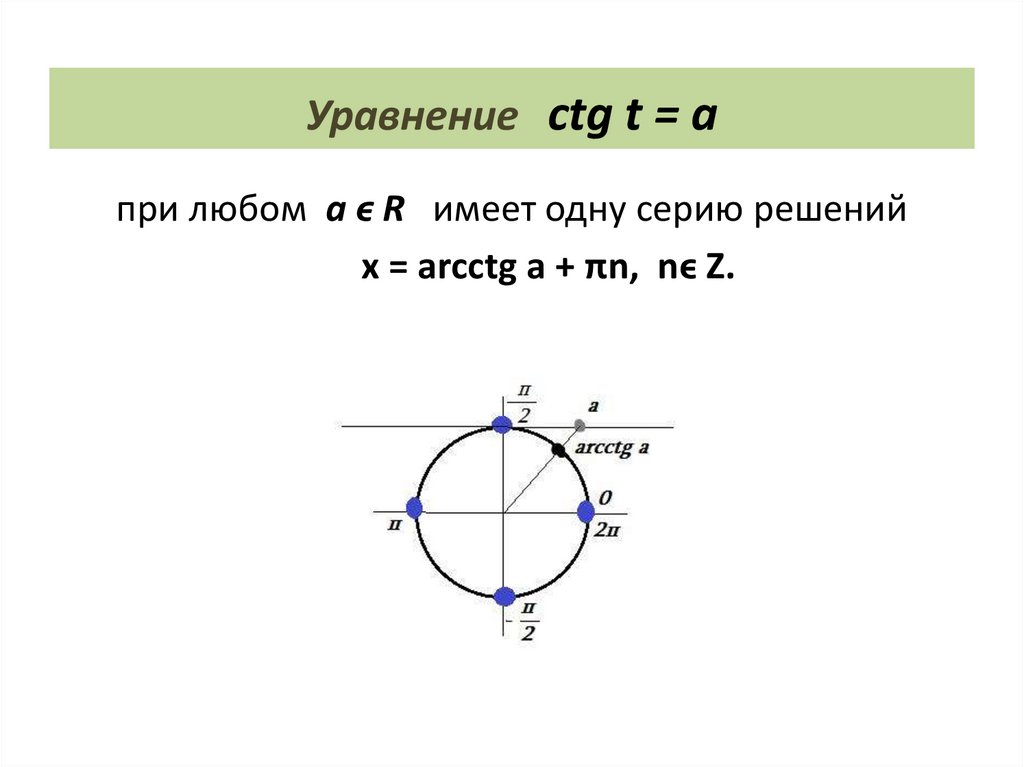
26.

Уравнение ctg t = a
при любом а ϵ R имеет одну серию решений
х = аrcctg a + πn, nϵ Z.

27.

Решите
1) ctg x = 1
уравнение
2)
ctg x = - 1
х = аrcctg 1 + πn, nϵ Z,
х = аrcctg ( -1) + πn, nϵ Z
х=
х = π - аrcctg 1 + πn, nϵ Z
+ πn, nϵ Z.
х=
+ πn, nϵ Z.

28.

Подводим итоги