Функции и их свойства

1.

Тема: «Функция и её свойства»
Подготовила: студентка группы ПС-16
Оплетаева Александра

2.

Определение функции
Функция
–
это
соответствие
между
множествами X и Y, где каждому элементу из
множества X соответствует один элемент из
множества Y.
Способы задания функции:
1. аналитический;
2. графический;
3. с помощью графов.

3.

Свойства функций
Область определения функции – множество
значений независимой переменной X, для
которых функции определена.
1.
Найти область определения (D:)
а) y
x 3
x-3 ≥ 0
D: x ≥ 3
5x
б) y
4-x
4-x ≠ 0
x≠4
D: x ∈ (-∞;4) v (4;+∞)
x ∈ R, x ≠ 4

4.

Свойства функций
в). D: x ∈ R
г). D: -2 ≤ x ≤ 3

5.

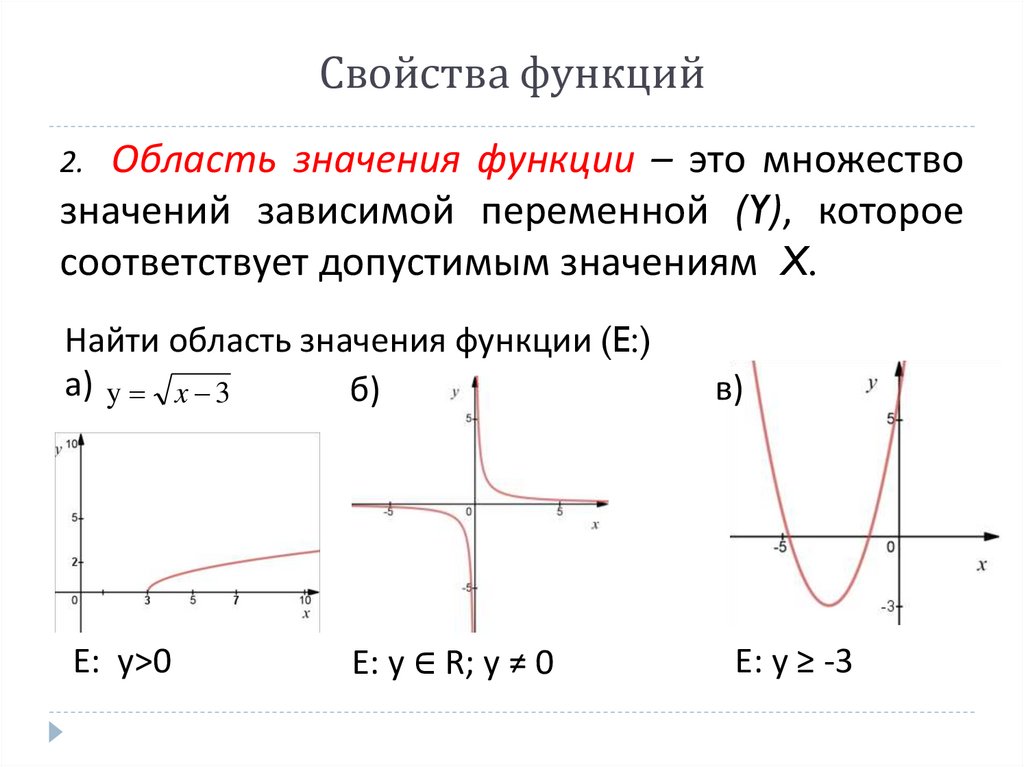
Свойства функций
Область значения функции – это множество
значений зависимой переменной (Y), которое
соответствует допустимым значениям X.
2.
Найти область значения функции (E:)
a) y x 3
б)
E: y>0
E: y ∈ R; y ≠ 0
в)
E: y ≥ -3

6.

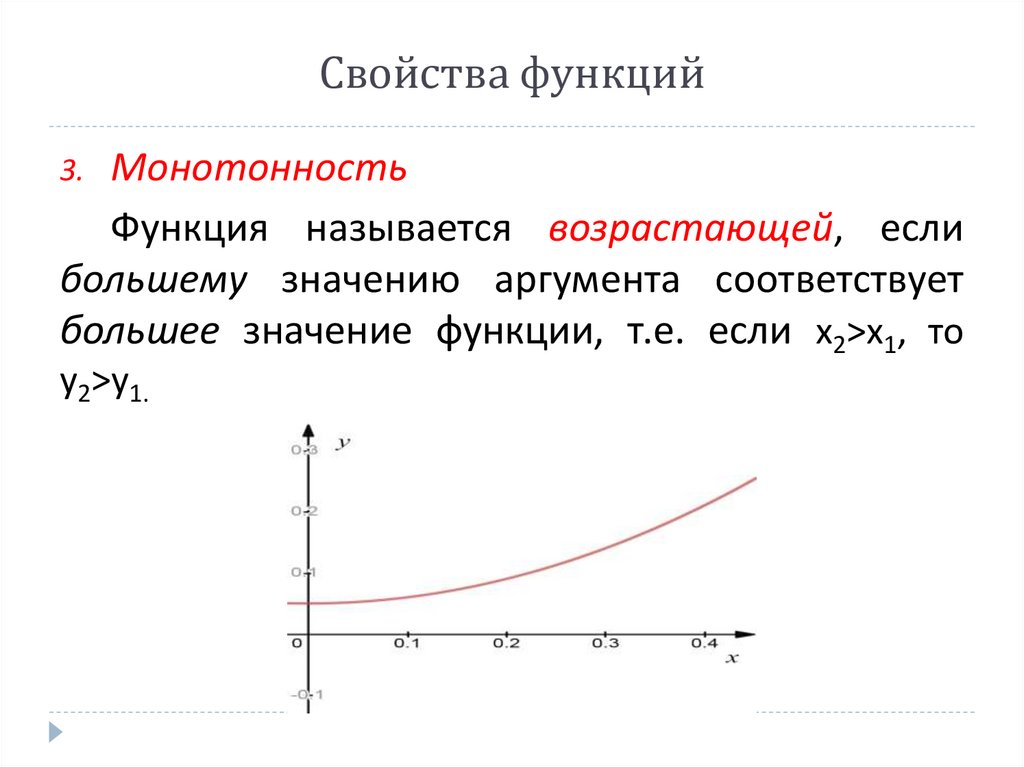
Свойства функций
Монотонность
Функция называется возрастающей, если
большему значению аргумента соответствует
большее значение функции, т.е. если x2>x1, то
3.
y2>y1.

7.

Свойства функций
Функция называется убывающей, если
большему значению аргумента соответствует
меньшее значение функции, т.е. если x2>x1, то
y2<y1.

8.

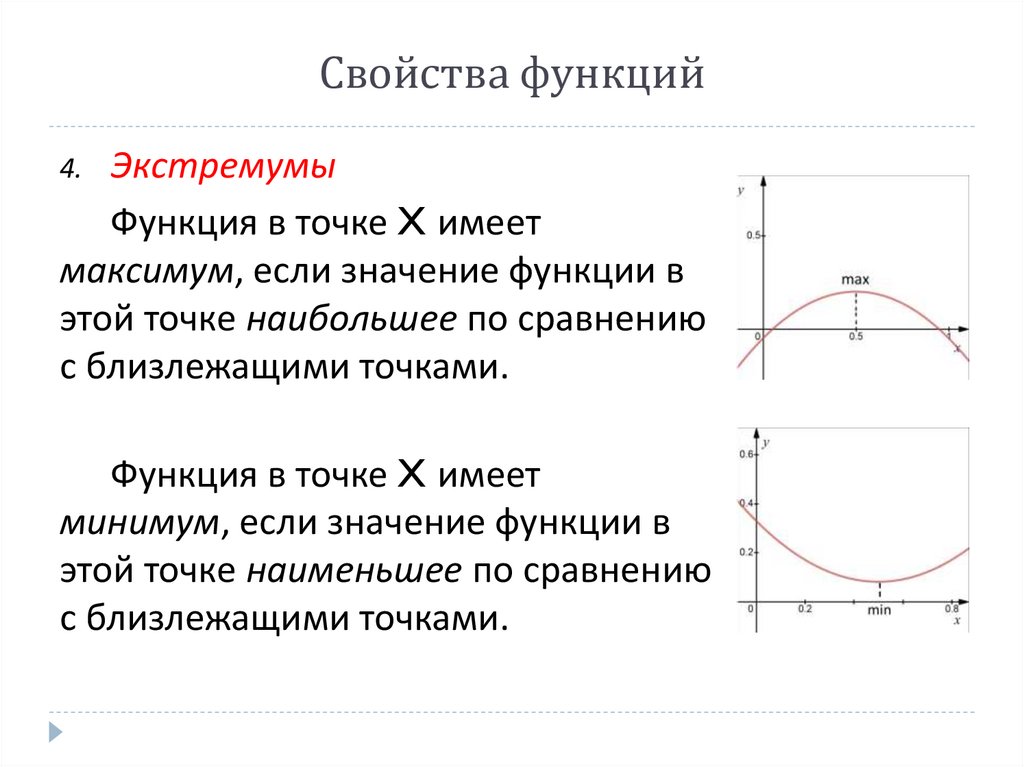
Свойства функций
Экстремумы
Функция в точке X имеет
максимум, если значение функции в
этой точке наибольшее по сравнению
с близлежащими точками.
4.
Функция в точке X имеет
минимум, если значение функции в
этой точке наименьшее по сравнению
с близлежащими точками.

9.

Свойства функции
Функция чётная, если с
изменением знака аргумента знак
функции не меняется, т.е. ƒ(-X)= ƒ(X).
График чётной функции
симметричен относительно оси OY.
Функция нечётная, если с
изменением знака аргумента знак
функции меняется, т.е. ƒ(-X)=- ƒ(X).
График нечётной функции
симметричен относительно начала
координат.

10.

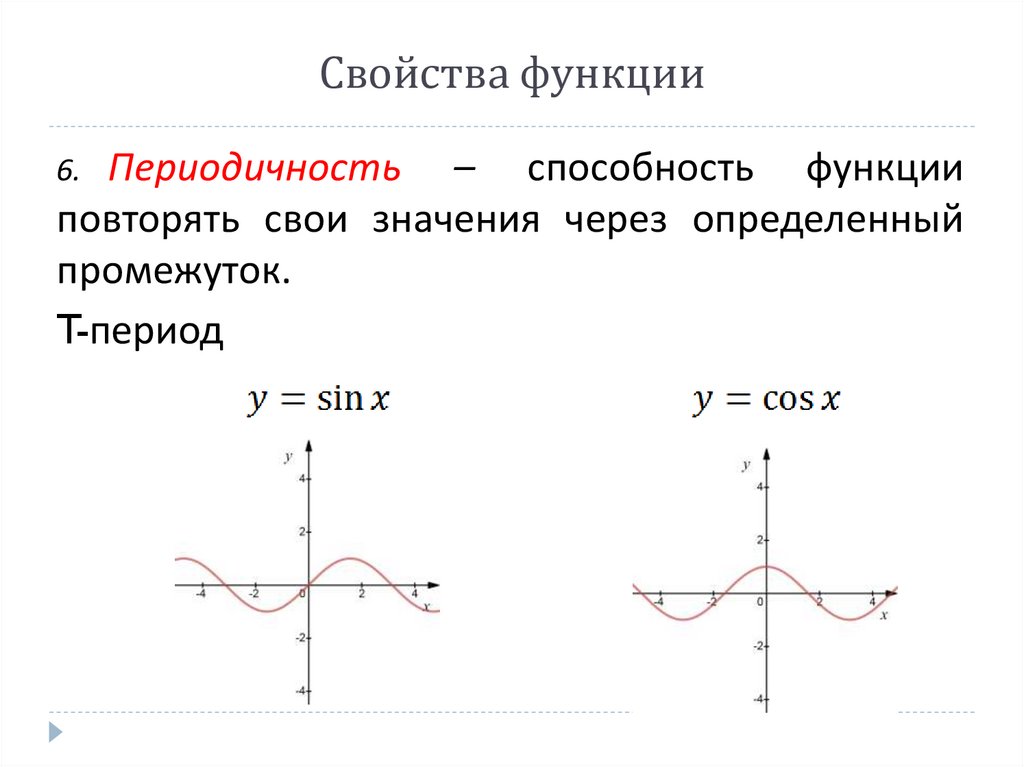
Свойства функции
Периодичность – способность функции
повторять свои значения через определенный
промежуток.
T-период
6.

11.

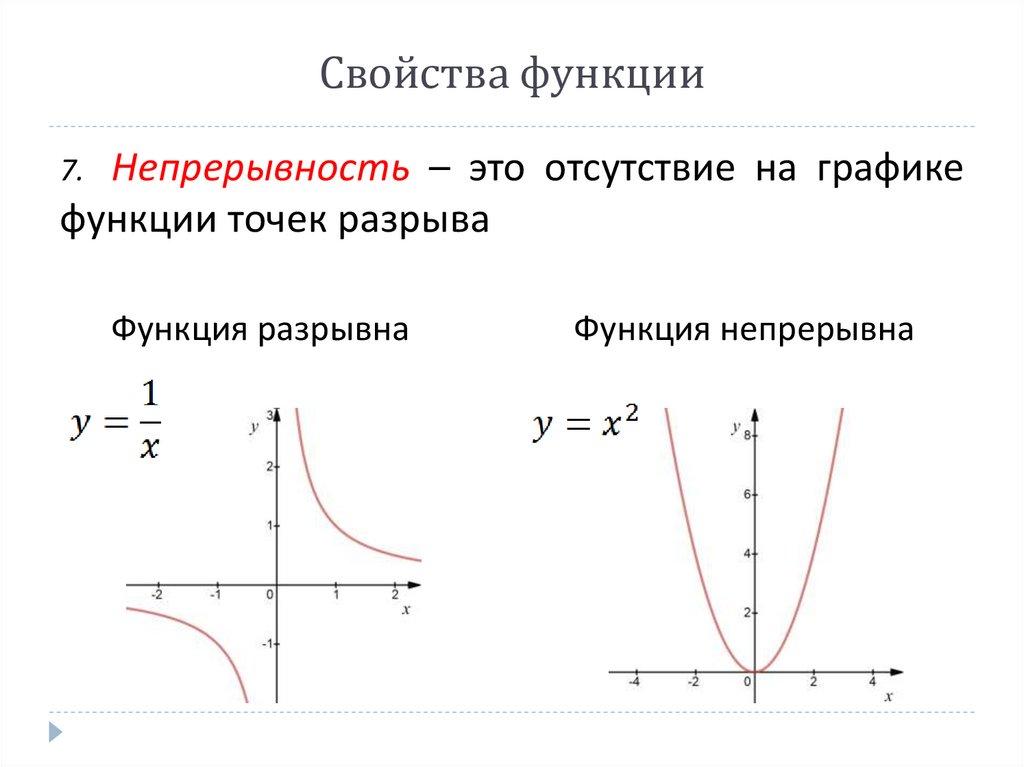
Свойства функции
Непрерывность – это отсутствие на графике
функции точек разрыва
7.
Функция разрывна
Функция непрерывна

12.

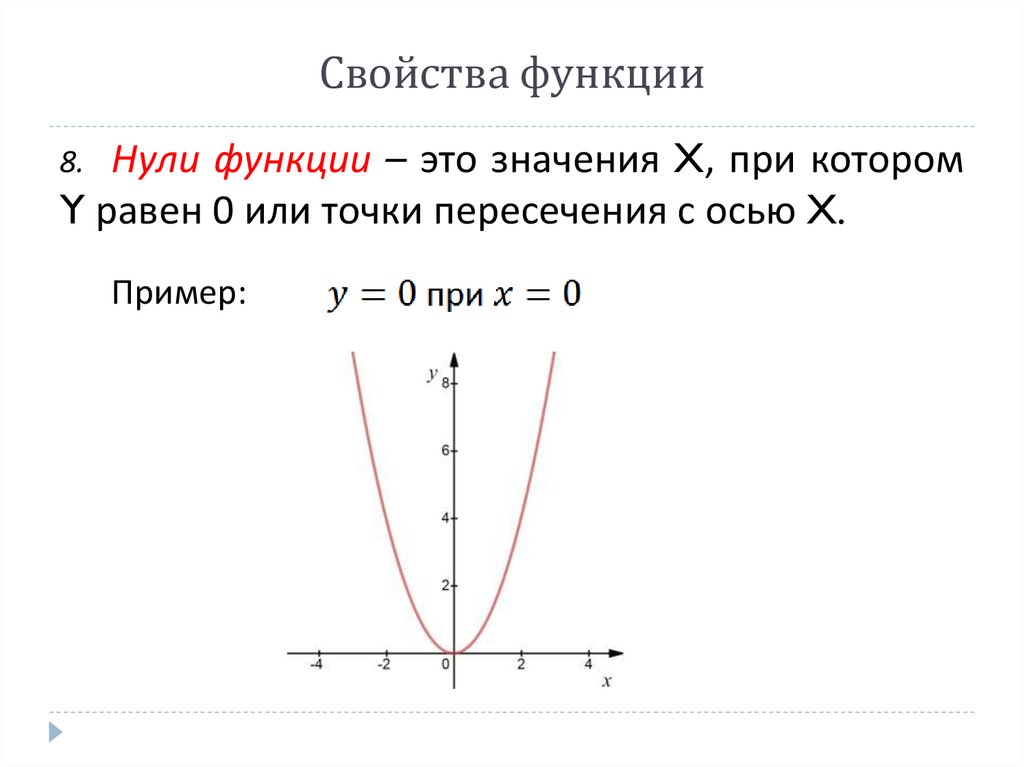
Свойства функции
Нули функции – это значения X, при котором
Y равен 0 или точки пересечения с осью X.
8.
Пример:

13.

Свойства функций
5. Построить функцию и написать её свойства.
y x2 4x
y x 1
1). D: x ∈ R
1). D: x ≥ -1
2). E: y ≥ -4
2). E: y > 0
3). ↑ x ≥ -2
↓ x ≤ -2
3). ↑ x ≥ -1
4). min (-2;-4)
4). min (-1;0)
5). функция общего вида
5). функция общего вида
6). непериодичная
6). непериодичная
7). непрерывная
7). непрерывная
8). y=0 при x=0, x=-4
8). y=0 при x=-1

14.

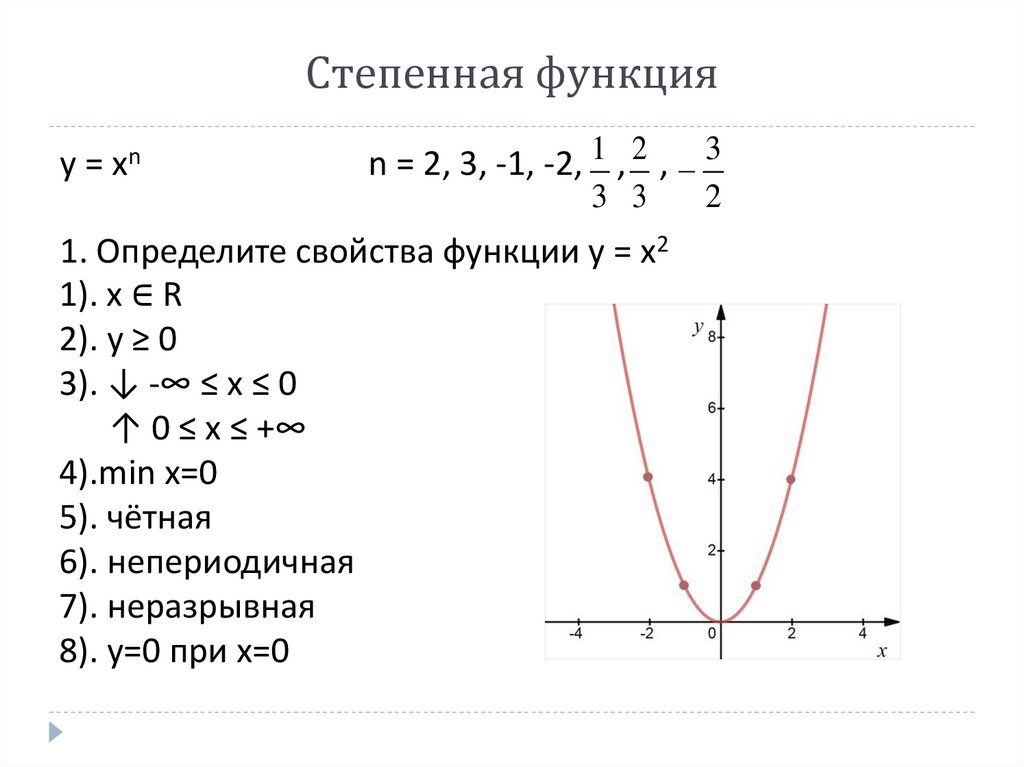
Степенная функция
y = xn
n = 2, 3, -1, -2, 1 , 2 , 3
3 3
1. Определите свойства функции y = x2
1). x ∈ R
2). y ≥ 0
3). ↓ -∞ ≤ x ≤ 0
↑ 0 ≤ x ≤ +∞
4).min x=0
5). чётная
6). непериодичная
7). неразрывная
8). y=0 при x=0
2

15.

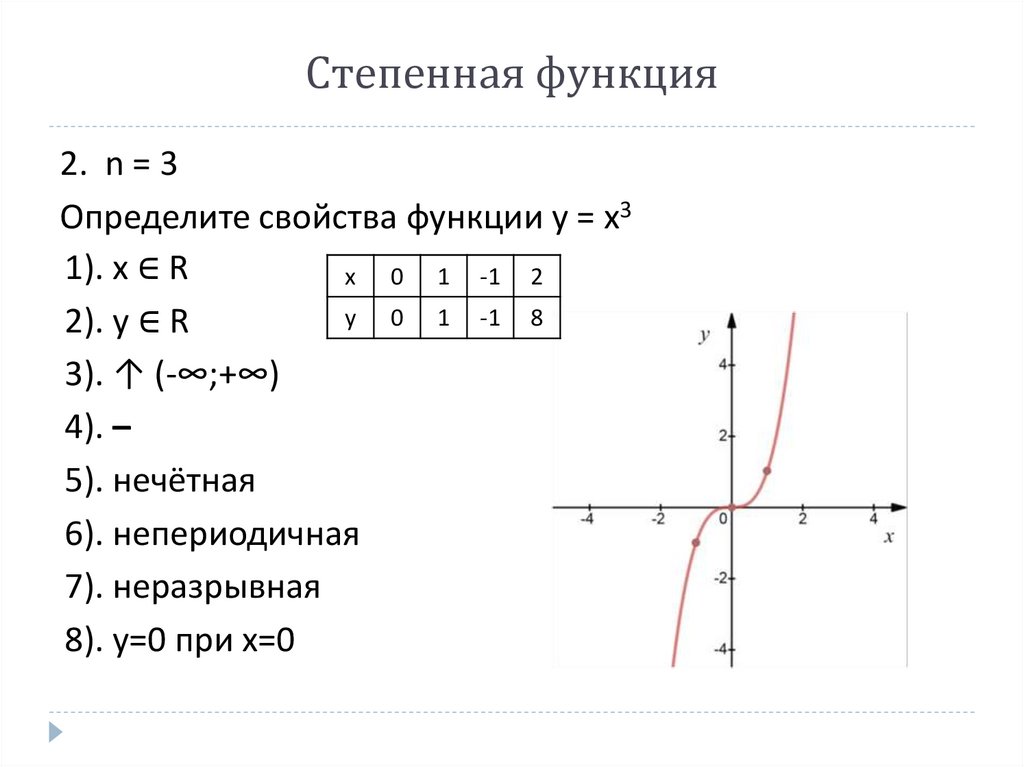
Степенная функция
2. n = 3
Определите свойства функции y = x3
1). x ∈ R
x 0 1 -1 2
y 0 1 -1 8
2). y ∈ R
3). ↑ (-∞;+∞)
4). –
5). нечётная
6). непериодичная
7). неразрывная
8). y=0 при x=0

16.

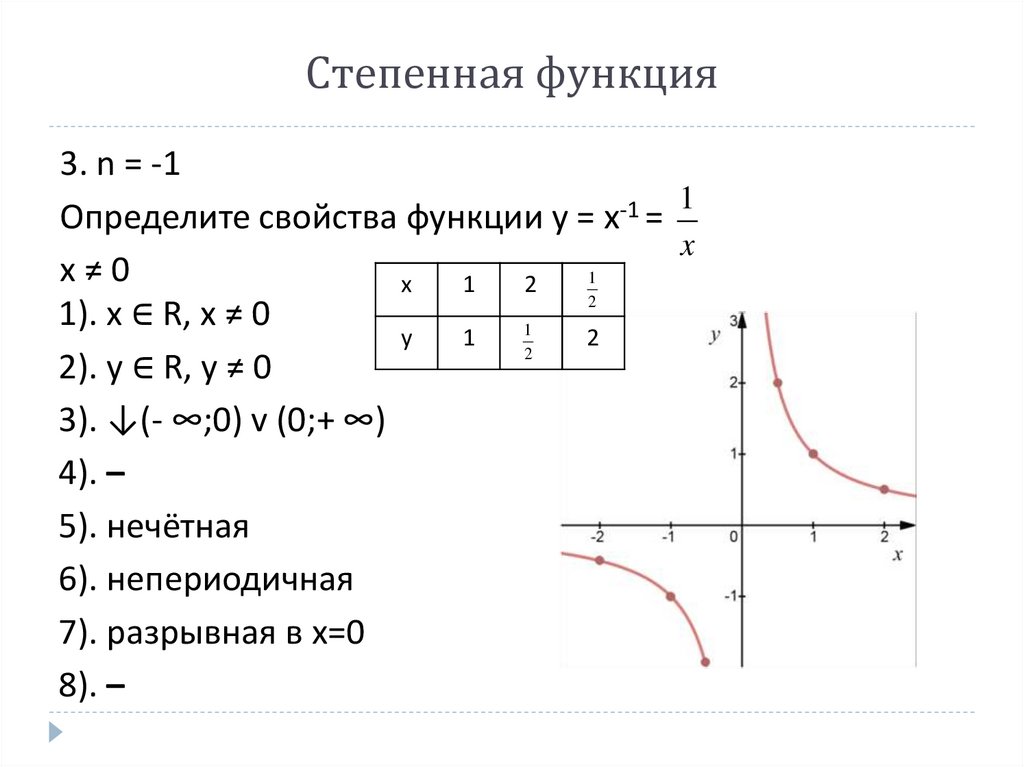
Степенная функция
3. n = -1
1
-1
Определите свойства функции y = x =
x
x≠0
1
x
1
2
2
1). x ∈ R, x ≠ 0
1
y
1
2
2
2). y ∈ R, y ≠ 0
3). ↓(- ∞;0) v (0;+ ∞)
4). –
5). нечётная
6). непериодичная
7). разрывная в x=0
8). –

17.

Степенная функция
4. n = -2
Определите свойства функции y = x-2 =
1). x ∈ R, x ≠ 0
1
x
1
-1
2
2
1
2). y>0
y
1
1
4
4
3). ↑(- ∞;0)
↓ (0;+ ∞)
4). 5). чётная
6). непериодичная
7). разрывная в x=0
8). -
x≠0;y≠0

18.

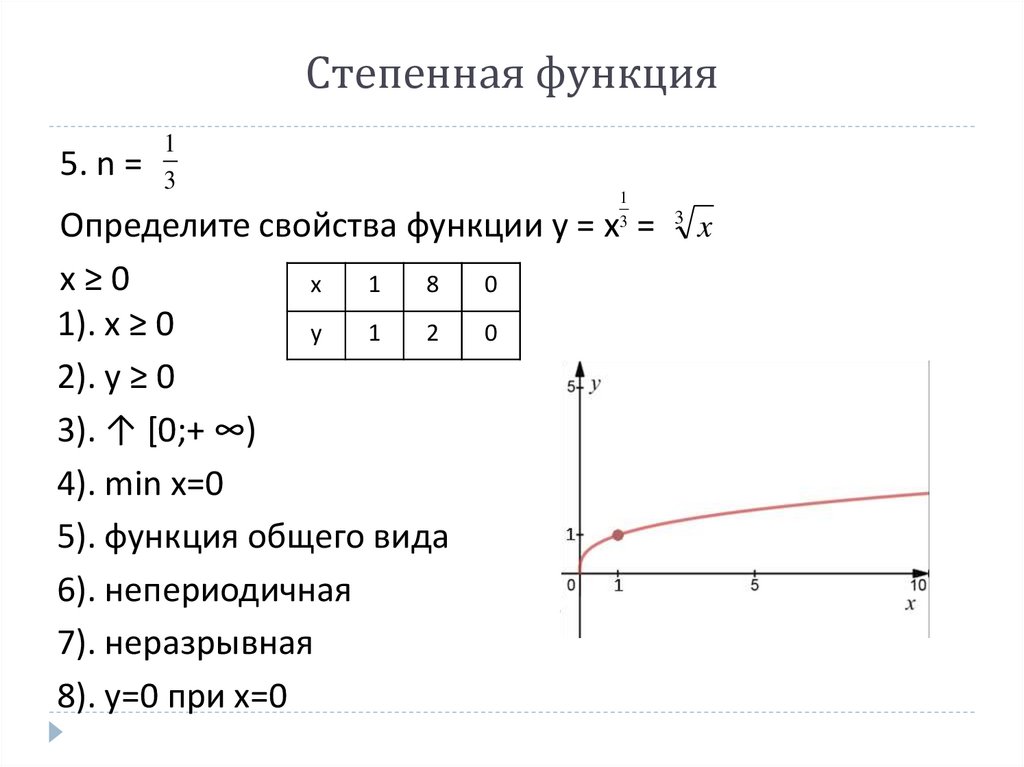
Степенная функция
5. n =
1
3
1
3
Определите свойства функции y = x =
x≥0
x
1
8
0
1). x ≥ 0
y
1
2
0
2). y ≥ 0
3). ↑ [0;+ ∞)
4). min x=0
5). функция общего вида
6). непериодичная
7). неразрывная
8). y=0 при x=0
3
x

19.

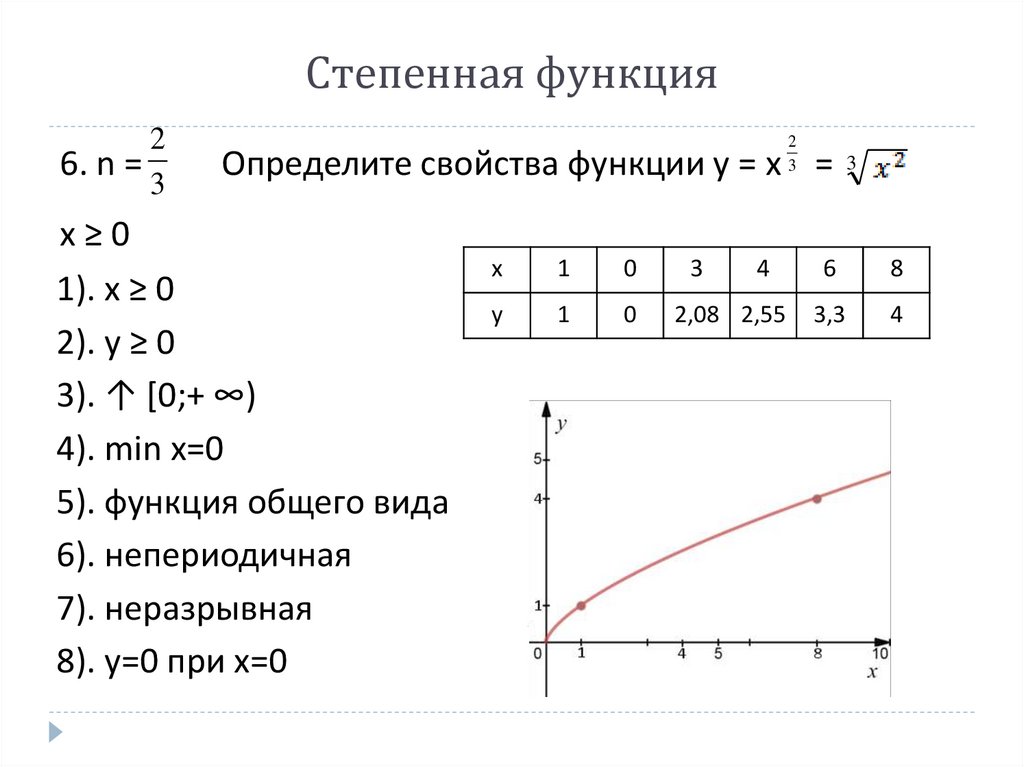
Степенная функция
2
6. n =
3
2
3
Определите свойства функции y = x =
x≥0
1). x ≥ 0
2). y ≥ 0
3). ↑ [0;+ ∞)
4). min x=0
5). функция общего вида
6). непериодичная
7). неразрывная
8). y=0 при x=0
x
1
0
y
1
0
3
4
2,08 2,55
3
6
8
3,3
4

20.

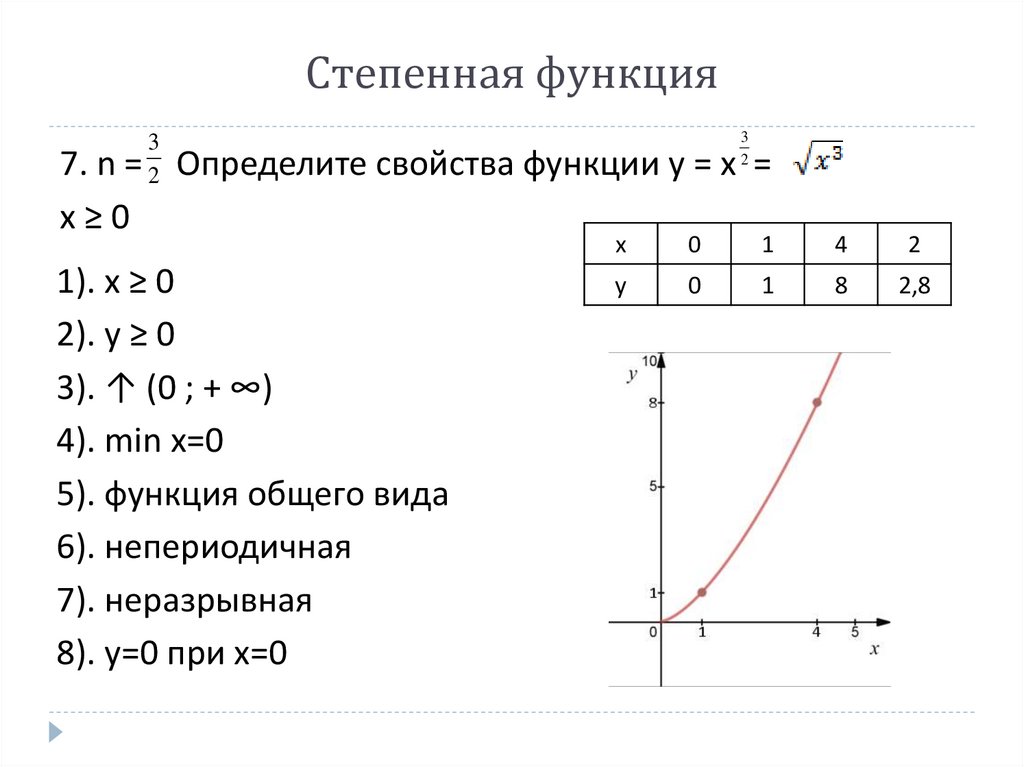
Степенная функция
3
=2
7. n
x≥0
3
2
Определите свойства функции y = x =
1). x ≥ 0
2). y ≥ 0
3). ↑ (0 ; + ∞)
4). min x=0
5). функция общего вида
6). непериодичная
7). неразрывная
8). y=0 при x=0
x
0
1
4
2
y
0
1
8
2,8

21.

Спасибо за внимание!