Механические волны

1.

МЕХАНИЧЕСКИЕ
ВОЛНЫ

2.

Механические волны
Колеблющиеся тело, помещенное в упругую среду,
является источником колебаний, распространяющихся от
него во все стороны.
Процесс распространения колебаний в пространстве
называется волной

3.

При распространении волны, частицы среды не
движутся вместе с волной, а колеблются около своих
положений равновесия.
Вместе с волной от частицы к частице, передается
лишь состояние колебательного движения и его энергия.
Основным свойством всех волн независимо от их
природы является перенос энергии без переноса
вещества.

4.

Волны бывают поперечными (колебания происходят в
плоскости,
перпендикулярной
направлению
распространения), и продольными (сгущение и
разряжение частиц среды происходят в направлении
распространения).

5.

Механической волной называют механические
возмущения, распространяющиеся в пространстве
и несущие энергию.
Продольная волна – это волна, в которой частицы
среды колеблются вдоль направления распространения
волны.
Поперечная волна - это волна, в которой частицы
среды колеблются в направлениях, перпендикулярных к
направлению распространения волны.

6.

Если взаимосвязь между частицами среды осуществляется
силами
упругости,
возникающими
вследствие
деформации среды при передаче колебаний от одних
частиц к другим, то волны называются упругими
(звуковые, ультразвуковые, сейсмические и др. волны).
Упругие поперечные волны возникают в среде,
обладающей сопротивлением сдвигу,
вследствие этого:
в жидкой и газообразной средах возможно
возникновение только продольных волн;
в твердой среде возможно возникновение как
продольных, так и поперечных волн.

7.

Волновая функция
( x, y , z , t )
Расстояние между ближайшими частицами,
колеблющимися в одинаковой фазе, называется длиной
волны :
T
– частота
T
1
– скорость распространения волны :
– период

8.

Фронт волны – геометрическое место точек, до которых
доходит возмущение в момент времени t.
В однородной среде направление распространения
перпендикулярно фронту волны .
Волновая поверхность – геометрическое место точек,
колеблющихся в одинаковой фазе.
Число волновых поверхностей – бесконечно.
Фронт волны – один.
Волновые поверхности неподвижны.
Фронт волны все время перемещается

9.

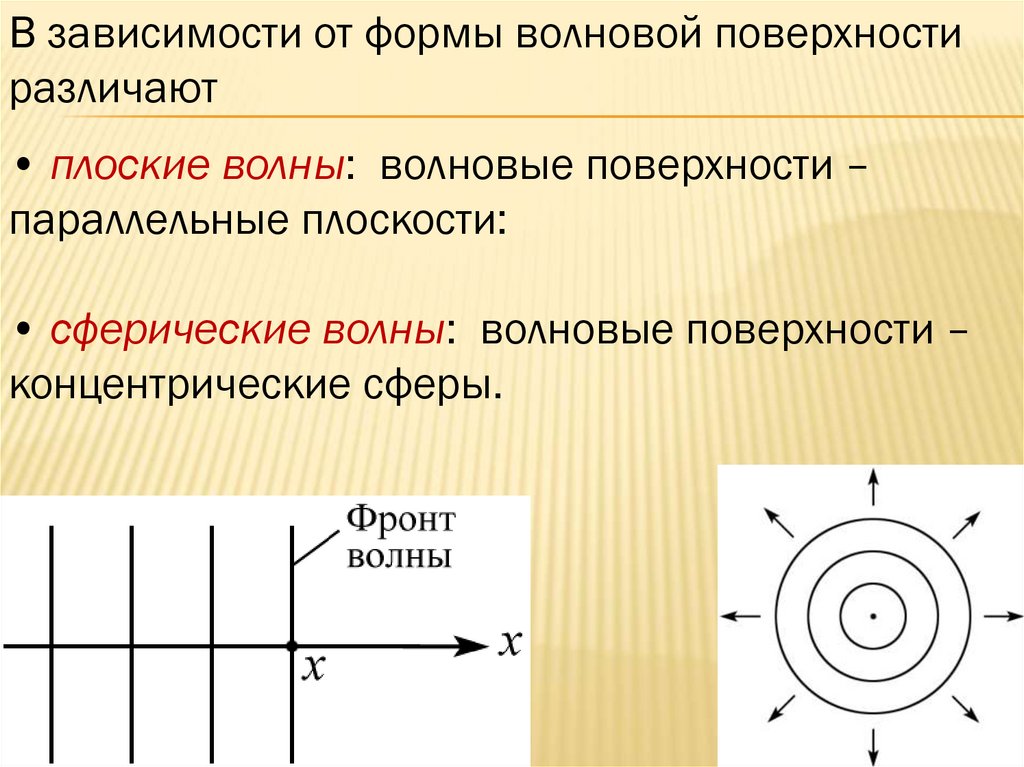
В зависимости от формы волновой поверхности
различают
• плоские волны: волновые поверхности –
параллельные плоскости:
• сферические волны: волновые поверхности –
концентрические сферы.

10.

Уравнение плоской и сферической волны. Волновое
уравнение.
Уравнением волны – называется выражение,
которое дает смещение колеблющейся точки как
функцию ее координат (x, y, z) и времени t.
f ( x, y , z , t ) ( x, y , z , t )

11.

Уравнение плоской волны
Найдем вид волновой функции, в случае плоской волны предполагая, что
колебания носят гармонический характер:
A cos( t 0 )
Пусть
0 0
(0, t ) A cos t
Чтобы пройти путь x необходимо время
x
x
( x, t ) A cos t
– это уравнение плоской волны.

12.

Введем волновое число
k
2
или в векторной форме
Так как
T , то
Отсюда
2
k
n
2 2
k
T
k
Тогда уравнение плоской волны запишется так:
A cos( t kx)

13.

A cos( t kx 0 )
При поглощении средой энергии волны:
Ae
t
cos( t kx 0 )
-наблюдается
затухание
волны
(уменьшение
интенсивности волны по мере удаления от источника
колебаний);
β – коэффициент затухания;
А – амплитуда.

14.

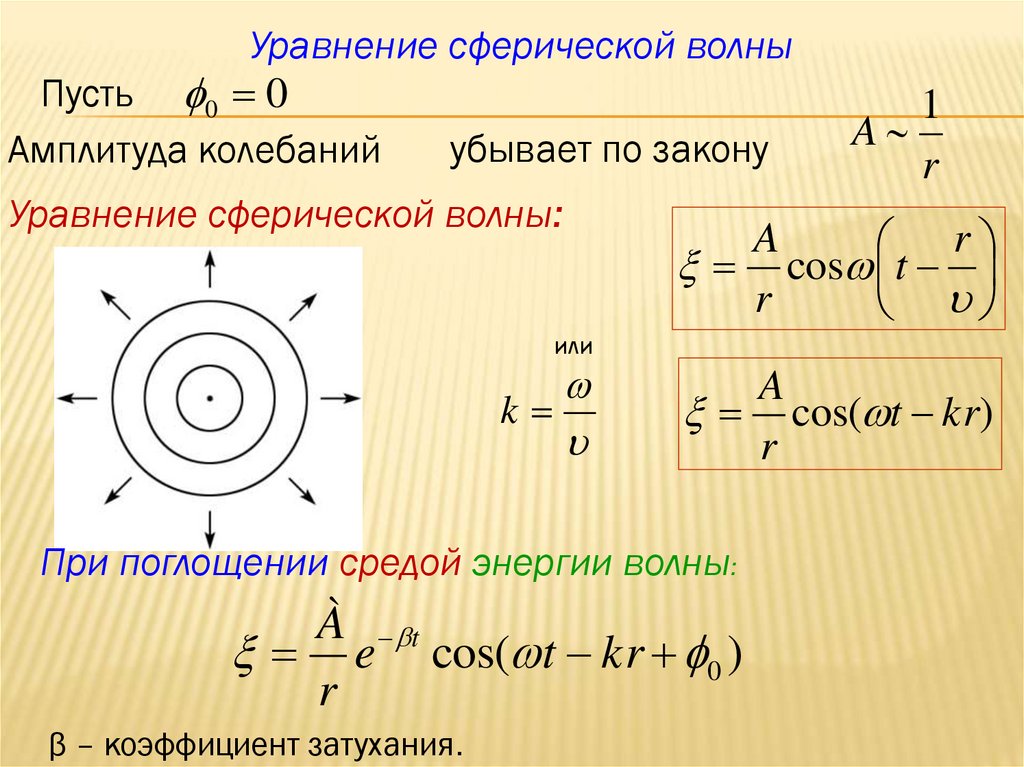
Уравнение сферической волны
Пусть 0 0
Амплитуда колебаний
убывает по закону
Уравнение сферической волны:
1
A
r
A
r
cos t
r
или
k
A
cos( t kr)
r
При поглощении средой энергии волны:
À t
e cos( t kr 0 )
r
β – коэффициент затухания.

15.

Распространение волн в однородной среде в общем
случае описывается волновым уравнением –
дифференциальным уравнением в частных производных:
1
2 2 2 2
2
x
y
z
t
2
2
2
2
1
2 2
t
2
2
Любая функция, удовлетворяющая этому уравнению,
описывает некоторую волну, причем -фазовая скорость
волны

16.

Решением волнового уравнения является уравнение
любой волны, например
сферической:
A
cos( t kr)
r
или плоской :
A cos( t kr)
Для плоской волны, распространяющейся вдоль оси x,
волновое уравнение упрощается:
1
2 2
2
x
t
2
оператор Лапласа:
2
2
2
2
2 2 2 2
x y z

17.

Фазовая скорость. Групповая скорость.
Фазовая скорость – это скорость распространения фазы
волны. (скорость распространения волны)
dx
dt
Для синусоидальной волны скорость переноса
энергии равна фазовой скорости.
Скорость волны (v) - это скорость распространения
колебаний в упругой среде. Скорость волны
равняется произведению длины волны на её
частоту.
v

18.

ПОТОК ЭНЕРГИИ ВОЛН
Волновой процесс связан с распределением энергии.
Количественной характеристикой перенесенной энергии
является поток энергии.
Поток энергии (Ф) – средняя энергия (т. е. за время,
значительно больше периода колебаний), переносимая
волнами в единицу времени через некоторую поверхность.
Единица измерения потока 1 ватт (Вт).
dW
Ф
dt
dW
j
dSdt