Similar presentations:
Уравнение с двумя переменными
1.
Уравнение с двумяпеременными
и его график
2.
Каждое из уравненийxy – 8 =0
является уравнением с двумя переменными.
3.
41
4.
Решением уравнения с двумя переменныминазывается пара значений переменных,
обращающая это уравнение в верное
равенство.
5.
Уравнение с двумя переменными обычноимеет бесконечное множество
решений.
Два уравнения, имеющие одно и то же
множество решений,
называют равносильными уравнениями.
6.
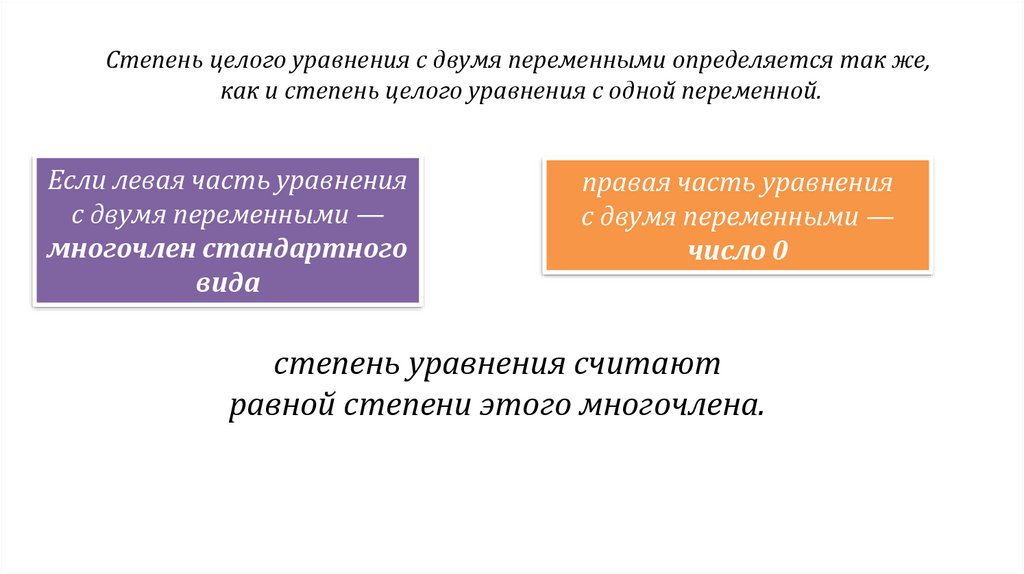
Степень целого уравнения с двумя переменными определяется так же,как и степень целого уравнения с одной переменной.
Если левая часть уравнения
с двумя переменными —
многочлен стандартного
вида
правая часть уравнения
с двумя переменными —
число 0
степень уравнения считают
равной степени этого многочлена.
7.
Чтобы выяснить степень уравнения с двумяпеременными, его заменяют равносильным
уравнением, левая часть которого —
многочлен стандартного вида,
а правая – число нуль.
8.
Уравнение третьей степени9.
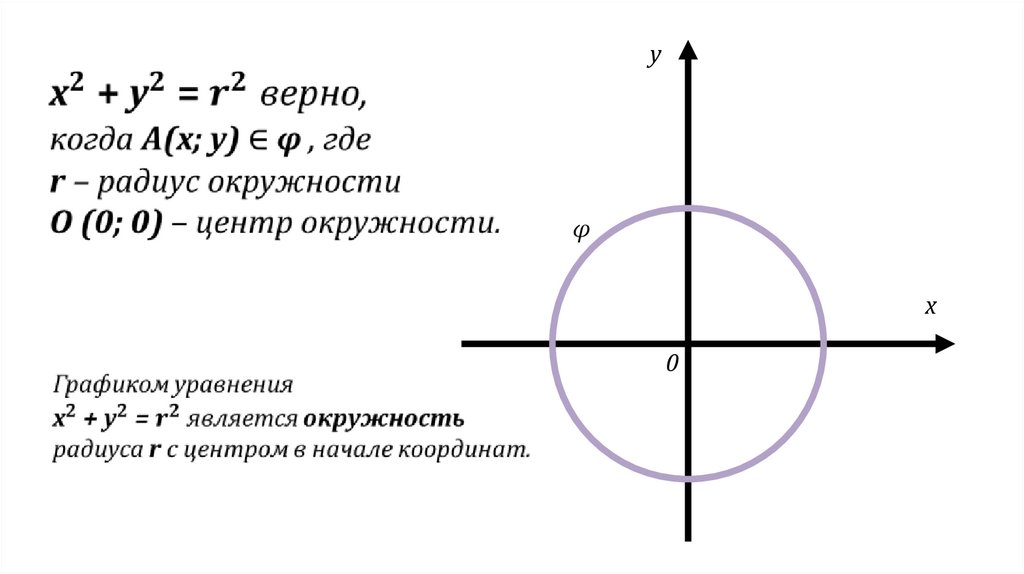
Графиком уравнения с двумя переменныминазывается множество точек координатной
плоскости, координаты которых обращают
уравнение в верное равенство.
10.
11.
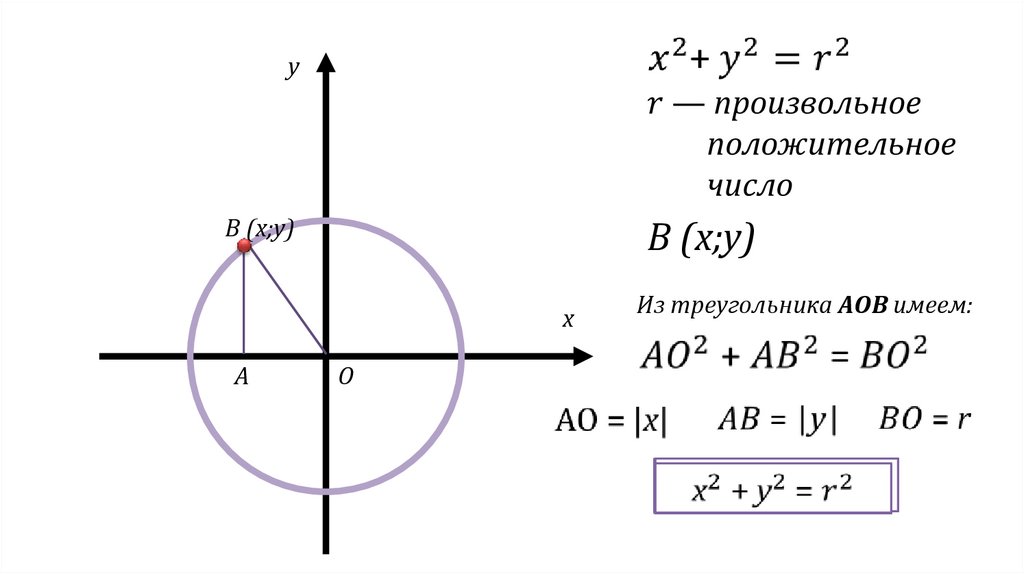
yB (x;y)
B (x;y)
x
A
O
Из треугольника АOB имеем:
12.
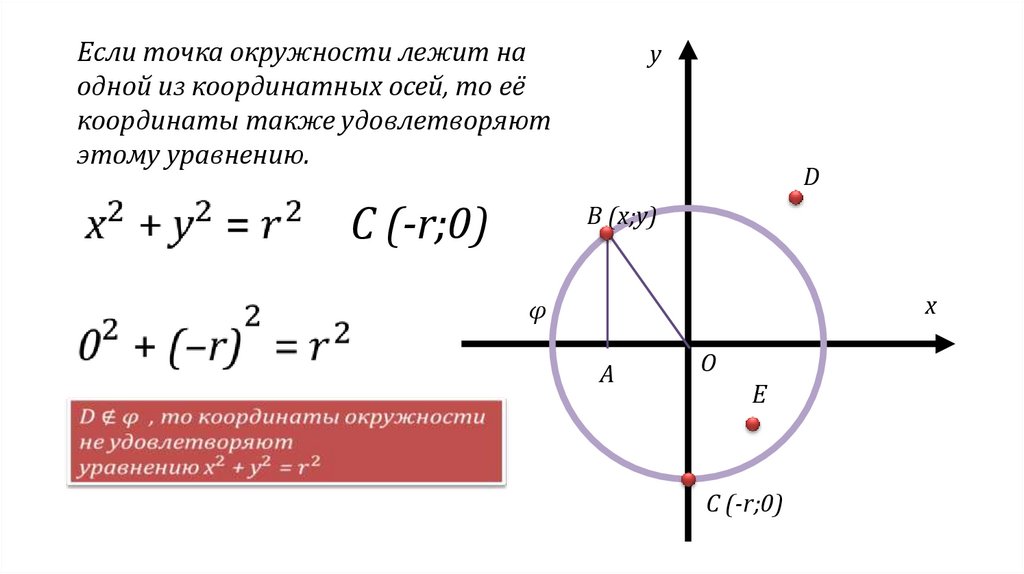
Eсли точка окружности лежит наодной из координатных осей, то её
координаты также удовлетворяют
этому уравнению.
С (-r;0)
y
D
B (x;y)
x
φ
A
O
E
С (-r;0)
13.
yφ
x
0
14.
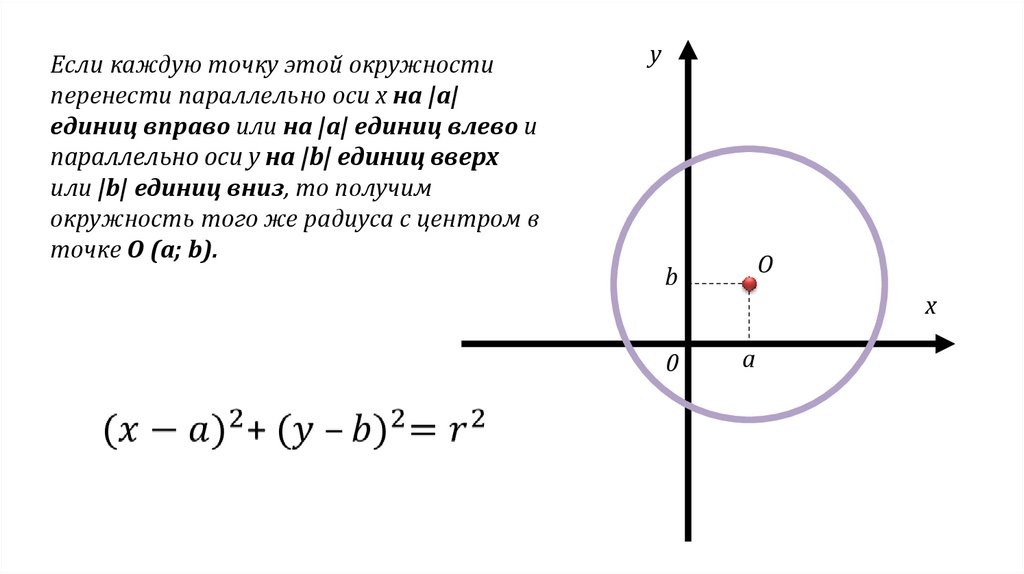
Если каждую точку этой окружностиперенести параллельно оси x на |а|
единиц вправо или на |а| единиц влево и
параллельно оси y на |b| единиц вверх
или |b| единиц вниз, то получим
окружность того же радиуса с центром в
точке О (а; b).
y
O
b
0
x
a









 mathematics
mathematics








