Матрицы и определители

1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ Программа подготовки бакалавров по направлению «Экономика»

Кафедра Экономики и управления
МАТРИЦЫ
И ОПРЕДЕЛИТЕЛИ
Программа подготовки бакалавров по направлению
«Экономика»
Хамидуллин Р.Я.
Заведующий кафедрой ВМ и ЕНД

2.

Определитель – это число,
которое вычисляется по формулам,
схемам и правилам.
Обозначается:
D
A
det A

3.

Определителем первого порядка матрицы
A (a11)
называется число
То есть:
A a11 a11
a11

4.

Определителем второго порядка
называется число, которое
определяется по правилу:
a11
a12
a21 a22
a11 a22 a12 a 21

5.

Определителем третьего порядка
называется число, которое
определяется по правилу:
a11 a12 a13
a21 a22 a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a31 a32 a33
a13 a22 a31 a12 a21 a33 a11 a23 a32

6.

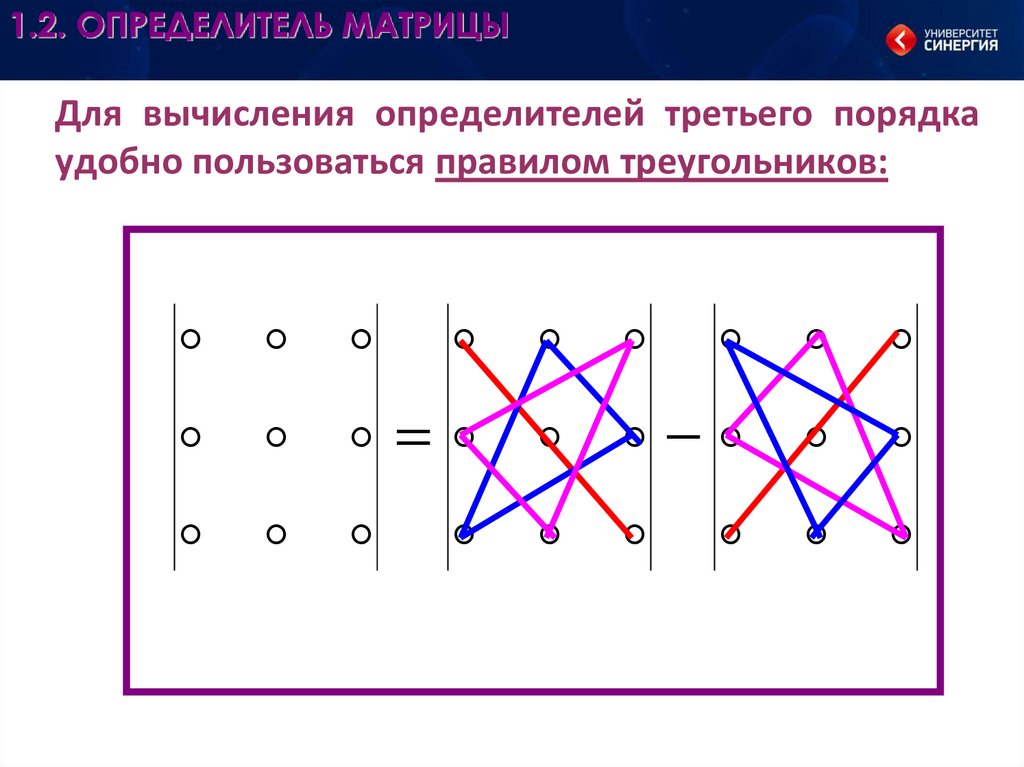
Для вычисления определителей третьего порядка
удобно пользоваться правилом треугольников:

7.

Вычислить определители матриц:
1 2
A
3 5
1 1 1
B 2 1 1
1 1 2

8.

A
1
2
3 5
1 5 ( 3) 2 11
1 1 1
B 2
1
1
1
1
2
1 1 2 ( 1) 1 1 1 2 1 1 1 1 ( 1) 2 2 1 1 1 5

9.

3 2 1
2 0 2
2 1 1
Минором M элемента a ijопределителя D
ij
называется такой новый определитель,
полученный из данного определителя
вычеркиванием строки и столбца,
на пересечении которых стоит
данный элемент.
Минор элемента определителя
обозначается как
M ij
a ij

10.

Алгебраическим дополнением
элемента аij определителя D
называется минор Mij этого элемента,
умноженный на (-1)s , где S=i+j- сумме
индексов i+j.
Обозначают: Aij
Aij ( 1) M ij
S
S i j

11.

В частности, минор элемента
a11
определителя третьего порядка найдется по
правилу:
a11
a12
a13
a21 a22
a23
a31
a33
a32
M 11
Его алгебраическое дополнение:
1 1
A11 ( 1) M11 M11
a22
a23
a32
a33

12.

1
Определитель транспонированной
матрицы равен определителю
исходной матрицы.
A A
T

13.

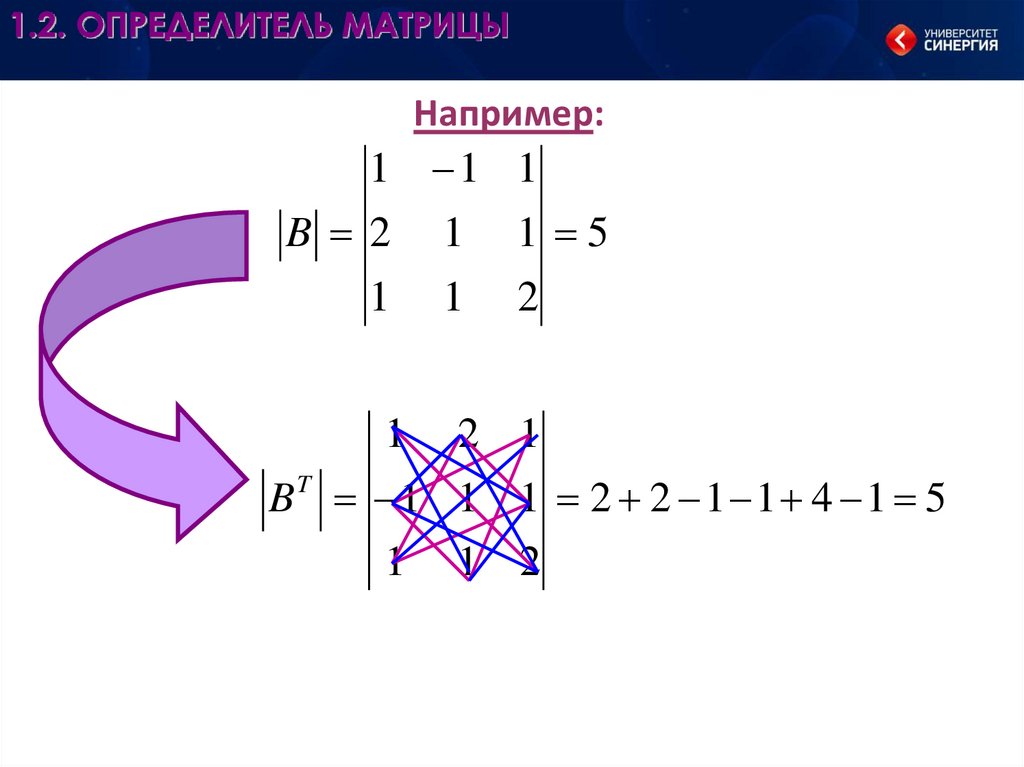
Например:
1 1 1
B 2
1
1 5
1
1
2
1
2 1
BT 1 1 1 2 2 1 1 4 1 5
1
1 2

14.

2
При перестановке двух строк
или столбцов определитель
изменит свой знак на
противоположный.

15.

Например:
1 1 1
B 2
1
1 5
1
1
2
Меняем местами первую и вторую строки:
2
1
1
1 1 1 4 1 1 1 2 2 5
1
1
2

16.

3
Если определитель имеет две
одинаковые строки или столбца,
то он равен нулю.

17.

Например:
1 1 3
2
2
2 4 4 12 12 4 4 0
2
2
2

18.

4
Общий множитель строки или
столбца можно выносить за знак
определителя.

19.

Например:
1 1 1
2
2
2 4 2 2 2 4 2 4
1
1
2
Выносим из второй строки множитель 2:
1 1 1
1 1 1
2
2 2 2 1 1
1 2 (2 1 1 1 2 1) 2 2 4
1
1 2
2
1 1

20.

5
Определитель не изменится, если
к элементам одной строки или столбца
прибавить соответственные элементы
другой строки или столбца,
умноженные на одно и то же число.

21.

Например:
1 1 1
B 2
1
1 5
1
1
2
Первую строку умножаем на 2 и складываем
со второй:
1 1 1
4 1 3 2 3 4 1 8 3 5
1
1
2

22.

6
Треугольный определитель, у которого
все элементы, лежащие выше (или ниже)
главной диагонали- нули, равен
произведению элементов
главной диагонали.

23.

Например:
= 3·3·3=27

24.

7
Определитель равен сумме
произведений элементов какойлибо строки или столбца на их
алгебраические дополнения:
n
A ai1 Ai1 ai 2 Ai 2 ... ain Ain aik Aik
k 1

25.

Вычислить определитель:
1
2
3
4
1
2
3
1
0
1
1
0
2
3
4
1

26.

Раскладываем определитель по третьей
строке:
1 2 3 4
1 2 3 1
0 1 1 0
0 A31 1 A32 1 A33 0 A34 A32 A33
2 3 4 1
Находим алгебраические дополнения:
=

27.

1 3 4
A32 ( 1) 3 2 M 32 1 3 1 (3 6 16 24 3 4) 6
2 4 1
1 2 4
A33 ( 1)
3 3
M 33 1 2 1 2 4 12 16 2 3 3
2 3 1
Подставляем полученный результат:
=
6 ( 3) 3

28.

Вывод:
Способы вычисления определителя.

29.

1
1. Определители второго и третьего
порядка вычисляют по схемам.

30.

2. Определитель можно вычислить
с помощью его разложения по элементам
строки или столбца (свойство 7).

31.

3
3. Определитель можно вычислить
способом приведения его
к треугольному виду.

32.

Этот способ основан на том, что
по свойству 6,
треугольный определитель равен
произведению элементов главной
диагонали.

33.

Чтобы получить треугольный
определитель, надо, по свойству 5
к какой-либо строке или столбцу
определителя

34.

прибавить соответствующие элементы
другой строки или столбца, умноженные
на одно и тоже число, до тех пор,
пока не придем к определителю
треугольного вида.

35.

Вычислить определитель:

36.

Практикум 2.1 Определители
1. Вычислить определители:
10 14
1 4
a)
; б)
;
6 21
3 2
1. 2. Вычислить определители третьего порядка разными способами(треугольников,
полосочками и по свойству 6)
1
2
5
2 3 4
a) 5 2 1 ; б) 3 4 7 ;
3 12 15
1 2 3
1. 3. Вычислить определители, используя разложение по 1 строке или 2-му столбцу,
свойства определителей:
0 5 2 0
2 1 3 1
8 3 5 4
1 1 2 4
; б)
;
a)
7 2 4 1
3 2 1 3
0 4 1 0
5 2 1 2

37.

Практикум 2.2 Определители
Вычислить
значение
определителя
различными
способами
(разложение по 2 строке, 2 столбцу и приведением к треугольному виду)
2 3 4 5
5
4
2
3
для матрицы A
.
4 5 3 2
3 2 5 4
1 2
2 5
3
7
1
4
2. Вычислить определитель матрицы: A
- любой
5 9
2 7
1 2
4 6
способ
3 1
3. Вычислить определители матриц (любой способ): а)
;
4
6
2 3 4 5
1 6 3
3
4
5
2
;
6
1
2
в)
б)
;
4 5 2 3
3
2 1
5 2 3 4
1.