Similar presentations:
Основы термодинамики
1. ОСНОВЫ ТЕРМОДИНАМИКИ
2.
Термодинамика – раздел физики вкотором
изучаются
макроскопические
системы и происходящие в них процессы с
энергетической точки зрения, не учитывая их
атомно-молекулярное строение.
В термодинамике рассматриваются две формы
передачи энергии системе:
энергия может быть передана в форме
теплоты и в форме работы.
3. Энергия, теплота, работа
Энергия– единая количественная мера
различных
форм
движения
материи
и
соответствующих им взаимодействий. Энергия
количественно характеризует систему с точки
зрения
возможных
в
ней
превращений
движения.
Энергией
система
обладает
всегда.
Энергия - однозначная функция состояния: в данном
состоянии она принимает одно вполне определённое
значение.
2
При переходе из одного
dWсостояния
W Wв2 другое
W1. происходит
изменение энергии: 1
4. Работа -
Работа процесс передачи энергии системе при воздействии на неёвнешних сил.
Работа совершается при изменении состояния системы.
В отличие от энергии работа – функция поцесса. Она
зависит от того, каким способом система переходит из
одного состояния в другое.
2
При переходе из состояния 1 в состояние 2:
А А12
Сравнить с энергией: А12 ≠ А2 – А1,
1
d – полный дифференциал; δ – неполный дифференциал.
5. Теплота -
Теплота это энергия, передаваемая системе в процессе теплообменас внешними телами.
Теплота, как и работа, - функция процесса.
При совершении над системой работы может меняться
как внутренняя энергия системы, так и её внешняя
механическая энергия.
При теплообмене изменяется только внутренняя энергия
системы.
При переходе системы в процессе 2 теплообмена из
состояния 1 в состояние 2:
Q Q12
1
6. Первый закон термодинамики
Изменение энергии системы происходит при сообщении ейтеплоты Q и совершении над системой работы А′ :
∆W = Q + A′
W – полная энергия системы. Она состоит из кинетической
энергии Wкмех механического движения системы как
целого, её потенциальной энергии Wпвнеш во внешнем
поле и внутренней энергии U. В термодинамике
рассматриваются процессы при которых Wкмех и Wпвнеш не
изменяются, поэтому эти виды энергии не рассматриваются.
Работа над системой A′ и работа самой системы A связаны:
A′ = - A
7.
С учётом этого:Q= ∆U + A
Теплота,
сообщаемая
системе,
расходуется на изменение внутренней
энергии системы и на совершение системой
работы против внешних сил.
В дифференциальной форме:
Q = dU + A
Q > 0 - теплота подводится к системе;
Q < 0 - теплота отводится от системы.
8. Другая формулировка 1 начала термодинамики
Невозможен вечный двигатель 1-ого рода, то естьдвигатель, который совершал бы работу в количестве
большем, чем полученная извне энергия (невозможен
к.п.д.>100%).
Q = ∆U + A
U dU 0 ,
Q=A
A не может быть > Q
9. Внутренняя энергия системы
В общем случае внутренняя энергия системы Uсостоит из :
а) кинетической энергии теплового движения молекул;
б) потенциальной энергии их взаимодействия;
в) внутриатомной энергии;
г) внутриядерной энергии.
В молекулярной физике энергии (в) и (г) не
учитываются. Для идеального газа энергия (б) не
учитывается.
10. Внутренняя энергия идеального газа состоит только из кинетической энергии теплового движения молекул.
Энергия одной молекулы с i степенями свободы<w>= i ( kT / 2)
Для произвольной массы газа m:
U = ν ΝА <w>
i m
i m
U = N A kT RT
2
2
i m
U
RT
2
или
i
U PV
2
11. Работа по изменению объёма газа
A>0 - система совершает работу надвнешними телами;
A<0 - над системой совершают работу
внешние силы.
2
A12 А
1
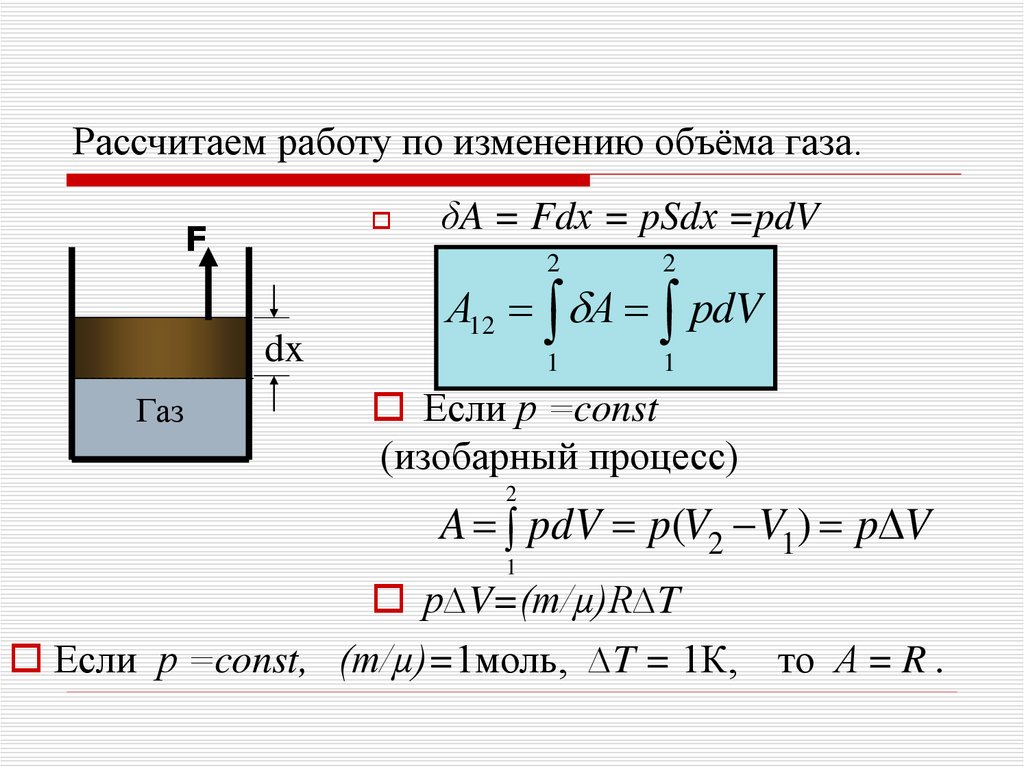
12. Рассчитаем работу по изменению объёма газа.
Fdx
Газ
δA = Fdх = pSdх =pdV
2
2
1
1
А12 А рdV
Если р =const
(изобарный процесс)
2
A pdV p(V2 V1) p V
1
р∆V=(m/µ)R∆T
Если р =const, (m/µ)=1моль, ∆T = 1К,
то А = R .
13. Основы теории теплоёмкости газов 1. Основные понятия
Теплоемкость газаС
Q
dT
Q
С
T
Удельная теплоемкость
Q
Q
с0
с0
m T
mdT
Молярная теплоемкость
Q
с
dT
с =µс0,
Q
с
T
[С]=Дж/К
[c0] = Дж/(кг.К)
[c] = Дж/(моль.К)
С с
14. 2. V = const, A=p∆V=0
Qv =cvν∆T ,c другой стороны:
Qv = ∆U = (i/2)νR∆T
Теплоемкость моля идеального газа
при
постоянном объеме
i равна :
CV
2
R
15. 3. p = const
Qp = cp ν ∆T,c другой стороны:
Qp= А + ∆U = p∆V+(i/2)νR∆T =
= νR∆T +(i/2)νR∆T = ( 1 + i/2)νR∆T
Молярная теплоёмкость при постоянном
давлении равна:
i 2
i
ср
R
с р (1 ) R или
2
2
ср = R + cv (уравнение Майера )
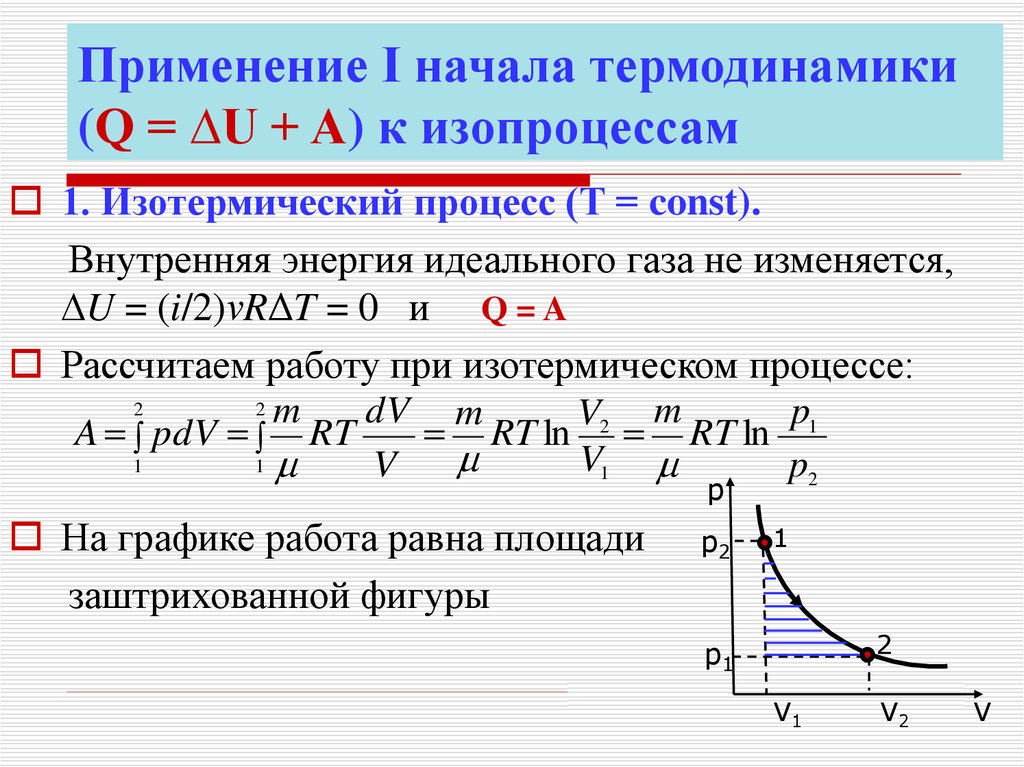
16. Применение Ι начала термодинамики (Q = ∆U + A) к изопроцессам
1. Изотермический процесс (Т = const).Внутренняя энергия идеального газа не изменяется,
U = (i/2)νRΔT = 0 и Q = A
Рассчитаем работу при изотермическом процессе:
2
2 m
dV m
p1
V2 m
A pdV RT
RT ln RT ln
V1
1
1
V
p2
p
На графике работа равна площади
заштрихованной фигуры
p2
1
2
p1
V1
V2
V
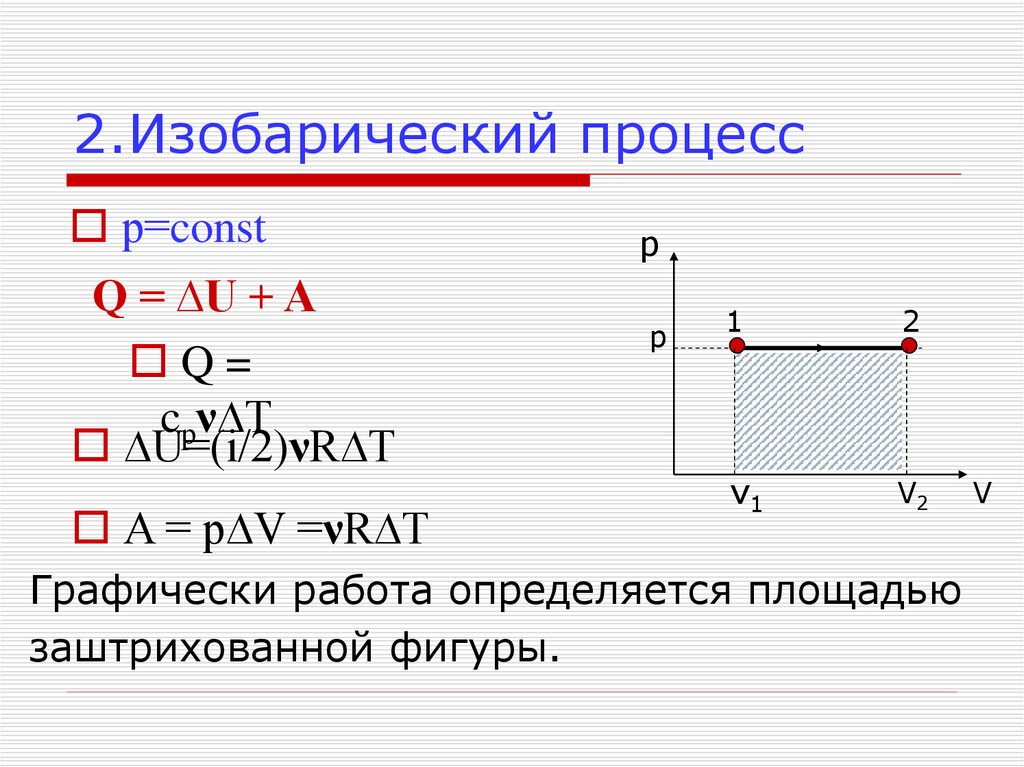
17. 2.Изобарический процесс
р=constQ = ∆U + A
Q=
cpν∆Т
∆U=(i/2)νR∆T
A = p∆V =νR∆T
p
p
1
2
v1
V2
Графически работа определяется площадью
заштрихованной фигуры.
V
18. 3. Изохорический процесс
V = constA = ∫pdV = 0
Q = ∆U
Q = ∆U = cvν∆T=
= (i/2)νR∆T
p
p1
1
p2
2
V
V
19. 4. Адиабатический процесс
Адиабатным(адиабатическим)
называется
процесс,
происходящий в термодинамической системе без теплообмена с
окружающими телами.
Необходимое и достаточное условие адиабатного процесса:
δQ = 0
I начало термодинамики для адиабатного процесса:
∆U = - A
Уравнение адиабатного процесса имеет вид:
p1V1 p2V2
или
γ = cр / cV = (i + 2) / i
pV const уравнение Пуассона
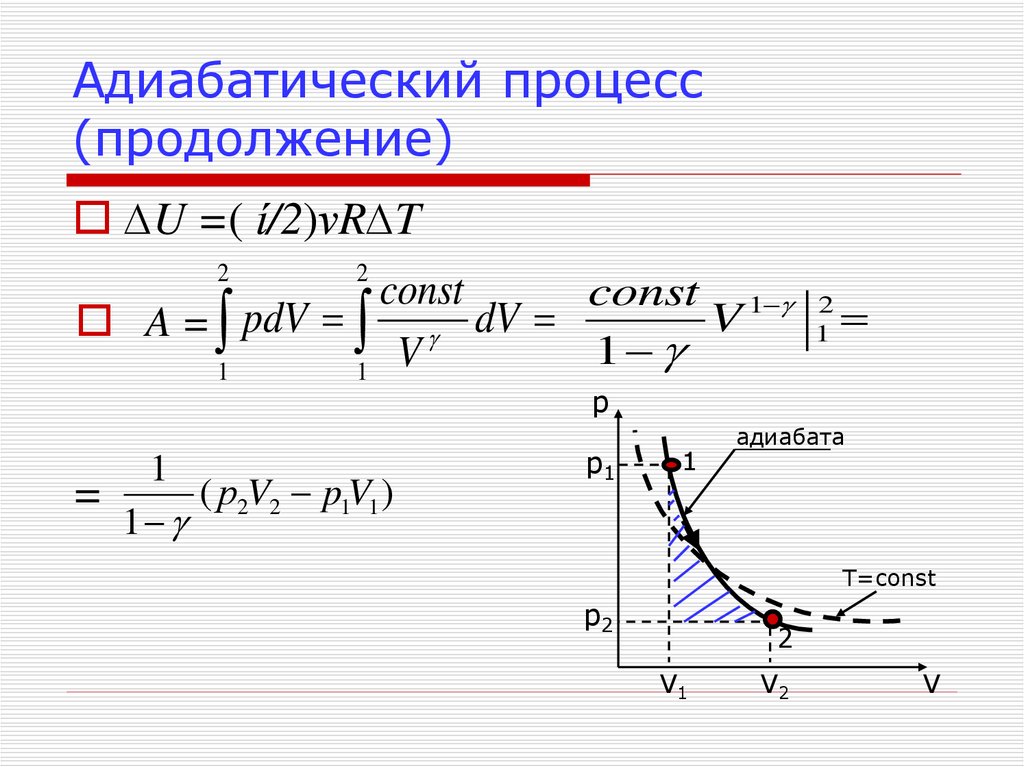
20. Адиабатический процесс (продолжение)
∆U =( ί/2)νR∆T2
2
const
const 1
V
A = pdV dV
1
V
1
1
2
1
р
=
1
( р2V2 p1V1 )
1
p1
1
адиабата
T=const
p2
2
V1
V2
V
21. Обратимые и необратимые процессы
Обратимыми называются процессы, которыепредполагают возможность возвращения системы в
исходное состояние без каких-либо изменений в
окружающей среде.
Необратимые процессы в одном направлении
протекают самопроизвольно, а для протекания в
обратном направлении требуют внешних затрат
(необходим «компенсирующий процесс»).
Все процессы, протекающие при конечных
разностях температур или при наличии сил трения,
являются необратимыми. Т.об., все реальные
процессы являются необратимыми.
22. Круговые процессы
Если тело из состояния 1 переводится в состояние 2, а затемчерез другие промежуточные состояния возвращается
в
состояние 1, то совершается круговой процесс или цикл.
р
p2
Прямой цикл
1
р
p2
1
Обратный цикл
b
a
a
b
2
p1
V1
V2 V
p1
2
V1
V2 V
А1а2>A 2в1,
А1а2<A 2в1,
А = А1а2-A 2в1 >0
А= А1а2-A 2в1 <0
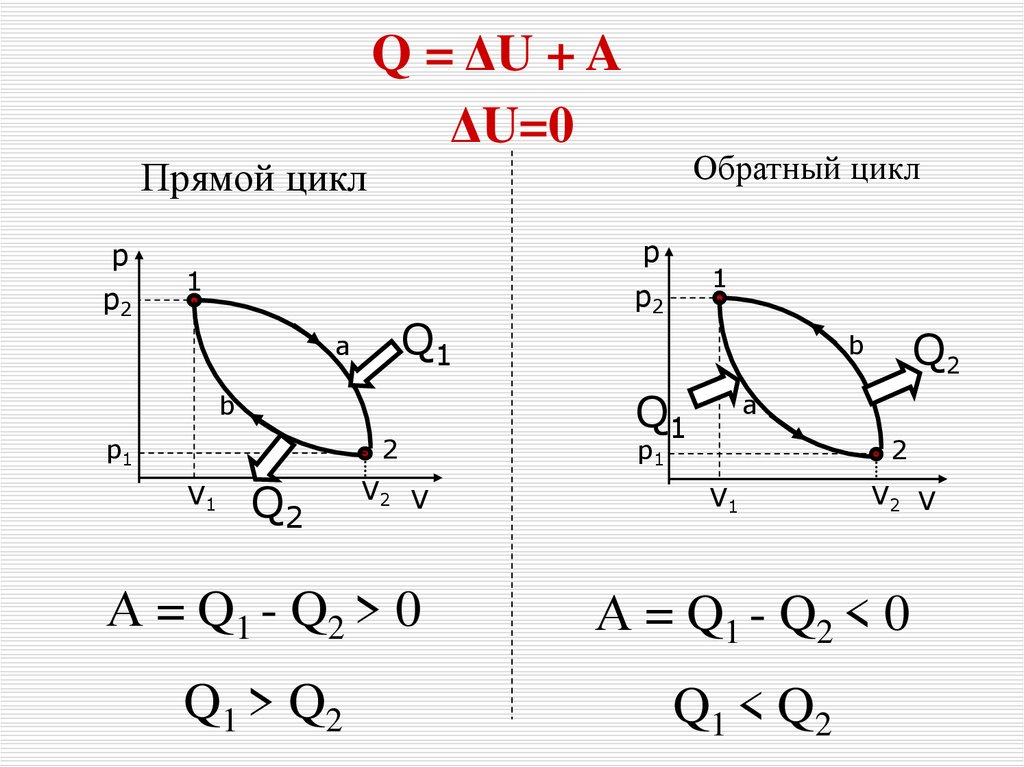
23.
Q = ΔU + AΔU=0
Обратный цикл
Прямой цикл
р
p2
р
1
Q1
a
b
2
p1
V1
Q2
V2 V
1
p2
Q2
b
Q1
a
p1
2
V1
V2 V
А = Q1 - Q2 > 0
А = Q1 - Q2 < 0
Q 1 > Q2
Q1 < Q 2
24. К.п.д. тепловой машины
К.п.д. тепловой машины ( ) - этоотношение совершаемой за цикл работы
А к получаемой за цикл теплоте Q1.
A
Q1
Q1 Q 2
Q1
1
Q2
Q1
25. Второе начало термодинамики
Клаузиус: не возможен процесс,единственным результатом которого был
бы переход теплоты от холодного тела к
нагретому.
Томсон: Невозможен такой периодический
процесс, единственным результатом
которого было бы получение работы за
счёт теплоты, взятой от одного источника.
26. Второе начало термодинамики (продолжение)
Невозможен вечный двигательвторого рода (перпетуум мобиле
второго рода ), т.е. двигатель,
полностью
превращающий
в
работу всю полученную извне
теплоту (имеющий к.п.д. 100 %).
27. Цикл Карно
Сади Карно установил, что наибольший к.п.д.имеет процесс, состоящий из двух изотерм и
двух адиабат.
1
2 Т1=const
2
3 δQ=0
Q1
3
4 Т2=const
4
1 δQ=0
Q2
28. Цикл Карно (продолжение)
К.п.д. цикла КарноQ1 Q2 А12 А 34
Q1
А12
V2
A RT ln
V1
m
T
T
1 T 2
2
1
T1
T1
Q1
Q
V2 V3
V1 V4
2
T
T
1 T 2
2
необ
1
T1
T1
29.
TT
1 T 2
2
1
T1
T1
-
одна из математических формулировок II начала
термодинамики, или:
Q1 Q2 T 1 T 2
Q1
T1
30. Приведенное количество теплоты
Отношение количества теплоты Q, полученной илиотданной системой (телом) при изотермическом
процессе к температуре Т этого процесса называется
приведенным количеством теплоты:
Q
Q
T
Для произвольного процесса
Q
dQ
T
При нагревании тела
при охлаждении
Q
Q 0
Q
T
Q 0
31.
Для обратимого цикла КарноQ
0, так как
Q
T
Q1 Q2
0
Q
T1 T 2
Интеграл
некоторой
Q
выражает изменение
T
функции состояния тела,
названной Клаузиусом энтропией тела и
обозначаемой S.
32. Энтропия – функция состояния системы
Изменение энтропииdS
Q
T
При переходе системы из состояния 1 в
2
Q
S2 S1
состояние 2:
1 T
Энтропия системы тел равна сумме энтропий
тел, входящих в систему
Энтропия изолированной системы при любых
происходящих в ней процессах не может убывать:
S 0
ещё одна математическая
dS ≥ 0
формулировка II начала термодинамики
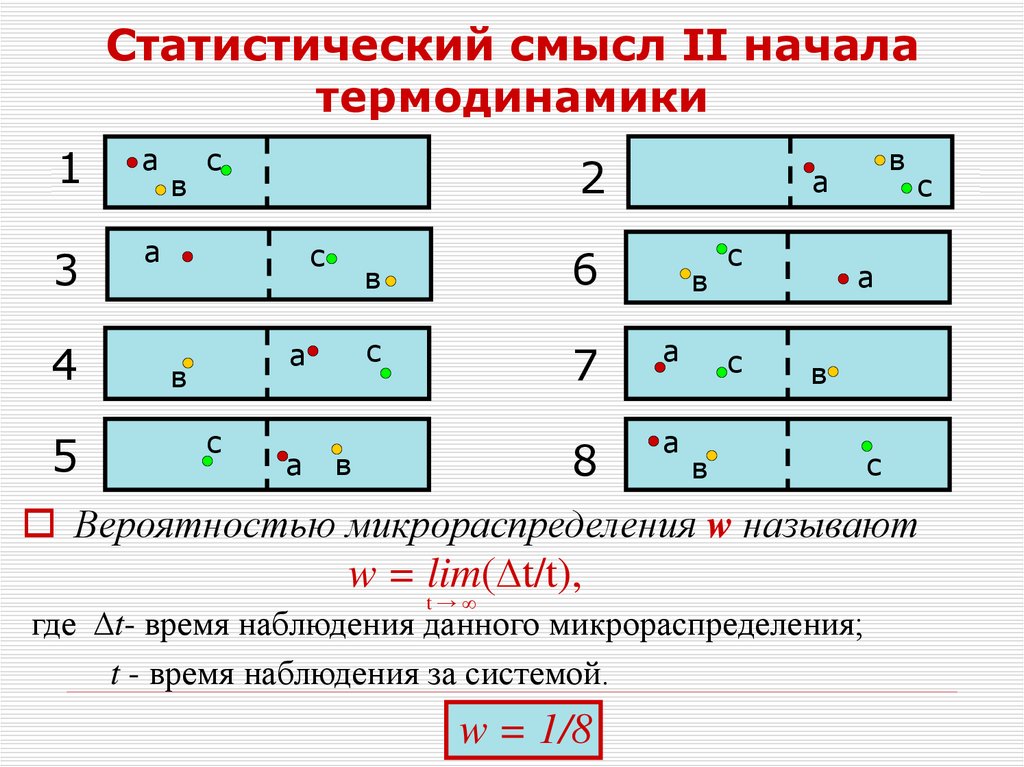
33. Статистический смысл II начала термодинамики
1а
3
а
4
5
в
с
2
с
с
а
в
с
а
6
в
в
в
а
в
7
а
8
а
с
с
с
а
в
в
с
Вероятностью микрораспределения w называют
w = lim(∆t/t),
t→∞
где ∆t- время наблюдения данного микрораспределения;
t - время наблюдения за системой.
w = 1/8
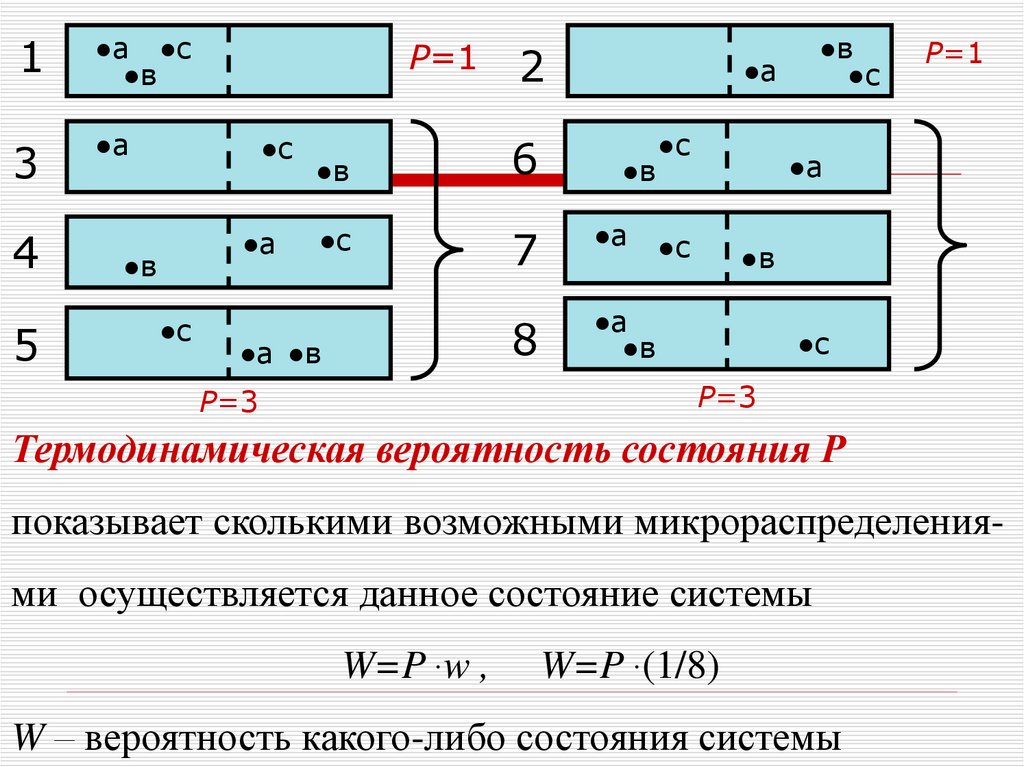
34.
1●а ●с
●в
3
●а
4
5
Р=1
●с
●а
●в
●с
2
●а
●в
6
●с
7
●а
8
●а
●в
●а ●в
●в
●с
●в
●с
Р=1
●а
●с
●в
●с
Р=3
Р=3
Термодинамическая вероятность состояния Р
показывает сколькими возможными микрораспределения-
ми осуществляется данное состояние системы
W=P w ,
W=P (1/8)
W – вероятность какого-либо состояния системы
35.
Больцман постулировал, что междуэнтропией и термодинамической вероятностью
существует связь:
S = k lnР
где k –постоянная Больцмана,
Р - термодинамическая вероятность.
Для замкнутой системы W~P, поэтому:
S ~ k lnW
Для любых процессов в замкнутой системе:
ΔW > 0, следовательно и ΔS > 0.
36. Статистический смысл второго начала термодинамики
Закон возрастания энтропии выражает постояннуютенденцию системы к переходу в более вероятное
состояние.
Чем из меньшего числа частиц состоит система, тем
более вероятны отступления от второго начала
термодинамики (флуктуации).
Процессы, невозможные по второму закону, в
статистической физике являются не невозможными,
а только очень мало вероятными.
37. Границы применимости II начала термодинамики
II начало термодинамики выполняетсятем более точно, чем из большего числа
частиц состоит система;
II начало термодинамики применимо для
замкнутых систем.






























 physics
physics








